Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Guśpiel, Grzegorz
Micek, Piotr
and
Polak, Adam
2018.
On an Extremal Problem for Poset Dimension.
Order,
Vol. 35,
Issue. 3,
p.
489.
Nagy, Dániel T.
2018.
Forbidden subposet problems with size restrictions.
Journal of Combinatorial Theory, Series A,
Vol. 155,
Issue. ,
p.
42.
Tomon, István
2019.
Forbidden induced subposets of given height.
Journal of Combinatorial Theory, Series A,
Vol. 161,
Issue. ,
p.
537.
Gerbner, Dániel
Methuku, Abhishek
Nagy, Dániel T.
Patkós, Balázs
and
Vizer, Máté
2019.
Forbidding Rank-Preserving Copies of a Poset.
Order,
Vol. 36,
Issue. 3,
p.
611.
Gunby, Benjamin
and
Pálvölgyi, Dömötör
2019.
Asymptotics of pattern avoidance in the Klazar set partition and permutation-tuple settings.
European Journal of Combinatorics,
Vol. 82,
Issue. ,
p.
102992.
Frankl, Peter
and
Kupavskii, Andrey
2019.
Partition‐free families of sets.
Proceedings of the London Mathematical Society,
Vol. 119,
Issue. 2,
p.
440.
Tomon, István
2020.
Packing the Boolean lattice with copies of a poset.
Journal of the London Mathematical Society,
Vol. 101,
Issue. 2,
p.
589.
Keszegh, Balázs
Lemons, Nathan
Martin, Ryan R.
Pálvölgyi, Dömötör
and
Patkós, Balázs
2021.
Induced and non-induced poset saturation problems.
Journal of Combinatorial Theory, Series A,
Vol. 184,
Issue. ,
p.
105497.
Gerbner, Dániel
Nagy, Dániel T.
Patkós, Balázs
and
Vizer, Máté
2022.
Forbidden subposet problems in the grid.
Discrete Mathematics,
Vol. 345,
Issue. 3,
p.
112720.
Sudakov, Benny
Tomon, István
and
Wagner, Adam Zsolt
2022.
Uniform chain decompositions and applications.
Random Structures & Algorithms,
Vol. 60,
Issue. 2,
p.
261.
Axenovich, Maria
and
Winter, Christian
2023.
Poset Ramsey numbers: large Boolean lattice versus a fixed poset.
Combinatorics, Probability and Computing,
p.
1.
Axenovich, Maria
and
Winter, Christian
2024.
Poset Ramsey Number $$R(P,Q_n)$$. II. N-Shaped Poset.
Order,
Vol. 41,
Issue. 2,
p.
401.
Winter, Christian
2024.
Poset Ramsey number R(P,Q). III. Chain compositions and antichains.
Discrete Mathematics,
Vol. 347,
Issue. 7,
p.
114031.
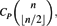 $$C_P{\binom{n}{\lfloor\gfrac{n}{2}\rfloor}},$$
$$C_P{\binom{n}{\lfloor\gfrac{n}{2}\rfloor}},$$