Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T22:58:30.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Expanders Are Universal for the Class of All Spanning Trees

Published online by Cambridge University Press:  03 January 2013

DANIEL JOHANNSEN ,
MICHAEL KRIVELEVICH  and
WOJCIECH SAMOTIJ
DANIEL JOHANNSEN
Affiliation:
School of Mathematical Sciences, Tel Aviv University, Tel Aviv, 69978, Israel (e-mail: [email protected], [email protected])
MICHAEL KRIVELEVICH
Affiliation:
School of Mathematical Sciences, Tel Aviv University, Tel Aviv, 69978, Israel (e-mail: [email protected], [email protected])
WOJCIECH SAMOTIJ
Affiliation:
School of Mathematical Sciences, Tel Aviv University, Tel Aviv, 69978, Israel (e-mail: [email protected], [email protected]) Trinity College, Cambridge CB2 1TQ, UK (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

A graph is called universal for a given graph class 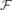(or, equivalently, 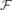-universal) if it contains a copy of every graph in 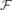as a subgraph. The construction of sparse universal graphs for various classes 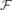has received a considerable amount of attention. There is particular interest in tight 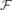-universal graphs, that is, graphs whose number of vertices is equal to the largest number of vertices in a graph from 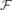. Arguably, the most studied case is that when 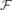is some class of trees. In this work, we are interested in (n,Δ), the class of all n-vertex trees with maximum degree at most Δ. We show that every n-vertex graph satisfying certain natural expansion properties is (n,Δ)-universal. Our methods also apply to the case when Δ is some function of n. Since random graphs are known to be good expanders, our result implies, in particular, that there exists a positive constant c such that the random graph G(n,cn−1/3log2n) is asymptotically almost surely (a.a.s.) universal for (n,O(1)). Moreover, a corresponding result holds for the random regular graph of degree cn2/3log2n. Another interesting consequence is the existence of locally sparse n-vertex (n,Δ)-universal graphs. For example, we show that one can (randomly) construct n-vertex (n,O(1))-universal graphs with clique number at most five. This complements the construction of Bhatt, Chung, Leighton and Rosenberg (1989), whose (n,Δ)-universal graphs with merely O(n) edges contain large cliques of size Ω(Δ). Finally, we show that random graphs are robustly (n,Δ)-universal in the context of the Maker–Breaker tree-universality game.

Keywords

Primary 05C35Secondary 05C0505C8005D40
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 22 , Issue 2 , March 2013 , pp. 253 - 281
Copyright
Copyright © Cambridge University Press 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Ajtai, M., Komlós, J. and Szemerédi, E. (1981) The longest path in a random graph. Combinatorica 1 1–12.CrossRefGoogle Scholar
[2]Alon, N. and Asodi, V. (2002) Sparse universal graphs. J. Comput. Appl. Math. 142 1–11.CrossRefGoogle Scholar
[3]Alon, N. and Capalbo, M. (2007) Sparse universal graphs for bounded-degree graphs. Random Struct. Alg. 31 123–133.CrossRefGoogle Scholar
[4]Alon, N., Capalbo, M., Kohayakawa, Y., Rödl, V., Ruciński, A. and Szemerédi, E. (2000) Universality and tolerance. In FOCS '00: Proc. 41st Annual IEEE Syposium on Foundations of Computer Science, IEEE, pp. 14–21.CrossRefGoogle Scholar
[5]Alon, N., Krivelevich, M. and Sudakov, B. (2007) Embedding nearly-spanning bounded degree trees. Combinatorica 27 629–644.CrossRefGoogle Scholar
[6]Babai, L., Chung, F. R. K., Erdős, P., Graham, R. L. and Spencer, J. H. (1982) On graphs which contain all sparse graphs. Ann. Discrete Math. 12 21–26.Google Scholar
[7]Balogh, J., Csaba, B., Pei, M. and Samotij, W. (2010) Large bounded degree trees in expanding graphs. Electron. J. Combin. 17 R6.CrossRefGoogle Scholar
[8]Balogh, J., Csaba, B. and Samotij, W. (2011) Local resilience of almost spanning trees in random graphs. Random Struct. Alg. 38 121–139.CrossRefGoogle Scholar
[9]Beck, J. (1982) Remarks on positional games I. Acta Math. Hungar. 40 65–71.CrossRefGoogle Scholar
[10]Beck, J. (2008) Combinatorial Games: Tic-Tac-Toe Theory, first edition, Vol. 114 of Encyclopedia of Mathematics and its Applications, Cambridge University Press.Google Scholar
[11]Bender, E. A. and Wormald, N. C. (1988) Random trees in random graphs. Proc. Amer. Math. Soc. 103 314–320.CrossRefGoogle Scholar
[12]Bhatt, S. N., Chung, F. R. K., Leighton, F. T. and Rosenberg, A. L. (1989) Universal graphs for bounded-degree trees and planar graphs. SIAM J. Discrete Math. 2 145–155.CrossRefGoogle Scholar
[13]Bollobás, B. (1984) The evolution of sparse graphs. In Graph Theory and Combinatorics, Academic Press, pp. 35–57.Google Scholar
[14]Böttcher, J., Taraz, A. and Würfl, A. (2011) Private communication.Google Scholar
[15]Capalbo, M. (2010) Explicit sparse almost-universal graphs for (n,k/n). Random Struct. Alg. 37 437–454.CrossRefGoogle Scholar
[16]Capalbo, M. R. and Kosaraju, S. R. (1999) Small universal graphs. In STOC '99: Proc. 31st Annual ACM Symposium on Theory of Computing, ACM, pp. 741–749.CrossRefGoogle Scholar
[17]Chung, F. R. K. and Graham, R. L. (1978) On graphs which contain all small trees. J. Combin. Theory Ser. B 24 14–23.CrossRefGoogle Scholar
[18]Chung, F. R. K. and Graham, R. L. (1979) On universal graphs. In Proc. 2nd International Conference on Combinatorial Mathematics, New York Academy of Sciences, pp. 136–140.Google Scholar
[19]Chung, F. R. K. and Graham, R. L. (1983) On universal graphs for spanning trees. J. London Math. Soc. (2) 27 203–211.CrossRefGoogle Scholar
[20]Chung, F. R. K., Graham, R. L. and Pippenger, N. (1978) On graphs which contain all small trees II. In Proc. 5th Hungarian Colloquium on Combinatorics, North-Holland, pp. 213–223.Google Scholar
[21]Dellamonica, D. Jr., Kohayakawa, Y., Rödl, V. and Ruciński, A. (2012) An improved upper bound on the density of universal random graphs. In LATIN '12: Proc. 10th Latin American International Conference on Theoretical Informatics, Springer, pp. 231–242.Google Scholar
[22]Dellamonica, D. Jr., Kohayakawa, Y., Rödl, V. and Ruciński, A. (2012) Universality of random graphs. SIAM J. Discrete Math. 26 353–374.CrossRefGoogle Scholar
[23]Elias, P., Feinstein, A. and Shannon, C. E. (1956) A note on maximum flow through a network. IRE Trans. Inform. Theory 2 117–119.CrossRefGoogle Scholar
[24]Erdős, P. and Selfridge, J. L. (1973) On a combinatorial game. J. Combin. Theory Ser. A 14 298–301.CrossRefGoogle Scholar
[25]Fernandez de la Vega, W. (1988) Trees in sparse random graphs. J. Combin. Theory Ser. B 45 77–85.CrossRefGoogle Scholar
[26]Ford, L. R. and Fulkerson, D. R. (1956) Maximal flow through a network. Canad. J. Math. 8 399–404.CrossRefGoogle Scholar
[27]Friedman, J. and Pippenger, N. (1987) Expanding graphs contain all small trees. Combinatorica 7 71–76.CrossRefGoogle Scholar
[28]Frieze, A. and Krivelevich, M. (2002) Hamilton cycles in random subgraphs of pseudo-random graphs. Discrete Math. 256 137–150.CrossRefGoogle Scholar
[29]Frieze, A. and Krivelevich, M. (2006) Almost universal graphs. Random Struct. Alg. 28 499–510.CrossRefGoogle Scholar
[30]Haxell, P. E. (2001) Tree embeddings. J. Graph Theory 36 121–130.3.0.CO;2-U>CrossRefGoogle Scholar
[31]Hefetz, D., Krivelevich, M. and Szabó, T. (2009) Hamilton cycles in highly connected and expanding graphs. Combinatorica 29 547–568.CrossRefGoogle Scholar
[32]Hefetz, D., Krivelevich, M. and Szabó, T. (2012) Sharp threshold for the appearance of certain spanning trees in random graphs. Random Struct. Alg. 41, 391–412.CrossRefGoogle Scholar
[33]Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, first edition, Interscience Series in Discrete Mathematics and Optimization, Wiley.CrossRefGoogle Scholar
[34]Komlós, J., Sárközy, G. N. and Szemerédi, E. (2001) Spanning trees in dense graphs. Combin. Probab. Comput. 10 397–416.CrossRefGoogle Scholar
[35]Komlós, J. and Szemerédi, E. (1983) Limit distribution for the existence of Hamiltonian cycles in a random graph. Discrete Math. 43 55–63.CrossRefGoogle Scholar
[36]Krivelevich, M. (1995) Bounding Ramsey numbers through large deviation inequalities. Random Struct. Alg. 7 145–156.CrossRefGoogle Scholar
[37]Krivelevich, M. (2010) Embedding spanning trees in random graphs. SIAM J. Discrete Math. 24 1495–1500.CrossRefGoogle Scholar
[38]Krivelevich, M. and Sudakov, B. (2002) Sparse pseudo-random graphs are Hamiltonian. J. Graph Theory 42 17–33.CrossRefGoogle Scholar
[39]Krivelevich, M. and Sudakov, B. (2006) Pseudo-random graphs. In More Sets, Graphs and Numbers, Vol. 15 of Bolyai Society Mathematical Studies, Springer, pp. 199–262.CrossRefGoogle Scholar
[40]Krivelevich, M., Sudakov, B., Vu, V. H. and Wormald, N. C. (2001) Random regular graphs of high degree. Random Struct. Alg. 18 346–363.CrossRefGoogle Scholar
[41]McKay, B. D. and Wormald, N. C. (1990) Uniform generation of random regular graphs of moderate degree. J. Algorithms 11 52–67.CrossRefGoogle Scholar
[42]Moon, J. W. (1968) On the maximum degree in a random graph. Michigan Math. J. 15 429–432.CrossRefGoogle Scholar
[43]Rödl, V. (1981) A note on universal graphs. Ars Combinatoria 11 225–229.Google Scholar
[44]Sudakov, B. and Vondrák, J. (2010) A randomized embedding algorithm for trees. Combinatorica 30 445–470.CrossRefGoogle Scholar