Article contents
Edge-statistics on large graphs
Published online by Cambridge University Press: 14 November 2019
Abstract
The inducibility of a graph H measures the maximum number of induced copies of H a large graph G can have. Generalizing this notion, we study how many induced subgraphs of fixed order k and size ℓ a large graph G on n vertices can have. Clearly, this number is 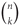 $\left( {\matrix{n \cr k}}\right)$ for every n, k and
$\left( {\matrix{n \cr k}}\right)$ for every n, k and 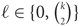 $\ell \in \left\{ {0,\left( {\matrix{k \cr 2}} \right)}\right\}$. We conjecture that for every n, k and
$\ell \in \left\{ {0,\left( {\matrix{k \cr 2}} \right)}\right\}$. We conjecture that for every n, k and 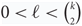 $0 \lt \ell \lt \left( {\matrix{k \cr 2}}\right)$ this number is at most
$0 \lt \ell \lt \left( {\matrix{k \cr 2}}\right)$ this number is at most 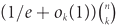 $ (1/e + {o_k}(1)) {\left( {\matrix{n \cr k}} \right)}$. If true, this would be tight for ℓ ∈ {1, k − 1}.
$ (1/e + {o_k}(1)) {\left( {\matrix{n \cr k}} \right)}$. If true, this would be tight for ℓ ∈ {1, k − 1}.
In support of our ‘Edge-statistics Conjecture’, we prove that the corresponding density is bounded away from 1 by an absolute constant. Furthermore, for various ranges of the values of ℓ we establish stronger bounds. In particular, we prove that for ‘almost all’ pairs (k, ℓ) only a polynomially small fraction of the k-subsets of V(G) have exactly ℓ edges, and prove an upper bound of 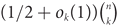 $ (1/2 + {o_k}(1)){\left( {\matrix{n \cr k}}\right)}$ for ℓ = 1.
$ (1/2 + {o_k}(1)){\left( {\matrix{n \cr k}}\right)}$ for ℓ = 1.
Our proof methods involve probabilistic tools, such as anti-concentration results relying on fourth moment estimates and Brun’s sieve, as well as graph-theoretic and combinatorial arguments such as Zykov’s symmetrization, Sperner’s theorem and various counting techniques.
- Type
- Paper
- Information
- Copyright
- © Cambridge University Press 2019
Footnotes
Research supported in part by NSF grant DMS-1855464, ISF grant 281/17, BSF grant 2018267 and the Simons Foundation.
The research of Dan Hefetz is supported by ISF grant 822/18.
Partially supported by USA-Israel BSF grants 2014361 and 2018267, and by ISF grant 1261/17.
The research of Mykhaylo Tyomkyn is supported in part by ERC Starting Grant 633509.
References
- 7
- Cited by


