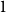1. Introduction
1.1 Simply generated trees
Simply generated trees were introduced by Meir and Moon [Reference Meir and Moon22], and owing to their use in describing an entire class of trees, have created a general framework for studying random trees. A simply generated family of rooted trees is characterised by a sequence of weights associated with the different possible outdegrees of a vertex. Specifically, for a given sequence of nonnegative real numbers
![]() $w_j$
(
$w_j$
(
![]() $j \geq 0$
), one defines the weight of a rooted ordered tree to be the product
$j \geq 0$
), one defines the weight of a rooted ordered tree to be the product
![]() $\prod _v w_{d(v)}$
over all vertices of the tree, where
$\prod _v w_{d(v)}$
over all vertices of the tree, where
![]() $d(v)$
denotes the outdegree (number of children) of
$d(v)$
denotes the outdegree (number of children) of
![]() $v$
. Letting
$v$
. Letting
![]() $\Phi (t) = \sum _{j \geq 0} w_j t^j$
be the weight generating function and
$\Phi (t) = \sum _{j \geq 0} w_j t^j$
be the weight generating function and
![]() $Y(x)$
the generating function in which the coefficient of
$Y(x)$
the generating function in which the coefficient of
![]() $x^n$
is the sum of the weights over all
$x^n$
is the sum of the weights over all
![]() $n$
-vertex rooted ordered trees, one has the fundamental relation
$n$
-vertex rooted ordered trees, one has the fundamental relation
Common examples of simply generated trees are: plane trees with weight generating function
![]() $\Phi (t) = 1/(1-t)$
; binary trees (
$\Phi (t) = 1/(1-t)$
; binary trees (
![]() $\Phi (t) = 1+t^2$
); pruned binary trees (
$\Phi (t) = 1+t^2$
); pruned binary trees (
![]() $\Phi (t) = (1+t)^2$
); and labelled trees (
$\Phi (t) = (1+t)^2$
); and labelled trees (
![]() $\Phi (t) = e^t$
). In the first three examples,
$\Phi (t) = e^t$
). In the first three examples,
![]() $Y(x)$
becomes an ordinary generating function with the total weight being the number of trees in the respective family, while
$Y(x)$
becomes an ordinary generating function with the total weight being the number of trees in the respective family, while
![]() $Y(x)$
can be seen as an exponential generating function in the case of labelled trees.
$Y(x)$
can be seen as an exponential generating function in the case of labelled trees.
In addition to the fact that the notion of simply generated trees covers many important examples, there is also a strong connection to the probabilistic model of Bienaymé–Galton–Watson trees: here, one fixes a probability distribution on the set of nonnegative integers. Next, a random tree is constructed by starting with a root that produces offspring according to the given distribution. In each subsequent step, all vertices of the current generation also produce offspring according to the same distribution, all independent of each other and independent of all previous generations. The process stops if none of the vertices of a generation have children. If the weights in the construction of a simply generated family are taken to be the corresponding probabilities of the offspring distribution, then one verifies easily that the distribution of a random
![]() $n$
-vertex tree from that family (with probabilities proportional to the weights) is the same as that of the Bienaymé–Galton–Watson process, conditioned on the event that the final tree has
$n$
-vertex tree from that family (with probabilities proportional to the weights) is the same as that of the Bienaymé–Galton–Watson process, conditioned on the event that the final tree has
![]() $n$
vertices.
$n$
vertices.
Conversely, even if the weight sequence of a simply generated family does not represent a probability measure, it is often possible to determine an equivalent probability measure that produces the same random tree distribution. For example, random plane trees correspond to a geometric distribution while random rooted labelled trees correspond to a Poisson distribution. We refer to [Reference Drmota8] and [Reference Janson17] for more background on simply generated trees and Bienaymé–Galton–Watson trees.
1.2 Protection numbers in trees
Protection numbers in trees measure the distance to the nearest leaf successor. Formally, this can be expressed as follows.
Definition 1.1 (Protection number). The protection number of a vertex
![]() $v$
is the length of the shortest path from
$v$
is the length of the shortest path from
![]() $v$
to any leaf contained in the maximal subtree where
$v$
to any leaf contained in the maximal subtree where
![]() $v$
is the root.
$v$
is the root.
Alternatively, the protection number can be defined recursively: a leaf has protection number
![]() $0$
, the parent of a leaf has protection number
$0$
, the parent of a leaf has protection number
![]() $1$
, and generally the protection number of an interior vertex is the minimum of the protection numbers of its children plus
$1$
, and generally the protection number of an interior vertex is the minimum of the protection numbers of its children plus
![]() $1$
. In this paper, we will be particularly interested in the maximum protection number of a tree, which is the largest protection number among all vertices. Fig. 1 shows an example of a tree along with the protection numbers of all its vertices.
$1$
. In this paper, we will be particularly interested in the maximum protection number of a tree, which is the largest protection number among all vertices. Fig. 1 shows an example of a tree along with the protection numbers of all its vertices.

Figure 1. A plane tree with 15 vertices and the protection number of each vertex indicated. The maximum protection number of this tree is
![]() $2$
.
$2$
.
The study of protection numbers in trees began with Cheon and Shapiro [Reference Cheon and Shapiro4] considering the average number of vertices with protection number of at least 2 (called
![]() $2$
-protected) in ordered trees. Several other authors contributed to knowledge in this direction, by studying the number of
$2$
-protected) in ordered trees. Several other authors contributed to knowledge in this direction, by studying the number of
![]() $2$
-protected vertices in various types of trees:
$2$
-protected vertices in various types of trees:
![]() $k$
-ary trees [Reference Mansour21]; digital search trees [Reference Du and Prodinger9]; binary search trees [Reference Mahmoud and Ward20]; ternary search trees [Reference Holmgren and Janson15]; tries and suffix trees [Reference Gaither, Homma, Sellke and Ward11]; random recursive trees [Reference Mahmoud and Ward19]; and general simply generated trees from which some previously known cases were also obtained [Reference Devroye and Janson7].
$k$
-ary trees [Reference Mansour21]; digital search trees [Reference Du and Prodinger9]; binary search trees [Reference Mahmoud and Ward20]; ternary search trees [Reference Holmgren and Janson15]; tries and suffix trees [Reference Gaither, Homma, Sellke and Ward11]; random recursive trees [Reference Mahmoud and Ward19]; and general simply generated trees from which some previously known cases were also obtained [Reference Devroye and Janson7].
Generalising the concept of a vertex being
![]() $2$
-protected,
$2$
-protected,
![]() $k$
-protected vertices – when a vertex has protection number at least
$k$
-protected vertices – when a vertex has protection number at least
![]() $k$
– also became a recent topic of interest. Devroye and Janson [Reference Devroye and Janson7] proved convergence of the probability that a random vertex in a random simply generated tree has protection number
$k$
– also became a recent topic of interest. Devroye and Janson [Reference Devroye and Janson7] proved convergence of the probability that a random vertex in a random simply generated tree has protection number
![]() $k$
. Copenhaver gave a closed formula for the number of
$k$
. Copenhaver gave a closed formula for the number of
![]() $k$
-protected vertices in all unlabelled rooted plane trees on
$k$
-protected vertices in all unlabelled rooted plane trees on
![]() $n$
vertices along with expected values [Reference Copenhaver5], and these results were extended by Heuberger and Prodinger [Reference Heuberger and Prodinger14]. A study of
$n$
vertices along with expected values [Reference Copenhaver5], and these results were extended by Heuberger and Prodinger [Reference Heuberger and Prodinger14]. A study of
![]() $k$
-protected vertices in binary search trees was done by Bóna [Reference Bóna2] and Bóna and Pittel [Reference Bóna and Pittel3]. Holmgren and Janson [Reference Holmgren and Janson16] proved general limit theorems for fringe subtrees and related tree functionals, applications of which include a normal limit law for the number of
$k$
-protected vertices in binary search trees was done by Bóna [Reference Bóna2] and Bóna and Pittel [Reference Bóna and Pittel3]. Holmgren and Janson [Reference Holmgren and Janson16] proved general limit theorems for fringe subtrees and related tree functionals, applications of which include a normal limit law for the number of
![]() $k$
-protected vertices in binary search trees and random recursive trees.
$k$
-protected vertices in binary search trees and random recursive trees.
Moreover, the protection number of the root of families of trees has also been studied. In [Reference Heuberger and Prodinger14], Heuberger and Prodinger derived the probability of a plane tree having a root that is
![]() $k$
-protected, the probability distribution of the protection number of the root of recursive trees is determined by Gołȩbiewski and Klimczak in [13]. The protection number of the root in simply generated trees, Pólya trees, and unlabelled non-plane binary trees was studied by Gittenberger, Gołȩbiewski, Larcher, and Sulkowska in [Reference Gittenberger, Gołȩbiewski, Larcher and Sulkowska12], where they also obtained results relating to the protection number of a randomly chosen vertex.
$k$
-protected, the probability distribution of the protection number of the root of recursive trees is determined by Gołȩbiewski and Klimczak in [13]. The protection number of the root in simply generated trees, Pólya trees, and unlabelled non-plane binary trees was studied by Gittenberger, Gołȩbiewski, Larcher, and Sulkowska in [Reference Gittenberger, Gołȩbiewski, Larcher and Sulkowska12], where they also obtained results relating to the protection number of a randomly chosen vertex.
Very recently, Devroye et al. [Reference Devroye, Goh and Zhao6] studied the maximum protection number in Bienaymé–Galton–Watson trees, referring to it as the leaf-height. Specifically, they showed the following: if
![]() $X_n$
is the maximum protection number in a Bienaymé–Galton–Watson tree conditioned on having
$X_n$
is the maximum protection number in a Bienaymé–Galton–Watson tree conditioned on having
![]() $n$
vertices, then
$n$
vertices, then
![]() $\frac{X_n}{\log n}$
converges in probability to a constant if there is a positive probability that a vertex has exactly one child. If this is not the case, then
$\frac{X_n}{\log n}$
converges in probability to a constant if there is a positive probability that a vertex has exactly one child. If this is not the case, then
![]() $\frac{X_n}{\log \log n}$
converges in probability to a constant.
$\frac{X_n}{\log \log n}$
converges in probability to a constant.
Our aim in this paper is to refine the result of Devroye, Goh and Zhao by providing the full limiting distribution of the maximum protection number. For our analytic approach, the framework of simply generated trees is more natural than the probabilistic setting of Bienaymé–Galton–Watson trees, though as mentioned earlier the two are largely equivalent.
1.3 Statement of results
As was already observed by Devroye et al. in [Reference Devroye, Goh and Zhao6], there are two fundamentally different cases to be considered, depending on whether or not vertices of outdegree
![]() $1$
are allowed (have nonzero weight) in the given family of simply generated trees. If such vertices can occur, then we find that the maximum protection number of a random tree with
$1$
are allowed (have nonzero weight) in the given family of simply generated trees. If such vertices can occur, then we find that the maximum protection number of a random tree with
![]() $n$
vertices is on average of order
$n$
vertices is on average of order
![]() $\log n$
, with a discrete double-exponential distribution in the limit. On the other hand, if there are no vertices of outdegree
$\log n$
, with a discrete double-exponential distribution in the limit. On the other hand, if there are no vertices of outdegree
![]() $1$
, then the maximum protection number is on average of order
$1$
, then the maximum protection number is on average of order
![]() $\log \log n$
. There is an intuitive explanation for this phenomenon. If outdegree
$\log \log n$
. There is an intuitive explanation for this phenomenon. If outdegree
![]() $1$
is allowed, it becomes easy to create vertices with high protection number: if the subtree rooted at a vertex is an
$1$
is allowed, it becomes easy to create vertices with high protection number: if the subtree rooted at a vertex is an
![]() $(h+1)$
-vertex path, then this vertex has protection number
$(h+1)$
-vertex path, then this vertex has protection number
![]() $h$
. On the other hand, if outdegree
$h$
. On the other hand, if outdegree
![]() $1$
is forbidden, then the smallest possible subtree rooted at a vertex of protection number
$1$
is forbidden, then the smallest possible subtree rooted at a vertex of protection number
![]() $h$
is a complete binary tree with
$h$
is a complete binary tree with
![]() $2^{h+1}-1$
vertices. An illustration of the two cases is given in Fig. 2.
$2^{h+1}-1$
vertices. An illustration of the two cases is given in Fig. 2.

Figure 2. Smallest examples where a tree may (a) or may not (b) have exactly one child and the root has protection number
![]() $4$
.
$4$
.
In the case where vertices of outdegree
![]() $1$
can occur, the limiting distribution turns out to be a discrete double-exponential distribution that also occurs in many other combinatorial examples, and for which general results are available – see Section 2.2. These results are adapted in Section 5.2 to the case where there are no vertices of outdegree
$1$
can occur, the limiting distribution turns out to be a discrete double-exponential distribution that also occurs in many other combinatorial examples, and for which general results are available – see Section 2.2. These results are adapted in Section 5.2 to the case where there are no vertices of outdegree
![]() $1$
.
$1$
.
In the following results, we make a common technical assumption, stating formally that there is a positive real number
![]() $\tau$
, less than the radius of convergence of
$\tau$
, less than the radius of convergence of
![]() $\Phi$
, such that
$\Phi$
, such that
![]() $\Phi (\tau ) = \tau \Phi '(\tau )$
(see Section 2.1 for further details). This is equivalent to the offspring distribution of the associated Bienaymé–Galton–Watson process having a finite exponential moment, which is the case for all the examples mentioned earlier (plane trees, binary trees, pruned binary trees, and labelled trees). This assumption is crucial for the analytic techniques that we are using, which are based on an asymptotic analysis of generating functions. However, it is quite likely that our main results remain valid under somewhat milder conditions.
$\Phi (\tau ) = \tau \Phi '(\tau )$
(see Section 2.1 for further details). This is equivalent to the offspring distribution of the associated Bienaymé–Galton–Watson process having a finite exponential moment, which is the case for all the examples mentioned earlier (plane trees, binary trees, pruned binary trees, and labelled trees). This assumption is crucial for the analytic techniques that we are using, which are based on an asymptotic analysis of generating functions. However, it is quite likely that our main results remain valid under somewhat milder conditions.
Theorem 1.2.
Given a family of simply generated trees with
![]() $w_1 = \Phi '(0) \neq 0$
, the proportion of trees of size
$w_1 = \Phi '(0) \neq 0$
, the proportion of trees of size
![]() $n$
whose maximum protection number is at most
$n$
whose maximum protection number is at most
![]() $h$
is asymptotically given by
$h$
is asymptotically given by
as
![]() $n \to \infty$
and
$n \to \infty$
and
![]() $h = \log _d\!(n) + O(1)$
, where
$h = \log _d\!(n) + O(1)$
, where
![]() $\kappa$
(given in (55)) and
$\kappa$
(given in (55)) and
![]() $d = (\rho \Phi '(0))^{-1} \gt 1$
are positive constants, with
$d = (\rho \Phi '(0))^{-1} \gt 1$
are positive constants, with
![]() $\rho$
as defined in (3). Moreover, the expected value of the maximum protection number in trees with
$\rho$
as defined in (3). Moreover, the expected value of the maximum protection number in trees with
![]() $n$
vertices is
$n$
vertices is
where
![]() $\gamma$
denotes the Euler–Mascheroni constant and
$\gamma$
denotes the Euler–Mascheroni constant and
![]() $\psi _d$
is the
$\psi _d$
is the
![]() $1$
-periodic function that is defined by the Fourier series
$1$
-periodic function that is defined by the Fourier series
 \begin{equation} \psi _d(x) = -\frac{1}{\log\!(d)}\sum _{k \neq 0}\Gamma \Big ({-}\frac{2k\pi i}{\log\!(d)}\Big )e^{2k\pi i x}. \end{equation}
\begin{equation} \psi _d(x) = -\frac{1}{\log\!(d)}\sum _{k \neq 0}\Gamma \Big ({-}\frac{2k\pi i}{\log\!(d)}\Big )e^{2k\pi i x}. \end{equation}
In the case where vertices of outdegree
![]() $1$
are excluded, we show that the maximum protection number is strongly concentrated. In fact, with high probability it only takes on one of at most two different values (depending on the size of the tree). The precise result can be stated as follows.
$1$
are excluded, we show that the maximum protection number is strongly concentrated. In fact, with high probability it only takes on one of at most two different values (depending on the size of the tree). The precise result can be stated as follows.
Theorem 1.3.
Given a family of simply generated trees with
![]() $w_1 = \Phi '(0) = 0$
, set
$w_1 = \Phi '(0) = 0$
, set
![]() $r = \min \{i \in \mathbb{N}\colon i\,{\geq}\,2 \text{ and } w_i \neq 0\}$
and
$r = \min \{i \in \mathbb{N}\colon i\,{\geq}\,2 \text{ and } w_i \neq 0\}$
and
![]() $D=\gcd \{i\in \mathbb{N} \colon w_i\neq 0\}$
. The proportion of trees of size
$D=\gcd \{i\in \mathbb{N} \colon w_i\neq 0\}$
. The proportion of trees of size
![]() $n$
whose maximum protection number is at most
$n$
whose maximum protection number is at most
![]() $h$
is asymptotically given by
$h$
is asymptotically given by
as
![]() $n \to \infty$
,
$n \to \infty$
,
![]() $n\equiv 1\pmod D$
, and
$n\equiv 1\pmod D$
, and
![]() $h = \log _r{(\log _d\!(n))} + O(1)$
, where
$h = \log _r{(\log _d\!(n))} + O(1)$
, where
![]() $\kappa = \frac{w_r \lambda _1^r}{\Phi (\tau )}$
and
$\kappa = \frac{w_r \lambda _1^r}{\Phi (\tau )}$
and
![]() $d = \mu ^{-r} \gt 1$
are positive constants with
$d = \mu ^{-r} \gt 1$
are positive constants with
![]() $\lambda _1$
and
$\lambda _1$
and
![]() $\mu$
defined in (61) and (62) respectively (see Lemma 5.5). Moreover, there is a sequence of positive integers
$\mu$
defined in (61) and (62) respectively (see Lemma 5.5). Moreover, there is a sequence of positive integers
![]() $h_n$
such that the maximum protection number of a tree with
$h_n$
such that the maximum protection number of a tree with
![]() $n$
vertices is
$n$
vertices is
![]() $h_n$
or
$h_n$
or
![]() $h_n+1$
with high probability (i.e., probability tending to
$h_n+1$
with high probability (i.e., probability tending to
![]() $1$
as
$1$
as
![]() $n \to \infty$
) where
$n \to \infty$
) where
![]() $n\equiv 1\pmod D$
.
$n\equiv 1\pmod D$
.
Specifically, with
![]() $m_n = \log _r{\log _d{(n)}}$
and
$m_n = \log _r{\log _d{(n)}}$
and
![]() $\{m_n\}$
denoting its fractional part, one can set
$\{m_n\}$
denoting its fractional part, one can set
 \begin{equation*} h_n = \begin {cases} \lfloor m_n \rfloor & \textit{if } \{m_n\} \leq \frac 12, \\ \lceil m_n \rceil & \textit{if } \{m_n\} \gt \frac 12. \end {cases} \end{equation*}
\begin{equation*} h_n = \begin {cases} \lfloor m_n \rfloor & \textit{if } \{m_n\} \leq \frac 12, \\ \lceil m_n \rceil & \textit{if } \{m_n\} \gt \frac 12. \end {cases} \end{equation*}
If we restrict to those values of
![]() $n$
for which
$n$
for which
![]() $\{m_n\} \in [\varepsilon,1-\varepsilon ]$
, where
$\{m_n\} \in [\varepsilon,1-\varepsilon ]$
, where
![]() $\varepsilon \gt 0$
is fixed, then with high probability
$\varepsilon \gt 0$
is fixed, then with high probability
![]() $X_n$
is equal to
$X_n$
is equal to
![]() $\lceil m_n \rceil$
.
$\lceil m_n \rceil$
.
Note that in the setting of Theorem 1.3, it is easy to see that there are no trees of size
![]() $n$
if
$n$
if
![]() $n\not \equiv 1\pmod D$
. In the setting of Theorem 1.2, we have
$n\not \equiv 1\pmod D$
. In the setting of Theorem 1.2, we have
![]() $\gcd \{i\in \mathbb{N}\colon w_i\neq 0\}=1$
because
$\gcd \{i\in \mathbb{N}\colon w_i\neq 0\}=1$
because
![]() $w_1\neq 0$
. Theorem 1.2 is illustrated in Fig. 3, while Theorem 1.3 is illustrated in Fig. 4.
$w_1\neq 0$
. Theorem 1.2 is illustrated in Fig. 3, while Theorem 1.3 is illustrated in Fig. 4.

Figure 3. The asymptotic cumulative distribution function plotted against calculated values for plane, binary, and Cayley trees.

Figure 4. The asymptotic cumulative distribution function plotted against calculated values for complete binary, and Riordan trees [Reference Kim and Stanley18].
The proof of Theorem 1.2 relies on a general distributional result provided in [Reference Prodinger and Wagner23], see Theorem 2.1. For the proof of Theorem 1.3, however, we will need a variant for doubly exponential convergence of the dominant singularities. The statement and proof are similar to the original and we expect that this variant will be useful in other contexts, too.
Theorem 1.4.
Let
![]() $Y_h(x) = \sum _{n \geq 0} y_{h, n}x^n$
(
$Y_h(x) = \sum _{n \geq 0} y_{h, n}x^n$
(
![]() $h \geq 0$
) be a sequence of generating functions with nonnegative coefficients such that
$h \geq 0$
) be a sequence of generating functions with nonnegative coefficients such that
![]() $y_{h, n}$
is nondecreasing in
$y_{h, n}$
is nondecreasing in
![]() $h$
and (coefficientwise)
$h$
and (coefficientwise)
and let
![]() $X_n$
denote the sequence of random variables with support
$X_n$
denote the sequence of random variables with support
![]() $\mathbb{N}_0$
defined by
$\mathbb{N}_0$
defined by
Assume that each generating function
![]() $Y_h$
has a singularity at
$Y_h$
has a singularity at
![]() $\rho _h \in \mathbb{R}$
such that
$\rho _h \in \mathbb{R}$
such that
-
(1)
 $\rho _h = \rho (1+ \kappa \zeta ^{r^{h}} + o(\zeta ^{r^{h}}))$
as
$\rho _h = \rho (1+ \kappa \zeta ^{r^{h}} + o(\zeta ^{r^{h}}))$
as
 $h \to \infty$
for some constants
$h \to \infty$
for some constants
 $\rho \gt 0$
,
$\rho \gt 0$
,
 $\kappa \gt 0$
,
$\kappa \gt 0$
,
 $\zeta \in (0, 1)$
, and
$\zeta \in (0, 1)$
, and
 $r \gt 1$
.
$r \gt 1$
. -
(2)
 $Y_h(x)$
can be continued analytically to the domain
for some fixed
$Y_h(x)$
can be continued analytically to the domain
for some fixed \begin{equation*} \{x \in \mathbb {C} \,{:}\, |{x}| \leq (1+\delta )|{\rho _h}|, |{\mathrm {Arg}(x/\rho _h - 1)}| \gt \phi \} \end{equation*}
\begin{equation*} \{x \in \mathbb {C} \,{:}\, |{x}| \leq (1+\delta )|{\rho _h}|, |{\mathrm {Arg}(x/\rho _h - 1)}| \gt \phi \} \end{equation*}
 $\delta \gt 0$
and
$\delta \gt 0$
and
 $\phi \in (0, \pi/2)$
, and
holds within this domain, uniformly in
$\phi \in (0, \pi/2)$
, and
holds within this domain, uniformly in \begin{equation*} Y_h(x) = U_h(x) + A_h(1-x/\rho _h)^\alpha + o((1 - x/\rho _h)^\alpha ) \end{equation*}
\begin{equation*} Y_h(x) = U_h(x) + A_h(1-x/\rho _h)^\alpha + o((1 - x/\rho _h)^\alpha ) \end{equation*}
 $h$
, where
$h$
, where
 $U_h(x)$
is analytic and uniformly bounded in
$U_h(x)$
is analytic and uniformly bounded in
 $h$
within the aforementioned region,
$h$
within the aforementioned region,
 $\alpha \in \mathbb{R} \setminus \mathbb{N}_0$
, and
$\alpha \in \mathbb{R} \setminus \mathbb{N}_0$
, and
 $A_h$
is a constant dependent on
$A_h$
is a constant dependent on
 $h$
such that
$h$
such that
 $\lim _{h \to \infty }A_h = A\neq 0$
. Finally,
in the region
$\lim _{h \to \infty }A_h = A\neq 0$
. Finally,
in the region \begin{equation*} Y(x) = U(x) + A (1-x/\rho )^\alpha + o((1-x/\rho )^\alpha ) \end{equation*}
for a function
\begin{equation*} Y(x) = U(x) + A (1-x/\rho )^\alpha + o((1-x/\rho )^\alpha ) \end{equation*}
for a function \begin{equation*} \{x \in \mathbb {C} \,{:}\, |{x}| \leq (1+\delta )|{\rho }|, |\mathrm {Arg}(x/\rho - 1)| \gt \phi \} \end{equation*}
\begin{equation*} \{x \in \mathbb {C} \,{:}\, |{x}| \leq (1+\delta )|{\rho }|, |\mathrm {Arg}(x/\rho - 1)| \gt \phi \} \end{equation*}
 $U(x)$
that is analytic within this region.
$U(x)$
that is analytic within this region.
Then the asymptotic formula
holds as
![]() $n \to \infty$
and
$n \to \infty$
and
![]() $h = \log _r{(\log _d{(n)})} + O(1)$
, where
$h = \log _r{(\log _d{(n)})} + O(1)$
, where
![]() $d = \zeta ^{-1}$
.
$d = \zeta ^{-1}$
.
Note that here we have
![]() $\rho _h = \rho (1+ \kappa \zeta ^{r^{h}} + o(\zeta ^{r^{h}}))$
, while in Theorem 2.1 we have the exponential case
$\rho _h = \rho (1+ \kappa \zeta ^{r^{h}} + o(\zeta ^{r^{h}}))$
, while in Theorem 2.1 we have the exponential case
![]() $\rho _h = \rho (1+ \kappa \zeta ^h + o(\zeta ^h))$
.
$\rho _h = \rho (1+ \kappa \zeta ^h + o(\zeta ^h))$
.
In the next theorem, we show that the consequences of this distributional result are quite drastic.
Theorem 1.5.
Assume the conditions of Theorem
1.4
. There is a sequence of nonnegative integers
![]() $h_n$
such that
$h_n$
such that
![]() $X_n$
is equal to
$X_n$
is equal to
![]() $h_n$
or
$h_n$
or
![]() $h_n+1$
with high probability. Specifically, with
$h_n+1$
with high probability. Specifically, with
![]() $m_n = \log _r{\log _d{(n)}}$
and
$m_n = \log _r{\log _d{(n)}}$
and
![]() $\{m_n\}$
denoting its fractional part, one can set
$\{m_n\}$
denoting its fractional part, one can set
 \begin{equation*} h_n = \begin {cases} \lfloor m_n \rfloor & \text {if } \{m_n\} \leq \frac 12, \\ \lceil m_n \rceil & \text {if } \{m_n\} \gt \frac 12. \end {cases} \end{equation*}
\begin{equation*} h_n = \begin {cases} \lfloor m_n \rfloor & \text {if } \{m_n\} \leq \frac 12, \\ \lceil m_n \rceil & \text {if } \{m_n\} \gt \frac 12. \end {cases} \end{equation*}
If we restrict to those values of
![]() $n$
for which
$n$
for which
![]() $\{m_n\} \in [\varepsilon,1-\varepsilon ]$
, where
$\{m_n\} \in [\varepsilon,1-\varepsilon ]$
, where
![]() $\varepsilon \gt 0$
is fixed, then with high probability
$\varepsilon \gt 0$
is fixed, then with high probability
![]() $X_n$
is equal to
$X_n$
is equal to
![]() $\lceil m_n \rceil$
.
$\lceil m_n \rceil$
.
2. Preliminaries
2.1 Basic facts about simply generated trees
For our purposes, we will make the following typical technical assumptions: first, we assume without loss of generality that
![]() $w_0 = 1$
or equivalently
$w_0 = 1$
or equivalently
![]() $\Phi (0) = 1$
. In other words, leaves have an associated weight of
$\Phi (0) = 1$
. In other words, leaves have an associated weight of
![]() $1$
, which can be achieved by means of a normalising factor if necessary. Moreover, to avoid trivial cases in which the only possible trees are paths, we assume that
$1$
, which can be achieved by means of a normalising factor if necessary. Moreover, to avoid trivial cases in which the only possible trees are paths, we assume that
![]() $w_j \gt 0$
for at least one
$w_j \gt 0$
for at least one
![]() $j \geq 2$
. Finally, we assume that there is a positive real number
$j \geq 2$
. Finally, we assume that there is a positive real number
![]() $\tau$
, less than the radius of convergence of
$\tau$
, less than the radius of convergence of
![]() $\Phi$
, such that
$\Phi$
, such that
![]() $\Phi (\tau ) = \tau \Phi '(\tau )$
. As mentioned earlier, this is equivalent to the offspring distribution having exponential moments.
$\Phi (\tau ) = \tau \Phi '(\tau )$
. As mentioned earlier, this is equivalent to the offspring distribution having exponential moments.
It is well known (see e.g. [Reference Drmota8, Section 3.1.4]) that if such a
![]() $\tau$
exists, it is unique, and the radius of convergence
$\tau$
exists, it is unique, and the radius of convergence
![]() $\rho$
of
$\rho$
of
![]() $Y$
can be expressed as
$Y$
can be expressed as
which is equivalent to
![]() $\rho$
and
$\rho$
and
![]() $\tau$
satisfying the simultaneous equations
$\tau$
satisfying the simultaneous equations
![]() $y = x \Phi (y)$
and
$y = x \Phi (y)$
and
![]() $1 = x \Phi '(y)$
(which essentially mean that the implicit function theorem fails at the point
$1 = x \Phi '(y)$
(which essentially mean that the implicit function theorem fails at the point
![]() $(\rho,\tau )$
). Moreover,
$(\rho,\tau )$
). Moreover,
![]() $Y$
has a square root singularity at
$Y$
has a square root singularity at
![]() $\rho$
with
$\rho$
with
![]() $\tau = Y(\rho )$
, with a singular expansion of the form
$\tau = Y(\rho )$
, with a singular expansion of the form
The coefficients
![]() $a,b,c$
can be expressed in terms of
$a,b,c$
can be expressed in terms of
![]() $\Phi$
and
$\Phi$
and
![]() $\tau$
. In particular, we have
$\tau$
. In particular, we have
In fact, there is a full Newton–Puiseux expansion in powers of
![]() $(1-x/\rho )^{1/2}$
. If the weight sequence is aperiodic, i.e.,
$(1-x/\rho )^{1/2}$
. If the weight sequence is aperiodic, i.e.,
![]() $\gcd \{j \colon w_j \neq 0\} = 1$
, then
$\gcd \{j \colon w_j \neq 0\} = 1$
, then
![]() $\rho$
is the only singularity on the circle of convergence of
$\rho$
is the only singularity on the circle of convergence of
![]() $Y$
, and for sufficiently small
$Y$
, and for sufficiently small
![]() $\varepsilon \gt 0$
there are no solutions to the simultaneous equations
$\varepsilon \gt 0$
there are no solutions to the simultaneous equations
![]() $y = x \Phi (y)$
and
$y = x \Phi (y)$
and
![]() $1 = x \Phi '(y)$
with
$1 = x \Phi '(y)$
with
![]() $|{x}| \leq \rho + \varepsilon$
and
$|{x}| \leq \rho + \varepsilon$
and
![]() $|{y}| \leq \tau + \varepsilon$
other than
$|{y}| \leq \tau + \varepsilon$
other than
![]() $(x,y) = (\rho,\tau )$
. Otherwise, if this
$(x,y) = (\rho,\tau )$
. Otherwise, if this
![]() $\gcd$
is equal to
$\gcd$
is equal to
![]() $D$
, there are
$D$
, there are
![]() $D$
singularities at
$D$
singularities at
![]() $\rho e^{2k\pi i/D}$
(
$\rho e^{2k\pi i/D}$
(
![]() $i \in \{0,1,\ldots,D-1\}$
), all with the same singular behaviour. In the following, we assume for technical simplicity that the weight sequence is indeed aperiodic, but the proofs are readily adapted to the periodic setting, see Remarks 3.17 and 5.9.
$i \in \{0,1,\ldots,D-1\}$
), all with the same singular behaviour. In the following, we assume for technical simplicity that the weight sequence is indeed aperiodic, but the proofs are readily adapted to the periodic setting, see Remarks 3.17 and 5.9.
By means of singularity analysis [Reference Flajolet and Sedgewick10, Chapter VI], the singular expansion (4) yields an asymptotic formula for the coefficients of
![]() $Y$
: we have
$Y$
: we have
If the weight sequence corresponds to a probability distribution, then
![]() $y_n$
is the probability that an unconditioned Bienaymé–Galton–Watson tree has exactly
$y_n$
is the probability that an unconditioned Bienaymé–Galton–Watson tree has exactly
![]() $n$
vertices when the process ends. For other classes such as plane trees or binary trees,
$n$
vertices when the process ends. For other classes such as plane trees or binary trees,
![]() $y_n$
represents the number of
$y_n$
represents the number of
![]() $n$
-vertex trees in the respective class.
$n$
-vertex trees in the respective class.
2.2 A general distributional result
The discrete double-exponential distribution in Theorem 1.2 has been observed in many other combinatorial instances, for example the longest run of zeros in a random
![]() $0$
-
$0$
-
![]() $1$
-string, the longest horizontal segment in Motzkin paths or the maximum outdegree in plane trees. This can often be traced back to the behaviour of the singularities of associated generating functions. The following general result [Reference Prodinger and Wagner23], similar to Theorem 1.4 but with an exponential instead of doubly exponential rate of convergence of the dominant singularity, will be a key tool for us.
$1$
-string, the longest horizontal segment in Motzkin paths or the maximum outdegree in plane trees. This can often be traced back to the behaviour of the singularities of associated generating functions. The following general result [Reference Prodinger and Wagner23], similar to Theorem 1.4 but with an exponential instead of doubly exponential rate of convergence of the dominant singularity, will be a key tool for us.
Theorem 2.1 (see [Reference Prodinger and Wagner23, Theorem 1]). Let
![]() $Y_h(x) = \sum _{n \geq 0}y_{h, n}x^n$
$Y_h(x) = \sum _{n \geq 0}y_{h, n}x^n$
![]() $(h \geq 0)$
be a sequence of generating functions with nonnegative coefficients such that
$(h \geq 0)$
be a sequence of generating functions with nonnegative coefficients such that
![]() $y_{h, n}$
is nondecreasing in
$y_{h, n}$
is nondecreasing in
![]() $h$
and (coefficientwise)
$h$
and (coefficientwise)
and let
![]() $X_n$
denote the sequence of random variables with support
$X_n$
denote the sequence of random variables with support
![]() $\mathbb{N}_0$
defined by
$\mathbb{N}_0$
defined by
Assume, moreover, that each generating function
![]() $Y_h$
has a singularity
$Y_h$
has a singularity
![]() $\rho _h \in{\mathbb{R}}$
, such that
$\rho _h \in{\mathbb{R}}$
, such that
-
(1)
 $\rho _h = \rho (1+ \kappa \zeta ^h + o(\zeta ^h))$
as
$\rho _h = \rho (1+ \kappa \zeta ^h + o(\zeta ^h))$
as
 $h \to \infty$
for some constants
$h \to \infty$
for some constants
 $\rho \gt 0$
,
$\rho \gt 0$
,
 $\kappa \gt 0$
and
$\kappa \gt 0$
and
 $\zeta \in (0, 1)$
.
$\zeta \in (0, 1)$
. -
(2)
 $Y_h(x)$
can be continued analytically to the domain
(6)for some fixed
$Y_h(x)$
can be continued analytically to the domain
(6)for some fixed \begin{equation} \{x \in{\mathbb{C}}\,{:}\, |{x}| \leq (1 + \delta )|{\rho _h}|, |\mathrm{Arg}(x/\rho _h - 1)| \gt \phi \} \end{equation}
\begin{equation} \{x \in{\mathbb{C}}\,{:}\, |{x}| \leq (1 + \delta )|{\rho _h}|, |\mathrm{Arg}(x/\rho _h - 1)| \gt \phi \} \end{equation}
 $\delta \gt 0$
and
$\delta \gt 0$
and
 $\phi \in (0, \pi/2)$
, and
holds within this domain, uniformly in
$\phi \in (0, \pi/2)$
, and
holds within this domain, uniformly in \begin{equation*} Y_h(x) = U_h(x) + A_h(1-x/\rho _h)^\alpha + o((1-x/\rho _h)^\alpha ) \end{equation*}
\begin{equation*} Y_h(x) = U_h(x) + A_h(1-x/\rho _h)^\alpha + o((1-x/\rho _h)^\alpha ) \end{equation*}
 $h$
, where
$h$
, where
 $U_h(x)$
is analytic and uniformly bounded in
$U_h(x)$
is analytic and uniformly bounded in
 $h$
within the aforementioned region,
$h$
within the aforementioned region,
 $\alpha \in{\mathbb{R}} \setminus \mathbb{N}_0$
, and
$\alpha \in{\mathbb{R}} \setminus \mathbb{N}_0$
, and
 $A_h$
is a constant depending on
$A_h$
is a constant depending on
 $h$
such that
$h$
such that
 $\lim _{h \to \infty }A_h = A\neq 0$
. Finally,
in the region
$\lim _{h \to \infty }A_h = A\neq 0$
. Finally,
in the region \begin{equation*} Y(x) = U(x) + A(1-x/\rho )^\alpha + o((1-x/\rho )^\alpha ) \end{equation*}
for a function
\begin{equation*} Y(x) = U(x) + A(1-x/\rho )^\alpha + o((1-x/\rho )^\alpha ) \end{equation*}
for a function \begin{equation*} \{x \in {\mathbb {C}}\,{:}\, |{x}| \leq (1 + \delta )|{\rho }|, |\mathrm {Arg}(x/\rho - 1)| \gt \phi \} \end{equation*}
\begin{equation*} \{x \in {\mathbb {C}}\,{:}\, |{x}| \leq (1 + \delta )|{\rho }|, |\mathrm {Arg}(x/\rho - 1)| \gt \phi \} \end{equation*}
 $U(x)$
that is analytic within this region.
$U(x)$
that is analytic within this region.
Then the asymptotic formula
holds as
![]() $n \to \infty$
and
$n \to \infty$
and
![]() $h = \log _d\!(n) + O(1)$
, where
$h = \log _d\!(n) + O(1)$
, where
![]() $d = \zeta ^{-1}$
. Hence the shifted random variable
$d = \zeta ^{-1}$
. Hence the shifted random variable
![]() $X_n - \log _d\!(n)$
converges weakly to a limiting distribution if
$X_n - \log _d\!(n)$
converges weakly to a limiting distribution if
![]() $n$
runs through a subset of the positive integers such that the fractional part
$n$
runs through a subset of the positive integers such that the fractional part
![]() $\{\log _d\!(n)\}$
of
$\{\log _d\!(n)\}$
of
![]() $\log _d\!(n)$
converges.
$\log _d\!(n)$
converges.
As we will see, the conditions of this theorem hold for the random variable
![]() $X_n$
given by the maximum protection number of a random
$X_n$
given by the maximum protection number of a random
![]() $n$
-vertex tree from a simply generated family that satisfies our technical assumptions. Under slightly stronger assumptions, which also hold in our case, one has the following theorem on the expected value of the random variable
$n$
-vertex tree from a simply generated family that satisfies our technical assumptions. Under slightly stronger assumptions, which also hold in our case, one has the following theorem on the expected value of the random variable
![]() $X_n$
.
$X_n$
.
Theorem 2.2 (see [Reference Prodinger and Wagner23, Theorem 2]). In the setting of Theorem 2.1 , assume additionally that
-
(1) There exists a constant
 $K$
such that
$K$
such that
 $y_{h, n} = y_n$
for
$y_{h, n} = y_n$
for
 $h \gt Kn$
,
$h \gt Kn$
, -
(2)
 $\sum _{h \geq 0} |{A - A_h}| \lt \infty$
,
$\sum _{h \geq 0} |{A - A_h}| \lt \infty$
, -
(3) the asymptotic expansions of
 $Y_h$
and
$Y_h$
and
 $Y$
around their singularities are given by
$Y$
around their singularities are given by
 \begin{equation*} Y_h(x) = U_h(x) + A_h(1 - x/\rho _h)^\alpha + B_h(1 - x/\rho _h)^{\alpha +1} + o((1 - x/\rho _h)^{\alpha +1}), \end{equation*}
\begin{equation*} Y_h(x) = U_h(x) + A_h(1 - x/\rho _h)^\alpha + B_h(1 - x/\rho _h)^{\alpha +1} + o((1 - x/\rho _h)^{\alpha +1}), \end{equation*}
uniformly in
 $h$
, and
respectively, such that
$h$
, and
respectively, such that \begin{equation*} Y(x) = U(x) + A(1 - x/\rho _h)^\alpha + B(1 - x/\rho _h)^{\alpha +1} + o((1 - x/\rho _h)^{\alpha +1}), \end{equation*}
\begin{equation*} Y(x) = U(x) + A(1 - x/\rho _h)^\alpha + B(1 - x/\rho _h)^{\alpha +1} + o((1 - x/\rho _h)^{\alpha +1}), \end{equation*}
 $\lim _{h\to \infty } B_h = B$
.
$\lim _{h\to \infty } B_h = B$
.
Then the mean of
![]() $X_n$
satisfies
$X_n$
satisfies
where
![]() $\gamma$
denotes the Euler–Mascheroni constant and
$\gamma$
denotes the Euler–Mascheroni constant and
![]() $\psi _d$
is given by (2).
$\psi _d$
is given by (2).
2.3 A system of functional equations
As a first step of our analysis, we consider a number of auxiliary generating functions and derive a system of functional equations that is satisfied by these generating functions. The family of simply generated trees and the associated weight generating function
![]() $\Phi$
are regarded fixed throughout. Let
$\Phi$
are regarded fixed throughout. Let
![]() $h$
be a positive integer and
$h$
be a positive integer and
![]() $k$
an integer with
$k$
an integer with
![]() $0 \leq k \leq h$
. Consider trees with the following two properties:
$0 \leq k \leq h$
. Consider trees with the following two properties:
-
P1. No vertex has a protection number greater than
 $h$
.
$h$
. -
P2. The root is
 $k$
-protected (but also has protection number at most
$k$
-protected (but also has protection number at most
 $h$
).
$h$
).
Let
![]() $Y_{h, k}(x)$
be the associated generating function, where
$Y_{h, k}(x)$
be the associated generating function, where
![]() $x$
marks the number of vertices. Note in particular that when
$x$
marks the number of vertices. Note in particular that when
![]() $k = 0$
, we obtain the generating function for trees where the maximum protection number is at most
$k = 0$
, we obtain the generating function for trees where the maximum protection number is at most
![]() $h$
. Hence we can express the probability that the maximum protection number of a random
$h$
. Hence we can express the probability that the maximum protection number of a random
![]() $n$
-vertex tree (from our simply generated family) is at most
$n$
-vertex tree (from our simply generated family) is at most
![]() $h$
as the quotient
$h$
as the quotient
This is precisely the form of (5), and indeed our general strategy will be to show that the generating functions
![]() $Y_{h,0}$
satisfy the technical conditions of Theorem 2.1. Compared to the examples given in [Reference Prodinger and Wagner23], this will be a rather lengthy technical task. However, we believe that the general method, in which a sequence of functional equations is shown to converge uniformly in a suitable region, is also potentially applicable to other instances and therefore interesting in its own right.
$Y_{h,0}$
satisfy the technical conditions of Theorem 2.1. Compared to the examples given in [Reference Prodinger and Wagner23], this will be a rather lengthy technical task. However, we believe that the general method, in which a sequence of functional equations is shown to converge uniformly in a suitable region, is also potentially applicable to other instances and therefore interesting in its own right.
Let us now derive a system of functional equations, using the standard decomposition of a rooted tree into the root and its branches. Clearly, if a tree has property P1, then this must also be the case for all its branches. Moreover, property P2 is satisfied for
![]() $k \gt 0$
if and only if the root of each of the branches is
$k \gt 0$
if and only if the root of each of the branches is
![]() $(k-1)$
-protected, but not all of them are
$(k-1)$
-protected, but not all of them are
![]() $h$
-protected (as this would make the root
$h$
-protected (as this would make the root
![]() $(h+1)$
-protected). Thus, for
$(h+1)$
-protected). Thus, for
![]() $1 \leq k \leq h$
, we have
$1 \leq k \leq h$
, we have
Note that the only case in which the root is only
![]() $0$
-protected is when the root is the only vertex. Hence we have
$0$
-protected is when the root is the only vertex. Hence we have
The analytic properties of the system of functional equations given by (7) and (8) will be studied in the following section, culminating in Proposition 3.16, which shows that Theorem 2.1 is indeed applicable to our problem.
3. Analysis of the functional equations
3.1 Contractions and implicit equations
This section is devoted to a detailed analysis of the generating functions
![]() $Y_{h,k}$
that satisfy the system of equations given by (7) and (8). The first step will be to reduce it to a single implicit equation satisfied by
$Y_{h,k}$
that satisfy the system of equations given by (7) and (8). The first step will be to reduce it to a single implicit equation satisfied by
![]() $Y_{h,1}$
that is then shown to converge to the functional equation (1) in a sense that will be made precise. This is then used to infer information on the region of analyticity of
$Y_{h,1}$
that is then shown to converge to the functional equation (1) in a sense that will be made precise. This is then used to infer information on the region of analyticity of
![]() $Y_{h,1}$
as well as its behaviour around the dominant singularity, which is also shown to converge to the dominant singularity of
$Y_{h,1}$
as well as its behaviour around the dominant singularity, which is also shown to converge to the dominant singularity of
![]() $Y$
. This information is collected in Proposition 3.16 at the end of the section.
$Y$
. This information is collected in Proposition 3.16 at the end of the section.
In the following, we will prove various statements for sufficiently small
![]() $\varepsilon \gt 0$
. In several, but finitely many, steps it might be necessary to decrease
$\varepsilon \gt 0$
. In several, but finitely many, steps it might be necessary to decrease
![]() $\varepsilon$
; we tacitly assume that
$\varepsilon$
; we tacitly assume that
![]() $\varepsilon$
is always small enough to ensure validity of all statements up to the given point. In order to avoid ambiguities, we will always assume that
$\varepsilon$
is always small enough to ensure validity of all statements up to the given point. In order to avoid ambiguities, we will always assume that
![]() $\varepsilon \lt 1$
. Let us remark that
$\varepsilon \lt 1$
. Let us remark that
![]() $\varepsilon$
and other constants as well as all implied
$\varepsilon$
and other constants as well as all implied
![]() $O$
-constants that occur in this section depend on the specific simply generated family of trees (in particular the weight generating function
$O$
-constants that occur in this section depend on the specific simply generated family of trees (in particular the weight generating function
![]() $\Phi$
and therefore
$\Phi$
and therefore
![]() $\rho$
and
$\rho$
and
![]() $\tau$
), but nothing else.
$\tau$
), but nothing else.
Recall that
![]() $\rho$
is the dominant singularity of the generating function
$\rho$
is the dominant singularity of the generating function
![]() $Y$
of our simply generated family of trees. Moreover,
$Y$
of our simply generated family of trees. Moreover,
![]() $\tau = Y(\rho )$
is characterised by the equation
$\tau = Y(\rho )$
is characterised by the equation
![]() $\tau \Phi '(\tau ) = \Phi (\tau )$
(see (3)) and satisfies
$\tau \Phi '(\tau ) = \Phi (\tau )$
(see (3)) and satisfies
![]() $\tau = \rho \Phi (\tau )$
. Since
$\tau = \rho \Phi (\tau )$
. Since
![]() $\Phi$
is increasing and
$\Phi$
is increasing and
![]() $\Phi (0) = 1$
, we also have
$\Phi (0) = 1$
, we also have
![]() $\tau = \rho \Phi (\tau ) \gt \rho \Phi (0) = \rho$
.
$\tau = \rho \Phi (\tau ) \gt \rho \Phi (0) = \rho$
.
Let us write
![]() $D_{\delta }(w) \,{:\!=}\, \{ z \in{\mathbb{C}} \,: \, |{z-w}| \lt \delta \}$
for open disks. For
$D_{\delta }(w) \,{:\!=}\, \{ z \in{\mathbb{C}} \,: \, |{z-w}| \lt \delta \}$
for open disks. For
![]() $\varepsilon \gt 0$
, we define
$\varepsilon \gt 0$
, we define
 \begin{align*} \Xi _\varepsilon ^{(1)}&\,{:\!=}\, D_{\rho +\varepsilon }(0),\\ \Xi _\varepsilon ^{(2)}&\,{:\!=}\, D_{\tau - \rho +\varepsilon }(0),\\ \Xi _\varepsilon ^{(3)}&\,{:\!=}\, D_{\varepsilon }(0). \end{align*}
\begin{align*} \Xi _\varepsilon ^{(1)}&\,{:\!=}\, D_{\rho +\varepsilon }(0),\\ \Xi _\varepsilon ^{(2)}&\,{:\!=}\, D_{\tau - \rho +\varepsilon }(0),\\ \Xi _\varepsilon ^{(3)}&\,{:\!=}\, D_{\varepsilon }(0). \end{align*}
For
![]() $1\le j\lt k\le 3$
, we set
$1\le j\lt k\le 3$
, we set
![]() $\Xi ^{(j, k)}_\varepsilon \,{:\!=}\, \Xi ^{(j)}_\varepsilon \times \Xi ^{(k)}_\varepsilon$
, and we also set
$\Xi ^{(j, k)}_\varepsilon \,{:\!=}\, \Xi ^{(j)}_\varepsilon \times \Xi ^{(k)}_\varepsilon$
, and we also set
![]() $\Xi _{\varepsilon }\,{:\!=}\, \Xi ^{(1, 2, 3)}_{\varepsilon }\,{:\!=}\, \Xi ^{(1)}_\varepsilon \times \Xi ^{(2)}_\varepsilon \times \Xi ^{(3)}_\varepsilon$
. As
$\Xi _{\varepsilon }\,{:\!=}\, \Xi ^{(1, 2, 3)}_{\varepsilon }\,{:\!=}\, \Xi ^{(1)}_\varepsilon \times \Xi ^{(2)}_\varepsilon \times \Xi ^{(3)}_\varepsilon$
. As
![]() $\tau$
is less than the radius of convergence of
$\tau$
is less than the radius of convergence of
![]() $\Phi$
by our assumptions, we may choose
$\Phi$
by our assumptions, we may choose
![]() $\varepsilon \gt 0$
sufficiently small such that
$\varepsilon \gt 0$
sufficiently small such that
![]() $\tau +2\varepsilon$
is still smaller than the radius of convergence of
$\tau +2\varepsilon$
is still smaller than the radius of convergence of
![]() $\Phi$
.
$\Phi$
.
Consider the function defined by
![]() $f_{x, z}(y) = x(\Phi (y)-\Phi (z))$
. We can rewrite the functional equation (7) in terms of this function as
$f_{x, z}(y) = x(\Phi (y)-\Phi (z))$
. We can rewrite the functional equation (7) in terms of this function as
for
![]() $1\le k\le h$
. For
$1\le k\le h$
. For
![]() $j\ge 0$
, we denote the
$j\ge 0$
, we denote the
![]() $j$
th iterate of
$j$
th iterate of
![]() $f_{x, z}$
by
$f_{x, z}$
by
![]() $f^{(j)}_{x, z}$
, i. e.,
$f^{(j)}_{x, z}$
, i. e.,
![]() $f^{(0)}_{x, z}(y) = y$
and
$f^{(0)}_{x, z}(y) = y$
and
![]() $f^{(j+1)}_{x, z}(y)=f_{x, z}^{(j)}(f_{x, z}(y))$
for
$f^{(j+1)}_{x, z}(y)=f_{x, z}^{(j)}(f_{x, z}(y))$
for
![]() $j\ge 0$
. Iterating (9) then yields
$j\ge 0$
. Iterating (9) then yields
for
![]() $1\le k\le h$
and therefore
$1\le k\le h$
and therefore
Plugging (8) into (7) for
![]() $k=1$
yields
$k=1$
yields
This means that (10) and (11) are a system of two functional equations for
![]() $Y_{h, 1}(x)$
and
$Y_{h, 1}(x)$
and
![]() $Y_{h, h}(x)$
. We intend to solve (10) for
$Y_{h, h}(x)$
. We intend to solve (10) for
![]() $Y_{h, h}(x)$
and then plug the solution into (11). As a first step towards this goal, we show that
$Y_{h, h}(x)$
and then plug the solution into (11). As a first step towards this goal, we show that
![]() $f_{x,z}$
represents a contraction on a suitable region.
$f_{x,z}$
represents a contraction on a suitable region.
Lemma 3.1.
For sufficiently small
![]() $\varepsilon \gt 0$
, we have
$\varepsilon \gt 0$
, we have
![]() $|f_{x,z}(y)|\lt \tau -\rho$
for all
$|f_{x,z}(y)|\lt \tau -\rho$
for all
![]() $(x, y, z)\in \Xi _{\varepsilon }$
.
$(x, y, z)\in \Xi _{\varepsilon }$
.
Proof. By the triangle inequality, definition of
![]() $\Xi _{\varepsilon }$
, non-negativity of the coefficients of
$\Xi _{\varepsilon }$
, non-negativity of the coefficients of
![]() $\Phi$
, and
$\Phi$
, and
![]() $\Phi (0)=1$
, we have
$\Phi (0)=1$
, we have
 \begin{align*} |f_{x,z}(y)|&=|x\bigl ((\Phi (y)-1)-(\Phi (z)-1)\bigr )|\\ &\le (\rho +\varepsilon )(|\Phi (y)-1|+|\Phi (z)-1|)\\ &\le (\rho +\varepsilon )((\Phi (|{y}|)-1)+(\Phi (|z|)-1))\\ &\le (\rho +\varepsilon )(\Phi (\tau -\rho +\varepsilon )-1+\Phi (\varepsilon )-1). \end{align*}
\begin{align*} |f_{x,z}(y)|&=|x\bigl ((\Phi (y)-1)-(\Phi (z)-1)\bigr )|\\ &\le (\rho +\varepsilon )(|\Phi (y)-1|+|\Phi (z)-1|)\\ &\le (\rho +\varepsilon )((\Phi (|{y}|)-1)+(\Phi (|z|)-1))\\ &\le (\rho +\varepsilon )(\Phi (\tau -\rho +\varepsilon )-1+\Phi (\varepsilon )-1). \end{align*}
For
![]() $\varepsilon \to 0$
, the upper bound converges to
$\varepsilon \to 0$
, the upper bound converges to
![]() $\rho \Phi (\tau -\rho )-\rho$
because we are assuming that
$\rho \Phi (\tau -\rho )-\rho$
because we are assuming that
![]() $\Phi (0)=1$
. As
$\Phi (0)=1$
. As
![]() $\rho \Phi (\tau -\rho )-\rho \lt \rho \Phi (\tau )-\rho =\tau -\rho$
by (3), the assertion of the lemma holds for sufficiently small
$\rho \Phi (\tau -\rho )-\rho \lt \rho \Phi (\tau )-\rho =\tau -\rho$
by (3), the assertion of the lemma holds for sufficiently small
![]() $\varepsilon \gt 0$
.
$\varepsilon \gt 0$
.
Lemma 3.2.
For sufficiently small
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $(x, y, z) \in \Xi _{\varepsilon }$
, we have
$(x, y, z) \in \Xi _{\varepsilon }$
, we have
![]() $|f'_{x, z}(y)| = |x \Phi '(y)| \leq \lambda$
for some constant
$|f'_{x, z}(y)| = |x \Phi '(y)| \leq \lambda$
for some constant
![]() $\lambda \lt 1$
.
$\lambda \lt 1$
.
Proof. For any triple
![]() $(x, y, z)\in \Xi _{\varepsilon }$
,
$(x, y, z)\in \Xi _{\varepsilon }$
,
For
![]() $\varepsilon \to 0$
, the upper bound converges to
$\varepsilon \to 0$
, the upper bound converges to
![]() $\rho \Phi '(\tau -\rho )$
, which is less than
$\rho \Phi '(\tau -\rho )$
, which is less than
![]() $\rho \Phi '(\tau )=1$
(by (3)).
$\rho \Phi '(\tau )=1$
(by (3)).
For the remainder of this section,
![]() $\lambda$
will be defined as in Lemma 3.2.
$\lambda$
will be defined as in Lemma 3.2.
Lemma 3.3.
For sufficiently small
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $(x, z)\in \Xi _{\varepsilon }^{(1, 3)}$
,
$(x, z)\in \Xi _{\varepsilon }^{(1, 3)}$
,
![]() $f_{x,z}$
maps
$f_{x,z}$
maps
![]() $\Xi _{\varepsilon }^{(2)}$
to itself and is a contraction with Lipschitz constant
$\Xi _{\varepsilon }^{(2)}$
to itself and is a contraction with Lipschitz constant
![]() $\lambda$
.
$\lambda$
.
Proof. The fact that
![]() $f_{x,z}$
maps
$f_{x,z}$
maps
![]() $\Xi _{\varepsilon }^{(2)}$
to itself for sufficiently small
$\Xi _{\varepsilon }^{(2)}$
to itself for sufficiently small
![]() $\varepsilon \gt 0$
is a direct consequence of Lemma 3.1.
$\varepsilon \gt 0$
is a direct consequence of Lemma 3.1.
Making use of Lemma 3.2, the contraction property now follows by a standard argument: For
![]() $y_1$
,
$y_1$
,
![]() $y_2\in \Xi _{\varepsilon }^{(2)}$
, we have
$y_2\in \Xi _{\varepsilon }^{(2)}$
, we have
For sufficiently small
![]() $\varepsilon$
and
$\varepsilon$
and
![]() $(x, z)\in \Xi _{\varepsilon }^{(1, 3)}$
, Banach’s fixed point theorem together with Lemma 3.3 implies that
$(x, z)\in \Xi _{\varepsilon }^{(1, 3)}$
, Banach’s fixed point theorem together with Lemma 3.3 implies that
![]() $f_{x,z}$
has a unique fixed point in
$f_{x,z}$
has a unique fixed point in
![]() $\Xi _{\varepsilon }^{(2)}$
. This fixed point will be denoted by
$\Xi _{\varepsilon }^{(2)}$
. This fixed point will be denoted by
![]() $g(x, z)$
, i. e.,
$g(x, z)$
, i. e.,
If we plug in
![]() $0$
for
$0$
for
![]() $z$
, we see that (12) holds for
$z$
, we see that (12) holds for
![]() $g(x,0) = 0$
, so uniqueness of the fixed point implies that
$g(x,0) = 0$
, so uniqueness of the fixed point implies that
for
![]() $x\in \Xi _{\varepsilon }^{(1)}$
.
$x\in \Xi _{\varepsilon }^{(1)}$
.
Lemma 3.4.
For sufficiently small
![]() $\varepsilon \gt 0$
,
$\varepsilon \gt 0$
,
![]() $g\colon \Xi _{\varepsilon }^{(1, 3)}\to \Xi _\varepsilon ^{(2)}$
is an analytic function, and
$g\colon \Xi _{\varepsilon }^{(1, 3)}\to \Xi _\varepsilon ^{(2)}$
is an analytic function, and
![]() $\frac{\partial }{\partial z} g(x,z)$
is bounded.
$\frac{\partial }{\partial z} g(x,z)$
is bounded.
Proof. Note that using Lemma 3.2, we have that
![]() $|\frac{\partial }{\partial y}(y-f_{x, z}(y))|=|1-f_{x,z}^{\prime}(y)| \geq 1 - |f_{x,z}^{\prime}(y)| \geq 1 - \lambda$
is bounded away from zero for sufficiently small
$|\frac{\partial }{\partial y}(y-f_{x, z}(y))|=|1-f_{x,z}^{\prime}(y)| \geq 1 - |f_{x,z}^{\prime}(y)| \geq 1 - \lambda$
is bounded away from zero for sufficiently small
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $(x, y, z)\in \Xi _{\varepsilon }$
. Thus the analytic implicit function theorem shows that
$(x, y, z)\in \Xi _{\varepsilon }$
. Thus the analytic implicit function theorem shows that
![]() $g$
as defined by (12) is analytic and has bounded partial derivative
$g$
as defined by (12) is analytic and has bounded partial derivative
![]() $\frac{\partial }{\partial z} g(x,z)$
on
$\frac{\partial }{\partial z} g(x,z)$
on
![]() $\Xi _{\varepsilon }^{(1, 3)}$
for sufficiently small
$\Xi _{\varepsilon }^{(1, 3)}$
for sufficiently small
![]() $\varepsilon \gt 0$
.
$\varepsilon \gt 0$
.
We now intend to solve (10) for
![]() $Y_{h, h}(x)$
. Therefore, we consider the equation
$Y_{h, h}(x)$
. Therefore, we consider the equation
and attempt to solve it for
![]() $z$
. For large
$z$
. For large
![]() $h$
,
$h$
,
![]() $f_{x, z}^{(h-1)}(y)$
will be close to the fixed point
$f_{x, z}^{(h-1)}(y)$
will be close to the fixed point
![]() $g(x, z)$
of
$g(x, z)$
of
![]() $f_{x, z}$
by the Banach fixed point theorem.
$f_{x, z}$
by the Banach fixed point theorem.
Therefore, we define
![]() $\Lambda _h$
as the difference between the two:
$\Lambda _h$
as the difference between the two:
![]() $\Lambda _h(x, y, z)\,{:\!=}\, f_{x,z}^{(h-1)}(y)-g(x, z)$
. So (14) can be rewritten as
$\Lambda _h(x, y, z)\,{:\!=}\, f_{x,z}^{(h-1)}(y)-g(x, z)$
. So (14) can be rewritten as
We first establish bounds on
![]() $\Lambda _h$
.
$\Lambda _h$
.
Lemma 3.5.
For sufficiently small
![]() $\varepsilon \gt 0$
,
$\varepsilon \gt 0$
,
hold uniformly for
![]() $(x, y, z)\in \Xi _{\varepsilon }$
.
$(x, y, z)\in \Xi _{\varepsilon }$
.
Proof. Since
![]() $g$
is defined as the fixed point of
$g$
is defined as the fixed point of
![]() $f_{x, z}$
and
$f_{x, z}$
and
![]() $f_{x, z}$
is a contraction with Lipschitz constant
$f_{x, z}$
is a contraction with Lipschitz constant
![]() $\lambda$
, we have
$\lambda$
, we have
for
![]() $(x, y, z)\in \Xi _\varepsilon$
, so we have shown (16).
$(x, y, z)\in \Xi _\varepsilon$
, so we have shown (16).
For
![]() $(x, y, z)\in \Xi _{\varepsilon/3}$
, Cauchy’s integral formula yields
$(x, y, z)\in \Xi _{\varepsilon/3}$
, Cauchy’s integral formula yields
By (16), we can bound the integral by
![]() $O(\lambda ^h)$
. Thus replacing
$O(\lambda ^h)$
. Thus replacing
![]() $\varepsilon$
by
$\varepsilon$
by
![]() $\varepsilon/3$
yields (17).
$\varepsilon/3$
yields (17).
In order to apply the analytic implicit function theorem to the implicit equation (10) for
![]() $Y_{h,h}$
, we will need to show that the derivative of the difference of the two sides of (15) with respect to
$Y_{h,h}$
, we will need to show that the derivative of the difference of the two sides of (15) with respect to
![]() $z$
is nonzero. The derivative of the second summand on the right-hand side of (15) is small by (17), so we first consider the remaining part of the equation.
$z$
is nonzero. The derivative of the second summand on the right-hand side of (15) is small by (17), so we first consider the remaining part of the equation.
Lemma 3.6.
There is a
![]() $\delta \gt 0$
such that for sufficiently small
$\delta \gt 0$
such that for sufficiently small
![]() $\varepsilon \gt 0$
, we have
$\varepsilon \gt 0$
, we have
for
![]() $(x, z)\in \Xi _{\varepsilon }^{(1, 3)}$
.
$(x, z)\in \Xi _{\varepsilon }^{(1, 3)}$
.
Proof. To compute
![]() $\frac{\partial }{\partial z} g(x, z)$
, we differentiate (12) with respect to
$\frac{\partial }{\partial z} g(x, z)$
, we differentiate (12) with respect to
![]() $z$
and obtain
$z$
and obtain
which leads to
Note that the denominator is nonzero for
![]() $(x, z)\in \Xi _{\varepsilon }^{(1, 3)}$
by Lemma 3.2. We obtain
$(x, z)\in \Xi _{\varepsilon }^{(1, 3)}$
by Lemma 3.2. We obtain
By Lemma 3.4,
![]() $\frac{\partial g(x, z)}{\partial z}$
is analytic and bounded for
$\frac{\partial g(x, z)}{\partial z}$
is analytic and bounded for
![]() $(x, z)\in \Xi _\varepsilon ^{(1, 3)}$
, and by (13), it follows that
$(x, z)\in \Xi _\varepsilon ^{(1, 3)}$
, and by (13), it follows that
for
![]() $\varepsilon \to 0$
, uniformly in
$\varepsilon \to 0$
, uniformly in
![]() $x$
. Therefore, we have
$x$
. Therefore, we have
and
![]() $|{\Phi '(g(x, z))}|= \Phi '(0)+O(\varepsilon )$
for
$|{\Phi '(g(x, z))}|= \Phi '(0)+O(\varepsilon )$
for
![]() $\varepsilon \to 0$
. So (19) yields
$\varepsilon \to 0$
. So (19) yields
for
![]() $\varepsilon \to 0$
. Setting
$\varepsilon \to 0$
. Setting
![]() $\delta \,{:\!=}\, \frac 12 \frac{1}{1+\rho \Phi '(0)}$
and choosing
$\delta \,{:\!=}\, \frac 12 \frac{1}{1+\rho \Phi '(0)}$
and choosing
![]() $\varepsilon$
small enough yields the result.
$\varepsilon$
small enough yields the result.
We need bounds for
![]() $z$
such that we remain in the region where our previous results hold. In fact, (13) shows that
$z$
such that we remain in the region where our previous results hold. In fact, (13) shows that
![]() $z=0$
would be a solution when the summand
$z=0$
would be a solution when the summand
![]() $\Lambda _h$
(which is
$\Lambda _h$
(which is
![]() $O(\lambda ^h)$
) is removed from the implicit equation, so we expect that the summand
$O(\lambda ^h)$
) is removed from the implicit equation, so we expect that the summand
![]() $\Lambda _h$
does not perturb
$\Lambda _h$
does not perturb
![]() $z$
too much. This is shown in the following lemma.
$z$
too much. This is shown in the following lemma.
Lemma 3.7.
Let
![]() $\varepsilon \gt 0$
be sufficiently small and
$\varepsilon \gt 0$
be sufficiently small and
![]() $(x, y, z)\in \Xi _\varepsilon$
such that (15) holds. Then
$(x, y, z)\in \Xi _\varepsilon$
such that (15) holds. Then
Proof. In view of (15) and (16), we have
By definition,
![]() $g(x, z)\in \Xi _{\varepsilon }^{(2)}$
. The implicit equation (12) for
$g(x, z)\in \Xi _{\varepsilon }^{(2)}$
. The implicit equation (12) for
![]() $g(x,z)$
and (21) imply
$g(x,z)$
and (21) imply
Lemma 3.8.
There exists an
![]() $\varepsilon \gt 0$
such that for sufficiently large
$\varepsilon \gt 0$
such that for sufficiently large
![]() $h$
, there is a unique analytic function
$h$
, there is a unique analytic function
![]() $q_h\colon \Xi ^{(1, 2)}_\varepsilon \to{\mathbb{C}}$
such that
$q_h\colon \Xi ^{(1, 2)}_\varepsilon \to{\mathbb{C}}$
such that
and
![]() $q_h(x, 0)=0$
for
$q_h(x, 0)=0$
for
![]() $(x, y)\in \Xi _{\varepsilon }^{(1, 2)}$
; furthermore,
$(x, y)\in \Xi _{\varepsilon }^{(1, 2)}$
; furthermore,
![]() $q_h(x, y)=O(\lambda ^h)$
holds uniformly in
$q_h(x, y)=O(\lambda ^h)$
holds uniformly in
![]() $x$
and
$x$
and
![]() $y$
.
$y$
.
Proof. We choose
![]() $h$
sufficiently large such that (17) implies
$h$
sufficiently large such that (17) implies
for
![]() $(x, y, z)\in \Xi _\varepsilon$
, where
$(x, y, z)\in \Xi _\varepsilon$
, where
![]() $\delta$
is taken as in Lemma 3.6, and such that (20) implies
$\delta$
is taken as in Lemma 3.6, and such that (20) implies
for all
![]() $(x, y, z)\in \Xi _\varepsilon$
for which (15) holds.
$(x, y, z)\in \Xi _\varepsilon$
for which (15) holds.
By definition of
![]() $f$
, we have
$f$
, we have
![]() $f_{x, 0}(0) = 0$
and therefore
$f_{x, 0}(0) = 0$
and therefore
![]() $f_{x, 0}^{(h-1)}(0) = 0$
for every
$f_{x, 0}^{(h-1)}(0) = 0$
for every
![]() $x \in \Xi _\varepsilon ^{(1)}$
, so
$x \in \Xi _\varepsilon ^{(1)}$
, so
![]() $z=0$
is a solution of (14) for
$z=0$
is a solution of (14) for
![]() $y=0$
. By (18) and (23), we have
$y=0$
. By (18) and (23), we have
for
![]() $(x,y,z) \in \Xi _\varepsilon$
. The analytic implicit function theorem thus implies that, for every
$(x,y,z) \in \Xi _\varepsilon$
. The analytic implicit function theorem thus implies that, for every
![]() $x \in \Xi _\varepsilon ^{(1)}$
, there is an analytic function
$x \in \Xi _\varepsilon ^{(1)}$
, there is an analytic function
![]() $q_h$
defined in a neighbourhood of
$q_h$
defined in a neighbourhood of
![]() $(x, 0)$
such that (22) holds there and such that
$(x, 0)$
such that (22) holds there and such that
![]() $q_h(x, 0)=0$
. Next we show that this extends to the whole region
$q_h(x, 0)=0$
. Next we show that this extends to the whole region
![]() $\Xi _\varepsilon ^{(1,2)}$
.
$\Xi _\varepsilon ^{(1,2)}$
.
For
![]() $x_0 \in \Xi _\varepsilon ^{(1)}$
, let
$x_0 \in \Xi _\varepsilon ^{(1)}$
, let
![]() $r(x_0)$
be the supremum of all
$r(x_0)$
be the supremum of all
![]() $r \lt \tau -\rho +\varepsilon$
for which there is an analytic extension of
$r \lt \tau -\rho +\varepsilon$
for which there is an analytic extension of
![]() $y\mapsto q_h(x_0,y)$
from the open disk
$y\mapsto q_h(x_0,y)$
from the open disk
![]() $D_r(0)$
to
$D_r(0)$
to
![]() $\Xi _\varepsilon ^{(3)}$
. Suppose for contradiction that
$\Xi _\varepsilon ^{(3)}$
. Suppose for contradiction that
![]() $r(x_0) \lt \tau - \rho + \varepsilon$
. Consider a point
$r(x_0) \lt \tau - \rho + \varepsilon$
. Consider a point
![]() $y_0$
with
$y_0$
with
![]() $|{y_0}| = r(x_0)$
, and take a sequence
$|{y_0}| = r(x_0)$
, and take a sequence
![]() $y_n \to y_0$
such that
$y_n \to y_0$
such that
![]() $|{y_n}| \lt r(x_0)$
. Note that
$|{y_n}| \lt r(x_0)$
. Note that
![]() $\left |{q_h(x_0,y_n)}\right | \leq \frac{\varepsilon }{2}$
by (24). Without loss of generality, we can assume that
$\left |{q_h(x_0,y_n)}\right | \leq \frac{\varepsilon }{2}$
by (24). Without loss of generality, we can assume that
![]() $q_h(x_0,y_n)$
converges to some
$q_h(x_0,y_n)$
converges to some
![]() $q_0$
with
$q_0$
with
![]() $|{q_0}| \leq \frac{\varepsilon }{2}$
as
$|{q_0}| \leq \frac{\varepsilon }{2}$
as
![]() $n \to \infty$
(by compactness). By continuity, we have
$n \to \infty$
(by compactness). By continuity, we have
![]() $q_0 = f_{x_0, q_0}^{(h-1)}(y_0)$
. Since
$q_0 = f_{x_0, q_0}^{(h-1)}(y_0)$
. Since
![]() $(x_0,y_0,q_0) \in \Xi _\varepsilon$
, we can still use the analytic implicit function theorem together with (25) to conclude that there is a neighbourhood of
$(x_0,y_0,q_0) \in \Xi _\varepsilon$
, we can still use the analytic implicit function theorem together with (25) to conclude that there is a neighbourhood of
![]() $(x_0,y_0,q_0)$
where the equation
$(x_0,y_0,q_0)$
where the equation
![]() $f_{x, z}^{(h-1)}(y) = z$
has exactly one solution
$f_{x, z}^{(h-1)}(y) = z$
has exactly one solution
![]() $z$
for every
$z$
for every
![]() $x$
and
$x$
and
![]() $y$
, and an analytic function
$y$
, and an analytic function
![]() $\tilde{q}_h(x,y)$
such that
$\tilde{q}_h(x,y)$
such that
![]() $\tilde{q}_h(x,y) = f_{x, \tilde{q}_h(x,y)}^{(h-1)}(y)$
and
$\tilde{q}_h(x,y) = f_{x, \tilde{q}_h(x,y)}^{(h-1)}(y)$
and
![]() $\tilde{q}_h(x_0,y_0) = q_0$
. We assume the neighbourhood to be chosen small enough such that
$\tilde{q}_h(x_0,y_0) = q_0$
. We assume the neighbourhood to be chosen small enough such that
![]() $\tilde{q}_h(x, y)\in \Xi _\varepsilon ^{(3)}$
for all
$\tilde{q}_h(x, y)\in \Xi _\varepsilon ^{(3)}$
for all
![]() $(x, y)$
in the neighbourhood. For large enough
$(x, y)$
in the neighbourhood. For large enough
![]() $n$
, this neighbourhood contains
$n$
, this neighbourhood contains
![]() $(x_0,y_n,q_h(x_0,y_n))$
, so we must have
$(x_0,y_n,q_h(x_0,y_n))$
, so we must have
![]() $q_h(x_0,y_n) = \tilde{q}_h(x_0,y_n)$
for all those
$q_h(x_0,y_n) = \tilde{q}_h(x_0,y_n)$
for all those
![]() $n$
. This implies that
$n$
. This implies that
![]() $\tilde{q}_h$
is an analytic continuation of
$\tilde{q}_h$
is an analytic continuation of
![]() $q_h$
in a neighbourhood of
$q_h$
in a neighbourhood of
![]() $(x_0, y_0)$
with values in
$(x_0, y_0)$
with values in
![]() $\Xi _\varepsilon ^{(3)}$
. Since
$\Xi _\varepsilon ^{(3)}$
. Since
![]() $y_0$
was arbitrary, we have reached the desired contradiction.
$y_0$
was arbitrary, we have reached the desired contradiction.
So we conclude that there is indeed such an analytic function
![]() $q_h$
defined on all of
$q_h$
defined on all of
![]() $\Xi _\varepsilon ^{(1,2)}$
, with values in
$\Xi _\varepsilon ^{(1,2)}$
, with values in
![]() $\Xi _\varepsilon ^{(3)}$
. The fact that
$\Xi _\varepsilon ^{(3)}$
. The fact that
![]() $q_h(x,y) = O(\lambda ^h)$
finally follows from Lemma 3.7.
$q_h(x,y) = O(\lambda ^h)$
finally follows from Lemma 3.7.
3.2 Location of the dominant singularity
Let us summarise what has been proven so far. By (10) and Lemma 3.8, for sufficiently large
![]() $h$
we can express
$h$
we can express
![]() $Y_{h,h}$
in terms of
$Y_{h,h}$
in terms of
![]() $Y_{h,1}$
as
$Y_{h,1}$
as
at least in a neighbourhood of
![]() $0$
, which we can plug into (11) to get
$0$
, which we can plug into (11) to get
Setting
this can be rewritten as
The function
![]() $F_h$
is analytic on
$F_h$
is analytic on
![]() $\Xi _\varepsilon ^{(1,2)}$
by Lemma 3.8 and the fact that
$\Xi _\varepsilon ^{(1,2)}$
by Lemma 3.8 and the fact that
![]() $\Phi$
is analytic for these arguments. Note also that
$\Phi$
is analytic for these arguments. Note also that
pointwise for
![]() $(x, y)\in \Xi _{\varepsilon }^{(1, 2)}$
. By the estimate on
$(x, y)\in \Xi _{\varepsilon }^{(1, 2)}$
. By the estimate on
![]() $q_h$
in Lemma 3.8, we also have
$q_h$
in Lemma 3.8, we also have
uniformly for
![]() $(x,y) \in \Xi _\varepsilon ^{(1,2)}$
. Using the same argument as in Lemma 3.5, we can also assume (redefining
$(x,y) \in \Xi _\varepsilon ^{(1,2)}$
. Using the same argument as in Lemma 3.5, we can also assume (redefining
![]() $\varepsilon$
if necessary) that
$\varepsilon$
if necessary) that
and analogous estimates for any finite number of partial derivatives hold as well. Having reduced the original system of equations to a single equation for
![]() $Y_{h,1}(x)$
, we now deduce properties of its dominant singularity. Since
$Y_{h,1}(x)$
, we now deduce properties of its dominant singularity. Since
![]() $Y_{h,1}(x)$
has a power series with nonnegative coefficients, by Pringsheim’s theorem it must have a dominant positive real singularity that we denote by
$Y_{h,1}(x)$
has a power series with nonnegative coefficients, by Pringsheim’s theorem it must have a dominant positive real singularity that we denote by
![]() $\rho _h$
. Since the coefficients of
$\rho _h$
. Since the coefficients of
![]() $Y_{h,1}(x)$
are bounded above by those of
$Y_{h,1}(x)$
are bounded above by those of
![]() $Y(x)$
, we also know that
$Y(x)$
, we also know that
![]() $\rho _h \geq \rho$
.
$\rho _h \geq \rho$
.
Lemma 3.9.
For every sufficiently large
![]() $h$
,
$h$
,
![]() $\rho _h \leq \rho + \lambda ^{h/2}$
. Moreover,
$\rho _h \leq \rho + \lambda ^{h/2}$
. Moreover,
![]() $\eta _{h,1} \,{:\!=}\, Y_{h,1}(\rho _h) = \tau - \rho + O(\lambda ^{h/2})$
.
$\eta _{h,1} \,{:\!=}\, Y_{h,1}(\rho _h) = \tau - \rho + O(\lambda ^{h/2})$
.
Proof. Note first that
![]() $Y_{h,1}(x)$
is an increasing function of
$Y_{h,1}(x)$
is an increasing function of
![]() $x$
for positive real
$x$
for positive real
![]() $x \lt \rho _h$
. Let
$x \lt \rho _h$
. Let
![]() $\tilde{\rho } = \min \!(\rho _h,\rho + \frac{\varepsilon }{2})$
. Suppose first that
$\tilde{\rho } = \min \!(\rho _h,\rho + \frac{\varepsilon }{2})$
. Suppose first that
![]() $\lim _{x \to \tilde{\rho }^-} Y_{h,1}(x) \geq \tau - \rho + \frac{\varepsilon }{2}$
. If
$\lim _{x \to \tilde{\rho }^-} Y_{h,1}(x) \geq \tau - \rho + \frac{\varepsilon }{2}$
. If
![]() $h$
is large enough, this implies together with (27) that
$h$
is large enough, this implies together with (27) that
 \begin{align*} \lim _{x \to \tilde{\rho }^-} \frac{\partial F_h}{\partial y} (x,Y_{h,1}(x)) &= \lim _{x \to \tilde{\rho }^-} \frac{\partial F_{\infty }}{\partial y} (x,Y_{h,1}(x)) + O(\lambda ^h) \\ &\geq \frac{\partial F_{\infty }}{\partial y} \Big (\rho,\tau -\rho + \frac{\varepsilon }{2}\Big ) + O(\lambda ^h) \\ &= \rho \Phi '\Big ( \tau + \frac{\varepsilon }{2}\Big ) + O(\lambda ^h) \gt \rho \Phi '(\tau ) = 1. \end{align*}
\begin{align*} \lim _{x \to \tilde{\rho }^-} \frac{\partial F_h}{\partial y} (x,Y_{h,1}(x)) &= \lim _{x \to \tilde{\rho }^-} \frac{\partial F_{\infty }}{\partial y} (x,Y_{h,1}(x)) + O(\lambda ^h) \\ &\geq \frac{\partial F_{\infty }}{\partial y} \Big (\rho,\tau -\rho + \frac{\varepsilon }{2}\Big ) + O(\lambda ^h) \\ &= \rho \Phi '\Big ( \tau + \frac{\varepsilon }{2}\Big ) + O(\lambda ^h) \gt \rho \Phi '(\tau ) = 1. \end{align*}
On the other hand, we also have
 \begin{align*} \frac{\partial F_h}{\partial y} (\rho/2,Y_{h,1}(\rho/2)) &= \frac{\partial F_{\infty }}{\partial y} (\rho/2,Y_{h,1}(\rho/2)) + O(\lambda ^h) \\ &\leq \frac{\partial F_{\infty }}{\partial y} (\rho/2,Y(\rho/2)-\rho/2) + O(\lambda ^h) \\ &\lt \rho \Phi '(\tau ) = 1, \end{align*}
\begin{align*} \frac{\partial F_h}{\partial y} (\rho/2,Y_{h,1}(\rho/2)) &= \frac{\partial F_{\infty }}{\partial y} (\rho/2,Y_{h,1}(\rho/2)) + O(\lambda ^h) \\ &\leq \frac{\partial F_{\infty }}{\partial y} (\rho/2,Y(\rho/2)-\rho/2) + O(\lambda ^h) \\ &\lt \rho \Phi '(\tau ) = 1, \end{align*}
so by continuity there must exist some
![]() $x_0 \in (\rho/2, \tilde{\rho })$
such that
$x_0 \in (\rho/2, \tilde{\rho })$
such that
Moreover, if
![]() $h$
is large enough we have
$h$
is large enough we have
as
![]() $x_0$
and thus also
$x_0$
and thus also
![]() $Y_{h,1}(x_0)$
are bounded below by positive constants, and analogously
$Y_{h,1}(x_0)$
are bounded below by positive constants, and analogously
![]() $\frac{\partial F_h}{\partial x} (x_0,Y_{h,1}(x_0)) \gt 0$
. But this would mean that
$\frac{\partial F_h}{\partial x} (x_0,Y_{h,1}(x_0)) \gt 0$
. But this would mean that
![]() $Y_{h,1}$
has a square root singularity at
$Y_{h,1}$
has a square root singularity at
![]() $x_0 \lt \rho _h$
(compare the discussion in Section 3.3 later), and we reach a contradiction. Hence we can assume that
$x_0 \lt \rho _h$
(compare the discussion in Section 3.3 later), and we reach a contradiction. Hence we can assume that
Assume next that
![]() $\rho _h \gt \rho + \lambda ^{h/2}$
. Now for
$\rho _h \gt \rho + \lambda ^{h/2}$
. Now for
![]() $x_1 = \rho + \lambda ^{h/2} \lt \tilde{\rho }$
(the inequality holds if
$x_1 = \rho + \lambda ^{h/2} \lt \tilde{\rho }$
(the inequality holds if
![]() $h$
is large enough to make
$h$
is large enough to make
![]() $\lambda ^{h/2} \lt \frac{\varepsilon }{2}$
),
$\lambda ^{h/2} \lt \frac{\varepsilon }{2}$
),
![]() $u_1 = Y_{h,1}(x_1) + x_1$
satisfies
$u_1 = Y_{h,1}(x_1) + x_1$
satisfies
since
![]() $F_h(x,y) = F_{\infty }(x,y) + O(\lambda ^h) = x (\Phi (y+x)-1) + O(\lambda ^h)$
. Note here that
$F_h(x,y) = F_{\infty }(x,y) + O(\lambda ^h) = x (\Phi (y+x)-1) + O(\lambda ^h)$
. Note here that
![]() $u_1 \leq \tau + \frac{\varepsilon }{2} + \lambda ^{h/2}$
by (28), thus
$u_1 \leq \tau + \frac{\varepsilon }{2} + \lambda ^{h/2}$
by (28), thus
![]() $u_1$
is in the region of analyticity of
$u_1$
is in the region of analyticity of
![]() $\Phi$
(again assuming
$\Phi$
(again assuming
![]() $h$
to be large enough). However, since
$h$
to be large enough). However, since
![]() $u \leq \rho \Phi (u)$
for all positive real
$u \leq \rho \Phi (u)$
for all positive real
![]() $u$
for which
$u$
for which
![]() $\Phi (u)$
is well-defined (the line
$\Phi (u)$
is well-defined (the line
![]() $u \mapsto \frac{u}{\rho }$
is a tangent to the graph of the convex function
$u \mapsto \frac{u}{\rho }$
is a tangent to the graph of the convex function
![]() $\Phi$
at
$\Phi$
at
![]() $\tau$
), for sufficiently large
$\tau$
), for sufficiently large
![]() $h$
the right-hand side in (29) is necessarily greater than the left, and we reach another contradiction. So it follows that
$h$
the right-hand side in (29) is necessarily greater than the left, and we reach another contradiction. So it follows that
![]() $\rho _h \leq \rho + \lambda ^{h/2}$
, and in particular
$\rho _h \leq \rho + \lambda ^{h/2}$
, and in particular
![]() $\tilde{\rho } = \rho _h \lt \rho + \frac{\varepsilon }{2}$
if
$\tilde{\rho } = \rho _h \lt \rho + \frac{\varepsilon }{2}$
if
![]() $h$
is large enough. Since we know that
$h$
is large enough. Since we know that
![]() $\lim _{x \to \tilde{\rho }^-} Y_{h,1}(x) \lt \tau - \rho + \frac{\varepsilon }{2}$
, we also have
$\lim _{x \to \tilde{\rho }^-} Y_{h,1}(x) \lt \tau - \rho + \frac{\varepsilon }{2}$
, we also have
![]() $\eta _{h,1} \,{:\!=}\, Y_{h,1}(\rho _h) \lt \tau -\rho + \frac{\varepsilon }{2}$
. We conclude that
$\eta _{h,1} \,{:\!=}\, Y_{h,1}(\rho _h) \lt \tau -\rho + \frac{\varepsilon }{2}$
. We conclude that
![]() $(\rho _h,\eta _{h,1}) \in \Xi _{\varepsilon }^{(1,2)}$
, i.e.,
$(\rho _h,\eta _{h,1}) \in \Xi _{\varepsilon }^{(1,2)}$
, i.e.,
![]() $(\rho _h,\eta _{h,1})$
lies within the region of analyticity of
$(\rho _h,\eta _{h,1})$
lies within the region of analyticity of
![]() $F_h$
. So the singularity at
$F_h$
. So the singularity at
![]() $\rho _h$
must be due to the implicit function theorem failing at this point:
$\rho _h$
must be due to the implicit function theorem failing at this point:
The second equation in particular gives us
by (27). Since
![]() $\Phi '$
is increasing for positive real arguments and we know that
$\Phi '$
is increasing for positive real arguments and we know that
![]() $\rho \Phi '(\tau ) = 1$
and
$\rho \Phi '(\tau ) = 1$
and
![]() $\rho _h = \rho + O(\lambda ^{h/2})$
, we can conclude from this that
$\rho _h = \rho + O(\lambda ^{h/2})$
, we can conclude from this that
![]() $\eta _{h,1} = \tau - \rho + O(\lambda ^{h/2})$
.
$\eta _{h,1} = \tau - \rho + O(\lambda ^{h/2})$
.
As we have established that
![]() $\eta _{h,1} \to \tau - \rho$
as
$\eta _{h,1} \to \tau - \rho$
as
![]() $h \to \infty$
, we will use the abbreviation
$h \to \infty$
, we will use the abbreviation
![]() $\eta _1 \,{:\!=}\, \tau - \rho$
in the following. This will later be generalised to
$\eta _1 \,{:\!=}\, \tau - \rho$
in the following. This will later be generalised to
![]() $\eta _{h,k} \,{:\!=}\, Y_{h,k}(\rho _h) \to \eta _k$
, see Sections 4 and 5. For our next step, we need a multidimensional generalisation of Rouché’s theorem:
$\eta _{h,k} \,{:\!=}\, Y_{h,k}(\rho _h) \to \eta _k$
, see Sections 4 and 5. For our next step, we need a multidimensional generalisation of Rouché’s theorem:
Theorem 3.10 (see [Reference Aizenberg and Yuzhakov1, p. 20, Theorem 2.5]). Let
![]() $\Omega$
be a bounded domain in
$\Omega$
be a bounded domain in
![]() ${\mathbb{C}}^n$
whose boundary
${\mathbb{C}}^n$
whose boundary
![]() $\partial \Omega$
is piecewise smooth. Suppose that
$\partial \Omega$
is piecewise smooth. Suppose that
![]() $u,v\,{:}\, \overline{\Omega } \to{\mathbb{C}}^n$
are analytic functions, and that the boundary of
$u,v\,{:}\, \overline{\Omega } \to{\mathbb{C}}^n$
are analytic functions, and that the boundary of
![]() $\Omega$
does not contain any zeros of
$\Omega$
does not contain any zeros of
![]() $u$
. Moreover, assume that for every
$u$
. Moreover, assume that for every
![]() $z \in \partial \Omega$
, there is at least one coordinate
$z \in \partial \Omega$
, there is at least one coordinate
![]() $j$
for which
$j$
for which
![]() $|{u_j(z)}| \gt |v_j(z)|$
holds. Then
$|{u_j(z)}| \gt |v_j(z)|$
holds. Then
![]() $u$
and
$u$
and
![]() $u+v$
have the same number of zeros in
$u+v$
have the same number of zeros in
![]() $\Omega$
.
$\Omega$
.
Lemma 3.11.
If
![]() $\varepsilon$
is chosen sufficiently small and
$\varepsilon$
is chosen sufficiently small and
![]() $h$
sufficiently large, then the pair
$h$
sufficiently large, then the pair
![]() $(\rho _h,\eta _{h,1})$
is the only solution to the simultaneous equations
$(\rho _h,\eta _{h,1})$
is the only solution to the simultaneous equations
![]() $F_h(x,y) = y$
and
$F_h(x,y) = y$
and
![]() $\frac{\partial }{\partial y}F_h (x,y) = 1$
with
$\frac{\partial }{\partial y}F_h (x,y) = 1$
with
![]() $(x,y) \in \Xi _{\varepsilon }^{(1,2)}$
.
$(x,y) \in \Xi _{\varepsilon }^{(1,2)}$
.
Proof. Note that
![]() $(\rho,\eta _1)$
is a solution to the simultaneous equations
$(\rho,\eta _1)$
is a solution to the simultaneous equations
![]() $F_{\infty }(x,y) = x(\Phi (x+y)\,{-}\,1)\,{=}\,y$
and
$F_{\infty }(x,y) = x(\Phi (x+y)\,{-}\,1)\,{=}\,y$
and
![]() $\frac{\partial }{\partial y}F_{\infty } (x,y) = x \Phi '(x+y) = 1$
, and that there is no other solution with
$\frac{\partial }{\partial y}F_{\infty } (x,y) = x \Phi '(x+y) = 1$
, and that there is no other solution with
![]() $|{x}| \leq \rho + \varepsilon$
and
$|{x}| \leq \rho + \varepsilon$
and
![]() $|{y}| \leq \eta _1 + \varepsilon$
if
$|{y}| \leq \eta _1 + \varepsilon$
if
![]() $\varepsilon$
is chosen sufficiently small by our assumptions on the function
$\varepsilon$
is chosen sufficiently small by our assumptions on the function
![]() $\Phi$
(see Section 2.1). We take
$\Phi$
(see Section 2.1). We take
![]() $\Omega = \Xi _{\varepsilon }^{(1,2)}$
in Theorem 3.10 and set
$\Omega = \Xi _{\varepsilon }^{(1,2)}$
in Theorem 3.10 and set
Moreover, take
Note that both coordinates of
![]() $v$
are
$v$
are
![]() $O(\lambda ^h)$
by (26) and (27). Since the boundary
$O(\lambda ^h)$
by (26) and (27). Since the boundary
![]() $\partial \Omega$
contains no zeros of
$\partial \Omega$
contains no zeros of
![]() $u$
, if we choose
$u$
, if we choose
![]() $h$
sufficiently large, then the conditions of Theorem 3.10 are satisfied. Consequently,
$h$
sufficiently large, then the conditions of Theorem 3.10 are satisfied. Consequently,
![]() $u$
and
$u$
and
![]() $u+v$
have the same number of zeros in
$u+v$
have the same number of zeros in
![]() $\Omega$
, namely
$\Omega$
, namely
![]() $1$
. Solutions to the simultaneous equations
$1$
. Solutions to the simultaneous equations
![]() $F_h(x,y) = y$
and
$F_h(x,y) = y$
and
![]() $\frac{\partial }{\partial y} F_h(x,y) = 1$
are precisely zeros of
$\frac{\partial }{\partial y} F_h(x,y) = 1$
are precisely zeros of
![]() $u+v$
, so this completes the proof.
$u+v$
, so this completes the proof.
At this point, it already follows from general principles (see the discussion in [Reference Flajolet and Sedgewick10, Chapter VII.4]) that for every sufficiently large
![]() $h$
,
$h$
,
![]() $Y_{h,1}$
has a dominant square root singularity at
$Y_{h,1}$
has a dominant square root singularity at
![]() $\rho _h$
, and is otherwise analytic in a domain of the form (6). As we will need uniformity of the asymptotic expansion and a uniform bound for the domain of analyticity, we will make this more precise in the following section.
$\rho _h$
, and is otherwise analytic in a domain of the form (6). As we will need uniformity of the asymptotic expansion and a uniform bound for the domain of analyticity, we will make this more precise in the following section.
3.3 Asymptotic expansion and area of analyticity
Lemma 3.12.
Let
![]() $\varepsilon \gt 0$
be such that all previous lemmata hold. There exist
$\varepsilon \gt 0$
be such that all previous lemmata hold. There exist
![]() $\delta _1, \delta _2 \gt 0$
, some positive number
$\delta _1, \delta _2 \gt 0$
, some positive number
![]() $h_0$
, and analytic functions
$h_0$
, and analytic functions
![]() $R_h$
on
$R_h$
on
![]() $D_{\delta _1}(\rho _h)\times D_{\delta _2}(\eta _{h,1})$
and
$D_{\delta _1}(\rho _h)\times D_{\delta _2}(\eta _{h,1})$
and
![]() $S_h$
on
$S_h$
on
![]() $D_{\delta _2}(\eta _{h,1})$
for
$D_{\delta _2}(\eta _{h,1})$
for
![]() $h\ge h_0$
such that
$h\ge h_0$
such that
![]() $\delta _2\lt \varepsilon$
,
$\delta _2\lt \varepsilon$
,
![]() $D_{\delta _1}(\rho _h)\times D_{\delta _2}(\eta _{h,1})\subseteq \Xi _{\varepsilon }^{(1, 2)}$
and
$D_{\delta _1}(\rho _h)\times D_{\delta _2}(\eta _{h,1})\subseteq \Xi _{\varepsilon }^{(1, 2)}$
and
holds for
![]() $(x, y)\in D_{\delta _1}(\rho _h)\times D_{\delta _2}(\eta _{h,1})$
and
$(x, y)\in D_{\delta _1}(\rho _h)\times D_{\delta _2}(\eta _{h,1})$
and
![]() $h\ge h_0$
and such that
$h\ge h_0$
and such that
![]() $|R_h|$
is bounded from above and below by positive constants on
$|R_h|$
is bounded from above and below by positive constants on
![]() $D_{\delta _1}(\rho _h)\times D_{\delta _2}(\eta _{h,1})$
for
$D_{\delta _1}(\rho _h)\times D_{\delta _2}(\eta _{h,1})$
for
![]() $h\ge h_0$
(uniformly in
$h\ge h_0$
(uniformly in
![]() $h$
) and
$h$
) and
![]() $|S_h|$
is bounded from above and below by positive constants on
$|S_h|$
is bounded from above and below by positive constants on
![]() $D_{\delta _2}(\eta _{h,1})$
for
$D_{\delta _2}(\eta _{h,1})$
for
![]() $h\ge h_0$
(uniformly in
$h\ge h_0$
(uniformly in
![]() $h$
).
$h$
).
Furthermore, the sequences
![]() $R_h$
and
$R_h$
and
![]() $S_h$
converge uniformly to some analytic functions
$S_h$
converge uniformly to some analytic functions
![]() $R$
and
$R$
and
![]() $S$
, respectively. The same holds for their partial derivatives.
$S$
, respectively. The same holds for their partial derivatives.
Proof. Recall that we can approximate partial derivatives of
![]() $F_h$
by those of
$F_h$
by those of
![]() $F_{\infty }$
with an exponential error bound (as in (27)), giving us
$F_{\infty }$
with an exponential error bound (as in (27)), giving us
 \begin{align*} \frac{\partial }{\partial x}F_h(x,y)&=\frac{\partial }{\partial x}F_\infty (x,y) + O(\lambda ^h)\\&= \frac{\partial F_\infty }{\partial x}(\rho, \eta _1) + O(\lambda ^h) + O(x-\rho ) + O(y-\eta _1)\\&=\Phi (\tau ) + O(\lambda ^h)+O(x-\rho ) + O(y-\eta _1), \end{align*}
\begin{align*} \frac{\partial }{\partial x}F_h(x,y)&=\frac{\partial }{\partial x}F_\infty (x,y) + O(\lambda ^h)\\&= \frac{\partial F_\infty }{\partial x}(\rho, \eta _1) + O(\lambda ^h) + O(x-\rho ) + O(y-\eta _1)\\&=\Phi (\tau ) + O(\lambda ^h)+O(x-\rho ) + O(y-\eta _1), \end{align*}
as well as
 \begin{align*} \frac{\partial ^2}{\partial y^2}F_h(x,y)&=\frac{\partial ^2}{\partial y^2}F_\infty (x,y) + O(\lambda ^h)\\ &=\frac{\partial ^2 F_\infty }{\partial y^2}(\rho, \eta _1) + O(\lambda ^h)+ O(x-\rho ) + O(y-\eta _1)&\\ &=\rho \Phi ''(\tau ) + O(\lambda ^h)+ O(x-\rho ) + O(y-\eta _1) \end{align*}
\begin{align*} \frac{\partial ^2}{\partial y^2}F_h(x,y)&=\frac{\partial ^2}{\partial y^2}F_\infty (x,y) + O(\lambda ^h)\\ &=\frac{\partial ^2 F_\infty }{\partial y^2}(\rho, \eta _1) + O(\lambda ^h)+ O(x-\rho ) + O(y-\eta _1)&\\ &=\rho \Phi ''(\tau ) + O(\lambda ^h)+ O(x-\rho ) + O(y-\eta _1) \end{align*}
for
![]() $(x, y)$
in a neighbourhood of
$(x, y)$
in a neighbourhood of
![]() $(\rho, \eta _1)$
contained in
$(\rho, \eta _1)$
contained in
![]() $\Xi _\varepsilon ^{(1, 2)}$
and
$\Xi _\varepsilon ^{(1, 2)}$
and
![]() $h\to \infty$
.
$h\to \infty$
.
Using Lemma 3.9, we choose
![]() $\delta _1\gt 0$
and
$\delta _1\gt 0$
and
![]() $\delta _2\gt 0$
small enough and
$\delta _2\gt 0$
small enough and
![]() $h_0$
large enough such that
$h_0$
large enough such that
![]() $|x-\rho _h|\le \delta _1$
,
$|x-\rho _h|\le \delta _1$
,
![]() $|y-\eta _{h,1}|\le \delta _2$
, and
$|y-\eta _{h,1}|\le \delta _2$
, and
![]() $h\ge h_0$
imply that
$h\ge h_0$
imply that
and
and such that
![]() $\overline{D_{\delta _1}(\rho _h) \times D_{\delta _2}(\eta _{h,1})}\subseteq \Xi _\varepsilon ^{(1, 2)}$
. By Lemma 3.11, we have
$\overline{D_{\delta _1}(\rho _h) \times D_{\delta _2}(\eta _{h,1})}\subseteq \Xi _\varepsilon ^{(1, 2)}$
. By Lemma 3.11, we have
We now define
for
![]() $y\in \overline{D_{\delta _2}(\eta _{h,1})} \setminus \{\eta _{h,1}\}$
. By (33) and (34),
$y\in \overline{D_{\delta _2}(\eta _{h,1})} \setminus \{\eta _{h,1}\}$
. By (33) and (34),
![]() $S_h$
has a removable singularity at
$S_h$
has a removable singularity at
![]() $\eta _{h,1}$
. Therefore it is analytic on
$\eta _{h,1}$
. Therefore it is analytic on
![]() $D_{\delta _2}(\eta _{h,1})$
. By (33), we have
$D_{\delta _2}(\eta _{h,1})$
. By (33), we have
 \begin{align*} F_h(\rho _h, y)-y &= (F_h(\rho _h, y)-y) - (F_h(\rho _h, \eta _{h,1})-\eta _{h,1})\\ &=\int _{\eta _{h,1}}^{y} \Bigl (\frac{\partial }{\partial w}F_h(\rho _h, w)-1\Bigr )\,dw. \end{align*}
\begin{align*} F_h(\rho _h, y)-y &= (F_h(\rho _h, y)-y) - (F_h(\rho _h, \eta _{h,1})-\eta _{h,1})\\ &=\int _{\eta _{h,1}}^{y} \Bigl (\frac{\partial }{\partial w}F_h(\rho _h, w)-1\Bigr )\,dw. \end{align*}
By (34), this can be rewritten as
 \begin{align*} F_h(\rho _h, y)-y &=\int _{\eta _{h,1}}^{y} \Bigl (\Bigl (\frac{\partial F_h}{\partial y}(\rho _h, w)-1\Bigr ) - \Bigl (\frac{\partial F_h}{\partial y}(\rho _h, \eta _{h, 1})-1\Bigr )\Bigr )\,dw\\ &=\int _{\eta _{h,1}}^{y}\int _{\eta _{h, 1}}^w \frac{\partial ^2F_h}{\partial y^2}(\rho _h, v)\,dv\,dw\\ &=\int _{\eta _{h,1}}^{y}\int _{\eta _{h, 1}}^w \rho \Phi ''(\tau )\,dv\,dw+ \int _{\eta _{h,1}}^{y}\int _{\eta _{h, 1}}^w \Bigl (\frac{\partial ^2F_h}{\partial y^2}(\rho _h, v)-\rho \Phi ''(\tau )\Bigr )\,dv\,dw\\ &= \frac 12\rho \Phi ''(\tau )(y-\eta _{h, 1})^2+ \int _{\eta _{h,1}}^{y}\int _{\eta _{h, 1}}^w \Bigl (\frac{\partial ^2F_h}{\partial y^2}(\rho _h, v)-\rho \Phi ''(\tau )\Bigr )\,dv\,dw. \end{align*}
\begin{align*} F_h(\rho _h, y)-y &=\int _{\eta _{h,1}}^{y} \Bigl (\Bigl (\frac{\partial F_h}{\partial y}(\rho _h, w)-1\Bigr ) - \Bigl (\frac{\partial F_h}{\partial y}(\rho _h, \eta _{h, 1})-1\Bigr )\Bigr )\,dw\\ &=\int _{\eta _{h,1}}^{y}\int _{\eta _{h, 1}}^w \frac{\partial ^2F_h}{\partial y^2}(\rho _h, v)\,dv\,dw\\ &=\int _{\eta _{h,1}}^{y}\int _{\eta _{h, 1}}^w \rho \Phi ''(\tau )\,dv\,dw+ \int _{\eta _{h,1}}^{y}\int _{\eta _{h, 1}}^w \Bigl (\frac{\partial ^2F_h}{\partial y^2}(\rho _h, v)-\rho \Phi ''(\tau )\Bigr )\,dv\,dw\\ &= \frac 12\rho \Phi ''(\tau )(y-\eta _{h, 1})^2+ \int _{\eta _{h,1}}^{y}\int _{\eta _{h, 1}}^w \Bigl (\frac{\partial ^2F_h}{\partial y^2}(\rho _h, v)-\rho \Phi ''(\tau )\Bigr )\,dv\,dw. \end{align*}
Rearranging and using the definition of
![]() $S_h(y)$
as well as (32) yields
$S_h(y)$
as well as (32) yields
for all
![]() $y\in \overline{D_{\delta _2}(\eta _{h,1})}$
and
$y\in \overline{D_{\delta _2}(\eta _{h,1})}$
and
![]() $h\ge h_0$
. Thus
$h\ge h_0$
. Thus
![]() $|{S_h(y)}|$
is bounded from below and above by positive constants for every such
$|{S_h(y)}|$
is bounded from below and above by positive constants for every such
![]() $y$
and
$y$
and
![]() $h$
.
$h$
.
We now define
![]() $R_h(x, y)$
such that (30) holds, which is equivalent to
$R_h(x, y)$
such that (30) holds, which is equivalent to
for
![]() $x\in \overline{D_{\delta _1}(\rho _h)}\setminus \{\rho _h\}$
and
$x\in \overline{D_{\delta _1}(\rho _h)}\setminus \{\rho _h\}$
and
![]() $y\in \overline{D_{\delta _2}(\eta _{h,1})}$
. We have
$y\in \overline{D_{\delta _2}(\eta _{h,1})}$
. We have
 \begin{align*} F_h(\rho _h, y)-F_h(x,y)&=\int _x^{\rho _h}\frac{\partial F_h}{\partial x}(w, y)\,dw\\ &=\Phi (\tau )(\rho _h-x)+\int _x^{\rho _h}\Bigl (\frac{\partial F_h}{\partial x}(w, y)-\Phi (\tau )\Bigr )\,dw. \end{align*}
\begin{align*} F_h(\rho _h, y)-F_h(x,y)&=\int _x^{\rho _h}\frac{\partial F_h}{\partial x}(w, y)\,dw\\ &=\Phi (\tau )(\rho _h-x)+\int _x^{\rho _h}\Bigl (\frac{\partial F_h}{\partial x}(w, y)-\Phi (\tau )\Bigr )\,dw. \end{align*}
Rearranging and using the definition of
![]() $R_h(x, y)$
yields
$R_h(x, y)$
yields
by (31) for
![]() $x\in \overline{D_{\delta _1}(\rho _h)}\setminus \{\rho _h\}$
and
$x\in \overline{D_{\delta _1}(\rho _h)}\setminus \{\rho _h\}$
and
![]() $y\in \overline{D_{\delta _2}(\eta _{h,1})}$
and
$y\in \overline{D_{\delta _2}(\eta _{h,1})}$
and
![]() $h\ge h_0$
. In other words,
$h\ge h_0$
. In other words,
![]() $|{R_h(x,y)}|$
is bounded from below and above by positive constants for these
$|{R_h(x,y)}|$
is bounded from below and above by positive constants for these
![]() $(x, y)$
and
$(x, y)$
and
![]() $h$
.
$h$
.
To prove analyticity of
![]() $R_h$
, we use Cauchy’s formula to rewrite it as
$R_h$
, we use Cauchy’s formula to rewrite it as
for
![]() $x \neq \rho _h$
(note that the integrand has a removable singularity at
$x \neq \rho _h$
(note that the integrand has a removable singularity at
![]() $\zeta =\rho _h$
in this case). The integral is also defined for
$\zeta =\rho _h$
in this case). The integral is also defined for
![]() $x=\rho _h$
and clearly defines an analytic function on
$x=\rho _h$
and clearly defines an analytic function on
![]() $D_{\delta _1}(\rho _h)\times D_{\delta _2}(\eta _{h,1})$
whose absolute value is bounded from above and below by a constant.
$D_{\delta _1}(\rho _h)\times D_{\delta _2}(\eta _{h,1})$
whose absolute value is bounded from above and below by a constant.
To see uniform convergence of
![]() $R_h$
, we use Cauchy’s formula once more and get
$R_h$
, we use Cauchy’s formula once more and get
for
![]() $x\in D_{\delta _1}(\rho _h)$
and
$x\in D_{\delta _1}(\rho _h)$
and
![]() $y\in D_{\delta _2}(\eta _{h,1})$
. Without loss of generality,
$y\in D_{\delta _2}(\eta _{h,1})$
. Without loss of generality,
![]() $h_0$
is large enough such that
$h_0$
is large enough such that
![]() $|{\rho _h-\rho }|\lt \delta _1/4$
and
$|{\rho _h-\rho }|\lt \delta _1/4$
and
![]() $|{\eta _{h,1}-\eta _1}|\lt \delta _2/4$
. By Cauchy’s theorem, we can change the contour of integration such that (35) implies
$|{\eta _{h,1}-\eta _1}|\lt \delta _2/4$
. By Cauchy’s theorem, we can change the contour of integration such that (35) implies
for
![]() $x\in D_{\delta _1/4}(\rho )$
and
$x\in D_{\delta _1/4}(\rho )$
and
![]() $y\in D_{\delta _2/4}(\eta _{1})$
, as the deformation is happening within the region of analyticity of the integrand. Using (26) and the fact that the denominator of the integrand is bounded away from zero shows that
$y\in D_{\delta _2/4}(\eta _{1})$
, as the deformation is happening within the region of analyticity of the integrand. Using (26) and the fact that the denominator of the integrand is bounded away from zero shows that
for
![]() $x\in D_{\delta _1/4}(\rho )$
and
$x\in D_{\delta _1/4}(\rho )$
and
![]() $y\in D_{\delta _2/4}(\eta _{1})$
. By Lemma 3.9, replacing the remaining occurrences of
$y\in D_{\delta _2/4}(\eta _{1})$
. By Lemma 3.9, replacing the remaining occurrences of
![]() $\rho _h$
by
$\rho _h$
by
![]() $\rho$
induces another error term of
$\rho$
induces another error term of
![]() $O(\lambda ^{h/2})$
, so that we get
$O(\lambda ^{h/2})$
, so that we get
with
for
![]() $x\in D_{\delta _1/4}(\rho )$
and
$x\in D_{\delta _1/4}(\rho )$
and
![]() $y\in D_{\delta _2/4}(\eta _{1})$
. Of course, the
$y\in D_{\delta _2/4}(\eta _{1})$
. Of course, the
![]() $O$
constants do not depend on
$O$
constants do not depend on
![]() $x$
and
$x$
and
![]() $y$
; therefore, we have uniform convergence. Analogously, we get
$y$
; therefore, we have uniform convergence. Analogously, we get
with
for
![]() $y\in D_{\delta _2/4}(\eta _{1})$
. Analogous results hold for partial derivatives.
$y\in D_{\delta _2/4}(\eta _{1})$
. Analogous results hold for partial derivatives.
We replace
![]() $\delta _1$
by
$\delta _1$
by
![]() $\delta _1/4$
and
$\delta _1/4$
and
![]() $\delta _2$
by
$\delta _2$
by
![]() $\delta _2/4$
to get the result as stated in the lemma.
$\delta _2/4$
to get the result as stated in the lemma.
Lemma 3.13.
The constants
![]() $\delta _1$
,
$\delta _1$
,
![]() $\delta _2$
and
$\delta _2$
and
![]() $h_0$
in Lemma 3.12 can be chosen such that whenever
$h_0$
in Lemma 3.12 can be chosen such that whenever
![]() $y=F_h(x, y)$
for some
$y=F_h(x, y)$
for some
![]() $(x, y)\in D_{\delta _1}(\rho _h)\times D_{\delta _2}(\eta _{h,1})$
and some
$(x, y)\in D_{\delta _1}(\rho _h)\times D_{\delta _2}(\eta _{h,1})$
and some
![]() $h\ge h_0$
, we have
$h\ge h_0$
, we have
![]() $|{y-\eta _{h,1}}|\lt \delta _2/2$
.
$|{y-\eta _{h,1}}|\lt \delta _2/2$
.
Proof. We first choose
![]() $\delta _1$
and
$\delta _1$
and
![]() $\delta _2$
as in Lemma 3.12. Then
$\delta _2$
as in Lemma 3.12. Then
![]() $y=F_h(x,y)$
and Lemma 3.12 imply that
$y=F_h(x,y)$
and Lemma 3.12 imply that
 \begin{equation*} |{y-\eta _{h,1}}|=\sqrt {|{x-\rho _h}|\left |{\frac {R_h(x, y)}{S_h(y)}}\right |}. \end{equation*}
\begin{equation*} |{y-\eta _{h,1}}|=\sqrt {|{x-\rho _h}|\left |{\frac {R_h(x, y)}{S_h(y)}}\right |}. \end{equation*}
The fraction on the right-hand side is bounded by some absolute constant according to Lemma 3.12. So by decreasing
![]() $\delta _1$
if necessary, the right-hand side is at most
$\delta _1$
if necessary, the right-hand side is at most
![]() $\delta _2/2$
.
$\delta _2/2$
.
Lemma 3.14.
Let
![]() $\varepsilon \gt 0$
be such that the previous lemmata hold. There exists
$\varepsilon \gt 0$
be such that the previous lemmata hold. There exists
![]() $\delta _0 \gt 0$
such that, for all sufficiently large
$\delta _0 \gt 0$
such that, for all sufficiently large
![]() $h$
, the asymptotic formula
$h$
, the asymptotic formula
holds for
![]() $x\in D_{\delta _0}(\rho _h)$
with
$x\in D_{\delta _0}(\rho _h)$
with
![]() $|{\mathrm{Arg}(x-\rho _h)}|\ge \pi/4$
and certain sequences
$|{\mathrm{Arg}(x-\rho _h)}|\ge \pi/4$
and certain sequences
![]() $a_h$
,
$a_h$
,
![]() $b_h$
and
$b_h$
and
![]() $c_h$
. The
$c_h$
. The
![]() $O$
-constant is independent of
$O$
-constant is independent of
![]() $h$
, and
$h$
, and
![]() $a_h$
,
$a_h$
,
![]() $b_h$
,
$b_h$
,
![]() $c_h$
converge to the coefficients
$c_h$
converge to the coefficients
![]() $a$
,
$a$
,
![]() $b$
,
$b$
,
![]() $c$
in (4) at an exponential rate as
$c$
in (4) at an exponential rate as
![]() $h \to \infty$
. Additionally,
$h \to \infty$
. Additionally,
![]() $|{Y_{h,1}(x)-\eta _1}|\lt \varepsilon/2$
for all these
$|{Y_{h,1}(x)-\eta _1}|\lt \varepsilon/2$
for all these
![]() $x$
.
$x$
.
Proof. By (30), the function
![]() $Y_{h,1}$
is determined by the implicit equation
$Y_{h,1}$
is determined by the implicit equation
For
![]() $r\gt 0$
, set
$r\gt 0$
, set
![]() $C(r)\,{:\!=}\, \{x\in D_r(\rho _h)\colon |{\mathrm{Arg}(x-\rho _h)}|\ge \pi/4\}$
and
$C(r)\,{:\!=}\, \{x\in D_r(\rho _h)\colon |{\mathrm{Arg}(x-\rho _h)}|\ge \pi/4\}$
and
![]() $\widetilde{C}(r)\,{:\!=}\, \{x\in{\mathbb{C}}\colon |{x-\rho _h}|\,{=}\,r \text{ and } |{\mathrm{Arg}(x-\rho _h)}|\ge \pi/4\}$
. Choose
$\widetilde{C}(r)\,{:\!=}\, \{x\in{\mathbb{C}}\colon |{x-\rho _h}|\,{=}\,r \text{ and } |{\mathrm{Arg}(x-\rho _h)}|\ge \pi/4\}$
. Choose
![]() $\delta _1$
,
$\delta _1$
,
![]() $\delta _2$
,
$\delta _2$
,
![]() $h_0$
as in Lemma 3.13. For some
$h_0$
as in Lemma 3.13. For some
![]() $h\ge h_0$
, let
$h\ge h_0$
, let
![]() $r_h$
be the supremum of all
$r_h$
be the supremum of all
![]() $r\le \delta _1$
such that
$r\le \delta _1$
such that
![]() $Y_{h,1}$
can be continued analytically to
$Y_{h,1}$
can be continued analytically to
![]() $C(r)$
with values in
$C(r)$
with values in
![]() $D_{\delta _2/2}(\eta _{h,1})$
. We claim that
$D_{\delta _2/2}(\eta _{h,1})$
. We claim that
![]() $r_h=\delta _1$
.
$r_h=\delta _1$
.
Suppose for contradiction that
![]() $r_h\lt \delta _1$
and let
$r_h\lt \delta _1$
and let
![]() $x_{\infty }\in \widetilde C(r_h)$
. Choose a sequence of elements
$x_{\infty }\in \widetilde C(r_h)$
. Choose a sequence of elements
![]() $x_n\in C(r_h)$
converging to
$x_n\in C(r_h)$
converging to
![]() $x_\infty$
for
$x_\infty$
for
![]() $n\to \infty$
and set
$n\to \infty$
and set
![]() $y_n\,{:\!=}\, Y_{h, 1}(x_n)$
for all
$y_n\,{:\!=}\, Y_{h, 1}(x_n)$
for all
![]() $n$
. By assumption, we have
$n$
. By assumption, we have
![]() $|{y_n-\eta _{h,1}}|\le \delta _2/2$
. By replacing the sequence
$|{y_n-\eta _{h,1}}|\le \delta _2/2$
. By replacing the sequence
![]() $x_n$
by a subsequence if necessary, we may assume that the sequence
$x_n$
by a subsequence if necessary, we may assume that the sequence
![]() $y_n$
is convergent to some limit
$y_n$
is convergent to some limit
![]() $y_{\infty }$
. Note that
$y_{\infty }$
. Note that
![]() $|{y_\infty -\eta _{h,1}}|\le \delta _2/2$
. By continuity of
$|{y_\infty -\eta _{h,1}}|\le \delta _2/2$
. By continuity of
![]() $F_h$
, we also have
$F_h$
, we also have
![]() $y_\infty =F_h(x_\infty, y_\infty )$
. As
$y_\infty =F_h(x_\infty, y_\infty )$
. As
![]() $(x_\infty, y_\infty )\in \Xi _\varepsilon ^{(1, 2)}$
with
$(x_\infty, y_\infty )\in \Xi _\varepsilon ^{(1, 2)}$
with
![]() $x_\infty \neq \rho _h$
, Lemma 3.11 and the analytic implicit function theorem imply that
$x_\infty \neq \rho _h$
, Lemma 3.11 and the analytic implicit function theorem imply that
![]() $Y_{h,1}$
can be continued analytically in a suitable open neighbourhood of
$Y_{h,1}$
can be continued analytically in a suitable open neighbourhood of
![]() $x_\infty$
. This neighbourhood can be chosen small enough such that the inequality
$x_\infty$
. This neighbourhood can be chosen small enough such that the inequality
![]() $|{Y_{h,1}(x)-\eta _{h,1}}|\le \delta _2$
holds for all
$|{Y_{h,1}(x)-\eta _{h,1}}|\le \delta _2$
holds for all
![]() $x$
in this neighbourhood. However, Lemma 3.13 implies that we then actually have
$x$
in this neighbourhood. However, Lemma 3.13 implies that we then actually have
![]() $|{Y_{h,1}(x)-\eta _{h,1}}|\le \delta _2/2$
for all such
$|{Y_{h,1}(x)-\eta _{h,1}}|\le \delta _2/2$
for all such
![]() $x$
.
$x$
.
The set of these open neighbourhoods associated with all
![]() $x_\infty \in \widetilde{C}(r_h)$
covers the compact set
$x_\infty \in \widetilde{C}(r_h)$
covers the compact set
![]() $\widetilde{C}(r_h)$
, so a finite subset of these open neighbourhoods can be selected. Thus we find an analytic continuation of
$\widetilde{C}(r_h)$
, so a finite subset of these open neighbourhoods can be selected. Thus we find an analytic continuation of
![]() $Y_{h,1}$
to
$Y_{h,1}$
to
![]() $C(\widetilde{r}_h)$
for some
$C(\widetilde{r}_h)$
for some
![]() $\widetilde{r}_h\in (r_h, \delta _1)$
with values still in
$\widetilde{r}_h\in (r_h, \delta _1)$
with values still in
![]() $D_{\delta _2/2}(\eta _{h,1})$
, which is a contradiction to the choice of
$D_{\delta _2/2}(\eta _{h,1})$
, which is a contradiction to the choice of
![]() $r_h$
.
$r_h$
.
Thus we have
![]() $r_h=\delta _1$
. In particular, choosing
$r_h=\delta _1$
. In particular, choosing
![]() $h$
large enough that
$h$
large enough that
![]() $|{\eta _{h, 1} - \eta _1}| \lt (\varepsilon - \delta _2)/2$
gives
$|{\eta _{h, 1} - \eta _1}| \lt (\varepsilon - \delta _2)/2$
gives
![]() $|{Y_{h,1}(x)-\eta _1}| \le |{Y_{h,1}(x) - \eta _{h,1}}| + |{\eta _{h,1}-\eta _1}| \lt \delta _2/2 + (\varepsilon -\delta _2)/2 = \varepsilon/2$
for all
$|{Y_{h,1}(x)-\eta _1}| \le |{Y_{h,1}(x) - \eta _{h,1}}| + |{\eta _{h,1}-\eta _1}| \lt \delta _2/2 + (\varepsilon -\delta _2)/2 = \varepsilon/2$
for all
![]() $x\in C(\delta _1)$
.
$x\in C(\delta _1)$
.
Rearranging (39) yields
We know from Lemma 3.12 that
![]() $R_h$
is bounded above and
$R_h$
is bounded above and
![]() $S_h$
is bounded below on
$S_h$
is bounded below on
![]() $D_{\delta _1}(\rho _h)\times D_{\delta _2}(\eta _{h,1})$
and
$D_{\delta _1}(\rho _h)\times D_{\delta _2}(\eta _{h,1})$
and
![]() $D_{\delta _2}(\eta _{h,1})$
, respectively. Therefore, the absolute value of the first factor on the right-hand side of (40) is bounded above and below by positive constants for
$D_{\delta _2}(\eta _{h,1})$
, respectively. Therefore, the absolute value of the first factor on the right-hand side of (40) is bounded above and below by positive constants for
![]() $x\in D_{\delta _1}(\rho _h)$
. For
$x\in D_{\delta _1}(\rho _h)$
. For
![]() $x\lt \rho _h$
, we have that the factor
$x\lt \rho _h$
, we have that the factor
![]() $(1-x/\rho _h)$
is trivially positive and that
$(1-x/\rho _h)$
is trivially positive and that
![]() $\eta _{h,1}\gt Y_{h,1}(x)$
because
$\eta _{h,1}\gt Y_{h,1}(x)$
because
![]() $Y_{h,1}$
is strictly increasing on
$Y_{h,1}$
is strictly increasing on
![]() $(0, \rho _h)$
, so the first factor on the right-hand side of (40) must be positive. Thus we may take the principal value of the square root to rewrite (40) as
$(0, \rho _h)$
, so the first factor on the right-hand side of (40) must be positive. Thus we may take the principal value of the square root to rewrite (40) as
 \begin{equation} \eta _{h, 1} - Y_{h,1}(x) = \sqrt{\rho _h\frac{R_h(x, Y_{h,1}(x))}{S_h(Y_{h, 1}(x))}} \Bigl (1-\frac{x}{\rho _h}\Bigr )^{1/2} \end{equation}
\begin{equation} \eta _{h, 1} - Y_{h,1}(x) = \sqrt{\rho _h\frac{R_h(x, Y_{h,1}(x))}{S_h(Y_{h, 1}(x))}} \Bigl (1-\frac{x}{\rho _h}\Bigr )^{1/2} \end{equation}
for
![]() $x\in C(\delta _1)$
. The above considerations also show that the radicand in (41) remains positive in the limit
$x\in C(\delta _1)$
. The above considerations also show that the radicand in (41) remains positive in the limit
![]() $x\to \rho _h^{-}$
(i.e., as
$x\to \rho _h^{-}$
(i.e., as
![]() $x$
approaches
$x$
approaches
![]() $\rho _h$
from the left) and then for
$\rho _h$
from the left) and then for
![]() $h\to \infty$
.
$h\to \infty$
.
As we just observed that the first factor on the right-hand side of (41) is bounded, (41) implies
with an
![]() $O$
-constant that is independent of
$O$
-constant that is independent of
![]() $h$
. We can now iterate this argument: using Taylor expansion along with the fact that partial derivatives of
$h$
. We can now iterate this argument: using Taylor expansion along with the fact that partial derivatives of
![]() $R_h$
and
$R_h$
and
![]() $S_h$
are uniformly bounded above while
$S_h$
are uniformly bounded above while
![]() $S_h$
is also uniformly bounded below, we obtain
$S_h$
is also uniformly bounded below, we obtain
 \begin{align*} \frac{R_h(x, Y_{h,1}(x))}{S_h(Y_{h, 1}(x))} &= \frac{R_h(\rho _h,\eta _{h,1}) + O(x-\rho _h) + O(Y_{h,1}(x)-\eta _{h,1})}{S_h(\eta _{h,1}) + O(Y_{h,1}(x)-\eta _{h,1})} \\&= \frac{R_h(\rho _h,\eta _{h,1})}{S_h(\eta _{h,1})} + O\bigl ((x-\rho _h)^{1/2}\bigr ). \end{align*}
\begin{align*} \frac{R_h(x, Y_{h,1}(x))}{S_h(Y_{h, 1}(x))} &= \frac{R_h(\rho _h,\eta _{h,1}) + O(x-\rho _h) + O(Y_{h,1}(x)-\eta _{h,1})}{S_h(\eta _{h,1}) + O(Y_{h,1}(x)-\eta _{h,1})} \\&= \frac{R_h(\rho _h,\eta _{h,1})}{S_h(\eta _{h,1})} + O\bigl ((x-\rho _h)^{1/2}\bigr ). \end{align*}
Plugging this into (41) yields
 \begin{equation*} \eta _{h, 1} - Y_{h,1}(x) = \sqrt {\rho _h\frac {R_h(\rho _h, \eta _{h,1})}{S_h(\eta _{h,1})}} \Bigl (1-\frac {x}{\rho _h}\Bigr )^{1/2} + O( x - \rho _h), \end{equation*}
\begin{equation*} \eta _{h, 1} - Y_{h,1}(x) = \sqrt {\rho _h\frac {R_h(\rho _h, \eta _{h,1})}{S_h(\eta _{h,1})}} \Bigl (1-\frac {x}{\rho _h}\Bigr )^{1/2} + O( x - \rho _h), \end{equation*}
still with an
![]() $O$
-constant that is independent of
$O$
-constant that is independent of
![]() $h$
. This can be continued arbitrarily often to obtain further terms of the expansion and an improved error term (for our purposes, it is enough to stop at
$h$
. This can be continued arbitrarily often to obtain further terms of the expansion and an improved error term (for our purposes, it is enough to stop at
![]() $O((x - \rho _h)^2)$
). Indeed it is well known (cf. [Reference Flajolet and Sedgewick10, Lemma VII.3]) that an implicit equation of the form (39) has a solution as a power series in
$O((x - \rho _h)^2)$
). Indeed it is well known (cf. [Reference Flajolet and Sedgewick10, Lemma VII.3]) that an implicit equation of the form (39) has a solution as a power series in
![]() $(1-x/\rho _h)^{1/2}$
. In particular, (38) follows with an error term that is uniform in
$(1-x/\rho _h)^{1/2}$
. In particular, (38) follows with an error term that is uniform in
![]() $h$
. The coefficients
$h$
. The coefficients
![]() $a_h,b_h,c_h$
can be expressed in terms of
$a_h,b_h,c_h$
can be expressed in terms of
![]() $R_h$
,
$R_h$
,
![]() $S_h$
and their partial derivatives evaluated at
$S_h$
and their partial derivatives evaluated at
![]() $(\rho _h,\eta _{h,1})$
: specifically,
$(\rho _h,\eta _{h,1})$
: specifically,
 \begin{align*} a_h &= - \sqrt{\rho _h\frac{R_h(\rho _h, \eta _{h,1})}{S_h(\eta _{h,1})}},\\ b_h &= \frac{\rho _h S_h(\eta _{h,1}) \frac{\partial R_h}{\partial y}(\rho _h,\eta _{h,1})-\rho _h S_h^{\prime}(\eta _{h,1}) R_h(\rho _h,\eta _{h,1})}{2 S_h(\eta _{h,1})^2},\\ c_h &=\frac{\rho _h^{3/2}N}{8\sqrt{R_h(\rho _h, \eta _{h,1})S_h(\eta _{h,1})^7}}, \end{align*}
\begin{align*} a_h &= - \sqrt{\rho _h\frac{R_h(\rho _h, \eta _{h,1})}{S_h(\eta _{h,1})}},\\ b_h &= \frac{\rho _h S_h(\eta _{h,1}) \frac{\partial R_h}{\partial y}(\rho _h,\eta _{h,1})-\rho _h S_h^{\prime}(\eta _{h,1}) R_h(\rho _h,\eta _{h,1})}{2 S_h(\eta _{h,1})^2},\\ c_h &=\frac{\rho _h^{3/2}N}{8\sqrt{R_h(\rho _h, \eta _{h,1})S_h(\eta _{h,1})^7}}, \end{align*}
where the numerator
![]() $N$
is a polynomial in
$N$
is a polynomial in
![]() $R_h(\rho _h,\eta _{h,1})$
,
$R_h(\rho _h,\eta _{h,1})$
,
![]() $S_h(\eta _{h,1})$
and their derivatives. By Lemma 3.12,
$S_h(\eta _{h,1})$
and their derivatives. By Lemma 3.12,
![]() $R_h$
and
$R_h$
and
![]() $S_h$
as well as their partial derivatives converge uniformly to
$S_h$
as well as their partial derivatives converge uniformly to
![]() $R$
and
$R$
and
![]() $S$
as well as their partial derivatives, respectively, with an error bound of
$S$
as well as their partial derivatives, respectively, with an error bound of
![]() $O(\lambda ^{h/2})$
. We also know that
$O(\lambda ^{h/2})$
. We also know that
![]() $\rho _h$
and
$\rho _h$
and
![]() $\eta _{h,1}$
converge exponentially to
$\eta _{h,1}$
converge exponentially to
![]() $\rho$
and
$\rho$
and
![]() $\eta _1$
, respectively, see Lemma 3.9. This means that first replacing all occurrences of
$\eta _1$
, respectively, see Lemma 3.9. This means that first replacing all occurrences of
![]() $R_h$
and
$R_h$
and
![]() $S_h$
by
$S_h$
by
![]() $R$
and
$R$
and
![]() $S$
, respectively, and then replacing all occurrences of
$S$
, respectively, and then replacing all occurrences of
![]() $\rho _h$
and
$\rho _h$
and
![]() $\eta _{h,1}$
by
$\eta _{h,1}$
by
![]() $\rho$
and
$\rho$
and
![]() $\eta _1$
, respectively, shows that
$\eta _1$
, respectively, shows that
![]() $a_h=a+O(\lambda ^{h/2})$
,
$a_h=a+O(\lambda ^{h/2})$
,
![]() $b_h=b+O(\lambda ^{h/2})$
, and
$b_h=b+O(\lambda ^{h/2})$
, and
![]() $c_h=c+O(\lambda ^{h/2})$
where
$c_h=c+O(\lambda ^{h/2})$
where
![]() $a$
,
$a$
,
![]() $b$
, and
$b$
, and
![]() $c$
are the results of these replacements. Taking the limit for
$c$
are the results of these replacements. Taking the limit for
![]() $h\to \infty$
in (30) shows that
$h\to \infty$
in (30) shows that
![]() $R$
and
$R$
and
![]() $S$
and therefore
$S$
and therefore
![]() $a$
,
$a$
,
![]() $b$
, and
$b$
, and
![]() $c$
play the same role with respect to
$c$
play the same role with respect to
![]() $F_\infty$
as
$F_\infty$
as
![]() $R_h$
,
$R_h$
,
![]() $S_h$
,
$S_h$
,
![]() $a_h$
,
$a_h$
,
![]() $b_h$
, and
$b_h$
, and
![]() $c_h$
play with respect to
$c_h$
play with respect to
![]() $F_h$
, which implies that
$F_h$
, which implies that
![]() $a$
,
$a$
,
![]() $b$
, and
$b$
, and
![]() $c$
are indeed the constants from (4).
$c$
are indeed the constants from (4).
Having dealt with the behaviour around the singularity, it remains to prove a uniform bound on
![]() $Y_{h,1}$
in a domain of the form (6) for fixed
$Y_{h,1}$
in a domain of the form (6) for fixed
![]() $\delta$
.
$\delta$
.
Lemma 3.15.
Let
![]() $\varepsilon \gt 0$
be such that all previous lemmata hold. There exist
$\varepsilon \gt 0$
be such that all previous lemmata hold. There exist
![]() $\delta \gt 0$
and a positive integer
$\delta \gt 0$
and a positive integer
![]() $h_0$
such that
$h_0$
such that
![]() $Y_{h,1}(x)$
has an analytic continuation to the domain
$Y_{h,1}(x)$
has an analytic continuation to the domain
for all
![]() $h \geq h_0$
, and has the uniform upper bound
$h \geq h_0$
, and has the uniform upper bound
for all
![]() $h \geq h_0$
and all
$h \geq h_0$
and all
![]() $x$
.
$x$
.
Proof. Let us define
![]() $r_h = \sup \mathcal{R}_h$
, where
$r_h = \sup \mathcal{R}_h$
, where
with
![]() $\delta _0$
as in the previous lemma. Note that trivially,
$\delta _0$
as in the previous lemma. Note that trivially,
![]() $r_h \geq \rho$
. If
$r_h \geq \rho$
. If
![]() $\liminf _{h \to \infty } r_h \gt \rho$
, we are done: in this case, there is some
$\liminf _{h \to \infty } r_h \gt \rho$
, we are done: in this case, there is some
![]() $\delta \gt 0$
such that
$\delta \gt 0$
such that
![]() $Y_{h,1}$
extends analytically to
$Y_{h,1}$
extends analytically to
![]() $D_{\rho (1+\delta )}(0) \setminus D_{\delta _0}(\rho _h)$
and satisfies
$D_{\rho (1+\delta )}(0) \setminus D_{\delta _0}(\rho _h)$
and satisfies
![]() $|Y_{h,1}(x)| \lt \eta _1 + \frac{\varepsilon }{2}$
there. As the previous lemma covers
$|Y_{h,1}(x)| \lt \eta _1 + \frac{\varepsilon }{2}$
there. As the previous lemma covers
![]() $D_{\delta _0}(\rho _h)$
, this already completes the proof.
$D_{\delta _0}(\rho _h)$
, this already completes the proof.
So let us assume that
![]() $\liminf _{h \to \infty } r_h = \rho$
and derive a contradiction. The assumption implies that there is an increasing sequence of positive integers
$\liminf _{h \to \infty } r_h = \rho$
and derive a contradiction. The assumption implies that there is an increasing sequence of positive integers
![]() $h_j$
such that
$h_j$
such that
![]() $\lim _{j\to \infty }r_{h_j}=\rho$
. Without loss of generality, we may assume that
$\lim _{j\to \infty }r_{h_j}=\rho$
. Without loss of generality, we may assume that
![]() $r_{h_j} \leq \rho + \frac{\varepsilon }{2}$
for all
$r_{h_j} \leq \rho + \frac{\varepsilon }{2}$
for all
![]() $j$
. Pick (for each sufficiently large
$j$
. Pick (for each sufficiently large
![]() $j$
) a point
$j$
) a point
![]() $x_{h_j}$
with
$x_{h_j}$
with
![]() $|x_{h_j}| = r_{h_j}$
and
$|x_{h_j}| = r_{h_j}$
and
![]() $|Y_{{h_j},1}(x_{h_j})| = \eta _1 + \frac{\varepsilon }{2}$
. If this were not possible, we could analytically continue
$|Y_{{h_j},1}(x_{h_j})| = \eta _1 + \frac{\varepsilon }{2}$
. If this were not possible, we could analytically continue
![]() $Y_{{h_j},1}$
at every point
$Y_{{h_j},1}$
at every point
![]() $x$
with
$x$
with
![]() $|{x}| = r_{h_j}$
and
$|{x}| = r_{h_j}$
and
![]() $x \notin D_{\delta _0}(\rho _{h_j})$
to a disk where
$x \notin D_{\delta _0}(\rho _{h_j})$
to a disk where
![]() $Y_{h_j,1}$
is still bounded by
$Y_{h_j,1}$
is still bounded by
![]() $\eta _1 + \frac{\varepsilon }{2}$
. This analytic continuation is possible, since by Lemma 3.11 the pair
$\eta _1 + \frac{\varepsilon }{2}$
. This analytic continuation is possible, since by Lemma 3.11 the pair
![]() $(\rho _{h_j},\eta _{{h_j},1})$
is the only solution to the simultaneous equations
$(\rho _{h_j},\eta _{{h_j},1})$
is the only solution to the simultaneous equations
![]() $F_{h_j}(x,y) = y$
and
$F_{h_j}(x,y) = y$
and
![]() $\frac{\partial }{\partial y} F_{h_j}(x,y) = 1$
with
$\frac{\partial }{\partial y} F_{h_j}(x,y) = 1$
with
![]() $(x,y) \in \Xi _{\varepsilon }^{(1,2)}$
, so the analytic implicit function theorem becomes applicable (compare e.g. the analytic continuation of
$(x,y) \in \Xi _{\varepsilon }^{(1,2)}$
, so the analytic implicit function theorem becomes applicable (compare e.g. the analytic continuation of
![]() $q_h$
in Lemma 3.8). By compactness, this would allow us to extend
$q_h$
in Lemma 3.8). By compactness, this would allow us to extend
![]() $Y_{{h_j},1}$
to
$Y_{{h_j},1}$
to
![]() $D_r(0) \setminus D_{\delta _0}(\rho _{h_j})$
for some
$D_r(0) \setminus D_{\delta _0}(\rho _{h_j})$
for some
![]() $r \gt r_{h_j}$
while still maintaining the inequality
$r \gt r_{h_j}$
while still maintaining the inequality
![]() $|Y_{{h_j},1}(x)| \lt \eta _1 + \frac{\varepsilon }{2}$
, contradicting the choice of
$|Y_{{h_j},1}(x)| \lt \eta _1 + \frac{\varepsilon }{2}$
, contradicting the choice of
![]() $r_{h_j}$
.
$r_{h_j}$
.
Without loss of generality (choosing a subsequence if necessary), we can assume that
![]() $x_{h_j}$
and
$x_{h_j}$
and
![]() $Y_{h_j,1}(x_{h_j})$
have limits
$Y_{h_j,1}(x_{h_j})$
have limits
![]() $x_{\infty }$
and
$x_{\infty }$
and
![]() $y_{\infty }$
, respectively. By construction,
$y_{\infty }$
, respectively. By construction,
![]() $|x_{\infty }| = \rho$
and
$|x_{\infty }| = \rho$
and
![]() $|y_{\infty }| = \eta _1 + \frac{\varepsilon }{2}$
.
$|y_{\infty }| = \eta _1 + \frac{\varepsilon }{2}$
.
Since
![]() $x_{h_j} \notin D_{\delta _0}(\rho )$
for all
$x_{h_j} \notin D_{\delta _0}(\rho )$
for all
![]() $j$
,
$j$
,
![]() $\mathrm{Arg}\, x_{h_j}$
is bounded away from
$\mathrm{Arg}\, x_{h_j}$
is bounded away from
![]() $0$
. Thus we can find
$0$
. Thus we can find
![]() $\alpha \gt 0$
such that
$\alpha \gt 0$
such that
![]() $|\mathrm{Arg}\, x_{h_j}| \geq 2\alpha$
for all
$|\mathrm{Arg}\, x_{h_j}| \geq 2\alpha$
for all
![]() $j$
. Define the region
$j$
. Define the region
![]() $A$
by
$A$
by

Figure 5. Illustration of the domain
![]() $x_{h_j}A$
.
$x_{h_j}A$
.
Note that
![]() $x_{h_j}A$
avoids the part of the real axis that includes
$x_{h_j}A$
avoids the part of the real axis that includes
![]() $\rho _{h_j}$
(see Fig. 5), so the function
$\rho _{h_j}$
(see Fig. 5), so the function
![]() $Y_{h_j,1}(x)$
is analytic in this region for all
$Y_{h_j,1}(x)$
is analytic in this region for all
![]() $j$
by construction since
$j$
by construction since
![]() $(x, Y_{h_j,1}(x))\in \Xi _\varepsilon ^{(1,2)}$
whenever
$(x, Y_{h_j,1}(x))\in \Xi _\varepsilon ^{(1,2)}$
whenever
![]() $x \in x_{h_j}A$
. So we have a sequence of functions
$x \in x_{h_j}A$
. So we have a sequence of functions
![]() $W_j(z) \,{:\!=}\, Y_{h_j,1}(x_{h_j}z)$
that are all analytic on
$W_j(z) \,{:\!=}\, Y_{h_j,1}(x_{h_j}z)$
that are all analytic on
![]() $A$
and are uniformly bounded above by
$A$
and are uniformly bounded above by
![]() $\eta _1 + \frac{\varepsilon }{2}$
by our choice of
$\eta _1 + \frac{\varepsilon }{2}$
by our choice of
![]() $x_{h_j}$
. By Montel’s theorem, there is a subsequence of these functions (without loss of generality the sequence itself) that converges locally uniformly and thus to an analytic function
$x_{h_j}$
. By Montel’s theorem, there is a subsequence of these functions (without loss of generality the sequence itself) that converges locally uniformly and thus to an analytic function
![]() $W_\infty$
on
$W_\infty$
on
![]() $A$
. This function needs to satisfy the following:
$A$
. This function needs to satisfy the following:
-
•
 $W_{\infty }(0) = 0$
, since
$W_{\infty }(0) = 0$
, since
 $W_j(0) = 0$
for all
$W_j(0) = 0$
for all
 $j$
,
$j$
, -
•
 $W_{\infty }(z) = F_{\infty }(x_{\infty }z, W_{\infty }(z)) = x_{\infty }z(\Phi (x_{\infty }z + W_{\infty }(z))-1)$
for
$W_{\infty }(z) = F_{\infty }(x_{\infty }z, W_{\infty }(z)) = x_{\infty }z(\Phi (x_{\infty }z + W_{\infty }(z))-1)$
for
 $z\in A$
, since we have the uniform estimateThis is also equivalent to
$z\in A$
, since we have the uniform estimateThis is also equivalent to \begin{equation*}W_j(z)=Y_{h_j,1}(x_{h_j}z)=F_{h_j}(x_{h_j}z, Y_{h_j,1}(x_{h_j}z))=F_{\infty }(x_{h_j}z, Y_{h_j,1}(x_{h_j}z)) + O(\lambda ^h).\end{equation*}
\begin{equation*}W_j(z)=Y_{h_j,1}(x_{h_j}z)=F_{h_j}(x_{h_j}z, Y_{h_j,1}(x_{h_j}z))=F_{\infty }(x_{h_j}z, Y_{h_j,1}(x_{h_j}z)) + O(\lambda ^h).\end{equation*}
 \begin{equation*} x_{\infty }z + W_{\infty }(z) = x_{\infty }z\Phi (x_{\infty }z + W_{\infty }(z)). \end{equation*}
\begin{equation*} x_{\infty }z + W_{\infty }(z) = x_{\infty }z\Phi (x_{\infty }z + W_{\infty }(z)). \end{equation*}
These two properties imply that
![]() $W_{\infty }(z) =Y(x_{\infty }z) - x_{\infty }z$
, since
$W_{\infty }(z) =Y(x_{\infty }z) - x_{\infty }z$
, since
![]() $Y$
is the unique function that is analytic at
$Y$
is the unique function that is analytic at
![]() $0$
and satisfies the implicit equation
$0$
and satisfies the implicit equation
![]() $Y(x) = x \Phi (Y(x))$
. Implicit differentiation of
$Y(x) = x \Phi (Y(x))$
. Implicit differentiation of
![]() $Y_{h_j,1}(x)=F_{h_j}(x, Y_{h_j, 1}(x))$
for
$Y_{h_j,1}(x)=F_{h_j}(x, Y_{h_j, 1}(x))$
for
![]() $x \in x_{h_j}A$
yields
$x \in x_{h_j}A$
yields
 \begin{equation} Y_{h_j,1}^{\prime}(x) = \frac{\frac{\partial F_{h_j}}{\partial x} (x, Y_{h_j, 1}(x))}{1 - \frac{\partial F_{h_j}}{\partial y} (x, Y_{h_j, 1}(x))} = \frac{\frac{\partial F_{\infty }}{\partial x} (x, Y_{h_j, 1}(x)) + O(\lambda ^{h_j})}{1 - \frac{\partial F_{\infty }}{\partial y} (x, Y_{h_j, 1}(x)) + O(\lambda ^{h_j})}. \end{equation}
\begin{equation} Y_{h_j,1}^{\prime}(x) = \frac{\frac{\partial F_{h_j}}{\partial x} (x, Y_{h_j, 1}(x))}{1 - \frac{\partial F_{h_j}}{\partial y} (x, Y_{h_j, 1}(x))} = \frac{\frac{\partial F_{\infty }}{\partial x} (x, Y_{h_j, 1}(x)) + O(\lambda ^{h_j})}{1 - \frac{\partial F_{\infty }}{\partial y} (x, Y_{h_j, 1}(x)) + O(\lambda ^{h_j})}. \end{equation}
Note that the numerator is uniformly bounded. Moreover, we recall again that the only solution to the simultaneous equations
![]() $F_{\infty }(x,y) = x(\Phi (y+x) - 1) = y$
and
$F_{\infty }(x,y) = x(\Phi (y+x) - 1) = y$
and
![]() $\frac{\partial }{\partial y}F_{\infty }(x,y) = x \Phi '(y+x) = 1$
with
$\frac{\partial }{\partial y}F_{\infty }(x,y) = x \Phi '(y+x) = 1$
with
![]() $|{x}| \leq \rho + \varepsilon$
and
$|{x}| \leq \rho + \varepsilon$
and
![]() $|x+y| \leq \tau + \varepsilon$
is
$|x+y| \leq \tau + \varepsilon$
is
![]() $(x,y) = (\rho,\tau -\rho ) = (\rho,\eta _1)$
by our assumptions on
$(x,y) = (\rho,\tau -\rho ) = (\rho,\eta _1)$
by our assumptions on
![]() $\Phi$
. By construction, there is a constant
$\Phi$
. By construction, there is a constant
![]() $\varepsilon _A \gt 0$
such that
$\varepsilon _A \gt 0$
such that
![]() $|x - \rho | \geq \varepsilon _A$
whenever
$|x - \rho | \geq \varepsilon _A$
whenever
![]() $x \in x_{h_j}A$
for some
$x \in x_{h_j}A$
for some
![]() $j$
. The map
$j$
. The map
![]() $(x, y)\mapsto \| (F_{\infty }(x,y) - y, \frac{\partial }{\partial y}F_{\infty }(x,y) - 1)\|$
is continuous on the compact set
$(x, y)\mapsto \| (F_{\infty }(x,y) - y, \frac{\partial }{\partial y}F_{\infty }(x,y) - 1)\|$
is continuous on the compact set
and has no zero there (using the Euclidean norm on
![]() ${\mathbb{C}}^2$
). Therefore, it attains a minimum
${\mathbb{C}}^2$
). Therefore, it attains a minimum
![]() $\delta _A\gt 0$
on
$\delta _A\gt 0$
on
![]() $\mathcal{K}$
.
$\mathcal{K}$
.
Now for
![]() $x \in x_{h_j}A$
,
$x \in x_{h_j}A$
,
![]() $|{x}| \leq \rho + \varepsilon$
holds by assumption, as does
$|{x}| \leq \rho + \varepsilon$
holds by assumption, as does
![]() $|x + Y_{h_j, 1}(x)| \leq \tau + \varepsilon$
. Moreover,
$|x + Y_{h_j, 1}(x)| \leq \tau + \varepsilon$
. Moreover,
![]() $|x - \rho | \geq \varepsilon _A$
. Thus we can conclude that
$|x - \rho | \geq \varepsilon _A$
. Thus we can conclude that
![]() $(x, Y_{h_j,1}(x)) \in \mathcal{K}$
and therefore
$(x, Y_{h_j,1}(x)) \in \mathcal{K}$
and therefore
![]() $\| (F_{\infty }(x,Y_{h_j, 1}(x)) - Y_{h_j, 1}(x), \frac{\partial F_{\infty }}{\partial y}(x,Y_{h_j, 1}(x)) - 1)\| \geq \delta _A$
for all such
$\| (F_{\infty }(x,Y_{h_j, 1}(x)) - Y_{h_j, 1}(x), \frac{\partial F_{\infty }}{\partial y}(x,Y_{h_j, 1}(x)) - 1)\| \geq \delta _A$
for all such
![]() $x$
. Since
$x$
. Since
this means that
![]() $\left |{1 - \frac{\partial F_{\infty }}{\partial y} (x, Y_{h_j, 1}(x))}\right | \geq \delta _A - O(\lambda ^{h_j})$
, so that the denominator in (43) is bounded below by a positive constant for sufficiently large
$\left |{1 - \frac{\partial F_{\infty }}{\partial y} (x, Y_{h_j, 1}(x))}\right | \geq \delta _A - O(\lambda ^{h_j})$
, so that the denominator in (43) is bounded below by a positive constant for sufficiently large
![]() $j$
.
$j$
.
So we can conclude that
![]() $Y_{h_j,1}^{\prime}(x)$
is uniformly bounded by a constant for
$Y_{h_j,1}^{\prime}(x)$
is uniformly bounded by a constant for
![]() $x \in x_{h_j}A$
, implying that
$x \in x_{h_j}A$
, implying that
![]() $W_j'(z)$
is uniformly bounded (for all
$W_j'(z)$
is uniformly bounded (for all
![]() $z \in A$
and all sufficiently large
$z \in A$
and all sufficiently large
![]() $j$
) by a constant that is independent of
$j$
) by a constant that is independent of
![]() $j$
. Therefore,
$j$
. Therefore,
![]() $W_j(z)$
is a uniformly equicontinuous sequence of functions on
$W_j(z)$
is a uniformly equicontinuous sequence of functions on
![]() $\overline{A}$
, the closure of
$\overline{A}$
, the closure of
![]() $A$
. By the Arzelà–Ascoli theorem, this implies that
$A$
. By the Arzelà–Ascoli theorem, this implies that
![]() $W_j(z) \to W_{\infty }(z) = Y(x_{\infty }z) - x_{\infty }z$
holds even for all
$W_j(z) \to W_{\infty }(z) = Y(x_{\infty }z) - x_{\infty }z$
holds even for all
![]() $z \in \overline{A}$
, not only on
$z \in \overline{A}$
, not only on
![]() $A$
. In particular,
$A$
. In particular,
![]() $y_{\infty } = W_{\infty }(1) = Y(x_{\infty }) - x_{\infty }$
. Here, we have
$y_{\infty } = W_{\infty }(1) = Y(x_{\infty }) - x_{\infty }$
. Here, we have
![]() $|{x_{\infty }}| \leq \rho$
and
$|{x_{\infty }}| \leq \rho$
and
![]() $|{y_{\infty }}| = \eta _1 + \frac{\varepsilon }{2}$
by assumption. However,
$|{y_{\infty }}| = \eta _1 + \frac{\varepsilon }{2}$
by assumption. However,
holds for all
![]() $|{x}| \leq \rho$
by the triangle inequality, so we finally reach a contradiction.
$|{x}| \leq \rho$
by the triangle inequality, so we finally reach a contradiction.
We conclude this section with a summary of the results proven so far. The following proposition follows by combining the last two lemmata.
Proposition 3.16.
There exists a constant
![]() $\delta \gt 0$
such that
$\delta \gt 0$
such that
![]() $Y_{h,1}(x)$
can be continued analytically to the domain
$Y_{h,1}(x)$
can be continued analytically to the domain
for every sufficiently large
![]() $h$
. Moreover,
$h$
. Moreover,
![]() $Y_{h,1}(x)$
is then uniformly bounded on this domain by a constant that is independent of
$Y_{h,1}(x)$
is then uniformly bounded on this domain by a constant that is independent of
![]() $h$
, and the following singular expansion holds near the singularity:
$h$
, and the following singular expansion holds near the singularity:
where the
![]() $O$
-constant is independent of
$O$
-constant is independent of
![]() $h$
and
$h$
and
![]() $a_h,b_h,c_h$
converge at an exponential rate to
$a_h,b_h,c_h$
converge at an exponential rate to
![]() $a,b,c$
respectively as
$a,b,c$
respectively as
![]() $h \to \infty$
.
$h \to \infty$
.
Remark 3.17.
Let
![]() $D=\gcd \{i\in \mathbb{N}\colon w_i\neq 0\}$
be the period of
$D=\gcd \{i\in \mathbb{N}\colon w_i\neq 0\}$
be the period of
![]() $\Phi$
. The purpose of this remark is to give indications how the results so far have to be adapted for the case
$\Phi$
. The purpose of this remark is to give indications how the results so far have to be adapted for the case
![]() $D\gt 1$
.
$D\gt 1$
.
If
![]() $D\gt 1$
, then for all trees of our simply generated family of trees, the number
$D\gt 1$
, then for all trees of our simply generated family of trees, the number
![]() $n$
of vertices will be congruent to
$n$
of vertices will be congruent to
![]() $1$
modulo
$1$
modulo
![]() $D$
because all outdegrees are multiples of
$D$
because all outdegrees are multiples of
![]() $D$
. Trivially, the same is true for all trees with maximum protection number
$D$
. Trivially, the same is true for all trees with maximum protection number
![]() $h$
.
$h$
.
By [10, Remark VI.17], both
![]() $Y$
and
$Y$
and
![]() $Y_{h,1}$
have
$Y_{h,1}$
have
![]() $D$
conjugate roots on its circle of convergence. Therefore, it is enough to study the positive root at the radius of convergence. Up to Theorem
3.10
, no changes are required. In Lemma 3.11
, there are exactly
$D$
conjugate roots on its circle of convergence. Therefore, it is enough to study the positive root at the radius of convergence. Up to Theorem
3.10
, no changes are required. In Lemma 3.11
, there are exactly
![]() $D$
solutions instead of exactly one solution to the simultaneous equations. Lemmata 3.12, 3.13, and 3.14 analyse the behaviour of
$D$
solutions instead of exactly one solution to the simultaneous equations. Lemmata 3.12, 3.13, and 3.14 analyse the behaviour of
![]() $Y_{h,1}$
around the dominant positive singularity and remain valid without any change. In the proof of Lemma 3.15
, we need to exclude balls around the conjugate roots. Proposition 3.16 must also be changed to exclude the conjugate roots.
$Y_{h,1}$
around the dominant positive singularity and remain valid without any change. In the proof of Lemma 3.15
, we need to exclude balls around the conjugate roots. Proposition 3.16 must also be changed to exclude the conjugate roots.
4. The exponential case:
 $w_1 \neq 0$
$w_1 \neq 0$
4.1 Asymptotics of the singularities
Proposition 3.16 that concluded the previous section shows that condition (2) of Theorem 2.1 is satisfied (with
![]() $\alpha = \frac 12$
) by the generating functions
$\alpha = \frac 12$
) by the generating functions
![]() $Y_{h,1}$
(and thus also
$Y_{h,1}$
(and thus also
![]() $Y_{h,0}$
, since
$Y_{h,0}$
, since
![]() $Y_{h,0}(x) = Y_{h,1}(x) + x$
). It remains to study the behaviour of the singularity
$Y_{h,0}(x) = Y_{h,1}(x) + x$
). It remains to study the behaviour of the singularity
![]() $\rho _h$
of
$\rho _h$
of
![]() $Y_{h,0}$
and
$Y_{h,0}$
and
![]() $Y_{h,1}$
to make the theorem applicable. As it turns out, condition (1) of Theorem 2.1 holds precisely if vertices of outdegree
$Y_{h,1}$
to make the theorem applicable. As it turns out, condition (1) of Theorem 2.1 holds precisely if vertices of outdegree
![]() $1$
are allowed in our simply generated family of trees. In terms of the weight generating function
$1$
are allowed in our simply generated family of trees. In terms of the weight generating function
![]() $\Phi$
, this can be expressed as
$\Phi$
, this can be expressed as
![]() $w_1 = \Phi '(0) \neq 0$
. Starting with Lemma 4.3, we will assume that this holds. The case where vertices of outdegree
$w_1 = \Phi '(0) \neq 0$
. Starting with Lemma 4.3, we will assume that this holds. The case where vertices of outdegree
![]() $1$
cannot occur (equivalently,
$1$
cannot occur (equivalently,
![]() $w_1 = \Phi '(0) = 0$
) is covered in Section 5.
$w_1 = \Phi '(0) = 0$
) is covered in Section 5.
Let us define the auxiliary quantities
![]() $\eta _{h,k} \,{:\!=}\, Y_{h,k}(\rho _h)$
for all
$\eta _{h,k} \,{:\!=}\, Y_{h,k}(\rho _h)$
for all
![]() $0 \leq k \leq h$
. We know that these must exist and be finite for all sufficiently large
$0 \leq k \leq h$
. We know that these must exist and be finite for all sufficiently large
![]() $h$
. Since the coefficients of
$h$
. Since the coefficients of
![]() $Y_{h,k}$
are nonincreasing in
$Y_{h,k}$
are nonincreasing in
![]() $k$
in view of the combinatorial interpretation, we must have
$k$
in view of the combinatorial interpretation, we must have
Note also that the following system of equations holds:
in view of (8) and (7), respectively. Since
![]() $Y_{h,1}$
is singular at
$Y_{h,1}$
is singular at
![]() $\rho _h$
by assumption, the Jacobian determinant of the system that determines
$\rho _h$
by assumption, the Jacobian determinant of the system that determines
![]() $Y_{h,0},Y_{h,1},\ldots,Y_{h,h}$
needs to vanish (as there would otherwise be an analytic continuation by the analytic implicit function theorem). This determinant is given by
$Y_{h,0},Y_{h,1},\ldots,Y_{h,h}$
needs to vanish (as there would otherwise be an analytic continuation by the analytic implicit function theorem). This determinant is given by
 \begin{equation*} \begin {vmatrix} 1 & -1 & 0 & \cdots & 0 & 0 \\ -\rho _h \Phi '(\eta _{h,0}) & 1 & 0 & \cdots & 0 & \rho _h \Phi '(\eta _{h,h}) \\ 0 & -\rho _h \Phi '(\eta _{h,1}) & 1 & \cdots & 0 & \rho _h \Phi '(\eta _{h,h}) \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & -\rho _h \Phi '(\eta _{h,h-1}) & 1 + \rho _h \Phi '(\eta _{h,h}) \end {vmatrix}\,. \end{equation*}
\begin{equation*} \begin {vmatrix} 1 & -1 & 0 & \cdots & 0 & 0 \\ -\rho _h \Phi '(\eta _{h,0}) & 1 & 0 & \cdots & 0 & \rho _h \Phi '(\eta _{h,h}) \\ 0 & -\rho _h \Phi '(\eta _{h,1}) & 1 & \cdots & 0 & \rho _h \Phi '(\eta _{h,h}) \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & \cdots & -\rho _h \Phi '(\eta _{h,h-1}) & 1 + \rho _h \Phi '(\eta _{h,h}) \end {vmatrix}\,. \end{equation*}
Using column expansion with respect to the last column to obtain the determinant, we find that this simplifies to
 \begin{equation} \prod _{j=1}^{h} \big ( \rho _h \Phi '(\eta _{h,j}) \big ) + \big (1 - \rho _h \Phi '(\eta _{h,0}) \big ) \Big ( 1 + \sum _{k=2}^{h} \prod _{j=k}^{h} \big ( \rho _h \Phi '(\eta _{h,j}) \big ) \Big ) = 0. \end{equation}
\begin{equation} \prod _{j=1}^{h} \big ( \rho _h \Phi '(\eta _{h,j}) \big ) + \big (1 - \rho _h \Phi '(\eta _{h,0}) \big ) \Big ( 1 + \sum _{k=2}^{h} \prod _{j=k}^{h} \big ( \rho _h \Phi '(\eta _{h,j}) \big ) \Big ) = 0. \end{equation}
We will now use (45), (46), and (47) to determine an asymptotic formula for
![]() $\rho _h$
. Throughout this section,
$\rho _h$
. Throughout this section,
![]() $B_i$
’s will always be positive constants with
$B_i$
’s will always be positive constants with
![]() $B_i \lt 1$
that depend on the specific family of simply generated trees, but nothing else.
$B_i \lt 1$
that depend on the specific family of simply generated trees, but nothing else.
Lemma 4.1.
There exist positive constants
![]() $C$
and
$C$
and
![]() $B_1$
with
$B_1$
with
![]() $B_1 \lt 1$
such that
$B_1 \lt 1$
such that
![]() $\eta _{h,k} \leq C B_1^k$
for all sufficiently large
$\eta _{h,k} \leq C B_1^k$
for all sufficiently large
![]() $h$
and all
$h$
and all
![]() $k$
with
$k$
with
![]() $0 \leq k \leq h$
.
$0 \leq k \leq h$
.
Proof. Since we already know that
![]() $\eta _{h,1}$
converges to
$\eta _{h,1}$
converges to
![]() $\tau - \rho$
and that
$\tau - \rho$
and that
![]() $\rho _h$
converges to
$\rho _h$
converges to
![]() $\rho$
,
$\rho$
,
![]() $\eta _{h,0}$
converges to
$\eta _{h,0}$
converges to
![]() $\tau$
by (45). By the monotonicity property (44), all
$\tau$
by (45). By the monotonicity property (44), all
![]() $\eta _{h,k}$
must therefore be bounded by a single constant
$\eta _{h,k}$
must therefore be bounded by a single constant
![]() $M$
for sufficiently large
$M$
for sufficiently large
![]() $h$
. Since
$h$
. Since
![]() $\eta _{h,1}$
converges to
$\eta _{h,1}$
converges to
![]() $\tau - \rho$
, we must have that
$\tau - \rho$
, we must have that
![]() $\rho _h\Phi '(\eta _{h, 1})$
converges to
$\rho _h\Phi '(\eta _{h, 1})$
converges to
![]() $\rho \Phi '(\tau -\rho )$
. Therefore,
$\rho \Phi '(\tau -\rho )$
. Therefore,
![]() $\rho _h\Phi '(\eta _{h, 1}) \le \rho \Phi '(\tau - \rho/2)$
for sufficiently large
$\rho _h\Phi '(\eta _{h, 1}) \le \rho \Phi '(\tau - \rho/2)$
for sufficiently large
![]() $h$
. It follows that
$h$
. It follows that
![]() $\rho _h \Phi '(\eta _{h,1}) \leq \rho \Phi '(\tau - \rho/2) \lt \rho \Phi '(\tau ) = 1$
. For all
$\rho _h \Phi '(\eta _{h,1}) \leq \rho \Phi '(\tau - \rho/2) \lt \rho \Phi '(\tau ) = 1$
. For all
![]() $1 \leq j \leq h$
, we now have
$1 \leq j \leq h$
, we now have
Thus by induction
This proves the desired inequality for sufficiently large
![]() $h$
and
$h$
and
![]() $1 \leq k \leq h$
with
$1 \leq k \leq h$
with
![]() $B_1 = \rho \Phi '(\tau - \rho/2)\,{\lt}\,1$
, and we are done.
$B_1 = \rho \Phi '(\tau - \rho/2)\,{\lt}\,1$
, and we are done.
With this bound, we will be able to refine the estimates for the system of equations, leading to better estimates for
![]() $\rho _h$
and
$\rho _h$
and
![]() $\eta _{h, 0}$
. Recall from Lemma 3.9 that
$\eta _{h, 0}$
. Recall from Lemma 3.9 that
![]() $\rho _h$
and
$\rho _h$
and
![]() $\eta _{h,1}$
converge to their respective limits
$\eta _{h,1}$
converge to their respective limits
![]() $\rho$
and
$\rho$
and
![]() $\tau - \rho = \eta _1$
(at least) exponentially fast. Since
$\tau - \rho = \eta _1$
(at least) exponentially fast. Since
![]() $\eta _{h,0} = \eta _{h,1} + \rho _h$
by (45), this also applies to
$\eta _{h,0} = \eta _{h,1} + \rho _h$
by (45), this also applies to
![]() $\eta _{h,0}$
. We show that an analogous statement also holds for
$\eta _{h,0}$
. We show that an analogous statement also holds for
![]() $\eta _{h,k}$
with arbitrary
$\eta _{h,k}$
with arbitrary
![]() $k$
. In view of (46), it is natural to expect that
$k$
. In view of (46), it is natural to expect that
![]() $\eta _{h,k} \to \eta _k$
, where
$\eta _{h,k} \to \eta _k$
, where
![]() $\eta _k$
is defined recursively as follows:
$\eta _k$
is defined recursively as follows:
![]() $\eta _0 = \tau$
and, for
$\eta _0 = \tau$
and, for
![]() $k \gt 0$
,
$k \gt 0$
,
![]() $\eta _k = \rho \Phi (\eta _{k-1}) - \rho$
, which also coincides with our earlier definition of
$\eta _k = \rho \Phi (\eta _{k-1}) - \rho$
, which also coincides with our earlier definition of
![]() $\eta _1 = \tau - \rho$
. This is proven in the following lemma.
$\eta _1 = \tau - \rho$
. This is proven in the following lemma.
Lemma 4.2.
For a suitable constant
![]() $B_2 \lt 1$
and sufficiently large
$B_2 \lt 1$
and sufficiently large
![]() $h$
, we have
$h$
, we have
![]() $\rho _h = \rho + O(B_2^h)$
and
$\rho _h = \rho + O(B_2^h)$
and
![]() $\eta _{h,k} = \eta _k + O(B_2^h)$
for all
$\eta _{h,k} = \eta _k + O(B_2^h)$
for all
![]() $k$
with
$k$
with
![]() $0 \leq k \leq h$
, uniformly in
$0 \leq k \leq h$
, uniformly in
![]() $k$
.
$k$
.
Proof. For a suitable choice of
![]() $B_2$
, the estimate for
$B_2$
, the estimate for
![]() $\rho _h$
has been established by Lemma 3.9, as has the estimate for
$\rho _h$
has been established by Lemma 3.9, as has the estimate for
![]() $\eta _{h,k}$
in the cases where
$\eta _{h,k}$
in the cases where
![]() $k = 0$
and
$k = 0$
and
![]() $k = 1$
. Set
$k = 1$
. Set
![]() $\delta _{h, k} = \eta _{h, k} - \eta _k$
. Since
$\delta _{h, k} = \eta _{h, k} - \eta _k$
. Since
![]() $\eta _{h,h} \leq C B_1^h$
by Lemma 4.1, we have
$\eta _{h,h} \leq C B_1^h$
by Lemma 4.1, we have
![]() $\Phi (\eta _{h,h}) = \Phi (0) + O(B_1^h) = 1 + O(B_1^h)$
. Without loss of generality, suppose that
$\Phi (\eta _{h,h}) = \Phi (0) + O(B_1^h) = 1 + O(B_1^h)$
. Without loss of generality, suppose that
![]() $B_2 \geq B_1$
. Then, using (46), we obtain
$B_2 \geq B_1$
. Then, using (46), we obtain
 \begin{align*} \eta _{h, k} & = \rho _h\Phi (\eta _{h, k-1}) - \rho _h\Phi (\eta _{h, h}) \\ & = (\rho + O(B_2^h))\Phi (\eta _{k-1}+ \delta _{h, k-1}) - (\rho + O(B_2^h))(1 + O(B_1^h))\\ & = \rho (\Phi (\eta _{k-1}) + \Phi '(\xi _{h, k-1})\delta _{h, k-1}) - \rho + O(B_2^h) \\ & = \eta _k + \rho \Phi '(\xi _{h,k-1}) \delta _{h,k-1} + O(B_2^h) \end{align*}
\begin{align*} \eta _{h, k} & = \rho _h\Phi (\eta _{h, k-1}) - \rho _h\Phi (\eta _{h, h}) \\ & = (\rho + O(B_2^h))\Phi (\eta _{k-1}+ \delta _{h, k-1}) - (\rho + O(B_2^h))(1 + O(B_1^h))\\ & = \rho (\Phi (\eta _{k-1}) + \Phi '(\xi _{h, k-1})\delta _{h, k-1}) - \rho + O(B_2^h) \\ & = \eta _k + \rho \Phi '(\xi _{h,k-1}) \delta _{h,k-1} + O(B_2^h) \end{align*}
where
![]() $\xi _{h, k-1}$
is between
$\xi _{h, k-1}$
is between
![]() $\eta _{k-1}$
and
$\eta _{k-1}$
and
![]() $\eta _{h, k-1}$
(by the mean value theorem) and the
$\eta _{h, k-1}$
(by the mean value theorem) and the
![]() $O$
-constant is independent of
$O$
-constant is independent of
![]() $k$
. Let
$k$
. Let
![]() $M$
be this
$M$
be this
![]() $O$
-constant. We already know (compare the proof of Lemma 4.1) that
$O$
-constant. We already know (compare the proof of Lemma 4.1) that
![]() $\eta _{h,k-1} \leq \eta _{h,1} \leq \tau - \rho/2$
for every
$\eta _{h,k-1} \leq \eta _{h,1} \leq \tau - \rho/2$
for every
![]() $k \geq 2$
if
$k \geq 2$
if
![]() $h$
is sufficiently large. Likewise, it is easy to see that
$h$
is sufficiently large. Likewise, it is easy to see that
![]() $\eta _k$
is decreasing in
$\eta _k$
is decreasing in
![]() $k$
, hence
$k$
, hence
![]() $\eta _{k-1} \leq \eta _1 = \tau - \rho$
. Thus,
$\eta _{k-1} \leq \eta _1 = \tau - \rho$
. Thus,
![]() $\xi _{h,k-1} \leq \tau - \rho/2$
and
$\xi _{h,k-1} \leq \tau - \rho/2$
and
![]() $\rho \Phi '(\xi _{h, k-1}) \leq \rho \Phi '(\tau - \rho/2) = B_1 \lt 1$
. So we have, for every
$\rho \Phi '(\xi _{h, k-1}) \leq \rho \Phi '(\tau - \rho/2) = B_1 \lt 1$
. So we have, for every
![]() $k \gt 1$
,
$k \gt 1$
,
Iterating this inequality yields
and the desired statement follows.
From Lemma 4.1 and the fact that
![]() $\eta _{h,k} \to \eta _k$
, we trivially obtain
$\eta _{h,k} \to \eta _k$
, we trivially obtain
![]() $\eta _k \leq C \cdot B_1^k$
, with the same constants
$\eta _k \leq C \cdot B_1^k$
, with the same constants
![]() $B_1$
and
$B_1$
and
![]() $C$
as in Lemma 4.1. In fact, we can be more precise, and this is demonstrated in the lemma that follows. Since the expression
$C$
as in Lemma 4.1. In fact, we can be more precise, and this is demonstrated in the lemma that follows. Since the expression
![]() $\rho \Phi '(0)$
occurs frequently in the following, we set
$\rho \Phi '(0)$
occurs frequently in the following, we set
![]() $\zeta \,{:\!=}\, \rho \Phi '(0)$
. Recall that we assume
$\zeta \,{:\!=}\, \rho \Phi '(0)$
. Recall that we assume
![]() $\Phi '(0) \neq 0$
until the end of this section.
$\Phi '(0) \neq 0$
until the end of this section.
Lemma 4.3.
The limit
![]() $\lambda _1 \,{:\!=}\, \lim _{k \to \infty } \zeta ^{-k} \eta _k$
exists. Moreover, we have
$\lambda _1 \,{:\!=}\, \lim _{k \to \infty } \zeta ^{-k} \eta _k$
exists. Moreover, we have
with
![]() $B_1$
as in Lemma 4.1
.
$B_1$
as in Lemma 4.1
.
Proof. Recall that we defined the sequence
![]() $(\eta _k)_{k \geq 0}$
by
$(\eta _k)_{k \geq 0}$
by
![]() $\eta _0 = \tau$
and
$\eta _0 = \tau$
and
![]() $\eta _k = \rho \Phi (\eta _{k-1}) - \rho$
for
$\eta _k = \rho \Phi (\eta _{k-1}) - \rho$
for
![]() $k\ge 1$
. Using Taylor expansion, we obtain
$k\ge 1$
. Using Taylor expansion, we obtain
Since we already know that
![]() $\eta _{k-1} \leq C \cdot B_1^{k-1}$
, this implies that
$\eta _{k-1} \leq C \cdot B_1^{k-1}$
, this implies that
Now it follows that the infinite product
 \begin{equation*} \lambda _1 = \eta _0 \prod _{j \geq 1} \frac {\eta _j}{\zeta \eta _{j-1}} = \lim _{k \to \infty } \eta _0 \prod _{j = 1}^k \frac {\eta _j}{\zeta \eta _{j-1}} = \lim _{k \to \infty } \zeta ^{-k} \eta _k \end{equation*}
\begin{equation*} \lambda _1 = \eta _0 \prod _{j \geq 1} \frac {\eta _j}{\zeta \eta _{j-1}} = \lim _{k \to \infty } \eta _0 \prod _{j = 1}^k \frac {\eta _j}{\zeta \eta _{j-1}} = \lim _{k \to \infty } \zeta ^{-k} \eta _k \end{equation*}
converges. The error bound follows from noting that
Next, we consider the expression in (47) and determine the asymptotic behaviour of its parts.
Lemma 4.4.
For large enough
![]() $h$
and a fixed constant
$h$
and a fixed constant
![]() $B_3 \lt 1$
, we have
$B_3 \lt 1$
, we have
 \begin{equation*} 1 + \sum _{k = 2}^{h}\prod _{j = k}^{h} (\rho _h \Phi '(\eta _{h, j})) = \frac {1}{1 - \zeta } + O(B_3^{h}) \end{equation*}
\begin{equation*} 1 + \sum _{k = 2}^{h}\prod _{j = k}^{h} (\rho _h \Phi '(\eta _{h, j})) = \frac {1}{1 - \zeta } + O(B_3^{h}) \end{equation*}
and
 \begin{equation*} \prod _{j=1}^{h}\rho _h\Phi '(\eta _{h, j}) = \lambda _2 \zeta ^h (1 + O(B_3^h)), \end{equation*}
\begin{equation*} \prod _{j=1}^{h}\rho _h\Phi '(\eta _{h, j}) = \lambda _2 \zeta ^h (1 + O(B_3^h)), \end{equation*}
where
![]() $\lambda _2 \,{:\!=}\, \prod _{j\geq 1}\frac{\Phi '(\eta _j)}{\Phi '(0)}$
.
$\lambda _2 \,{:\!=}\, \prod _{j\geq 1}\frac{\Phi '(\eta _j)}{\Phi '(0)}$
.
Proof. Note that
 \begin{equation*} \prod _{j = k}^{h} (\rho _h \Phi '(\eta _{h, j})) = \rho _h^{h-k+1} \prod _{j = k}^{h} \Phi '(\eta _{h,j}). \end{equation*}
\begin{equation*} \prod _{j = k}^{h} (\rho _h \Phi '(\eta _{h, j})) = \rho _h^{h-k+1} \prod _{j = k}^{h} \Phi '(\eta _{h,j}). \end{equation*}
In view of Lemma 4.2, we have
![]() $\rho _h^{h-k+1} = \rho ^{h-k+1} (1+O(B_2^h))^{h-k+1} = \rho ^{h-k+1}(1+ O(hB_2^h))$
, uniformly in
$\rho _h^{h-k+1} = \rho ^{h-k+1} (1+O(B_2^h))^{h-k+1} = \rho ^{h-k+1}(1+ O(hB_2^h))$
, uniformly in
![]() $k$
. Moreover, Lemma 4.1 yields
$k$
. Moreover, Lemma 4.1 yields
![]() $\Phi '(\eta _{h,j}) = \Phi '(0) + O(\eta _{h,j}) = \Phi '(0) + O(B_1^j)$
, uniformly in
$\Phi '(\eta _{h,j}) = \Phi '(0) + O(\eta _{h,j}) = \Phi '(0) + O(B_1^j)$
, uniformly in
![]() $h$
. Thus
$h$
. Thus
 \begin{equation*} \prod _{j = k}^{h} \Phi '(\eta _{h,j}) = \Phi '(0)^{h-k+1} \prod _{j=k}^h (1 + O(B_1^j)) = \Phi '(0)^{h-k+1} (1 + O(B_1^k)). \end{equation*}
\begin{equation*} \prod _{j = k}^{h} \Phi '(\eta _{h,j}) = \Phi '(0)^{h-k+1} \prod _{j=k}^h (1 + O(B_1^j)) = \Phi '(0)^{h-k+1} (1 + O(B_1^k)). \end{equation*}
Hence the expression simplifies to
 \begin{equation*} 1 + \sum _{k = 2}^{h}\prod _{j = k}^{h} (\rho _h \Phi '(\eta _{h, j})) = 1 + (1 + O(hB_2^h)) \sum _{k = 2}^h \zeta ^{h-k+1}(1 + O(B_1^k)). \end{equation*}
\begin{equation*} 1 + \sum _{k = 2}^{h}\prod _{j = k}^{h} (\rho _h \Phi '(\eta _{h, j})) = 1 + (1 + O(hB_2^h)) \sum _{k = 2}^h \zeta ^{h-k+1}(1 + O(B_1^k)). \end{equation*}
Since
![]() $\zeta \lt 1$
and
$\zeta \lt 1$
and
![]() $B_1 \lt 1$
, we can simply evaluate the geometric series, and the expression further simplifies to
$B_1 \lt 1$
, we can simply evaluate the geometric series, and the expression further simplifies to
 \begin{equation*} 1 + \sum _{k = 2}^h \zeta ^{h-k+1} + O(B_3^h) = \frac {1-\zeta ^h}{1-\zeta } + O(B_3^h) = \frac {1}{1-\zeta } + O(B_3^h) \end{equation*}
\begin{equation*} 1 + \sum _{k = 2}^h \zeta ^{h-k+1} + O(B_3^h) = \frac {1-\zeta ^h}{1-\zeta } + O(B_3^h) = \frac {1}{1-\zeta } + O(B_3^h) \end{equation*}
for an appropriately chosen
![]() $B_3 \lt 1$
. This proves the first statement. For the second statement, we also use Lemma 4.2, along with the monotonicity of
$B_3 \lt 1$
. This proves the first statement. For the second statement, we also use Lemma 4.2, along with the monotonicity of
![]() $\Phi '$
and the assumption that
$\Phi '$
and the assumption that
![]() $\Phi '(0) \neq 0$
, which implies that
$\Phi '(0) \neq 0$
, which implies that
![]() $\Phi '(\eta _j)$
is bounded away from
$\Phi '(\eta _j)$
is bounded away from
![]() $0$
. This yields
$0$
. This yields
 \begin{align*} \prod _{j=1}^{h}\rho _h\Phi '(\eta _{h, j}) = \prod _{j=1}^{h}(\rho +O(B_2^h))(\Phi '(\eta _j)+O(B_2^h)) = \rho ^h (1 + O(hB_2^h))\prod _{j=1}^h\Phi '(\eta _j). \end{align*}
\begin{align*} \prod _{j=1}^{h}\rho _h\Phi '(\eta _{h, j}) = \prod _{j=1}^{h}(\rho +O(B_2^h))(\Phi '(\eta _j)+O(B_2^h)) = \rho ^h (1 + O(hB_2^h))\prod _{j=1}^h\Phi '(\eta _j). \end{align*}
Since
![]() $\Phi '(\eta _j) = \Phi '(0) + O(\zeta ^j)$
(by Lemma 4.3), the product that defines
$\Phi '(\eta _j) = \Phi '(0) + O(\zeta ^j)$
(by Lemma 4.3), the product that defines
![]() $\lambda _2$
converges. So we can rewrite the product term as
$\lambda _2$
converges. So we can rewrite the product term as
 \begin{equation*} \prod _{j=1}^h\Phi '(\eta _j) = \Phi '(0)^h \prod _{j=1}^h\frac {\Phi '(\eta _j)}{\Phi '(0)} = \lambda _2 \Phi '(0)^h \prod _{j\geq h+1}\frac {\Phi '(0)}{\Phi '(\eta _j)}, \end{equation*}
\begin{equation*} \prod _{j=1}^h\Phi '(\eta _j) = \Phi '(0)^h \prod _{j=1}^h\frac {\Phi '(\eta _j)}{\Phi '(0)} = \lambda _2 \Phi '(0)^h \prod _{j\geq h+1}\frac {\Phi '(0)}{\Phi '(\eta _j)}, \end{equation*}
and thus, using again the estimate
![]() $\Phi '(\eta _j) = \Phi '(0) + O(\zeta ^j)$
on the remaining product,
$\Phi '(\eta _j) = \Phi '(0) + O(\zeta ^j)$
on the remaining product,
 \begin{align*} \prod _{j=1}^{h}\rho _h\Phi '(\eta _{h, j}) & = \lambda _2 \zeta ^h (1 + O(hB_2^h))(1+O(\zeta ^h)). \end{align*}
\begin{align*} \prod _{j=1}^{h}\rho _h\Phi '(\eta _{h, j}) & = \lambda _2 \zeta ^h (1 + O(hB_2^h))(1+O(\zeta ^h)). \end{align*}
This proves the desired formula for a suitable choice of
![]() $B_3$
.
$B_3$
.
Corollary 4.5.
For sufficiently large
![]() $h$
, we have that
$h$
, we have that
where
![]() $\lambda _2$
and
$\lambda _2$
and
![]() $B_3$
are as in Lemma 4.4
.
$B_3$
are as in Lemma 4.4
.
Proof. Taking the asymptotic formulas from the statement of Lemma 4.4 and applying them to (47) we obtain the formula after solving for
![]() $\rho _h\Phi '(\eta _{h, 0})$
.
$\rho _h\Phi '(\eta _{h, 0})$
.
In the proof of Lemma 4.2 we used the bound
![]() $\eta _{h, h} = O(B_1^h)$
(obtained from Lemma 4.1). In order to refine the process, we need a more precise estimate.
$\eta _{h, h} = O(B_1^h)$
(obtained from Lemma 4.1). In order to refine the process, we need a more precise estimate.
Lemma 4.6.
For sufficiently large
![]() $h$
and a fixed constant
$h$
and a fixed constant
![]() $B_4 \lt 1$
, we have that
$B_4 \lt 1$
, we have that
where
![]() $\lambda _1$
is as defined in Lemma 4.3
.
$\lambda _1$
is as defined in Lemma 4.3
.
Proof. Pick some
![]() $\alpha \in (0,1)$
in such a way that
$\alpha \in (0,1)$
in such a way that
![]() $\zeta ^{\alpha } \gt B_2$
, with
$\zeta ^{\alpha } \gt B_2$
, with
![]() $B_2$
as in Lemma 4.2, and set
$B_2$
as in Lemma 4.2, and set
![]() $m = \lfloor \alpha h \rfloor$
. From Lemma 4.3, we know that
$m = \lfloor \alpha h \rfloor$
. From Lemma 4.3, we know that
![]() $\eta _m = \Theta ( \zeta ^{\alpha h})$
. By Lemma 4.2,
$\eta _m = \Theta ( \zeta ^{\alpha h})$
. By Lemma 4.2,
![]() $\eta _{h,m} = \eta _m + O(B_2^h)$
, so by our choice of
$\eta _{h,m} = \eta _m + O(B_2^h)$
, so by our choice of
![]() $\alpha$
there is some
$\alpha$
there is some
![]() $B_4 \lt 1$
such that
$B_4 \lt 1$
such that
![]() $\eta _{h,m} = \eta _m (1 + O(B_4^h))$
for sufficiently large
$\eta _{h,m} = \eta _m (1 + O(B_4^h))$
for sufficiently large
![]() $h$
.
$h$
.
Next, recall from (46) that
By the mean value theorem, there is some
![]() $\xi _{h,k} \in (\eta _{h,h},\eta _{h,k-1})$
such that
$\xi _{h,k} \in (\eta _{h,h},\eta _{h,k-1})$
such that
Assume now that
![]() $k \geq m$
, so that
$k \geq m$
, so that
![]() $\eta _{h,k-1} = O(B_1^{\alpha h})$
by Lemma 4.1. Moreover,
$\eta _{h,k-1} = O(B_1^{\alpha h})$
by Lemma 4.1. Moreover,
![]() $\rho _h = \rho + O(B_2^h)$
by Lemma 4.2. So with
$\rho _h = \rho + O(B_2^h)$
by Lemma 4.2. So with
![]() $B = \max\! (B_2,B_1^{\alpha })$
, it follows that
$B = \max\! (B_2,B_1^{\alpha })$
, it follows that
uniformly for all
![]() $k \geq m$
. Rewrite this as
$k \geq m$
. Rewrite this as
Iterate this
![]() $h-m$
times to obtain
$h-m$
times to obtain
 \begin{align*} \eta _{h,m} &= \sum _{j=0}^{h-m} \frac{\eta _{h,h}}{\zeta ^j} (1 + O(B^h))^j \\ &= \eta _{h,h} \zeta ^{-(h-m)} \frac{1 - \zeta ^{h-m+1}}{1-\zeta } (1 + O(h B^h)). \end{align*}
\begin{align*} \eta _{h,m} &= \sum _{j=0}^{h-m} \frac{\eta _{h,h}}{\zeta ^j} (1 + O(B^h))^j \\ &= \eta _{h,h} \zeta ^{-(h-m)} \frac{1 - \zeta ^{h-m+1}}{1-\zeta } (1 + O(h B^h)). \end{align*}
Now recall that
![]() $\eta _{h,m} = \eta _m (1 + O(B_4^h))$
, and that
$\eta _{h,m} = \eta _m (1 + O(B_4^h))$
, and that
![]() $\eta _m = \lambda _1 \zeta ^m (1 + O(B_1^{\alpha h}))$
by Lemma 4.3. Plugging all this in and solving for
$\eta _m = \lambda _1 \zeta ^m (1 + O(B_1^{\alpha h}))$
by Lemma 4.3. Plugging all this in and solving for
![]() $\eta _{h,h}$
, we obtain (49), provided that
$\eta _{h,h}$
, we obtain (49), provided that
![]() $B_4$
was also chosen to be greater than
$B_4$
was also chosen to be greater than
![]() $B$
and
$B$
and
![]() $\zeta ^{1-\alpha }$
.
$\zeta ^{1-\alpha }$
.
Now we can make use of this asymptotic formula for
![]() $\eta _{h,h}$
in order to obtain a refined estimate for
$\eta _{h,h}$
in order to obtain a refined estimate for
![]() $\eta _{h, 0}$
.
$\eta _{h, 0}$
.
Proposition 4.7.
For a fixed constant
![]() $B_5 \lt 1$
and large enough
$B_5 \lt 1$
and large enough
![]() $h$
, we have that
$h$
, we have that
and
where
![]() $\lambda _1$
and
$\lambda _1$
and
![]() $\lambda _2$
are as in Lemmata 4.3 and 4.4 respectively.
$\lambda _2$
are as in Lemmata 4.3 and 4.4 respectively.
Proof. From (45) and (46) with
![]() $k = 1$
, we have
$k = 1$
, we have
By means of Taylor expansion and Lemma 4.6, we get
We multiply this by (48) and divide through by
![]() $\rho _h$
to obtain
$\rho _h$
to obtain
or, with
![]() $H(x) = x\Phi '(x) - \Phi (x)$
,
$H(x) = x\Phi '(x) - \Phi (x)$
,
We plug in the asymptotic formula for
![]() $\eta _{h,h}$
from Lemma 4.6 and also note that
$\eta _{h,h}$
from Lemma 4.6 and also note that
![]() $\Phi (\eta _{h,0}) = \Phi (\tau + O(B_2^h)) = \Phi (\tau ) + O(B_2^h)$
by Lemma 4.2. This gives us
$\Phi (\eta _{h,0}) = \Phi (\tau + O(B_2^h)) = \Phi (\tau ) + O(B_2^h)$
by Lemma 4.2. This gives us
where
![]() $B_5 = \max\! (\zeta,B_2,B_3,B_4)$
. Now note that the function
$B_5 = \max\! (\zeta,B_2,B_3,B_4)$
. Now note that the function
![]() $H$
is increasing (on the positive real numbers within the radius of convergence of
$H$
is increasing (on the positive real numbers within the radius of convergence of
![]() $\Phi$
) with derivative
$\Phi$
) with derivative
![]() $H'(x) = x \Phi ''(x)$
and a unique zero at
$H'(x) = x \Phi ''(x)$
and a unique zero at
![]() $\tau$
. So by inverting (54), we finally end up with
$\tau$
. So by inverting (54), we finally end up with
completing the proof of the first formula. Now we return to (48), which gives us
Plugging in (50) and simplifying by means of the identities
![]() $\rho \Phi (\tau ) = \tau$
and
$\rho \Phi (\tau ) = \tau$
and
![]() $\rho \Phi '(\tau ) = 1$
now yields (51).
$\rho \Phi '(\tau ) = 1$
now yields (51).
4.2 Proof of Theorem 1.2
We are now finally ready to apply Theorems 2.1 and 2.2. The generating functions
![]() $Y_h(z) \,{:\!=}\, Y_{h,0}(z) = Y_{h,1}(z) + z$
were defined precisely in such a way that
$Y_h(z) \,{:\!=}\, Y_{h,0}(z) = Y_{h,1}(z) + z$
were defined precisely in such a way that
![]() $y_{h,n} = [z^n] Y_h(z)$
is the number of
$y_{h,n} = [z^n] Y_h(z)$
is the number of
![]() $n$
-vertex trees for which the maximum protection number is less than or equal to
$n$
-vertex trees for which the maximum protection number is less than or equal to
![]() $h$
. Thus the random variable
$h$
. Thus the random variable
![]() $X_n$
in Theorem 2.1 becomes the maximum protection number of a random
$X_n$
in Theorem 2.1 becomes the maximum protection number of a random
![]() $n$
-vertex tree. Condition (2) of Theorem 2.1 is satisfied in view of Proposition 3.16. Condition (1) holds by Proposition 4.7 with
$n$
-vertex tree. Condition (2) of Theorem 2.1 is satisfied in view of Proposition 3.16. Condition (1) holds by Proposition 4.7 with
![]() $\zeta = \rho \Phi '(0)$
and
$\zeta = \rho \Phi '(0)$
and
where
![]() $\lambda _1$
is as defined in Lemma 4.3 and we recall the definition of
$\lambda _1$
is as defined in Lemma 4.3 and we recall the definition of
![]() $\zeta$
as
$\zeta$
as
![]() $\rho \Phi '(0)$
. This already proves the first part of Theorem 1.2.
$\rho \Phi '(0)$
. This already proves the first part of Theorem 1.2.
We can also apply Theorem 2.2: Note that the maximum protection number of a tree with size
![]() $n$
is no greater than
$n$
is no greater than
![]() $n-1$
, thus
$n-1$
, thus
![]() $y_{h, n} = y_n$
for
$y_{h, n} = y_n$
for
![]() $h \geq n-1$
, and an appropriate choice of constant for Condition (1) in Theorem 2.2 would be
$h \geq n-1$
, and an appropriate choice of constant for Condition (1) in Theorem 2.2 would be
![]() $K = 1$
. Conditions (2) and (3) are still covered by Proposition 3.16. Hence Theorem 2.2 applies, and the second part of Theorem 1.2 follows.
$K = 1$
. Conditions (2) and (3) are still covered by Proposition 3.16. Hence Theorem 2.2 applies, and the second part of Theorem 1.2 follows.
5. The double-exponential case:
 $w_1 = 0$
$w_1 = 0$
5.1 Asymptotics of the singularities
In Section 4.1, it was crucial in most of our asymptotic estimates that
![]() $w_1 = \Phi '(0) \neq 0$
. In this section we assume that
$w_1 = \Phi '(0) \neq 0$
. In this section we assume that
![]() $w_1 = \Phi '(0) = 0$
and define
$w_1 = \Phi '(0) = 0$
and define
![]() $r$
to be the smallest positive outdegree with nonzero weight:
$r$
to be the smallest positive outdegree with nonzero weight:
Our goal will be to determine the asymptotic behaviour of
![]() $\rho _h$
in this case, based again on the system of equations that is given by (45), (46) and (47). Once again,
$\rho _h$
in this case, based again on the system of equations that is given by (45), (46) and (47). Once again,
![]() $B_i$
’s will always denote positive constants with
$B_i$
’s will always denote positive constants with
![]() $B_i \lt 1$
(different from those in the previous section, but for simplicity we restart the count at
$B_i \lt 1$
(different from those in the previous section, but for simplicity we restart the count at
![]() $B_1$
) that depend on the specific family of simply generated trees, but nothing else.
$B_1$
) that depend on the specific family of simply generated trees, but nothing else.
No part of the proof of Lemma 4.1 depends on
![]() $\Phi '(0) \neq 0$
and thus it also holds in the case which we are currently working in, so we already have an exponential bound on
$\Phi '(0) \neq 0$
and thus it also holds in the case which we are currently working in, so we already have an exponential bound on
![]() $\eta _{h,k}$
. However, this bound is loose if
$\eta _{h,k}$
. However, this bound is loose if
![]() $\Phi '(0) = 0$
, and so we determine a tighter bound.
$\Phi '(0) = 0$
, and so we determine a tighter bound.
Lemma 5.1.
There exist positive constants
![]() $C$
and
$C$
and
![]() $B_1$
with
$B_1$
with
![]() $B_1 \lt 1$
such that
$B_1 \lt 1$
such that
![]() $\eta _{h,k} \leq C B_1^{r^k}$
for all sufficiently large
$\eta _{h,k} \leq C B_1^{r^k}$
for all sufficiently large
![]() $h$
and all
$h$
and all
![]() $k$
with
$k$
with
![]() $0 \leq k \leq h$
.
$0 \leq k \leq h$
.
Proof. From (46), we have that
![]() $\eta _{h, k} = \rho _h\Phi (\eta _{h, k-1}) - \rho _h\Phi (\eta _{h, h})$
. Using the Taylor expansion about 0, this gives, for some
$\eta _{h, k} = \rho _h\Phi (\eta _{h, k-1}) - \rho _h\Phi (\eta _{h, h})$
. Using the Taylor expansion about 0, this gives, for some
![]() $\xi _{h, k-1} \in (0, \eta _{h, k-1})$
,
$\xi _{h, k-1} \in (0, \eta _{h, k-1})$
,
 \begin{align*} \eta _{h, k} &= \rho _h\Big (\Phi (0) + \frac{\Phi ^{(r)}(\xi _{h, k-1})}{r!}\eta _{h, k-1}^r\Big ) - \rho _h\Phi (\eta _{h, h}) \\ &\leq \rho _h \frac{\Phi ^{(r)}(\xi _{h, k-1})}{r!}\eta _{h, k-1}^r \leq \rho _h \frac{\Phi ^{(r)}(\eta _{h, 1})}{r!}\eta _{h, k-1}^r. \end{align*}
\begin{align*} \eta _{h, k} &= \rho _h\Big (\Phi (0) + \frac{\Phi ^{(r)}(\xi _{h, k-1})}{r!}\eta _{h, k-1}^r\Big ) - \rho _h\Phi (\eta _{h, h}) \\ &\leq \rho _h \frac{\Phi ^{(r)}(\xi _{h, k-1})}{r!}\eta _{h, k-1}^r \leq \rho _h \frac{\Phi ^{(r)}(\eta _{h, 1})}{r!}\eta _{h, k-1}^r. \end{align*}
There is a constant
![]() $M$
such that
$M$
such that
![]() $\rho _h \frac{\Phi ^{(r)}(\eta _{h, 1})}{r!} \leq M$
for all sufficiently large
$\rho _h \frac{\Phi ^{(r)}(\eta _{h, 1})}{r!} \leq M$
for all sufficiently large
![]() $h$
, since we already know that
$h$
, since we already know that
![]() $\rho _h$
and
$\rho _h$
and
![]() $\eta _{h,1}$
converge. So for sufficiently large
$\eta _{h,1}$
converge. So for sufficiently large
![]() $h$
, we have
$h$
, we have
![]() $\eta _{h, k} \leq M \eta _{h,k-1}^r$
for all
$\eta _{h, k} \leq M \eta _{h,k-1}^r$
for all
![]() $k \gt 1$
. Iterating this inequality yields
$k \gt 1$
. Iterating this inequality yields
for
![]() $0\le \ell \le k$
. In view of the exponential bound on
$0\le \ell \le k$
. In view of the exponential bound on
![]() $\eta _{h,\ell }$
provided by Lemma 4.1, we can choose
$\eta _{h,\ell }$
provided by Lemma 4.1, we can choose
![]() $\ell$
so large that
$\ell$
so large that
![]() $M^{1/(r-1)} \eta _{h,\ell } \leq \frac 12$
for all sufficiently large
$M^{1/(r-1)} \eta _{h,\ell } \leq \frac 12$
for all sufficiently large
![]() $h$
. This proves the desired bound for
$h$
. This proves the desired bound for
![]() $k \geq \ell$
with
$k \geq \ell$
with
![]() $B_1 = 2^{-r^{-\ell }}$
and a suitable choice of
$B_1 = 2^{-r^{-\ell }}$
and a suitable choice of
![]() $C$
(for
$C$
(for
![]() $k \lt \ell$
, it is implied by the exponential bound).
$k \lt \ell$
, it is implied by the exponential bound).
Our next step is an analogue of Lemma 4.4.
Lemma 5.2.
For large enough
![]() $h$
and the same constant
$h$
and the same constant
![]() $B_1 \lt 1$
as in the previous lemma, we have
$B_1 \lt 1$
as in the previous lemma, we have
 \begin{equation*} 1 + \sum _{k = 2}^{h}\prod _{j = k}^{h} (\rho _h \Phi '(\eta _{h, j})) = 1 + O(B_1^{r^h}) \end{equation*}
\begin{equation*} 1 + \sum _{k = 2}^{h}\prod _{j = k}^{h} (\rho _h \Phi '(\eta _{h, j})) = 1 + O(B_1^{r^h}) \end{equation*}
and
 \begin{equation*} \prod _{j=1}^{h}\rho _h\Phi '(\eta _{h, j}) = O(B_1^{r^h}). \end{equation*}
\begin{equation*} \prod _{j=1}^{h}\rho _h\Phi '(\eta _{h, j}) = O(B_1^{r^h}). \end{equation*}
Proof. We already know that
![]() $\rho _h \Phi '(\eta _{h,1})$
converges to
$\rho _h \Phi '(\eta _{h,1})$
converges to
![]() $\rho \Phi '(\tau - \rho ) \lt 1$
, so for sufficiently large
$\rho \Phi '(\tau - \rho ) \lt 1$
, so for sufficiently large
![]() $h$
and some
$h$
and some
![]() $q \lt 1$
, we have
$q \lt 1$
, we have
![]() $\rho _h\Phi '(\eta _{h, j}) \leq \rho _h \Phi '(\eta _{h,1}) \leq q$
for all
$\rho _h\Phi '(\eta _{h, j}) \leq \rho _h \Phi '(\eta _{h,1}) \leq q$
for all
![]() $j \geq 1$
. It follows that
$j \geq 1$
. It follows that
 \begin{equation*} \sum _{k = 2}^{h}\prod _{j = k}^{h} (\rho _h \Phi '(\eta _{h, j})) \leq \sum _{k=2}^h q^{h-k} \rho _h \Phi '(\eta _{h,h}) \leq \frac {1}{1-q} \rho _h \Phi '(\eta _{h,h}) \end{equation*}
\begin{equation*} \sum _{k = 2}^{h}\prod _{j = k}^{h} (\rho _h \Phi '(\eta _{h, j})) \leq \sum _{k=2}^h q^{h-k} \rho _h \Phi '(\eta _{h,h}) \leq \frac {1}{1-q} \rho _h \Phi '(\eta _{h,h}) \end{equation*}
and
 \begin{equation*} \prod _{j=1}^{h}\rho _h\Phi '(\eta _{h, j}) \leq q^{h-1} \rho _h \Phi '(\eta _{h,h}). \end{equation*}
\begin{equation*} \prod _{j=1}^{h}\rho _h\Phi '(\eta _{h, j}) \leq q^{h-1} \rho _h \Phi '(\eta _{h,h}). \end{equation*}
Now both statements follow from the fact that
![]() $\Phi '(\eta _{h,h}) = \Phi '(0) + O(\eta _{h,h}) = O(\eta _{h,h})$
and the previous lemma.
$\Phi '(\eta _{h,h}) = \Phi '(0) + O(\eta _{h,h}) = O(\eta _{h,h})$
and the previous lemma.
Taking the results from Lemma 5.2 and applying them to (47), we find that
Additionally note that using Lemma 5.1 and Taylor expansion, we have that
Now recall that (45) and (46) yield (see (52))
which now becomes
Taking advantage of the expressions in (56) and (58), we can now prove doubly exponential convergence of
![]() $\rho _h$
and
$\rho _h$
and
![]() $\eta _{h, 0}$
(using the approach of Proposition 4.7).
$\eta _{h, 0}$
(using the approach of Proposition 4.7).
Lemma 5.3.
For large enough
![]() $h$
, it holds that
$h$
, it holds that
and thus also
![]() $\eta _{h,1} = \eta _{h,0} - \rho _h = \eta _1 + O(B_1^{r^h})$
.
$\eta _{h,1} = \eta _{h,0} - \rho _h = \eta _1 + O(B_1^{r^h})$
.
Proof. Multiplying (56) and (58) and dividing by
![]() $\rho _h$
yields
$\rho _h$
yields
As in the proof of Proposition 4.7, we observe that the function
![]() $H(x) = x \Phi '(x) - \Phi (x)$
is increasing (on the positive real numbers within the radius of convergence of
$H(x) = x \Phi '(x) - \Phi (x)$
is increasing (on the positive real numbers within the radius of convergence of
![]() $\Phi$
) with derivative
$\Phi$
) with derivative
![]() $H'(x) = x \Phi ''(x)$
and a unique zero at
$H'(x) = x \Phi ''(x)$
and a unique zero at
![]() $\tau$
. So it follows from this equation that
$\tau$
. So it follows from this equation that
![]() $\eta _{h, 0} = \tau + O\big (B_1^{r^{h}}\big )$
. Using this estimate for
$\eta _{h, 0} = \tau + O\big (B_1^{r^{h}}\big )$
. Using this estimate for
![]() $\eta _{h, 0}$
in (56) it follows that
$\eta _{h, 0}$
in (56) it follows that
![]() $\rho _h = \rho + O\big (B_1^{r^{h}}\big )$
.
$\rho _h = \rho + O\big (B_1^{r^{h}}\big )$
.
As in the previous section, we will approximate
![]() $\eta _{h,k}$
by
$\eta _{h,k}$
by
![]() $\eta _k$
, defined recursively by
$\eta _k$
, defined recursively by
![]() $\eta _0 = \tau$
and
$\eta _0 = \tau$
and
![]() $\eta _k = \rho (\Phi (\eta _{k-1}) - 1)$
. As it turns out, this approximation is even more precise in the current case.
$\eta _k = \rho (\Phi (\eta _{k-1}) - 1)$
. As it turns out, this approximation is even more precise in the current case.
Lemma 5.4.
For a fixed constant
![]() $B_2 \lt 1$
and sufficiently large
$B_2 \lt 1$
and sufficiently large
![]() $h$
, we have that
$h$
, we have that
uniformly for all
![]() $0 \leq k \leq h$
.
$0 \leq k \leq h$
.
Proof. Recall that, by (46),
![]() $\eta _{h, k} = \rho _h\Phi (\eta _{h, k-1}) - \rho _h\Phi (\eta _{h, h})$
. By Taylor expansion, we find that
$\eta _{h, k} = \rho _h\Phi (\eta _{h, k-1}) - \rho _h\Phi (\eta _{h, h})$
. By Taylor expansion, we find that
Since
![]() $\eta _{h,k} \geq \eta _{h,h}$
, we have
$\eta _{h,k} \geq \eta _{h,h}$
, we have
![]() $\eta _{h,k} - O(\eta _{h,h}^r) = \eta _{h,k} (1 - O(\eta _{h,h}^{r-1}))$
. Now we use the estimates
$\eta _{h,k} - O(\eta _{h,h}^r) = \eta _{h,k} (1 - O(\eta _{h,h}^{r-1}))$
. Now we use the estimates
![]() $\eta _{h,h} = O(B_1^{r^h})$
from Lemma 5.1 and
$\eta _{h,h} = O(B_1^{r^h})$
from Lemma 5.1 and
![]() $\rho _h = \rho + O(B_1^{r^h})$
from Lemma 5.3 to obtain
$\rho _h = \rho + O(B_1^{r^h})$
from Lemma 5.3 to obtain
We compare this to
Taking the logarithm in both these equations and subtracting yields
For large enough
![]() $h$
, we can assume that
$h$
, we can assume that
![]() $\eta _{h,1} \leq \tau$
and thus
$\eta _{h,1} \leq \tau$
and thus
![]() $\eta _{h,k} \leq \tau$
for all
$\eta _{h,k} \leq \tau$
for all
![]() $k \geq 1$
. The auxiliary function
$k \geq 1$
. The auxiliary function
is continuously differentiable on
![]() $(-\infty,\log (\tau )]$
. Since
$(-\infty,\log (\tau )]$
. Since
![]() $\lim _{u \to -\infty } \Psi _1^{\prime}(u) = r$
, as one easily verifies,
$\lim _{u \to -\infty } \Psi _1^{\prime}(u) = r$
, as one easily verifies,
![]() $|{\Psi _1^{\prime}(u)}|$
must be bounded by some constant
$|{\Psi _1^{\prime}(u)}|$
must be bounded by some constant
![]() $K$
for all
$K$
for all
![]() $u$
in this interval, thus
$u$
in this interval, thus
![]() $|{\Psi _1(u+v) - \Psi _1(u)}| \leq K|v|$
whenever
$|{\Psi _1(u+v) - \Psi _1(u)}| \leq K|v|$
whenever
![]() $u,u+v \leq \log\! (\tau )$
. We apply this with
$u,u+v \leq \log\! (\tau )$
. We apply this with
![]() $u+v = \log \eta _{h,k-1}$
and
$u+v = \log \eta _{h,k-1}$
and
![]() $u = \log \eta _{k-1}$
to obtain
$u = \log \eta _{k-1}$
to obtain
Plugging this into (59) yields
We already know that
![]() $\big | \log \frac{\eta _{h,0}}{\eta _0} \big | = O(B_1^{r^h})$
and
$\big | \log \frac{\eta _{h,0}}{\eta _0} \big | = O(B_1^{r^h})$
and
![]() $\big | \log \frac{\eta _{h,1}}{\eta _1} \big | = O(B_1^{r^h})$
in view of Lemma 5.3. Iterating (60) gives us
$\big | \log \frac{\eta _{h,1}}{\eta _1} \big | = O(B_1^{r^h})$
in view of Lemma 5.3. Iterating (60) gives us
which implies the statement for any
![]() $B_2 \gt B_1$
.
$B_2 \gt B_1$
.
The next lemma parallels Lemma 4.3.
Lemma 5.5.
There exist positive constants
![]() $\lambda _1$
and
$\lambda _1$
and
![]() $\mu \lt 1$
such that
$\mu \lt 1$
such that
with the same constant
![]() $B_1$
as in Lemma 5.1
.
$B_1$
as in Lemma 5.1
.
Proof. Note that Lemma 5.1 trivially implies that
![]() $\eta _k=O(B_1^{r^k})$
. From the recursion
$\eta _k=O(B_1^{r^k})$
. From the recursion
we obtain, by the properties of
![]() $\Phi$
,
$\Phi$
,
Set
and divide both sides by
![]() $\lambda _1$
to obtain
$\lambda _1$
to obtain
Let us write
![]() $e^{\theta _{k-1}}$
for the final factor, where
$e^{\theta _{k-1}}$
for the final factor, where
![]() $\theta _{k-1} = O(\eta _{k-1})$
. Taking the logarithm yields
$\theta _{k-1} = O(\eta _{k-1})$
. Taking the logarithm yields
We iterate this recursion
![]() $k$
times to obtain
$k$
times to obtain
 \begin{align*} \log \frac{\eta _k}{\lambda _1} &= r^k \log \frac{\eta _0}{\lambda _1} + \sum _{j=0}^{k-1} r^{k-1-j} \theta _j \\ &= r^k \Big ( \log \frac{\eta _0}{\lambda _1} + \sum _{j=0}^{\infty } r^{-1-j} \theta _j \Big ) - \sum _{j=k}^{\infty } r^{k-1-j} \theta _j. \end{align*}
\begin{align*} \log \frac{\eta _k}{\lambda _1} &= r^k \log \frac{\eta _0}{\lambda _1} + \sum _{j=0}^{k-1} r^{k-1-j} \theta _j \\ &= r^k \Big ( \log \frac{\eta _0}{\lambda _1} + \sum _{j=0}^{\infty } r^{-1-j} \theta _j \Big ) - \sum _{j=k}^{\infty } r^{k-1-j} \theta _j. \end{align*}
The infinite series converge in view of the estimate
![]() $\theta _j = O(\eta _j) = O(B_1^{r^j})$
that we get from Lemma 5.1. Moreover, we have
$\theta _j = O(\eta _j) = O(B_1^{r^j})$
that we get from Lemma 5.1. Moreover, we have
![]() $\sum _{j=k}^{\infty } r^{k-1-j} \theta _j = O(B_1^{r^k})$
by the same bound. The result follows upon taking the exponential on both sides and multiplying by
$\sum _{j=k}^{\infty } r^{k-1-j} \theta _j = O(B_1^{r^k})$
by the same bound. The result follows upon taking the exponential on both sides and multiplying by
![]() $\lambda _1$
, setting
$\lambda _1$
, setting
 \begin{equation} \mu \,{:\!=}\, \exp \Big ( \log \frac{\eta _0}{\lambda _1} + \sum _{j=0}^{\infty } r^{-1-j} \theta _j \Big ) = \frac{\eta _0}{\lambda _1} \prod _{j=0}^{\infty } e^{\theta _j/r^{j+1}}. \end{equation}
\begin{equation} \mu \,{:\!=}\, \exp \Big ( \log \frac{\eta _0}{\lambda _1} + \sum _{j=0}^{\infty } r^{-1-j} \theta _j \Big ) = \frac{\eta _0}{\lambda _1} \prod _{j=0}^{\infty } e^{\theta _j/r^{j+1}}. \end{equation}
Note that
![]() $\mu \lt 1$
because we already know that
$\mu \lt 1$
because we already know that
![]() $\eta _k=O(B_1^{r^k})$
.
$\eta _k=O(B_1^{r^k})$
.
In order to further analyse the behaviour of the product
![]() $\prod _{j = 1}^h (\rho _h \Phi '(\eta _{h, j}))$
in (47), we need one more short lemma.
$\prod _{j = 1}^h (\rho _h \Phi '(\eta _{h, j}))$
in (47), we need one more short lemma.
Lemma 5.6.
For sufficiently large
![]() $h$
, we have that
$h$
, we have that
uniformly for all
![]() $1 \leq k \leq h$
, with the same constant
$1 \leq k \leq h$
, with the same constant
![]() $B_2$
as in Lemma 5.4
.
$B_2$
as in Lemma 5.4
.
Proof. Again, we can assume that
![]() $h$
is so large that
$h$
is so large that
![]() $\eta _{h,k} \leq \tau$
for all
$\eta _{h,k} \leq \tau$
for all
![]() $k \geq 1$
. The auxiliary function
$k \geq 1$
. The auxiliary function
![]() $\Psi _2(u) = \log\! (\Phi '(e^u))$
is continuously differentiable on
$\Psi _2(u) = \log\! (\Phi '(e^u))$
is continuously differentiable on
![]() $(-\infty,\log \tau ]$
and satisfies
$(-\infty,\log \tau ]$
and satisfies
![]() $\lim _{u \to -\infty } \Psi _2^{\prime}(u) = r-1$
. Thus its derivative is also bounded, and the same argument as in Lemma 5.4 shows that
$\lim _{u \to -\infty } \Psi _2^{\prime}(u) = r-1$
. Thus its derivative is also bounded, and the same argument as in Lemma 5.4 shows that
for some positive constant
![]() $K$
. Now the statement follows from Lemma 5.4.
$K$
. Now the statement follows from Lemma 5.4.
Lemma 5.7.
There exist positive constants
![]() $\lambda _2,\lambda _3$
and
$\lambda _2,\lambda _3$
and
![]() $B_3 \lt 1$
such that, for large enough
$B_3 \lt 1$
such that, for large enough
![]() $h$
,
$h$
,
 \begin{equation} \prod _{j = 1}^h (\rho _h \Phi '(\eta _{h, j})) = \lambda _2 \lambda _3^h\mu ^{r^{h+1}} \big (1 + O(B_3^{r^h})\big ), \end{equation}
\begin{equation} \prod _{j = 1}^h (\rho _h \Phi '(\eta _{h, j})) = \lambda _2 \lambda _3^h\mu ^{r^{h+1}} \big (1 + O(B_3^{r^h})\big ), \end{equation}
with
![]() $\mu$
as in Lemma 5.5
.
$\mu$
as in Lemma 5.5
.
Proof. First, observe that
 \begin{equation*} \prod _{j = 1}^h (\rho _h \Phi '(\eta _{h, j})) = \Big (\rho \big (1 + O(B_1^{r^h})\big ) \Big )^h \prod _{j=1}^h \Big ( \Phi '(\eta _j) \big (1 + O(B_2^{r^h})\big)\Big ) = \rho ^h \Big ( \prod _{j=1}^h \Phi '(\eta _j) \Big ) \big (1 + O(h B_2^{r^h})\big ) \end{equation*}
\begin{equation*} \prod _{j = 1}^h (\rho _h \Phi '(\eta _{h, j})) = \Big (\rho \big (1 + O(B_1^{r^h})\big ) \Big )^h \prod _{j=1}^h \Big ( \Phi '(\eta _j) \big (1 + O(B_2^{r^h})\big)\Big ) = \rho ^h \Big ( \prod _{j=1}^h \Phi '(\eta _j) \Big ) \big (1 + O(h B_2^{r^h})\big ) \end{equation*}
in view of Lemmata 5.3 and 5.6 (recall that
![]() $B_2 \gt B_1$
). Next, Taylor expansion combined with Lemma 5.5 gives us
$B_2 \gt B_1$
). Next, Taylor expansion combined with Lemma 5.5 gives us
Set
![]() $\lambda _3 \,{:\!=}\, \rho \frac{\Phi ^{(r)}(0)\lambda _1^{r-1}}{(r-1)!} = rw_r \rho \lambda _1^{r-1}$
, so that
$\lambda _3 \,{:\!=}\, \rho \frac{\Phi ^{(r)}(0)\lambda _1^{r-1}}{(r-1)!} = rw_r \rho \lambda _1^{r-1}$
, so that
It follows that the infinite product
 \begin{equation*} \Pi \,{:\!=}\, \prod _{j = 1}^{\infty } \frac {\rho \Phi '(\eta _j)}{\lambda _3 \mu ^{(r-1)r^j}} \end{equation*}
\begin{equation*} \Pi \,{:\!=}\, \prod _{j = 1}^{\infty } \frac {\rho \Phi '(\eta _j)}{\lambda _3 \mu ^{(r-1)r^j}} \end{equation*}
converges, and that
 \begin{equation*} \prod _{j = 1}^{h} \frac {\rho \Phi '(\eta _j)}{\lambda _3 \mu ^{(r-1)r^j}} = \Pi \big (1 + O(B_1^{r^h})\big ). \end{equation*}
\begin{equation*} \prod _{j = 1}^{h} \frac {\rho \Phi '(\eta _j)}{\lambda _3 \mu ^{(r-1)r^j}} = \Pi \big (1 + O(B_1^{r^h})\big ). \end{equation*}
Consequently,
 \begin{equation*} \prod _{j = 1}^{h} \Phi '(\eta _j) = \Pi \Big ( \frac {\lambda _3}{\rho } \Big )^h \mu ^{r^{h+1}-r} \big (1 + O(B_1^{r^h})\big ). \end{equation*}
\begin{equation*} \prod _{j = 1}^{h} \Phi '(\eta _j) = \Pi \Big ( \frac {\lambda _3}{\rho } \Big )^h \mu ^{r^{h+1}-r} \big (1 + O(B_1^{r^h})\big ). \end{equation*}
Putting everything together, the statement of the lemma follows with
![]() $\lambda _2 = \Pi \mu ^{-r}$
and a suitable choice of
$\lambda _2 = \Pi \mu ^{-r}$
and a suitable choice of
![]() $B_3 \gt B_2$
.
$B_3 \gt B_2$
.
With this estimate for the product term in the determinant of the Jacobian (47), and the estimate for the sum term from Lemma 5.2, we can now obtain a better asymptotic formula for
![]() $\rho _h\Phi '(\eta _{h, 0})$
than that which was obtained in (56). For large enough
$\rho _h\Phi '(\eta _{h, 0})$
than that which was obtained in (56). For large enough
![]() $h$
, we have that
$h$
, we have that
For the error term, recall that
![]() $B_1 \lt B_3$
. Moreover, combining Lemmata 5.4 and 5.5 leads to
$B_1 \lt B_3$
. Moreover, combining Lemmata 5.4 and 5.5 leads to
since
![]() $B_2$
was chosen to be greater than
$B_2$
was chosen to be greater than
![]() $B_1$
, which we can apply to (57):
$B_1$
, which we can apply to (57):
 \begin{align} \eta _{h,0} &= \rho _h \big ( \Phi (\eta _{h,0}) - \Phi (\eta _{h, h}) + 1 \big ) \nonumber \\ &= \rho _h \Big ( \Phi (\eta _{h,0}) - \frac{\Phi ^{(r)}(0)}{r!} \eta _{h,h}^r + O(\eta _{h,h}^{r+1}) \Big ) \nonumber \\ &= \rho _h \Big ( \Phi (\eta _{h,0}) - w_r \lambda _1^r \mu ^{r^{h+1}}\big (1 + O(B_3^{r^h})\big ) \Big ) \end{align}
\begin{align} \eta _{h,0} &= \rho _h \big ( \Phi (\eta _{h,0}) - \Phi (\eta _{h, h}) + 1 \big ) \nonumber \\ &= \rho _h \Big ( \Phi (\eta _{h,0}) - \frac{\Phi ^{(r)}(0)}{r!} \eta _{h,h}^r + O(\eta _{h,h}^{r+1}) \Big ) \nonumber \\ &= \rho _h \Big ( \Phi (\eta _{h,0}) - w_r \lambda _1^r \mu ^{r^{h+1}}\big (1 + O(B_3^{r^h})\big ) \Big ) \end{align}
since
![]() $B_3$
was chosen to be greater than
$B_3$
was chosen to be greater than
![]() $B_1$
(and thus also
$B_1$
(and thus also
![]() $\mu$
) and
$\mu$
) and
![]() $B_2$
. As we did earlier to obtain Lemma 5.3, we multiply the two equations (64) and (65) and divide by
$B_2$
. As we did earlier to obtain Lemma 5.3, we multiply the two equations (64) and (65) and divide by
![]() $\rho _h$
to find that
$\rho _h$
to find that
From this, the following result follows now in exactly the same way as Proposition 4.7 follows from (53).
Proposition 5.8.
For large enough
![]() $h$
and a fixed constant
$h$
and a fixed constant
![]() $B_4 \lt 1$
, we have that
$B_4 \lt 1$
, we have that
and
5.2 An adapted general scheme and the proof of Theorem 1.3
In this final section, we will first prove Theorems 1.4 and 1.5. Then, we will be able to put all pieces together and prove Theorem 1.3.
Proof of Theorem 1.4. We apply singularity analysis, and use the uniformity condition to obtain
uniformly in
![]() $h$
as
$h$
as
![]() $n \to \infty$
as well as
$n \to \infty$
as well as
Since in addition
![]() $A_h \to A$
and
$A_h \to A$
and
![]() $\rho _h = \rho (1+ \kappa \zeta ^{r^{h}} + o(\zeta ^{r^{h}}))$
, it holds that
$\rho _h = \rho (1+ \kappa \zeta ^{r^{h}} + o(\zeta ^{r^{h}}))$
, it holds that
 \begin{align*} \frac{y_{h, n}}{y_n} &= \Big (\frac{\rho _h}{\rho }\Big )^{-n}(1+o(1)) = \exp{\big ({-} \kappa n \zeta ^{r^h} +o(n\zeta ^{r^h})\big )}(1+o(1)) \\ &= \exp{\big ({-}\kappa n\zeta ^{r^h}(1+o(1)) + o(1)\big )}. \end{align*}
\begin{align*} \frac{y_{h, n}}{y_n} &= \Big (\frac{\rho _h}{\rho }\Big )^{-n}(1+o(1)) = \exp{\big ({-} \kappa n \zeta ^{r^h} +o(n\zeta ^{r^h})\big )}(1+o(1)) \\ &= \exp{\big ({-}\kappa n\zeta ^{r^h}(1+o(1)) + o(1)\big )}. \end{align*}
Proof of Theorem 1.5. Fix
![]() $\epsilon \gt 0$
. If
$\epsilon \gt 0$
. If
![]() $h \geq m_n + \epsilon = \log _r{\log _d\!(n)} + \epsilon$
, then Theorem 1.4 gives us
$h \geq m_n + \epsilon = \log _r{\log _d\!(n)} + \epsilon$
, then Theorem 1.4 gives us
thus
![]() $X_n \leq h$
with high probability. If
$X_n \leq h$
with high probability. If
![]() $\{m_n\} \leq 1-\epsilon$
, then this is the case for
$\{m_n\} \leq 1-\epsilon$
, then this is the case for
![]() $h = \lceil m_n \rceil$
, otherwise for
$h = \lceil m_n \rceil$
, otherwise for
![]() $h = \lceil m_n \rceil + 1$
. Similarly, if
$h = \lceil m_n \rceil + 1$
. Similarly, if
![]() $h \leq m_n - \epsilon = \log _r{\log _d\!(n)} - \epsilon$
, then Theorem 1.4 gives us
$h \leq m_n - \epsilon = \log _r{\log _d\!(n)} - \epsilon$
, then Theorem 1.4 gives us
thus
![]() $X_n \gt h$
with high probability. If
$X_n \gt h$
with high probability. If
![]() $\{m_n\} \geq \epsilon$
, then this is the case for
$\{m_n\} \geq \epsilon$
, then this is the case for
![]() $h = \lfloor m_n \rfloor$
, otherwise for
$h = \lfloor m_n \rfloor$
, otherwise for
![]() $h = \lfloor m_n \rfloor - 1$
. The statement now follows by combining the two parts.
$h = \lfloor m_n \rfloor - 1$
. The statement now follows by combining the two parts.
Remark 5.9.
As in Remark 3.17
, we indicate the changes which are necessary for the case that the period
![]() $D$
of
$D$
of
![]() $\Phi$
is greater than
$\Phi$
is greater than
![]() $1$
.
$1$
.
Theorem
1.4
only depends on singularity analysis. It is well known (see [10, Remark VI.17]) that singularity analysis simply introduces a factor
![]() $D$
in this situation, and as this factor
$D$
in this situation, and as this factor
![]() $D$
cancels because it occurs both in the asymptotic expansions of
$D$
cancels because it occurs both in the asymptotic expansions of
![]() $Y_{h}$
as well as
$Y_{h}$
as well as
![]() $Y$
, this theorem remains valid for
$Y$
, this theorem remains valid for
![]() $n\equiv 1\pmod D$
.
$n\equiv 1\pmod D$
.
Theorem 1.3 is now an immediate consequence of Theorems 1.4 and 1.5. In analogy to the proof of Theorem 1.2, the analytic conditions on the generating functions are provided by Proposition 3.16. The condition on the asymptotic behaviour of
![]() $\rho _h$
is given by Proposition 5.8 (with
$\rho _h$
is given by Proposition 5.8 (with
![]() $\zeta = \mu ^r$
). Thus the proof of Theorem 1.3 is complete.
$\zeta = \mu ^r$
). Thus the proof of Theorem 1.3 is complete.
Financial support
The research of C. Heuberger and S. J. Selkirk was funded in part by the Austrian Science Fund (FWF) [10.55776/P28466], Analytic Combinatorics: Digits, Automata and Trees and Austrian Science Fund (FWF) [10.55776/DOC78]. S. Wagner was supported by the Knut and Alice Wallenberg Foundation, grant KAW 2017.0112, and the Swedish research council (VR), grant 2022-04030. For open access purposes, the authors have applied a CC BY public copyright license to any author-accepted manuscript version arising from this submission.