Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T23:09:16.587Z Has data issue: false hasContentIssue false
  • English
  • Français

Dirac’s theorem for random regular graphs

Part of: Graph theory

Published online by Cambridge University Press:  28 August 2020

Padraig Condon ,
Alberto Espuny Díaz ,
António Girão ,
Daniela Kühn  and
Deryk Osthus
Padraig Condon
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK
Alberto Espuny Díaz
Affiliation:
Institut für Mathematik, Technische Universität Ilmenau, 98693 Ilmenau, Germany
António Girão*
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK
Daniela Kühn
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK
Deryk Osthus
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a ‘resilience’ version of Dirac’s theorem in the setting of random regular graphs. More precisely, we show that whenever d is sufficiently large compared to 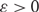$\epsilon > 0$ , a.a.s. the following holds. Let 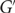$G'$ be any subgraph of the random n-vertex d-regular graph 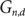$G_{n,d}$ with minimum degree at least 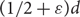$$(1/2 + \epsilon )d$$ . Then 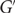$G'$ is Hamiltonian.

This proves a conjecture of Ben-Shimon, Krivelevich and Sudakov. Our result is best possible: firstly the condition that d is large cannot be omitted, and secondly the minimum degree bound cannot be improved.

MSC classification

Primary: 05C80: Random graphs
Secondary: 05C35: Extremal problems 05C45: Eulerian and Hamiltonian graphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 1 , January 2021 , pp. 17 - 36
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

This project has received partial funding from the European Research Council (ERC) under the EuropeanUnion’sHorizon 2020 research and innovation programme (grant agreement 786198, D. Kühn and D. Osthus). The research leading to these results was also partially supported by the EPSRC, grants EP/N019504/1 (A. Girão and D. Kühn) and EP/S00100X/1 (D. Osthus), as well as the Royal Society and theWolfson Foundation (D. Kühn).

References

Ajtai, M., Komlós, J. and Szemerédi, E. (1985) First occurrence of Hamilton cycles in random graphs. In Cycles in Graphs (Burnaby, BC, 1982), Vol. 115 of North-Holland Mathematics Studies, pp. 173–178. North-Holland.Google Scholar
Allen, P., Böttcher, J., Ehrenmüller, J. and Taraz, A. (2020) The bandwidth theorem in sparse graphs. Adv. Combin. 2020. doi: 10.19086/aic.12849 CrossRefGoogle Scholar
Alon, N. and Spencer, J. H. (2016) The Probabilistic Method, Wiley Series in Discrete Mathematics and Optimization. Wiley.Google Scholar
Azuma, K. (1967) Weighted sums of certain dependent random variables. Tôhoku Math. J. (2) 19 357–367.CrossRefGoogle Scholar
Balogh, J., Csaba, B. and Samotij, W. (2011) Local resilience of almost spanning trees in random graphs. Random Struct. Algorithms 38 121–139.Google Scholar
Balogh, J., Lee, C. and Samotij, W. (2012) Corrádi and Hajnal’s theorem for sparse random graphs. Combin. Probab. Comput. 21 23–55.CrossRefGoogle Scholar
Ben-Shimon, S., Krivelevich, M. and Sudakov, B. (2011) Local resilience and Hamiltonicity maker-breaker games in random regular graphs. Combin. Probab. Comput. 20 173–211.CrossRefGoogle Scholar
Ben-Shimon, S., Krivelevich, M. and Sudakov, B. (2011) On the resilience of Hamiltonicity and optimal packing of Hamilton cycles in random graphs. SIAM J. Discrete Math. 25 1176–1193.Google Scholar
Bollobás, B. (1980) A probabilistic proof of an asymptotic formula for the number of labelled regular graphs. European J. Combin. 1 311–316.Google Scholar
Bollobás, B. (1984) The evolution of sparse graphs. In Graph Theory and Combinatorics (Cambridge, 1983), pp. 35–57. Academic Press.Google Scholar
Condon, P., Espuny Díaz, A., Girão, A., Kühn, D. and Osthus, D. (2019) Dirac’s theorem for random regular graphs. arXiv:1903.05052Google Scholar
Condon, P., Espuny Daz, A., Kim, J., Kühn, D. and Osthus, D. (2019) Resilient degree sequences with respect to Hamilton cycles and matchings in random graphs. Electron. J. Combin. 26 4.54.Google Scholar
Cook, N., Goldstein, L. and Johnson, T. (2018) Size biased couplings and the spectral gap for random regular graphs. Ann. Probab. 46 72–125.CrossRefGoogle Scholar
Cooper, C., Frieze, A. and Reed, B. (2002) Random regular graphs of non-constant degree: connectivity and Hamiltonicity. Combin. Probab. Comput. 11 249–261.CrossRefGoogle Scholar
Ferber, A., Nenadov, R., Noever, A., Peter, U. and Škorić, N. (2017) Robust Hamiltonicity of random directed graphs. J. Combin. Theory Ser. B 126 1–23.CrossRefGoogle Scholar
Frieze, A. (2019) Hamilton cycles in random graphs: a bibliography. arXiv:1901.07139Google Scholar
Frieze, A. and Krivelevich, M. (2008) On two Hamilton cycle problems in random graphs. Israel J. Math. 166 221–234.CrossRefGoogle Scholar
Hefetz, D., Steger, A. and Sudakov, B. (2016) Random directed graphs are robustly Hamiltonian. Random Struct. Algorithms 49 345–362.CrossRefGoogle Scholar
Hoeffding, W. (1963) Probability inequalities for sums of bounded random variables. J. Amer. Statist. Assoc. 58 13–30.CrossRefGoogle Scholar
Huang, H., Lee, C. and Sudakov, B. (2012) Bandwidth theorem for random graphs. J. Combin. Theory Ser. B 102 14–37.CrossRefGoogle Scholar
Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley-Interscience Series in Discrete Mathematics and Optimization. Wiley-Interscience.CrossRefGoogle Scholar
Kim, J. H. and Vu, V. H. (2004) Sandwiching random graphs: universality between random graph models. Adv. Math. 188 444–469.CrossRefGoogle Scholar
Komlós, J. and Szemerédi, E. (1983) Limit distribution for the existence of Hamiltonian cycles in a random graph. Discrete Math. 43 55–63.CrossRefGoogle Scholar
Krivelevich, M. (2016) Long paths and Hamiltonicity in random graphs. In Random Graphs, Geometry and Asymptotic Structure (Fountoulakis, N. and Hefetz, D., eds), Vol. 84 of London Mathematical Society Student Texts, pp. 4–27. Cambridge University Press.Google Scholar
Krivelevich, M., Lee, C. and Sudakov, B. (2010) Resilient pancyclicity of random and pseudorandom graphs. SIAM J. Discrete Math. 24 1–16.Google Scholar
Krivelevich, M., Sudakov, B., Vu, V. H. and Wormald, N. C. (2001) Random regular graphs of high degree. Random Struct. Algorithms 18 346–363.CrossRefGoogle Scholar
Lee, C. and Sudakov, B. (2012) Dirac’s theorem for random graphs. Random Struct. Algorithms 41 293–305.Google Scholar
McKay, B. D. (1987) Independent sets in regular graphs of high girth. Ars Combin. 23 179–185.Google Scholar
McKay, B. D. and Wormald, N. C. (1990) Uniform generation of random regular graphs of moderate degree. J. Algorithms 11 52–67.Google Scholar
Montgomery, R. (2019) Hamiltonicity in random graphs is born resilient. J. Combin. Theory Ser. B 139 316–341.CrossRefGoogle Scholar
Montgomery, R. (2020) Hamiltonicity in random directed graphs is born resilient. Combin. Probab. Comput. doi: 10.1017/S0963548320000140.CrossRefGoogle Scholar
Nenadov, R., Steger, A. and Trujić, M. (2019) Resilience of perfect matchings and Hamiltonicity in random graph processes. Random Struct. Algorithms 54 797–819.Google Scholar
Robinson, R. W. and Wormald, N. C. (1992) Almost all cubic graphs are Hamiltonian. Random Struct. Algorithms 3 117–125.CrossRefGoogle Scholar
Robinson, R. W. and Wormald, N. C. (1994) Almost all regular graphs are Hamiltonian. Random Struct. Algorithms 5 363–374.CrossRefGoogle Scholar
Škorić, N., Steger, A. and Trujić, M. (2018) Local resilience of an almost spanning k-cycle in random graphs. Random Struct. Algorithms 53 728–751.CrossRefGoogle Scholar
Sudakov, B. and Vu, V. H. (2008) Local resilience of graphs. Random Struct. Algorithms 33 409–433.CrossRefGoogle Scholar
Tikhomirov, K. and Youssef, P. (2019) The spectral gap of dense random regular graphs. Ann. Probab. 47 362–419.Google Scholar
Wormald, N. C. (1999) Models of random regular graphs. In Surveys in Combinatorics (Canterbury, 1999), Vol. 267 of London Mathematical Society Lecture Note Series, pp. 239–298. Cambridge University Press.Google Scholar