Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-30T02:53:20.087Z Has data issue: false hasContentIssue false
  • English
  • Français

Decomposition of Multiple Packings with Subquadratic Union Complexity

Published online by Cambridge University Press:  04 January 2016

JÁNOS PACH  and
BARTOSZ WALCZAK
JÁNOS PACH
Affiliation:
École Polytechnique Fédérale de Lausanne, Switzerland and Alfred Rényi Institute of Mathematics, Hungarian Academy of Sciences, Budapest, Hungary (e-mail: [email protected])
BARTOSZ WALCZAK
Affiliation:
Theoretical Computer Science Department, Faculty of Mathematics and Computer Science, Jagiellonian University, Kraków, Poland (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose k is a positive integer and 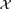${\cal X}$ is a k-fold packing of the plane by infinitely many arc-connected compact sets, which means that every point of the plane belongs to at most k sets. Suppose there is a function f(n) = o(n2) with the property that any n members of 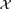${\cal X}$ determine at most f(n) holes, which means that the complement of their union has at most f(n) bounded connected components. We use tools from extremal graph theory and the topological Helly theorem to prove that 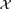${\cal X}$ can be decomposed into at most p (1-fold) packings, where p is a constant depending only on k and f.

Keywords

Primary 52C15Secondary 05B40
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 25 , Issue 1: Oberwolfach Special Issue Part 2 , January 2016 , pp. 145 - 153
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Asplund, E. and Grünbaum, B. (1960) On a colouring problem. Math. Scand. 8 181–188.CrossRefGoogle Scholar
[2]de Berg, M. (2008) Improved bounds on the union complexity of fat objects. Discrete Comput. Geom. 40 127–140.CrossRefGoogle Scholar
[3]Blundon, W. J. (1957) Multiple covering of the plane by circles. Mathematika 4 7–16.CrossRefGoogle Scholar
[4]Burling, J. P. (1965) On coloring problems of families of prototypes. PhD thesis, University of Colorado, Boulder.Google Scholar
[5]Clarkson, K. L. and Shor, P. W. (1989) Applications of random sampling in computational geometry II. Discrete Comput. Geom. 4 387–421.CrossRefGoogle Scholar
[6]Dumir, V. C. and Hans-Gill, R. J. (1972) Lattice double packings in the plane. Indian J. Pure Appl. Math. 3 481–487.Google Scholar
[7]Efrat, A. (2005) The complexity of the union of (α,β)-covered objects. SIAM J. Comput. 34 775–787.CrossRefGoogle Scholar
[8]Efrat, A., Rote, G. and Sharir, M. (1993) On the union of fat wedges and separating a collection of segments by a line. Comput. Geom. 3 277–288.CrossRefGoogle Scholar
[9]Efrat, A. and Sharir, M. (2000) On the complexity of the union of fat convex objects in the plane. Discrete Comput. Geom. 23 171–189.CrossRefGoogle Scholar
[10]Fejes, Tóth L. (1953) Lagerungen in der Ebene, auf der Kugel und im Raum (Arrangements in the plane, on the sphere, and in space), Vol. 65 of Grundlehren der Mathematischen Wissenschaft, Springer.Google Scholar
[11]FejesTóth, G. Tóth, G. and Kuperberg, W. (1993) A survey of recent results in the theory of packing and covering. In New Trends in Discrete and Computational Geometry (Pach, J., ed.), Vol. 10 of Algorithms Combin., Springer, pp. 251–279.Google Scholar
[12]Fox, J. and Pach, J. (2010) A separator theorem for string graphs and its applications. Combin. Probab. Comput. 19 371–390.CrossRefGoogle Scholar
[13]Fox, J. and Pach, J. (2014) Applications of a new separator theorem for string graphs. Combin. Probab. Comput. 23 66–74.CrossRefGoogle Scholar
[14]Helly, E. (1930) Über Systeme von abgeschlossen Mengen mit gemeinschaftlichen Punkten (On systems of closed sets with common points). Monatsh. Math. Phys. 37 281–302.CrossRefGoogle Scholar
[15]Heppes, A. (1959) Mehrfache gitterförmige Kreislagerungen in der Ebene (Multiple lattice circle packings in the plane). Acta Math. Acad. Sci. Hungar. 10 141–148.CrossRefGoogle Scholar
[16]Katona, G., Nemetz, T. and Simonovits, M. (1964) Újabb bizonyítás a Turán-féle gráftételre, és megjegyzések bizonyos általánosításaira (Another proof of Turán's graph theorem and remarks on its generalizations). Mat. Lapok 15 228–238.Google Scholar
[17]Kedem, K., RonLivne, R. Livne, R., Pach, J. and Sharir, M. (1986) On the union of Jordan regions and collision-free translational motion amidst polygonal obstacles. Discrete Comput. Geom. 1 59–71.CrossRefGoogle Scholar
[18]Kostochka, A. (2004) Coloring intersection graphs of geometric figures with a given clique number. In Towards a Theory of Geometric Graphs (Pach, J., ed.), Vol. 342 of Contemp. Math., AMS, pp. 127–138.CrossRefGoogle Scholar
[19]van Kreveld, M. (1998) On fat partitioning, fat covering, and the union size of polygons. Comput. Geom. 9 197–210.CrossRefGoogle Scholar
[20]Matoušek, J., Pach, J., Sharir, M., Sifrony, S. and Welzl, E. (1994) Fat triangles determine linearly many holes. SIAM J. Comput. 23 154–169.CrossRefGoogle Scholar
[21]Micek, P. and Pinchasi, R. Note on the number of edges in families with linear union-complexity. arXiv:1312.1678Google Scholar
[22]Pach, J. (1980) Decomposition of multiple packing and covering. In Diskrete Geometrie, Vol. 2 of Kolloq. Inst. Math. Univ. Salzburg, pp. 169–178.Google Scholar
[23]Pawlik, A., Kozik, J., Krawczyk, T., Lasoń, M., Micek, P., Trotter, W. T. and Walczak, B. (2013) Triangle-free geometric intersection graphs with large chromatic number. Discrete Comput. Geom. 50 714–726.CrossRefGoogle Scholar
[24]Pawlik, A., Kozik, J., Krawczyk, T., Lasoń, M., Micek, P., Trotter, W. T. and Walczak, B. (2014) Triangle-free intersection graphs of line segments with large chromatic number. J. Combin. Theory Ser. B 105 6–10.CrossRefGoogle Scholar
[25]Sharir, M. (1991) On k-sets in arrangements of curves and surfaces. Discrete Comput. Geom. 6 593–613.CrossRefGoogle Scholar
[26]Spencer, J. (1972) Turán's theorem for k-graphs. Discrete Math. 2 183–186.CrossRefGoogle Scholar