Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T13:42:19.114Z Has data issue: false hasContentIssue false
  • English
  • Français

Cross t-Intersecting Integer Sequences from Weighted Erdős–Ko–Rado

Published online by Cambridge University Press:  09 May 2013

NORIHIDE TOKUSHIGE
NORIHIDE TOKUSHIGE*
Affiliation:
College of Education, Ryukyu University, Nishihara, Okinawa 903-0213, Japan (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let m,n and t be positive integers. Consider [m]n as the set of sequences of length n on an m-letter alphabet. We say that two subsets A⊂[m]n and B⊂[m]n cross t-intersect if any two sequences a∈A and b∈B match in at least t positions. In this case it is shown that if 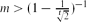$m > (1-\frac 1{\sqrt[t]2})^{-1}$ then |A||B|≤(mn−t)2. We derive this result from a weighted version of the Erdős–Ko–Rado theorem concerning cross t-intersecting families of subsets, and we also include the corresponding stability statement. One of our main tools is the eigenvalue method for intersection matrices due to Friedgut [10].

Keywords

Primary 05D05Secondary 05C50
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 22 , Issue 4 , July 2013 , pp. 622 - 637
Copyright
Copyright © Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Ahlswede, R. and Khachatrian, L. H. (1998) The diametric theorem in Hamming spaces: Optimal anticodes. Adv. Appl. Math. 20 429–449.CrossRefGoogle Scholar
[2]Bey, C. and Engel, K. (2000) Old and new results for the weighted t-intersection problem via AK-methods. In Numbers, Information and Complexity (Althofer, I.et al., eds), Kluwer, pp. 45–74.Google Scholar
[3]Dinur, I. and Safra, S. (2005) On the hardness of approximating minimum vertex cover. Ann. of Math. 162 439–485.Google Scholar
[4]Ellis, D., Friedgut, E. and Pilpel, H. (2011) Intersecting families of permutations. J. Amer. Math. Soc. 24 649–682.Google Scholar
[5]Erdős, P., Ko, C. and Rado, R. (1961) Intersection theorems for systems of finite sets. Quart. J. Math. Oxford (2) 12 313–320.Google Scholar
[6]Frankl, P. and Füredi, Z. (1980) The Erdős–Ko–Rado theorem for integer sequences. SIAM J. Alg. Discrete Math. 1 376–381.CrossRefGoogle Scholar
[7]Frankl, P., Lee, S. J., Siggers, M. and Tokushige, N. An Erdős–Ko–Rado theorem for cross t-intersecting families. arXiv:1303.0657Google Scholar
[8]Frankl, P. and Tokushige, N. (1999) The Erdős–Ko–Rado theorem for integer sequences. Combinatorica 19 55–63.CrossRefGoogle Scholar
[9]Frankl, P. and Wilson, R. M. (1986) The Erdős–Ko–Rado theorem for vector spaces. J. Combin. Theory Ser. A 43 228–236.Google Scholar
[10]Friedgut, E. (2008) On the measure of intersecting families, uniqueness and stability. Combinatorica 28 503–528.Google Scholar
[11]Gromov, M. (2010) Singularities, expanders and topology of maps 2: From combinatorics to topology via algebraic isoperimetry. Geom. Funct. Anal. 20 416–526.CrossRefGoogle Scholar
[12]Kleitman, D. J. (1966) Families of non-disjoint subsets. J. Combin. Theory 1 153–155.Google Scholar
[13]Matsumoto, M. and Tokushige, N. (1989) The exact bound in the Erdős–Ko–Rado theorem for cross-intersecting families. J. Combin. Theory Ser. A 22 90–97.Google Scholar
[14]Tokushige, N. (2005) Intersecting families: Uniform versus weighted. Ryukyu Math. J. 18 89–103.Google Scholar
[15]Tokushige, N.The eigenvalue method for cross t-intersecting families. J. Alg. Combin. DOI: 10.1007/s10801-012-0419-4.Google Scholar
[16]Wilson, R. M. (1984) The exact bound in the Erdős–Ko–Rado theorem. Combinatorica 4 247–257.Google Scholar