Published online by Cambridge University Press: 13 October 2020
A k-uniform tight cycle 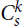 $C_s^k$ is a hypergraph on s > k vertices with a cyclic ordering such that every k consecutive vertices under this ordering form an edge. The pair (k, s) is admissible if gcd (k, s) = 1 or k / gcd (k,s) is even. We prove that if
$C_s^k$ is a hypergraph on s > k vertices with a cyclic ordering such that every k consecutive vertices under this ordering form an edge. The pair (k, s) is admissible if gcd (k, s) = 1 or k / gcd (k,s) is even. We prove that if 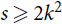 $s \ge 2{k^2}$ and H is a k-uniform hypergraph with minimum codegree at least (1/2 + o(1))|V(H)|, then every vertex is covered by a copy of
$s \ge 2{k^2}$ and H is a k-uniform hypergraph with minimum codegree at least (1/2 + o(1))|V(H)|, then every vertex is covered by a copy of 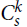 $C_s^k$. The bound is asymptotically sharp if (k, s) is admissible. Our main tool allows us to arbitrarily rearrange the order in which a tight path wraps around a complete k-partite k-uniform hypergraph, which may be of independent interest.
$C_s^k$. The bound is asymptotically sharp if (k, s) is admissible. Our main tool allows us to arbitrarily rearrange the order in which a tight path wraps around a complete k-partite k-uniform hypergraph, which may be of independent interest.
For hypergraphs F and H, a perfect F-tiling in H is a spanning collection of vertex-disjoint copies of F. For 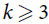 $k \ge 3$, there are currently only a handful of known F-tiling results when F is k-uniform but not k-partite. If s ≢ 0 mod k, then
$k \ge 3$, there are currently only a handful of known F-tiling results when F is k-uniform but not k-partite. If s ≢ 0 mod k, then 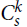 $C_s^k$ is not k-partite. Here we prove an F-tiling result for a family of non-k-partite k-uniform hypergraphs F. Namely, for
$C_s^k$ is not k-partite. Here we prove an F-tiling result for a family of non-k-partite k-uniform hypergraphs F. Namely, for 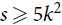 $s \ge 5{k^2}$, every k-uniform hypergraph H with minimum codegree at least (1/2 + 1/(2s) + o(1))|V(H)| has a perfect
$s \ge 5{k^2}$, every k-uniform hypergraph H with minimum codegree at least (1/2 + 1/(2s) + o(1))|V(H)| has a perfect 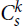 $C_s^k$-tiling. Moreover, the bound is asymptotically sharp if k is even and (k, s) is admissible.
$C_s^k$-tiling. Moreover, the bound is asymptotically sharp if k is even and (k, s) is admissible.
The research leading to these results was partially supported by FAPESP (Proc. 2013/03447-6, 2014/18641-5, 2015/07869-8) (J. Han) EPSRC, grant EP/P002420/1 (A. Lo) and the Becas Chile scholarship scheme from CONICYT (N. Sanhueza-Matamala).