Article contents
Conflict-Free Colourings of Graphs and Hypergraphs
Published online by Cambridge University Press: 01 September 2009
Abstract
A colouring of the vertices of a hypergraph H is called conflict-free if each hyperedge E of H contains a vertex of ‘unique’ colour that does not get repeated in E. The smallest number of colours required for such a colouring is called the conflict-free chromatic number of H, and is denoted by χCF(H). This parameter was first introduced by Even, Lotker, Ron and Smorodinsky (FOCS 2002) in a geometric setting, in connection with frequency assignment problems for cellular networks. Here we analyse this notion for general hypergraphs. It is shown that 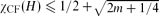 , for every hypergraph with m edges, and that this bound is tight. Better bounds of the order of m1/t log m are proved under the assumption that the size of every edge of H is at least 2t − 1, for some t ≥ 3. Using Lovász's Local Lemma, the same result holds for hypergraphs in which the size of every edge is at least 2t − 1 and every edge intersects at most m others. We give efficient polynomial-time algorithms to obtain such colourings.
, for every hypergraph with m edges, and that this bound is tight. Better bounds of the order of m1/t log m are proved under the assumption that the size of every edge of H is at least 2t − 1, for some t ≥ 3. Using Lovász's Local Lemma, the same result holds for hypergraphs in which the size of every edge is at least 2t − 1 and every edge intersects at most m others. We give efficient polynomial-time algorithms to obtain such colourings.
Our machinery can also be applied to the hypergraphs induced by the neighbourhoods of the vertices of a graph. It turns out that in this case we need far fewer colours. For example, it is shown that the vertices of any graph G with maximum degree Δ can be coloured with log2+ε Δ colours, so that the neighbourhood of every vertex contains a point of ‘unique’ colour. We give an efficient deterministic algorithm to find such a colouring, based on a randomized algorithmic version of the Lovász Local Lemma, suggested by Beck, Molloy and Reed. To achieve this, we need to (1) correct a small error in the Molloy–Reed approach, (2) restate and re-prove their result in a deterministic form.
- Type
- Paper
- Information
- Combinatorics, Probability and Computing , Volume 18 , Issue 5: New Directions in Algorithms, Combinatorics and Optimization , September 2009 , pp. 819 - 834
- Copyright
- Copyright © Cambridge University Press 2009
References
- 65
- Cited by


