Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Yogeshwaran, D.
and
Adler, Robert J.
2015.
On the topology of random complexes built over stationary point processes.
The Annals of Applied Probability,
Vol. 25,
Issue. 6,
Alishahi, Kasra
and
Zamani, Mohammadsadegh
2015.
The spherical ensemble and uniform distribution of points on the sphere.
Electronic Journal of Probability,
Vol. 20,
Issue. none,
Bradic, Jelena
2016.
Randomized maximum-contrast selection: Subagging for large-scale regression.
Electronic Journal of Statistics,
Vol. 10,
Issue. 1,
BRÄNDÉN, P.
LEANDER, M.
and
VISONTAI, M.
2016.
Multivariate Eulerian Polynomials and Exclusion Processes.
Combinatorics, Probability and Computing,
Vol. 25,
Issue. 4,
p.
486.
Yogeshwaran, D.
Subag, Eliran
and
Adler, Robert J.
2017.
Random geometric complexes in the thermodynamic regime.
Probability Theory and Related Fields,
Vol. 167,
Issue. 1-2,
p.
107.
Chambaz, Antoine
Joly, Emilien
and
Mary, Xavier
2018.
Targeted Learning in Data Science.
p.
541.
Chafaï, Djalil
Hardy, Adrien
and
Maïda, Mylène
2018.
Concentration for Coulomb gases and Coulomb transport inequalities.
Journal of Functional Analysis,
Vol. 275,
Issue. 6,
p.
1447.
Rose, Sherri
and
van der Laan, Mark J.
2018.
Targeted Learning in Data Science.
p.
3.
Balzer, Laura B.
van der Laan, Mark J.
and
Petersen, Maya L.
2018.
Targeted Learning in Data Science.
p.
195.
Kyng, Rasmus
and
Song, Zhao
2018.
A Matrix Chernoff Bound for Strongly Rayleigh Distributions and Spectral Sparsifiers from a few Random Spanning Trees.
p.
373.
Carroll, Tom
Marzo, Jordi
Massaneda, Xavier
and
Ortega-Cerdà, Joaquim
2018.
Equidistribution and β-ensembles.
Annales de la Faculté des sciences de Toulouse : Mathématiques,
Vol. 27,
Issue. 2,
p.
377.
Coeurjolly, Jean-François
and
Reynaud-Bouret, Patricia
2019.
A concentration inequality for inhomogeneous Neyman–Scott point processes.
Statistics & Probability Letters,
Vol. 148,
Issue. ,
p.
30.
Loonis, V.
and
Mary, X.
2019.
Determinantal sampling designs.
Journal of Statistical Planning and Inference,
Vol. 199,
Issue. ,
p.
60.
Cryan, Mary
Guo, Heng
and
Mousa, Giorgos
2019.
Modified log-Sobolev Inequalities for Strongly Log-Concave Distributions.
p.
1358.
Ben-Hamou, Anna
2020.
A threshold for cutoff in two-community random graphs.
The Annals of Applied Probability,
Vol. 30,
Issue. 4,
Aoun, Richard
Banna, Marwa
and
Youssef, Pierre
2020.
Matrix Poincaré inequalities and concentration.
Advances in Mathematics,
Vol. 371,
Issue. ,
p.
107251.
Andreas Klatt, Michael
Last, Günter
and
Yogeshwaran, D.
2020.
Hyperuniform and rigid stable matchings.
Random Structures & Algorithms,
Vol. 57,
Issue. 2,
p.
439.
Anari, Nima
and
Derezinski, Michal
2020.
Isotropy and Log-Concave Polynomials: Accelerated Sampling and High-Precision Counting of Matroid Bases.
p.
1331.
Cryan, Mary
Guo, Heng
and
Mousa, Giorgos
2021.
Modified log-Sobolev inequalities for strongly log-concave distributions.
The Annals of Probability,
Vol. 49,
Issue. 1,
Fanuel, Michael
Schreurs, Joachim
and
Suykens, Johan
2021.
Diversity Sampling is an Implicit Regularization for Kernel Methods.
SIAM Journal on Mathematics of Data Science,
Vol. 3,
Issue. 1,
p.
280.
 $\mathbb{R}$ be a Lipschitz function. Under a negative dependence hypothesis known as the strong Rayleigh condition, we show that f −
$\mathbb{R}$ be a Lipschitz function. Under a negative dependence hypothesis known as the strong Rayleigh condition, we show that f −  ${\mathbb E}$f satisfies a concentration inequality. The class of strong Rayleigh measures includes determinantal measures, weighted uniform matroids and exclusion measures; some familiar examples from these classes are generalized negative binomials and spanning tree measures. For instance, any Lipschitz-1 function of the edges of a uniform spanning tree on vertex set V (e.g., the number of leaves) satisfies the Gaussian concentration inequality
${\mathbb E}$f satisfies a concentration inequality. The class of strong Rayleigh measures includes determinantal measures, weighted uniform matroids and exclusion measures; some familiar examples from these classes are generalized negative binomials and spanning tree measures. For instance, any Lipschitz-1 function of the edges of a uniform spanning tree on vertex set V (e.g., the number of leaves) satisfies the Gaussian concentration inequality
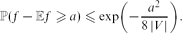 \begin{linenomath}$${{\mathbb P} (f - {\mathbb E} f \geq a) \leq \exp \biggl( - \frac{a^2}{8 \, |V|} \biggr) }.$$\end{linenomath}
\begin{linenomath}$${{\mathbb P} (f - {\mathbb E} f \geq a) \leq \exp \biggl( - \frac{a^2}{8 \, |V|} \biggr) }.$$\end{linenomath}

