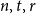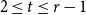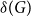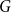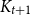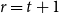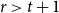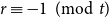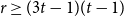1. Introduction
The foundation stone of extremal graph theory is Turán’s theorem from 1941 [Reference Turán14], which states that the Turán graph
![]() $T_t(n)$
(the complete
$T_t(n)$
(the complete
![]() $t$
-partite graph on
$t$
-partite graph on
![]() $n$
vertices with parts of size
$n$
vertices with parts of size
![]() $\left \lceil \frac{n}{t}\right \rceil$
or
$\left \lceil \frac{n}{t}\right \rceil$
or
![]() $\left \lfloor \frac{n}{t}\right \rfloor$
) has the most edges among all
$\left \lfloor \frac{n}{t}\right \rfloor$
) has the most edges among all
![]() $K_{t+1}$
-free graphs on
$K_{t+1}$
-free graphs on
![]() $n$
vertices. Erdős [Reference Erdős7] and Bollobás, Erdős, and Szemerédi [Reference Bollobás, Erdős and Szemerédi5] asked the following Turán-type problem for multipartite graphs.
$n$
vertices. Erdős [Reference Erdős7] and Bollobás, Erdős, and Szemerédi [Reference Bollobás, Erdős and Szemerédi5] asked the following Turán-type problem for multipartite graphs.
Problem 1.1. Given integers
![]() $n$
and
$n$
and
![]() $2\le t\le r-1$
, what is the largest minimum degree
$2\le t\le r-1$
, what is the largest minimum degree
![]() $\delta (G)$
among all
$\delta (G)$
among all
![]() $r$
-partite graphs
$r$
-partite graphs
![]() $G$
with parts of size
$G$
with parts of size
![]() $n$
and which do not contain a copy of
$n$
and which do not contain a copy of
![]() $K_{t+1}$
?
$K_{t+1}$
?
Let
![]() $f(n, r, t+1)$
denote the answer to Problem 1.1. At a meeting in 1972, Erdős conjectured that
$f(n, r, t+1)$
denote the answer to Problem 1.1. At a meeting in 1972, Erdős conjectured that
![]() $f(n, r, r)= (r-2)n$
, see [Reference Erdős7, Problem 2, 353–354]. Graver gave a short and elegant proof for
$f(n, r, r)= (r-2)n$
, see [Reference Erdős7, Problem 2, 353–354]. Graver gave a short and elegant proof for
![]() $r=3$
but Seymour constructed counterexamples for
$r=3$
but Seymour constructed counterexamples for
![]() $r\ge 4$
, see [Reference Bollobás, Erdős and Szemerédi5]. The study of
$r\ge 4$
, see [Reference Bollobás, Erdős and Szemerédi5]. The study of
![]() $f(n, r, r)$
(mostly in its complementary form concerning independent transversals) has been a central topic in Combinatorics (see, e.g., [Reference Alon1, Reference Haxell and Szabó9–Reference Jin11, Reference Szabó and Tardos13]) due to its applications in graph arboricity, list colouring, and strong chromatic numbers. The problem of determining
$f(n, r, r)$
(mostly in its complementary form concerning independent transversals) has been a central topic in Combinatorics (see, e.g., [Reference Alon1, Reference Haxell and Szabó9–Reference Jin11, Reference Szabó and Tardos13]) due to its applications in graph arboricity, list colouring, and strong chromatic numbers. The problem of determining
![]() $f(n, r, r)$
was finally settled by Haxell and Szabó [Reference Haxell and Szabó9] and Szabó and Tardos [Reference Szabó and Tardos13]; indeed, for every
$f(n, r, r)$
was finally settled by Haxell and Szabó [Reference Haxell and Szabó9] and Szabó and Tardos [Reference Szabó and Tardos13]; indeed, for every
![]() $n\in \mathbb{N}$
and even
$n\in \mathbb{N}$
and even
![]() $r\ge 2$
,
$r\ge 2$
,
In contrast, little is known about the value of
![]() $f(n, r, t+1)$
for
$f(n, r, t+1)$
for
![]() $r\gt t+1$
. In 1975 Bollobás, Erdős, and Szemerédi [Reference Bollobás, Erdős and Szemerédi5] stated Problem 1.1 explicitly and noted that Turán’s theorem easily implies that
$r\gt t+1$
. In 1975 Bollobás, Erdős, and Szemerédi [Reference Bollobás, Erdős and Szemerédi5] stated Problem 1.1 explicitly and noted that Turán’s theorem easily implies that
Indeed, for any
![]() $r\ge t+1$
, Turán’s theorem implies that every
$r\ge t+1$
, Turán’s theorem implies that every
![]() $K_{t+1}$
-free graph
$K_{t+1}$
-free graph
![]() $G$
on
$G$
on
![]() $rn$
vertices has at most
$rn$
vertices has at most
![]() $(1- 1/t)(rn)^2/2$
edges, and thus
$(1- 1/t)(rn)^2/2$
edges, and thus
![]() $\delta (G)\le (1- 1/t)rn$
. On the other hand, we may let
$\delta (G)\le (1- 1/t)rn$
. On the other hand, we may let
![]() $G$
be the complete
$G$
be the complete
![]() $t$
-partite graph on
$t$
-partite graph on
![]() $r n$
vertices with parts of size
$r n$
vertices with parts of size
![]() $\left \lceil \frac{r}{t}\right \rceil n$
or
$\left \lceil \frac{r}{t}\right \rceil n$
or
![]() $\left \lfloor \frac{r}{t}\right \rfloor n$
(in other words,
$\left \lfloor \frac{r}{t}\right \rfloor n$
(in other words,
![]() $G$
is an
$G$
is an
![]() $n$
-vertex blow-up of the Turán graph
$n$
-vertex blow-up of the Turán graph
![]() $T_{t}(r)$
). Then
$T_{t}(r)$
). Then
Extending Graver’s work on
![]() $f(n, 3, 3)$
, Bollobás, Erdős, and Straus [Reference Bollobás, Erdős and Straus4] answered Problem 1.1 for all (not necessarily balanced)
$f(n, 3, 3)$
, Bollobás, Erdős, and Straus [Reference Bollobás, Erdős and Straus4] answered Problem 1.1 for all (not necessarily balanced)
![]() $r$
-partite graphs
$r$
-partite graphs
![]() $G$
when
$G$
when
![]() $t=2$
. Their result implies that for every
$t=2$
. Their result implies that for every
![]() $n\in \mathbb{N}$
and
$n\in \mathbb{N}$
and
![]() $r \geq 3$
,
$r \geq 3$
,
The aim of this article is to rebuild momentum on Problem 1.1 for
![]() $r\gt t+1\geq 4$
. For any such choice of
$r\gt t+1\geq 4$
. For any such choice of
![]() $r$
and
$r$
and
![]() $t$
, our results either resolve Problem 1.1 or provide a lower bound on
$t$
, our results either resolve Problem 1.1 or provide a lower bound on
![]() $f(n,r,t+1)$
that improves that given in (1.3). In particular, in the case that
$f(n,r,t+1)$
that improves that given in (1.3). In particular, in the case that
![]() $r \equiv -1 \pmod{t}$
, our first result shows that the lower bound in (1.3) is tight.
$r \equiv -1 \pmod{t}$
, our first result shows that the lower bound in (1.3) is tight.
Theorem 1.2.
Given integers
![]() $n\ge 1$
,
$n\ge 1$
,
![]() $m\ge 2$
, and
$m\ge 2$
, and
![]() $t \ge 3$
, let
$t \ge 3$
, let
![]() $r=mt-1$
. Then
$r=mt-1$
. Then
![]() $f(n, r, t+1) =\left ( r - \left \lceil{r}/{t}\right \rceil \right ) n$
.
$f(n, r, t+1) =\left ( r - \left \lceil{r}/{t}\right \rceil \right ) n$
.
It turns out that the lower bound in (1.3) is best possible only if
![]() $r \equiv 0,-1 \pmod{t}$
; in all other cases we give constructions that improve on this lower bound (see Section 4). Moreover, in many such cases, including when
$r \equiv 0,-1 \pmod{t}$
; in all other cases we give constructions that improve on this lower bound (see Section 4). Moreover, in many such cases, including when
![]() $r \ge (3t-1)(t-1)$
, we determine
$r \ge (3t-1)(t-1)$
, we determine
![]() $f(n,r,t+1)$
up to an additive constant.
$f(n,r,t+1)$
up to an additive constant.
Theorem 1.3.
Given integers
![]() $n\ge 1, m\ge 2, t \ge 3$
, let
$n\ge 1, m\ge 2, t \ge 3$
, let
![]() $r = mt -a$
with
$r = mt -a$
with
![]() $2 \le a \le \min \{m, t-1\}$
. Suppose
$2 \le a \le \min \{m, t-1\}$
. Suppose
-
(i)
 $r \ge a(3t-1)$
or
$r \ge a(3t-1)$
or
-
(ii)
 $\dfrac{r}{t(3t-1)(m-1)}-\dfrac{a}{t(m-1)} + \dfrac{a-1}{mt-2} \geq \dfrac{1}{n}$
.
$\dfrac{r}{t(3t-1)(m-1)}-\dfrac{a}{t(m-1)} + \dfrac{a-1}{mt-2} \geq \dfrac{1}{n}$
.
Then
Thus, up to an additive constant, (1.2), Theorems 1.2 and 1.3 together resolve Problem 1.1 whenever
![]() $r \geq (3t-1)(t-1)$
. In particular, if
$r \geq (3t-1)(t-1)$
. In particular, if
![]() $r \geq (3t-1)(t-1)$
,
$r \geq (3t-1)(t-1)$
,
![]() $r \not \equiv 0 \pmod{t}$
, and
$r \not \equiv 0 \pmod{t}$
, and
![]() $\lceil r/t \rceil t-2$
divides
$\lceil r/t \rceil t-2$
divides
![]() $n$
, then
$n$
, then
Combining the last two theorems with (1.2), we essentially determine
![]() $f(n,r,4)$
for all
$f(n,r,4)$
for all
![]() $r \not = 7$
.
$r \not = 7$
.
Corollary 1.4.
Let
![]() $r \ge 5$
with
$r \ge 5$
with
![]() $r \ne 7$
. Suppose
$r \ne 7$
. Suppose
![]() $n \geq 60$
if
$n \geq 60$
if
![]() $r=10$
;
$r=10$
;
![]() $ n \geq 22$
if
$ n \geq 22$
if
![]() $r=13$
, and
$r=13$
, and
![]() $n\in \mathbb N$
otherwise. Then
$n\in \mathbb N$
otherwise. Then
 \begin{align*} f(n,r,4) = \begin{cases} \left (r- \lfloor r/3 \rfloor \right )\frac{r-1}{r} n - c_r & \text{ if } r \equiv 1 \pmod{3},\\[4pt] \left ( r - \left \lceil{r}/{3}\right \rceil \right ) n &\text{otherwise}, \end{cases} \end{align*}
\begin{align*} f(n,r,4) = \begin{cases} \left (r- \lfloor r/3 \rfloor \right )\frac{r-1}{r} n - c_r & \text{ if } r \equiv 1 \pmod{3},\\[4pt] \left ( r - \left \lceil{r}/{3}\right \rceil \right ) n &\text{otherwise}, \end{cases} \end{align*}
where
![]() $0 \le c_r \le r/3$
.
$0 \le c_r \le r/3$
.
The proof of Theorem 1.3 applies a result of Andrásfai, Erdős, and Sós [Reference Andrásfai, Erdős and Sós2]. In particular, this result allows us conclude that, if
![]() $r$
is large compared to
$r$
is large compared to
![]() $t$
, then
$t$
, then
![]() $f(n,r,t+1)$
is equal to the maximum of the minimum degrees among the family of balanced
$f(n,r,t+1)$
is equal to the maximum of the minimum degrees among the family of balanced
![]() $r$
-partite
$r$
-partite
![]() $rn$
-vertex graphs of chromatic number at most
$rn$
-vertex graphs of chromatic number at most
![]() $t$
. This approach is also utilized in the proof of Theorem 1.2 when
$t$
. This approach is also utilized in the proof of Theorem 1.2 when
![]() $m \geq 3$
. Interestingly, this approach breaks down when
$m \geq 3$
. Interestingly, this approach breaks down when
![]() $m =2$
, so we require a separate direct argument in this case (which hinges on the fact that
$m =2$
, so we require a separate direct argument in this case (which hinges on the fact that
![]() $r=2t-1$
).
$r=2t-1$
).
There are two extremal problems closely related to Problem 1.1. First, a multipartite Turán theorem has been known since the 1970s. Bollobás, Erdős, and Szemerédi [Reference Bollobás, Erdős and Szemerédi5] showed that the
![]() $n$
-vertex blow-up of
$n$
-vertex blow-up of
![]() $T_t(r)$
has the most edges among all
$T_t(r)$
has the most edges among all
![]() $r$
-partite
$r$
-partite
![]() $K_{t+1}$
-free graphs with
$K_{t+1}$
-free graphs with
![]() $n$
vertices in each part. In fact, this easily follows from Turán’s theorem and indicates that for multipartite graphs, the minimum degree version, Problem 1.1, is indeed harder than the Turán problem.Footnote
1
Furthermore, Bollobás, Erdős, and Straus [Reference Bollobás, Erdős and Straus4] determined the largest size of (not necessarily balanced)
$n$
vertices in each part. In fact, this easily follows from Turán’s theorem and indicates that for multipartite graphs, the minimum degree version, Problem 1.1, is indeed harder than the Turán problem.Footnote
1
Furthermore, Bollobás, Erdős, and Straus [Reference Bollobás, Erdős and Straus4] determined the largest size of (not necessarily balanced)
![]() $r$
-partite
$r$
-partite
![]() $K_{t+1}$
-free graphs. Another related problem concerns finding the smallest
$K_{t+1}$
-free graphs. Another related problem concerns finding the smallest
![]() $d_{r}^{t}$
such that every
$d_{r}^{t}$
such that every
![]() $r$
-partite graph whose parts have pairwise edge density greater than
$r$
-partite graph whose parts have pairwise edge density greater than
![]() $d_{r}^{ t}$
contains a copy of
$d_{r}^{ t}$
contains a copy of
![]() $K_{t}$
. Bondy, Shen, Thomassé, and Thomassen [Reference Bondy, Shen, Thomassé and Thomassen6] showed that
$K_{t}$
. Bondy, Shen, Thomassé, and Thomassen [Reference Bondy, Shen, Thomassé and Thomassen6] showed that
![]() $d_{3}^{3}=0.618\ldots$
, the golden ratio. Pfender [Reference Pfender12] showed that
$d_{3}^{3}=0.618\ldots$
, the golden ratio. Pfender [Reference Pfender12] showed that
![]() $d_r^t= (t-2)/(t-1)$
for sufficiently large
$d_r^t= (t-2)/(t-1)$
for sufficiently large
![]() $r$
; in particular,
$r$
; in particular,
![]() $d_r^3= 1/2$
for
$d_r^3= 1/2$
for
![]() $r\ge 13$
.
$r\ge 13$
.
1.1 Notation
Given a graph
![]() $G$
and
$G$
and
![]() $x \in V(G)$
, we write
$x \in V(G)$
, we write
![]() $N(x)$
for the neighbourhood of
$N(x)$
for the neighbourhood of
![]() $x$
in
$x$
in
![]() $G$
and define
$G$
and define
![]() $d (x)\,:\!=\,|N(x)|$
as the degree of
$d (x)\,:\!=\,|N(x)|$
as the degree of
![]() $x$
in
$x$
in
![]() $G$
. If
$G$
. If
![]() $X \subseteq V(G)$
we write
$X \subseteq V(G)$
we write
![]() $N(x,X)\,:\!=\,N(x)\cap X$
and
$N(x,X)\,:\!=\,N(x)\cap X$
and
![]() $d (x,X) \,:\!=\,|N(x,X)|$
. We write
$d (x,X) \,:\!=\,|N(x,X)|$
. We write
![]() $G[X]$
for the induced subgraph of
$G[X]$
for the induced subgraph of
![]() $G$
with vertex set
$G$
with vertex set
![]() $X$
.
$X$
.
Let
![]() $G$
be an
$G$
be an
![]() $r$
-partite graph with parts
$r$
-partite graph with parts
![]() $V_1,\ldots, V_r$
. A transversal is a subset
$V_1,\ldots, V_r$
. A transversal is a subset
![]() $S\subset V(G)$
so that
$S\subset V(G)$
so that
![]() $|S\cap V_i|=1$
for each part
$|S\cap V_i|=1$
for each part
![]() $V_i$
of
$V_i$
of
![]() $G$
. A set
$G$
. A set
![]() $S\subset V(G)$
is crossing if
$S\subset V(G)$
is crossing if
![]() $|S\cap V_i|\le 1$
for each part
$|S\cap V_i|\le 1$
for each part
![]() $V_i$
of
$V_i$
of
![]() $G$
. Thus, an independent transversal is simply a crossing independent set of size
$G$
. Thus, an independent transversal is simply a crossing independent set of size
![]() $r$
. Define
$r$
. Define
![]() $K_r(n)$
to be the complete
$K_r(n)$
to be the complete
![]() $r$
-partite graph where each part has size
$r$
-partite graph where each part has size
![]() $n$
.
$n$
.
1.2 Organization of paper
In Section 2, we formally restate Problem 1.1 in its complementary form and prove Theorem 1.2 for
![]() $m=2$
. In Section 3, we introduce a related parameter
$m=2$
. In Section 3, we introduce a related parameter
![]() $\delta (n,r,t)$
that is equal to
$\delta (n,r,t)$
that is equal to
![]() $f(n,r,t+1)$
if
$f(n,r,t+1)$
if
![]() $r$
is large compared to
$r$
is large compared to
![]() $t$
. In Section 4, we give constructions that improve on the lower bound in (1.3) whenever
$t$
. In Section 4, we give constructions that improve on the lower bound in (1.3) whenever
![]() $r \not \equiv 0,-1 \pmod{t}$
. We give an upper bound on
$r \not \equiv 0,-1 \pmod{t}$
. We give an upper bound on
![]() $\delta (n,r,t)$
in Section 5 that allows us to easily deduce Theorems 1.2 and 1.3 in Section 6. We finish the paper with concluding remarks in Section 7.
$\delta (n,r,t)$
in Section 5 that allows us to easily deduce Theorems 1.2 and 1.3 in Section 6. We finish the paper with concluding remarks in Section 7.
2. The complementary problem and Proof of Theorem 1.2 for
 $m=2$
$m=2$
In most papers on
![]() $f(n, r, r)$
, the complementary form of
$f(n, r, r)$
, the complementary form of
![]() $f(n, r, r)$
was considered, namely, the smallest
$f(n, r, r)$
was considered, namely, the smallest
![]() $\Delta (G)$
among all
$\Delta (G)$
among all
![]() $r$
-partite graphs
$r$
-partite graphs
![]() $G$
with parts
$G$
with parts
![]() $V_1,\ldots, V_r$
of size
$V_1,\ldots, V_r$
of size
![]() $n$
and without an independent transversal. For a couple of our proofs, it will also be easier to work in the corresponding complementary setting also.
$n$
and without an independent transversal. For a couple of our proofs, it will also be easier to work in the corresponding complementary setting also.
Let
![]() $\Delta (n, r, t) \,:\!=\, (r-1)n - f(n, r, t)$
denote the smallest maximum degree
$\Delta (n, r, t) \,:\!=\, (r-1)n - f(n, r, t)$
denote the smallest maximum degree
![]() $\Delta (G)$
among all
$\Delta (G)$
among all
![]() $r$
-partite graphs
$r$
-partite graphs
![]() $G$
with parts
$G$
with parts
![]() $V_1,\ldots, V_r$
of size
$V_1,\ldots, V_r$
of size
![]() $n$
and without a crossing independent set of size
$n$
and without a crossing independent set of size
![]() $t$
. Note that (1.3) is equivalent to
$t$
. Note that (1.3) is equivalent to
We now prove the following lemma, which is the
![]() $m=2$
case of Theorem 1.2.
$m=2$
case of Theorem 1.2.
Lemma 2.1.
For every
![]() $n\in \mathbb{N}$
and
$n\in \mathbb{N}$
and
![]() $t \ge 3$
,
$t \ge 3$
,
![]() $f(n,2t-1,t+1) = (2t-3)n$
.
$f(n,2t-1,t+1) = (2t-3)n$
.
Proof. Let
![]() $r \,:\!=\, 2t-1$
. By (1.3), it suffices to prove that
$r \,:\!=\, 2t-1$
. By (1.3), it suffices to prove that
![]() $f(n,2t-1,t+1) \le (2t-3)n$
. Further, by considering the complementary problem, it suffices to prove that if
$f(n,2t-1,t+1) \le (2t-3)n$
. Further, by considering the complementary problem, it suffices to prove that if
![]() $G$
is an
$G$
is an
![]() $r$
-partite graph with vertex classes
$r$
-partite graph with vertex classes
![]() $V_1, \ldots, V_r$
of size
$V_1, \ldots, V_r$
of size
![]() $n$
so that
$n$
so that
![]() $G$
does not contain a crossing independent set of size
$G$
does not contain a crossing independent set of size
![]() $t+1$
, then
$t+1$
, then
![]() $\Delta (G) \ge n$
.
$\Delta (G) \ge n$
.
Suppose for a contradiction that
![]() $\Delta (G) \lt n$
.
$\Delta (G) \lt n$
.
Claim 2.2.
For all
![]() $x \in V(G)$
and
$x \in V(G)$
and
![]() $i \in [r]$
, we have
$i \in [r]$
, we have
![]() $d(x,V_i) \lt n/(t-1)$
.
$d(x,V_i) \lt n/(t-1)$
.
Proof of claim. Suppose the claim is false. Let
![]() $D\,:\!=\,\max \{ d(v,V_i) \colon v \in V(G), i \in [r]\}\geq n/(t-1)$
. Without loss of generality, we may assume that there exists
$D\,:\!=\,\max \{ d(v,V_i) \colon v \in V(G), i \in [r]\}\geq n/(t-1)$
. Without loss of generality, we may assume that there exists
![]() $x_1 \in V_1$
such that
$x_1 \in V_1$
such that
![]() $d(x_1,V_2) =D$
. Since
$d(x_1,V_2) =D$
. Since
![]() $\Delta (G) \lt n$
, there exists
$\Delta (G) \lt n$
, there exists
![]() $x_2 \in V_2 \setminus N(x_1)$
. Furthermore, since
$x_2 \in V_2 \setminus N(x_1)$
. Furthermore, since
![]() $\Delta (G) \lt n$
and
$\Delta (G) \lt n$
and
![]() $r =2t-1$
, we can greedily find
$r =2t-1$
, we can greedily find
![]() $x_3, \ldots, x_{t-1}$
such that
$x_3, \ldots, x_{t-1}$
such that
![]() $S = \{x_1,\ldots, x_{t-1}\}$
is a crossing independent set.Footnote
2
Without loss of generality, assume that
$S = \{x_1,\ldots, x_{t-1}\}$
is a crossing independent set.Footnote
2
Without loss of generality, assume that
![]() $x_i \in V_i$
for
$x_i \in V_i$
for
![]() $i \in [t-1]$
.
$i \in [t-1]$
.
For each
![]() $i\in [ t]$
, let
$i\in [ t]$
, let
![]() $W_i$
consist of all the vertices of
$W_i$
consist of all the vertices of
![]() $V_{r+1-i}$
that are not adjacent to any vertex in
$V_{r+1-i}$
that are not adjacent to any vertex in
![]() $S$
. Set
$S$
. Set
![]() $n_i \,:\!=\, |W_i|$
and without loss of generality, assume that
$n_i \,:\!=\, |W_i|$
and without loss of generality, assume that
![]() $n_1 \ge n_2 \ge \ldots \ge n_{t}$
. Let
$n_1 \ge n_2 \ge \ldots \ge n_{t}$
. Let
![]() $\ell \,:\!=\, \max \{ i \in [t] \colon n_i \gt 0 \}$
. Note that
$\ell \,:\!=\, \max \{ i \in [t] \colon n_i \gt 0 \}$
. Note that
 \begin{align*} n_1+ \ldots + n_{\ell } & = n_1 + \ldots +n_{t} = \left | \bigcup _{t \le i \le r} V_{i} \setminus \bigcup _{j \in [t-1]}N(x_j) \right | \\ & \ge tn - ((t-1)\Delta (G)-d(x_1,V_2)) \gt n+D . \end{align*}
\begin{align*} n_1+ \ldots + n_{\ell } & = n_1 + \ldots +n_{t} = \left | \bigcup _{t \le i \le r} V_{i} \setminus \bigcup _{j \in [t-1]}N(x_j) \right | \\ & \ge tn - ((t-1)\Delta (G)-d(x_1,V_2)) \gt n+D . \end{align*}
By averaging, we have
Notice that the
![]() $\ell$
-partite subgraph of
$\ell$
-partite subgraph of
![]() $G$
induced by
$G$
induced by
![]() $W_1,\ldots, W_{\ell }$
must be complete (otherwise one can extend
$W_1,\ldots, W_{\ell }$
must be complete (otherwise one can extend
![]() $S$
into a crossing independent set of size
$S$
into a crossing independent set of size
![]() $t+1$
, a contradiction). Hence, there exists
$t+1$
, a contradiction). Hence, there exists
![]() $y \in W_{\ell }$
such that
$y \in W_{\ell }$
such that
![]() $\bigcup _{i \in [\ell -1]} W_i \subseteq N(y)$
. By the definition of
$\bigcup _{i \in [\ell -1]} W_i \subseteq N(y)$
. By the definition of
![]() $D$
, we deduce that
$D$
, we deduce that
Together with (2.1), this implies that
![]() $D \gt n/(\ell -1)$
and so
$D \gt n/(\ell -1)$
and so
a contradiction.
Given a crossing independent set
![]() $S$
of
$S$
of
![]() $G$
, let
$G$
, let
![]() $\sigma (S) \,:\!=\, \sum _{x \in S} d(x,V_S)$
where
$\sigma (S) \,:\!=\, \sum _{x \in S} d(x,V_S)$
where
![]() $V_S$
is the union of all
$V_S$
is the union of all
![]() $V_i$
that contain a vertex from
$V_i$
that contain a vertex from
![]() $S$
. As mentioned in Footnote 2, we can greedily construct a crossing independent set of size
$S$
. As mentioned in Footnote 2, we can greedily construct a crossing independent set of size
![]() $t$
. Let
$t$
. Let
![]() $S$
be a crossing independent set of size
$S$
be a crossing independent set of size
![]() $t$
with
$t$
with
![]() $\sigma (S)$
maximal. Without loss of generality,
$\sigma (S)$
maximal. Without loss of generality,
![]() $S \cap \bigcup _{i \in [t-1]} V_i= \emptyset$
.
$S \cap \bigcup _{i \in [t-1]} V_i= \emptyset$
.
Consider any
![]() $(t-1)$
-set
$(t-1)$
-set
![]() $S^{\prime}\subset S$
. By Claim 2.2, there exists a vertex
$S^{\prime}\subset S$
. By Claim 2.2, there exists a vertex
![]() $y \in V_1$
that is not adjacent to any vertex in
$y \in V_1$
that is not adjacent to any vertex in
![]() $S^{\prime}$
. Note that
$S^{\prime}$
. Note that
![]() $S^{\prime}\cup \{y\}$
is a crossing independent set of size
$S^{\prime}\cup \{y\}$
is a crossing independent set of size
![]() $t$
. Hence,
$t$
. Hence,
![]() $ \sigma (S) \ge \sigma (S^{\prime}\cup \{y\} ) \ge \sigma (S^{\prime}) + \sum _{x\in S^{\prime}} d(x,V_1)$
. By summing over all
$ \sigma (S) \ge \sigma (S^{\prime}\cup \{y\} ) \ge \sigma (S^{\prime}) + \sum _{x\in S^{\prime}} d(x,V_1)$
. By summing over all
![]() $(t-1)$
-sets
$(t-1)$
-sets
![]() $S^{\prime}\subset S$
, we obtain that
$S^{\prime}\subset S$
, we obtain that
 \begin{align*} t \sigma (S) & \ge \sum _{S^{\prime} \subset S \colon |S^{\prime}|=t-1} \sigma (S^{\prime}) + (t-1) \sum _{x \in S}d(x,V_1) = (t-2)\sigma (S) + (t-1) \sum _{x \in S}d(x,V_1)\\ & \ge (t-2)\sigma (S) + (t-1)n, \end{align*}
\begin{align*} t \sigma (S) & \ge \sum _{S^{\prime} \subset S \colon |S^{\prime}|=t-1} \sigma (S^{\prime}) + (t-1) \sum _{x \in S}d(x,V_1) = (t-2)\sigma (S) + (t-1) \sum _{x \in S}d(x,V_1)\\ & \ge (t-2)\sigma (S) + (t-1)n, \end{align*}
where the last inequality follows as every vertex in
![]() $V_1$
must be adjacent to at least one vertex in
$V_1$
must be adjacent to at least one vertex in
![]() $S$
(else there exists a crossing independent set of size
$S$
(else there exists a crossing independent set of size
![]() $t+1$
, a contradiction). Thus,
$t+1$
, a contradiction). Thus,
![]() $ \sigma (S) \ge (t-1) n/2$
.
$ \sigma (S) \ge (t-1) n/2$
.
As
![]() $S \cap \bigcup _{i \in [t-1]} V_i= \emptyset$
, then
$S \cap \bigcup _{i \in [t-1]} V_i= \emptyset$
, then
![]() $\bigcup _{i \in [t-1]} V_i \subseteq \bigcup _{x \in S} N(x)$
or else there exists a crossing independent set of size
$\bigcup _{i \in [t-1]} V_i \subseteq \bigcup _{x \in S} N(x)$
or else there exists a crossing independent set of size
![]() $t+1$
, a contradiction. Therefore,
$t+1$
, a contradiction. Therefore,
 \begin{align*} t \Delta (G) \ge \sum _{x \in S} d(x) \ge \sigma (S) + \left |\bigcup _{i \in [t-1]} V_i \right | \ge \frac{(t-1)n}2 + (t-1) n \ge t n, \end{align*}
\begin{align*} t \Delta (G) \ge \sum _{x \in S} d(x) \ge \sigma (S) + \left |\bigcup _{i \in [t-1]} V_i \right | \ge \frac{(t-1)n}2 + (t-1) n \ge t n, \end{align*}
implying that
![]() $\Delta (G) \ge n$
, a contradiction.
$\Delta (G) \ge n$
, a contradiction.
3. A connection to the parameter
 $\delta (n,r,t)$
$\delta (n,r,t)$
The following problem turns out to be closely related to Problem 1.1. Let
![]() $\mathcal{G}(n,r,t)$
be the family of all
$\mathcal{G}(n,r,t)$
be the family of all
![]() $r$
-partite graphs
$r$
-partite graphs
![]() $G$
with parts of size
$G$
with parts of size
![]() $n$
and with chromatic number
$n$
and with chromatic number
![]() $\chi (G) \le t$
. Let
$\chi (G) \le t$
. Let
![]() $\delta (n,r,t) \,:\!=\, \max \{ \delta (G) \colon G \in \mathcal{G}(n,r,t)\}$
. An
$\delta (n,r,t) \,:\!=\, \max \{ \delta (G) \colon G \in \mathcal{G}(n,r,t)\}$
. An
![]() $n$
-vertex blow-up of the Turán graph
$n$
-vertex blow-up of the Turán graph
![]() $T_{t}(r)$
is a member of
$T_{t}(r)$
is a member of
![]() $\mathcal{G}(n,r,t)$
. Together with (1.3), this gives
$\mathcal{G}(n,r,t)$
. Together with (1.3), this gives
Therefore, when
![]() $t$
divides
$t$
divides
![]() $r$
, we have
$r$
, we have
![]() $\delta (n,r,t) = f(n, r, t+1) = (r - r/t)n$
.
$\delta (n,r,t) = f(n, r, t+1) = (r - r/t)n$
.
When
![]() $r$
is large compared to
$r$
is large compared to
![]() $t$
, Corollary 3.3 below implies that
$t$
, Corollary 3.3 below implies that
![]() $f(n,r,t+1) = \delta (n,r,t)$
as well. In fact, this is an easy consequence of the following result of Andrásfai, Erdős, and Sós [Reference Andrásfai, Erdős and Sós2].
$f(n,r,t+1) = \delta (n,r,t)$
as well. In fact, this is an easy consequence of the following result of Andrásfai, Erdős, and Sós [Reference Andrásfai, Erdős and Sós2].
Theorem 3.1. (Andrásfai, Erdős, and Sós [Reference Andrásfai, Erdős and Sós2].) Let
![]() $t \ge 2$
and let
$t \ge 2$
and let
![]() $G$
be a
$G$
be a
![]() $K_{t+1}$
-free graph on
$K_{t+1}$
-free graph on
![]() $N$
vertices. If
$N$
vertices. If
![]() $\delta (G) \gt \frac{3t-4}{3t-1} N$
, then
$\delta (G) \gt \frac{3t-4}{3t-1} N$
, then
![]() $\chi (G) \le t$
.
$\chi (G) \le t$
.
Corollary 3.2.
For
![]() $r \gt t \ge 2$
,
$r \gt t \ge 2$
,
![]() $f(n,r,t+1) \le \max \left \{ \frac{3t-4}{3t-1} (rn), \delta (n,r,t) \right \}$
.
$f(n,r,t+1) \le \max \left \{ \frac{3t-4}{3t-1} (rn), \delta (n,r,t) \right \}$
.
Proof. Let
![]() $G$
be a
$G$
be a
![]() $K_{t+1}$
-free
$K_{t+1}$
-free
![]() $r$
-partite graph with
$r$
-partite graph with
![]() $n$
vertices in each part. If
$n$
vertices in each part. If
![]() $\delta (G)\gt \frac{3t-4}{3t-1} (rn)$
, then
$\delta (G)\gt \frac{3t-4}{3t-1} (rn)$
, then
![]() $\chi (G)\le t$
by Theorem 3.1. Thus
$\chi (G)\le t$
by Theorem 3.1. Thus
![]() $G\in \mathcal{G}(n, r, t)$
and
$G\in \mathcal{G}(n, r, t)$
and
![]() $\delta (G)\le \delta (n, r, t)$
.
$\delta (G)\le \delta (n, r, t)$
.
By applying (3.1) together with Corollary 3.2, one can conclude that
![]() $f(n,r,t+1) = \delta (n,r,t)$
provided that
$f(n,r,t+1) = \delta (n,r,t)$
provided that
![]() $r\geq (t-1)(3t-1)$
.
$r\geq (t-1)(3t-1)$
.
Corollary 3.3.
Let
![]() $r \gt t \ge 2$
and
$r \gt t \ge 2$
and
![]() $0\leq a \leq t-1$
so that
$0\leq a \leq t-1$
so that
![]() $r \equiv -a \pmod{t}$
. If
$r \equiv -a \pmod{t}$
. If
![]() $ r \ge a(3t-1)$
then
$ r \ge a(3t-1)$
then
![]() $f(n,r,t+1) = \delta (n,r,t)$
.
$f(n,r,t+1) = \delta (n,r,t)$
.
Proof. (1.2) covers the case when
![]() $a =0$
so we assume that
$a =0$
so we assume that
![]() $a \in [t-1]$
. By Corollary 3.2, it suffices to show that
$a \in [t-1]$
. By Corollary 3.2, it suffices to show that
![]() $\delta (n,r,t) \ge \frac{3t-4}{3t-1} rn$
. By (3.1), we have
$\delta (n,r,t) \ge \frac{3t-4}{3t-1} rn$
. By (3.1), we have
where we use the fact that
![]() $r \ge a(3t-1)$
in the last inequality.
$r \ge a(3t-1)$
in the last inequality.
4. Lower bound constructions
In this section, we give constructions that improve on the lower bound in (1.3) whenever
![]() $r \not \equiv 0,-1 \pmod{t}$
.
$r \not \equiv 0,-1 \pmod{t}$
.
Proposition 4.1.
Let
![]() $r \ge m,t \ge 2$
be such that
$r \ge m,t \ge 2$
be such that
![]() $m (t-1) \le r \le mt-1$
. Then there exists a graph
$m (t-1) \le r \le mt-1$
. Then there exists a graph
![]() $G \in \mathcal{G}(n,r,t)$
such that
$G \in \mathcal{G}(n,r,t)$
such that
![]() $\delta (G) = (r-1)n - (m-1) \left \lceil \frac{(r-1)n}{mt-2} \right \rceil$
. In particular,
$\delta (G) = (r-1)n - (m-1) \left \lceil \frac{(r-1)n}{mt-2} \right \rceil$
. In particular,
Proof. When
![]() $r=mt-1$
, the desired bound follows from (3.1). We thus assume
$r=mt-1$
, the desired bound follows from (3.1). We thus assume
![]() $r\le mt-2$
. Let
$r\le mt-2$
. Let
![]() $\ell \,:\!=\, \lceil (r-1)n/(mt-2) \rceil \le n$
. Let
$\ell \,:\!=\, \lceil (r-1)n/(mt-2) \rceil \le n$
. Let
![]() $K\,:\!=\,K_r(n)$
and let
$K\,:\!=\,K_r(n)$
and let
![]() $V_1, \ldots, V_{r}$
denote its parts. For
$V_1, \ldots, V_{r}$
denote its parts. For
![]() $i \in [t-1]$
, let
$i \in [t-1]$
, let
![]() $B_i \,:\!=\, \{(i-1)m+1, \ldots, im\}$
. So
$B_i \,:\!=\, \{(i-1)m+1, \ldots, im\}$
. So
![]() $B_1, \ldots, B_{t-1}$
form an equipartition of
$B_1, \ldots, B_{t-1}$
form an equipartition of
![]() $[m(t-1)]$
. For
$[m(t-1)]$
. For
![]() $i \in [t-1]$
, let
$i \in [t-1]$
, let
![]() $W_i \subset \bigcup _{j \in B_i} V_j$
be such that
$W_i \subset \bigcup _{j \in B_i} V_j$
be such that
![]() $|W_i \cap V_j| = \ell$
for
$|W_i \cap V_j| = \ell$
for
![]() $j \in B_i$
. Let
$j \in B_i$
. Let
![]() $W_t \,:\!=\, V(K) \setminus \bigcup _{i \in [t-1]}W_i$
. Then
$W_t \,:\!=\, V(K) \setminus \bigcup _{i \in [t-1]}W_i$
. Then
Let
![]() $G^{\prime}$
be the complete
$G^{\prime}$
be the complete
![]() $t$
-partite graph with parts
$t$
-partite graph with parts
![]() $W_1, \ldots, W_{t}$
. We set
$W_1, \ldots, W_{t}$
. We set
![]() $G \,:\!=\, K \cap G^{\prime}$
; that is,
$G \,:\!=\, K \cap G^{\prime}$
; that is,
![]() $G$
is the graph on
$G$
is the graph on
![]() $V(K)$
such that, for
$V(K)$
such that, for
![]() $x \in V_i \cap W_j$
and
$x \in V_i \cap W_j$
and
![]() $x^{\prime} \in V_{i^{\prime}} \cap W_{j^{\prime}}$
, we have
$x^{\prime} \in V_{i^{\prime}} \cap W_{j^{\prime}}$
, we have
![]() $xx^{\prime} \in E(G)$
if and only if
$xx^{\prime} \in E(G)$
if and only if
![]() $i \ne i^{\prime}$
and
$i \ne i^{\prime}$
and
![]() $j \ne j^{\prime}$
. Clearly
$j \ne j^{\prime}$
. Clearly
![]() $\chi (G) \le \chi (G^{\prime}) \le t$
. If
$\chi (G) \le \chi (G^{\prime}) \le t$
. If
![]() $x \in V_i$
with
$x \in V_i$
with
![]() $i \notin [m(t-1)]$
, then as
$i \notin [m(t-1)]$
, then as
![]() $x$
is only non-adjacent to the vertices in
$x$
is only non-adjacent to the vertices in
![]() $W_t$
, we have that
$W_t$
, we have that
![]() $d(x) = r n - |W_t|$
. If
$d(x) = r n - |W_t|$
. If
![]() $x \in V_i$
with
$x \in V_i$
with
![]() $i \in [m(t-1)]$
, then
$i \in [m(t-1)]$
, then
 \begin{align*} d(x) = \begin{cases} rn - (n + |W_1| - \ell ) & \text{ if } x \notin W_t,\\[4pt] rn - (n + |W_t| - ( n- \ell ) ) & \text{ if }x \in W_t. \end{cases} \end{align*}
\begin{align*} d(x) = \begin{cases} rn - (n + |W_1| - \ell ) & \text{ if } x \notin W_t,\\[4pt] rn - (n + |W_t| - ( n- \ell ) ) & \text{ if }x \in W_t. \end{cases} \end{align*}
By our choice of
![]() $\ell$
,
$\ell$
,
 \begin{align*} \delta (G) & = (r-1) n - \max \{ (m-1) \ell, (r-1)n - (m(t-1)-1) \ell \}\\[3pt] & = (r-1) n - (m-1) \ell = (r-1)n - (m-1) \left \lceil \frac{(r-1)n}{mt-2} \right \rceil, \end{align*}
\begin{align*} \delta (G) & = (r-1) n - \max \{ (m-1) \ell, (r-1)n - (m(t-1)-1) \ell \}\\[3pt] & = (r-1) n - (m-1) \ell = (r-1)n - (m-1) \left \lceil \frac{(r-1)n}{mt-2} \right \rceil, \end{align*}
as required.
Note that the lower bound in Proposition 4.1 improves the lower bound from (1.3) in the case when
![]() $r=mt-a$
with
$r=mt-a$
with
![]() $2\leq a \leq \min \{m, t-1\}$
. Indeed, in this case (1.3) gives a lower bound of
$2\leq a \leq \min \{m, t-1\}$
. Indeed, in this case (1.3) gives a lower bound of
![]() $(r-m)n$
while
$(r-m)n$
while
 \begin{align} (r-1)n - (m-1) \left \lceil \frac{(r-1)n}{mt-2} \right \rceil &\gt (r-1)n - (m-1) \frac{(r-1)}{mt-2}n-(m-1) \nonumber\\[3pt] &= (r-m)n + \frac{(a-1)(m-1)}{mt-2}n - (m-1). \end{align}
\begin{align} (r-1)n - (m-1) \left \lceil \frac{(r-1)n}{mt-2} \right \rceil &\gt (r-1)n - (m-1) \frac{(r-1)}{mt-2}n-(m-1) \nonumber\\[3pt] &= (r-m)n + \frac{(a-1)(m-1)}{mt-2}n - (m-1). \end{align}
Thus, if
![]() $n\ge (mt-2)/(a-1)$
, then the lower bound in Proposition 4.1 improves the lower bound from (1.3).
$n\ge (mt-2)/(a-1)$
, then the lower bound in Proposition 4.1 improves the lower bound from (1.3).
In the remaining case – when
![]() $m\lt a\leq t-1$
– the next result beats the lower bound from (1.3) when
$m\lt a\leq t-1$
– the next result beats the lower bound from (1.3) when
![]() $n$
is not too small.
$n$
is not too small.
Proposition 4.2.
Let
![]() $r \gt t \geq 3$
be such that
$r \gt t \geq 3$
be such that
![]() $r = mt - a$
with
$r = mt - a$
with
![]() $2\leq m \lt a\lt t$
. Then
$2\leq m \lt a\lt t$
. Then
Proof. Let
![]() $t^{\prime}\,:\!=\, t-a+m$
and
$t^{\prime}\,:\!=\, t-a+m$
and
![]() $r^{\prime} \,:\!=\, m(t^{\prime}-1)$
. By Proposition 4.1, there exists a graph
$r^{\prime} \,:\!=\, m(t^{\prime}-1)$
. By Proposition 4.1, there exists a graph
![]() $G^{\prime} \in \mathcal{G}(n,r^{\prime},t^{\prime})$
such that
$G^{\prime} \in \mathcal{G}(n,r^{\prime},t^{\prime})$
such that
where the last inequality is due to fact that
We now construct a graph
![]() $G \in \mathcal{G}(n,r,t)$
from
$G \in \mathcal{G}(n,r,t)$
from
![]() $G^{\prime}$
as follows. Let
$G^{\prime}$
as follows. Let
![]() $W_{a-m+1} \,:\!=\, V(G^{\prime})$
. Let
$W_{a-m+1} \,:\!=\, V(G^{\prime})$
. Let
![]() $W_1, \ldots, W_{a-m}$
be vertex sets each of size
$W_1, \ldots, W_{a-m}$
be vertex sets each of size
![]() $(m-1)n$
such that
$(m-1)n$
such that
![]() $W_1, \ldots, W_{a-m+1}$
are disjoint. Let
$W_1, \ldots, W_{a-m+1}$
are disjoint. Let
![]() $G$
be the resulting graph on
$G$
be the resulting graph on
![]() $\bigcup _{i \in [a-m+1]} W_i$
obtained from
$\bigcup _{i \in [a-m+1]} W_i$
obtained from
![]() $G^{\prime}$
by adding edges
$G^{\prime}$
by adding edges
![]() $xx^{\prime}$
for all
$xx^{\prime}$
for all
![]() $x \in W_i$
and
$x \in W_i$
and
![]() $x^{\prime} \in W_{i^{\prime}}$
with
$x^{\prime} \in W_{i^{\prime}}$
with
![]() $i \ne i^{\prime}$
. Note that
$i \ne i^{\prime}$
. Note that
![]() $\chi (G) = \chi (G^{\prime}) + a-m \le t$
. Since each
$\chi (G) = \chi (G^{\prime}) + a-m \le t$
. Since each
![]() $W_i$
with
$W_i$
with
![]() $i \in [a-m]$
can be partitioned into
$i \in [a-m]$
can be partitioned into
![]() $m-1$
vertex classes of size
$m-1$
vertex classes of size
![]() $n$
, we deduce that
$n$
, we deduce that
![]() $G \in \mathcal{G}(n,r,t)$
.
$G \in \mathcal{G}(n,r,t)$
.
For
![]() $x \in V(G) \setminus V(G^{\prime})$
,
$x \in V(G) \setminus V(G^{\prime})$
,
![]() $x$
is non-adjacent to the vertices in the class
$x$
is non-adjacent to the vertices in the class
![]() $W_i$
it lies in and so
$W_i$
it lies in and so
![]() $d_G(x) = r n -(m-1) n$
. For
$d_G(x) = r n -(m-1) n$
. For
![]() $x \in V(G^{\prime})$
, we have
$x \in V(G^{\prime})$
, we have
![]() $d_G(x) = (a-m)(m-1) n + d_{G^{\prime}}(x)$
and so the vertex
$d_G(x) = (a-m)(m-1) n + d_{G^{\prime}}(x)$
and so the vertex
![]() $y \in V(G^{\prime})$
with smallest degree
$y \in V(G^{\prime})$
with smallest degree
![]() $d_G(y)$
satisfies
$d_G(y)$
satisfies
Hence,
as required.
By applying Corollary 3.2 with Proposition 4.1, we can obtain the following result, which improves on Corollary 3.3 in most cases when
![]() $n$
is not too small.
$n$
is not too small.
Corollary 4.3.
Given
![]() $m, t \ge 2$
, let
$m, t \ge 2$
, let
![]() $r = mt -a$
where
$r = mt -a$
where
![]() $2 \le a \le \min \{m, t-1\}$
. If
$2 \le a \le \min \{m, t-1\}$
. If
then
![]() $f(n,r,t+1) = \delta (n,r,t)$
.
$f(n,r,t+1) = \delta (n,r,t)$
.
Proof. By (3.1) and Corollary 3.2, it suffices to prove that
Proposition 4.1 and (4.1) together imply that
On the other hand,
![]() $\frac{3t-4}{3t-1} r = r-m +\frac{a}t-\frac{r}{t(3t-1)}.$
Thus, to prove (4.2), it suffices to have
$\frac{3t-4}{3t-1} r = r-m +\frac{a}t-\frac{r}{t(3t-1)}.$
Thus, to prove (4.2), it suffices to have
Indeed, this is equivalent to our assumption
5. An upper bound on
 $\delta (n,r,t)$
$\delta (n,r,t)$
In this section, we prove the following upper bound on
![]() $ \delta (n,r,t)$
.
$ \delta (n,r,t)$
.
Proposition 5.1.
Let
![]() $r,n \in \mathbb{N}$
and
$r,n \in \mathbb{N}$
and
![]() $m,t \ge 2$
be such that
$m,t \ge 2$
be such that
![]() $(m-1)t \lt r \lt mt$
. Then,
$(m-1)t \lt r \lt mt$
. Then,
Proof. Let
![]() $\Delta ^* \,:\!=\, (m-1) (r-1)n/(mt-2)$
. Since
$\Delta ^* \,:\!=\, (m-1) (r-1)n/(mt-2)$
. Since
![]() $\delta (n,r,t)$
is an integer, it suffices to show that
$\delta (n,r,t)$
is an integer, it suffices to show that
![]() $\delta (n,r,t) \le (r-1)n - \Delta ^*$
. Suppose to the contrary that
$\delta (n,r,t) \le (r-1)n - \Delta ^*$
. Suppose to the contrary that
![]() $\delta (n,r, t) \gt (r-1)n - \Delta ^*$
. Let
$\delta (n,r, t) \gt (r-1)n - \Delta ^*$
. Let
![]() $G \in \mathcal{G}(n,r,t)$
be such that
$G \in \mathcal{G}(n,r,t)$
be such that
![]() $\delta (G) =\delta (n,r, t)$
. As
$\delta (G) =\delta (n,r, t)$
. As
![]() $G \in \mathcal{G}(n,r,t)$
,
$G \in \mathcal{G}(n,r,t)$
,
![]() $V(G)$
can be partitioned into
$V(G)$
can be partitioned into
![]() $r$
independent sets
$r$
independent sets
![]() $V_1,\ldots, V_r$
each of size
$V_1,\ldots, V_r$
each of size
![]() $n$
; as
$n$
; as
![]() $\chi (G) \le t$
,
$\chi (G) \le t$
,
![]() $V(G)$
can be partitioned into
$V(G)$
can be partitioned into
![]() $t$
colour classes
$t$
colour classes
![]() $W_1, \ldots, W_{t}$
. For every
$W_1, \ldots, W_{t}$
. For every
![]() $x\in V_i\cap W_j$
,
$x\in V_i\cap W_j$
,
![]() $x$
is non-adjacent to those vertices in
$x$
is non-adjacent to those vertices in
![]() $V_i \cup W_j$
and so
$V_i \cup W_j$
and so
![]() $d(x)\leq rn -|V_i|- |W_j|+|V_i\cap W_j| =(r-1)n - |W_j|+|V_i\cap W_j|$
.
$d(x)\leq rn -|V_i|- |W_j|+|V_i\cap W_j| =(r-1)n - |W_j|+|V_i\cap W_j|$
.
For
![]() $i\in [r]$
, let
$i\in [r]$
, let
![]() $C(i)\,:\!=\,\{j\in [t]: |V_i \cap W_j|\ne 0\}$
be the set of colours present in
$C(i)\,:\!=\,\{j\in [t]: |V_i \cap W_j|\ne 0\}$
be the set of colours present in
![]() $V_i$
. For
$V_i$
. For
![]() $j\in [t]$
, let
$j\in [t]$
, let
![]() $\text{supp}(j)\,:\!=\,\{i\in [r]: |V_i \cap W_j|\ne 0\}$
be the set of parts that colour
$\text{supp}(j)\,:\!=\,\{i\in [r]: |V_i \cap W_j|\ne 0\}$
be the set of parts that colour
![]() $j$
is present. Let
$j$
is present. Let
Thus
![]() $\delta (G)\leq \min _{j\in [t]} \{(r-1)n - \Delta _j \}$
. Hence we have for all
$\delta (G)\leq \min _{j\in [t]} \{(r-1)n - \Delta _j \}$
. Hence we have for all
![]() $j \in [t]$
,
$j \in [t]$
,
Claim 5.2.
For all
![]() $j \in [t]$
,
$j \in [t]$
,
![]() $|W_j| \lt m \Delta ^*/(m-1)$
.
$|W_j| \lt m \Delta ^*/(m-1)$
.
Proof of claim. Note that
If
![]() $|\text{supp}(j)| \le m-1$
, then
$|\text{supp}(j)| \le m-1$
, then
![]() $|W_j|\le (m-1)n \lt \frac{m}{m-1} \Delta ^*$
as desired. Hence, we may assume that
$|W_j|\le (m-1)n \lt \frac{m}{m-1} \Delta ^*$
as desired. Hence, we may assume that
![]() $|\text{supp}(j)| \ge m$
. Using the definition of
$|\text{supp}(j)| \ge m$
. Using the definition of
![]() $\Delta _j$
and (5.1), we obtain that
$\Delta _j$
and (5.1), we obtain that
Hence the claim follows.
Suppose that
![]() $|C(i)| =1$
for all
$|C(i)| =1$
for all
![]() $i \in [r]$
. Every
$i \in [r]$
. Every
![]() $V_i$
is a subset of some
$V_i$
is a subset of some
![]() $W_j$
and consequently, there exists
$W_j$
and consequently, there exists
![]() $j \in [t]$
with
$j \in [t]$
with
![]() $|W_j| \ge \lceil r/t \rceil n \ge m n$
. It follows that
$|W_j| \ge \lceil r/t \rceil n \ge m n$
. It follows that
a contradiction.
Without loss of generality, we assume that
![]() $|C(1)|=s\ge 2$
. For every
$|C(1)|=s\ge 2$
. For every
![]() $j \in C(1)$
, we know that
$j \in C(1)$
, we know that
![]() $|W_j| \le \Delta _j + |V_1 \cap W_j|$
from the definition of
$|W_j| \le \Delta _j + |V_1 \cap W_j|$
from the definition of
![]() $\Delta _j$
. Hence,
$\Delta _j$
. Hence,
Together with Claim 5.2, this gives
a contradiction.
6. Proof of the main results
The proofs of Theorems 1.2 and 1.3 and Corollary 1.4 now follow easily from our auxiliary results.
Proof of Theorem 1.2. The
![]() $m=2$
case of the theorem is precisely Lemma 2.1. For
$m=2$
case of the theorem is precisely Lemma 2.1. For
![]() $m\geq 3$
, we may apply Corollary 3.3 (with
$m\geq 3$
, we may apply Corollary 3.3 (with
![]() $a\,:\!=\,1$
) to conclude that
$a\,:\!=\,1$
) to conclude that
![]() $f(n,r,t+1)=\delta (n,r,t)$
. Then Proposition 5.1 implies
$f(n,r,t+1)=\delta (n,r,t)$
. Then Proposition 5.1 implies
![]() $\delta (n,r,t)\leq (r-m)n=(r-\lceil r/t \rceil )n$
; together with the lower bound in (1.3) this completes the proof.
$\delta (n,r,t)\leq (r-m)n=(r-\lceil r/t \rceil )n$
; together with the lower bound in (1.3) this completes the proof.
Proof of Theorem 1.3. Under Condition (i), we first apply Corollary 3.3 to obtain that
![]() $f(n,r,t+1)=\delta (n,r,t)$
. Then Propositions 4.1 and 5.1 give the desired lower and upper bounds, respectively. Under Condition (ii), we apply Corollary 4.3 instead of Corollary 3.3.
$f(n,r,t+1)=\delta (n,r,t)$
. Then Propositions 4.1 and 5.1 give the desired lower and upper bounds, respectively. Under Condition (ii), we apply Corollary 4.3 instead of Corollary 3.3.
Proof of Corollary 1.4. The case when
![]() $r \equiv 0 \pmod{3}$
follows from (1.2). The case when
$r \equiv 0 \pmod{3}$
follows from (1.2). The case when
![]() $r \equiv 2 \pmod{3}$
follows immediately from Theorem 1.2. If
$r \equiv 2 \pmod{3}$
follows immediately from Theorem 1.2. If
![]() $r \equiv 1 \pmod{3}$
then
$r \equiv 1 \pmod{3}$
then
![]() $r=3m-2$
for some
$r=3m-2$
for some
![]() $m \geq 4$
. Thus Condition (i) of Theorem 1.3 holds provided that
$m \geq 4$
. Thus Condition (i) of Theorem 1.3 holds provided that
![]() $m \geq 6$
. If
$m \geq 6$
. If
![]() $r=10$
and
$r=10$
and
![]() $n \geq 60$
or
$n \geq 60$
or
![]() $r=13$
and
$r=13$
and
![]() $n \geq 22$
, then it is easy to check that Condition (ii) of Theorem 1.3 holds. Thus, Theorem 1.3 yields the corollary in this case.
$n \geq 22$
, then it is easy to check that Condition (ii) of Theorem 1.3 holds. Thus, Theorem 1.3 yields the corollary in this case.
7. Concluding remarks
In this article, we have resolved Problem 1.1 for many choices of
![]() $r$
and
$r$
and
![]() $t$
. For the remaining open cases, it would be interesting to establish when (if at all) a lower bound construction from Section 4 is extremal. One obvious case would be to determine
$t$
. For the remaining open cases, it would be interesting to establish when (if at all) a lower bound construction from Section 4 is extremal. One obvious case would be to determine
![]() $f(n,7,4)$
, which is the only remaining case for
$f(n,7,4)$
, which is the only remaining case for
![]() $f(n,r,4)$
.
$f(n,r,4)$
.
Our results show that
![]() $f(n,r,t+1)=\delta (n,r,t)$
when
$f(n,r,t+1)=\delta (n,r,t)$
when
![]() $r$
is large compared to
$r$
is large compared to
![]() $t$
. It would be interesting to determine all values of
$t$
. It would be interesting to determine all values of
![]() $r$
and
$r$
and
![]() $t$
for which this equality holds. Proposition 5.1 and (1.1) together show that
$t$
for which this equality holds. Proposition 5.1 and (1.1) together show that
![]() $f(n, t+1, t+1)\gt \delta (n, t+1, t)$
when
$f(n, t+1, t+1)\gt \delta (n, t+1, t)$
when
![]() $t\ge 3$
is odd and
$t\ge 3$
is odd and
![]() $n$
is sufficiently large. Indeed, Proposition 5.1 implies that
$n$
is sufficiently large. Indeed, Proposition 5.1 implies that
![]() $\delta (n, t+1, t)\le tn - \lceil \frac{tn}{2t-2}\rceil$
for every
$\delta (n, t+1, t)\le tn - \lceil \frac{tn}{2t-2}\rceil$
for every
![]() $t\ge 2$
. If
$t\ge 2$
. If
![]() $t$
is odd, then by (1.1), we have
$t$
is odd, then by (1.1), we have
As mentioned in the Introduction, Bollobás, Erdős, and Straus [Reference Bollobás, Erdős and Straus4] determined the largest
![]() $\delta (G)$
among all
$\delta (G)$
among all
![]() $K_3$
-free (not necessarily balanced)
$K_3$
-free (not necessarily balanced)
![]() $r$
-partite graphs
$r$
-partite graphs
![]() $G$
for all
$G$
for all
![]() $r$
. It is natural to extend the results in the present paper to unbalanced multipartite graphs as well.
$r$
. It is natural to extend the results in the present paper to unbalanced multipartite graphs as well.
It is also natural to ask for the largest
![]() $\delta (G)$
among
$\delta (G)$
among
![]() $H$
-free multipartite graphs
$H$
-free multipartite graphs
![]() $G$
for a fixed graph
$G$
for a fixed graph
![]() $H\ne K_t$
. For example, Bollobás, Erdős, and Szemerédi [Reference Bollobás, Erdős and Szemerédi5] showed that if
$H\ne K_t$
. For example, Bollobás, Erdős, and Szemerédi [Reference Bollobás, Erdős and Szemerédi5] showed that if
![]() $G$
is a tripartite graph with
$G$
is a tripartite graph with
![]() $n$
vertices in each part and with
$n$
vertices in each part and with
![]() $\delta (G)\ge n + \frac{1}{\sqrt{2}} n^{3/4}$
, then
$\delta (G)\ge n + \frac{1}{\sqrt{2}} n^{3/4}$
, then
![]() $G$
contains a copy of
$G$
contains a copy of
![]() $K_3(2)$
; they asked if
$K_3(2)$
; they asked if
![]() $\delta (G)\ge n + C n^{1/2}$
suffices. Furthermore, extending the aforementioned multipartite Turán theorem of Bollobás, Erdős, and Straus [Reference Bollobás, Erdős and Straus4], there has been recent work on determining the largest
$\delta (G)\ge n + C n^{1/2}$
suffices. Furthermore, extending the aforementioned multipartite Turán theorem of Bollobás, Erdős, and Straus [Reference Bollobás, Erdős and Straus4], there has been recent work on determining the largest
![]() $e(G)$
among all multipartite graphs
$e(G)$
among all multipartite graphs
![]() $G$
on
$G$
on
![]() $n$
vertices that contain no multiple (disjoint) copies of
$n$
vertices that contain no multiple (disjoint) copies of
![]() $K_t$
, see, e.g., [Reference Bennett, English and Talanda-Fisher3, Reference Han and Zhao8].
$K_t$
, see, e.g., [Reference Bennett, English and Talanda-Fisher3, Reference Han and Zhao8].
The following result might be useful for constructing extremal examples for the remaining open cases of Problem 1.1. It shows that given an upper bound on
![]() $\Delta (n_0,r_0,t_0)/n_0$
one can obtain an upper bound on
$\Delta (n_0,r_0,t_0)/n_0$
one can obtain an upper bound on
![]() $\Delta (n,r,t)/n$
for other triples
$\Delta (n,r,t)/n$
for other triples
![]() $(n,r,t)$
.
$(n,r,t)$
.
Proposition 7.1.
Let
![]() $r_0, t_0 \in \mathbb N$
so that
$r_0, t_0 \in \mathbb N$
so that
![]() $2\leq t_0 \leq r_0$
. Let
$2\leq t_0 \leq r_0$
. Let
![]() $\Delta _0\geq 0$
be such that
$\Delta _0\geq 0$
be such that
![]() $\Delta (n_0,r_0,t_0)/n_0 \leq \Delta _0$
for all
$\Delta (n_0,r_0,t_0)/n_0 \leq \Delta _0$
for all
![]() $n_0 \in \mathbb N$
. Let
$n_0 \in \mathbb N$
. Let
![]() $n,k \geq 2$
be integers. Set
$n,k \geq 2$
be integers. Set
![]() $r\,:\!=\,r_0k$
and
$r\,:\!=\,r_0k$
and
![]() $t\,:\!=\,k+t_0$
. Then there exists an
$t\,:\!=\,k+t_0$
. Then there exists an
![]() $r$
-partite graph
$r$
-partite graph
![]() $G$
with parts of size
$G$
with parts of size
![]() $n$
so that:
$n$
so that:
-
 $G$
contains no crossing independent set of size
$G$
contains no crossing independent set of size
 $t$
;
$t$
; -
 $\Delta (G) \leq (r_0-1)\left \lceil \dfrac{\Delta _0+(k-1)r_0}{\Delta _0+kr_0-1} \cdot n \right \rceil$
.
$\Delta (G) \leq (r_0-1)\left \lceil \dfrac{\Delta _0+(k-1)r_0}{\Delta _0+kr_0-1} \cdot n \right \rceil$
.
That is,
or equivalently
Proof. Let
![]() $\ell \,:\!=\, \lfloor (r_0-1)n/(\Delta _0+kr_0-1) \rfloor$
. We construct an
$\ell \,:\!=\, \lfloor (r_0-1)n/(\Delta _0+kr_0-1) \rfloor$
. We construct an
![]() $r$
-partite graph
$r$
-partite graph
![]() $G$
with parts
$G$
with parts
![]() $V_1, \ldots, V_{r}$
of size
$V_1, \ldots, V_{r}$
of size
![]() $n$
as follows. Partition each
$n$
as follows. Partition each
![]() $V_i$
into
$V_i$
into
![]() $L_i\cup S_i$
such that
$L_i\cup S_i$
such that
![]() $|S_i| = \ell$
and
$|S_i| = \ell$
and
![]() $|L_i| = n-\ell$
. We call the vertices in each
$|L_i| = n-\ell$
. We call the vertices in each
![]() $L_i$
large and those in each
$L_i$
large and those in each
![]() $S_i$
small. We partition
$S_i$
small. We partition
![]() $[r]$
into
$[r]$
into
![]() $k$
blocks of size
$k$
blocks of size
![]() $r_0$
by assigning
$r_0$
by assigning
![]() $i$
and
$i$
and
![]() $j$
to the same block if
$j$
to the same block if
![]() $\lceil i/r_0 \rceil = \lceil j/r_0 \rceil$
. We form a complete bipartite graph between
$\lceil i/r_0 \rceil = \lceil j/r_0 \rceil$
. We form a complete bipartite graph between
![]() $L_i$
and
$L_i$
and
![]() $L_j$
(joining
$L_j$
(joining
![]() $L_i$
and
$L_i$
and
![]() $L_j$
for short) if and only if
$L_j$
for short) if and only if
![]() $i$
and
$i$
and
![]() $j$
are in the same block. We join
$j$
are in the same block. We join
![]() $S_i$
and
$S_i$
and
![]() $S_j$
if
$S_j$
if
![]() $i$
and
$i$
and
![]() $j$
are not in the same block. By the definition of
$j$
are not in the same block. By the definition of
![]() $\Delta _0$
, there exists an
$\Delta _0$
, there exists an
![]() $r_0$
-partite graph
$r_0$
-partite graph
![]() $G_S$
with
$G_S$
with
![]() $\ell$
vertices in each part and
$\ell$
vertices in each part and
![]() $\Delta (G_S) \leq \Delta _0 \ell$
containing no crossing independent set of size
$\Delta (G_S) \leq \Delta _0 \ell$
containing no crossing independent set of size
![]() $t_0$
. We place a copy of
$t_0$
. We place a copy of
![]() $G_S$
in each block so that the sets
$G_S$
in each block so that the sets
![]() $S_i$
in the block each form one of the vertex classes of
$S_i$
in the block each form one of the vertex classes of
![]() $G_S$
.
$G_S$
.
We claim that
![]() $G$
contains no crossing independent set of size
$G$
contains no crossing independent set of size
![]() $t$
. Indeed, a crossing independent set contains at most one large vertex from each block, and at most
$t$
. Indeed, a crossing independent set contains at most one large vertex from each block, and at most
![]() $t_0-1$
small vertices. Thus, the largest crossing independent set has size
$t_0-1$
small vertices. Thus, the largest crossing independent set has size
![]() $k+t_0-1 = t-1$
.
$k+t_0-1 = t-1$
.
Note that
The choice of
![]() $\ell$
ensures
$\ell$
ensures
as desired.
Acknowledgment
The authors are grateful to the referees for their helpful and careful reviews.