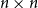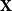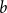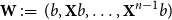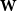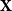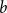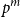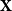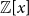1. Introduction
What information about a graph is encoded in the spectrum of its adjacency matrix? A well-known conjecture by van Dam and Haemers [Reference van Dam and Haemers24] suggests that the answer to this question is all information in the typical case in the sense that almost all graphs are determined up to isomorphism by their spectrum. Unfortunately, progress towards that conjecture has been fairly limited due to the fact that there are essentially no known general-purpose methods to prove that a graph is determined by its spectrum. There are many more proof techniques available to prove that a graph’s spectrum does not determine it than to show that it does [Reference Abiad and Haemers1, Reference Butler2, Reference Godsil and McKay8, Reference Halbeisen and Hungerbühler10, Reference Schwenk21].
In view of this, it is intriguing that a sufficient condition for generalised spectral determinacy was discovered in 2006 by Wang and Xu [Reference Wang and Xu29, Reference Wang and Xu30]. The generalised spectrum of a graph
![]() $G$
here refers to the ordered pair
$G$
here refers to the ordered pair
![]() $(\textrm{spec}({\mathbf{A}}), \textrm{spec}({\mathbf{A}^{\mkern-1mu {c}}}))$
consisting of the spectra of the adjacency matrix
$(\textrm{spec}({\mathbf{A}}), \textrm{spec}({\mathbf{A}^{\mkern-1mu {c}}}))$
consisting of the spectra of the adjacency matrix
![]() $\mathbf{A}$
of
$\mathbf{A}$
of
![]() $G$
and of the adjacency matrix
$G$
and of the adjacency matrix
![]() ${\mathbf{A}^{\mkern-1mu {c}}}$
of its complement graph. Refinements of the results of [Reference Wang and Xu29, Reference Wang and Xu30] have given rise to an active area of research in recent years; see, for example, [Reference Li and Sun12, Reference Qiu, Wang and Wang17, Reference Qiu, Wang and Zhang18, Reference Wang26–Reference Wang and Wang28]. For definiteness, let us state a refinement that is particularly insightful and motivates the results of the current paper.
${\mathbf{A}^{\mkern-1mu {c}}}$
of its complement graph. Refinements of the results of [Reference Wang and Xu29, Reference Wang and Xu30] have given rise to an active area of research in recent years; see, for example, [Reference Li and Sun12, Reference Qiu, Wang and Wang17, Reference Qiu, Wang and Zhang18, Reference Wang26–Reference Wang and Wang28]. For definiteness, let us state a refinement that is particularly insightful and motivates the results of the current paper.
Define a matrix with integer entries by
![]() ${\mathbf{W}} \,:\!=\, ({\mathbf{A}}^{j-1}e)_{j=1}^n$
where
${\mathbf{W}} \,:\!=\, ({\mathbf{A}}^{j-1}e)_{j=1}^n$
where
![]() $e = (1,\ldots, 1)^{\textrm{T}}$
is the all-ones vector and
$e = (1,\ldots, 1)^{\textrm{T}}$
is the all-ones vector and
![]() $n$
is the number of vertices of
$n$
is the number of vertices of
![]() $G$
. Let
$G$
. Let
![]() $\textrm{coker}({\mathbf{W}}) \,:\!=\,{\mathbb{Z}}^n/{\mathbf{W}}({\mathbb{Z}}^n)$
denote the cokernel of this matrix. Then, the following is an equivalent rephrasing of [Reference Wang27, Theorem 1.1]; see [Reference Qiu, Wang and Zhang18, p. 2].
$\textrm{coker}({\mathbf{W}}) \,:\!=\,{\mathbb{Z}}^n/{\mathbf{W}}({\mathbb{Z}}^n)$
denote the cokernel of this matrix. Then, the following is an equivalent rephrasing of [Reference Wang27, Theorem 1.1]; see [Reference Qiu, Wang and Zhang18, p. 2].
Theorem 1.1 (Wang, [Reference Wang27]). Let
![]() $G$
be a simple graph. Assume that there exists an odd and square-free integer
$G$
be a simple graph. Assume that there exists an odd and square-free integer
![]() $m$
such that
$m$
such that
as an Abelian group. Then,
![]() $G$
is determined by its generalised spectrum up to isomorphism.
$G$
is determined by its generalised spectrum up to isomorphism.
It is believed that the conditions of Theorem 1.1 are satisfied for a nonvanishing fraction of all simple graphs [Reference Wang27, Conjecture 2]. For comparison, the best known bound on the non-generalised problem is due to Koval and Kwan [Reference Koval and Kwan11], who recently established that there are at least
![]() $e^{cn}$
graphs on
$e^{cn}$
graphs on
![]() $n$
vertices that are determined by their spectrum. The result from [Reference Koval and Kwan11] represents a significant improvement relative to the previous long-standing barrier of
$n$
vertices that are determined by their spectrum. The result from [Reference Koval and Kwan11] represents a significant improvement relative to the previous long-standing barrier of
![]() $e^{c\sqrt{n}}$
but still only yields a quickly vanishing fraction of all
$e^{c\sqrt{n}}$
but still only yields a quickly vanishing fraction of all
![]() $(1-o(1))2^{n(n-1)/2}/n!$
simple graphs. So, a nonvanishing fraction being determined by (generalised) spectrum would signify a remarkable development.
$(1-o(1))2^{n(n-1)/2}/n!$
simple graphs. So, a nonvanishing fraction being determined by (generalised) spectrum would signify a remarkable development.
However, even though criteria for generalised spectral determinacy have been known for almost 20 years now, it remains an open problem to prove that the criteria are indeed frequently satisfied. The current state of knowledge on the frequency of satisfaction is mostly limited to numerical studies [Reference Haemers and Spence9, Reference van Dam and Haemers24, Reference Wang27, Reference Wang and Wang28]. The lack of theoretical work is surprising given that criteria for generalised spectral determinacy are an active area of research. A possible explanation is that it is not clear what proof techniques could be used. The current paper develops a novel line of attack by making a connection to proof techniques [Reference Cheong and Yu3, Reference Nguyen and Paquette14, Reference Sawin and Wood20, Reference Wood33], which were historically developed in the context of Cohen–Lenstra heuristics for the class groups of number fields [Reference Cohen and Lenstra5] and in the study of sandpile groups of random graphs [Reference Clancy, Kaplan, Leake, Payne and Wood4].
The problem is too challenging to solve in a single step, so we direct our efforts to a variant which is more convenient for technical reasons. Instead of simple graphs, we study random directed graphs with random edge weights. Concretely, given a
![]() ${\mathbb{Z}}^{n\times n}$
-valued random matrix
${\mathbb{Z}}^{n\times n}$
-valued random matrix
![]() $\mathbf{X}$
with independent entries and a vector
$\mathbf{X}$
with independent entries and a vector
![]() $b\in{\mathbb{Z}}^n$
, we study the cokernel of the associated walk matrix
$b\in{\mathbb{Z}}^n$
, we study the cokernel of the associated walk matrix
![]() ${\mathbf{W}} \,:\!=\, ({\mathbf{X}}^{j-1} b)_{j=1}^{n}$
. To explain the terminology, note that if
${\mathbf{W}} \,:\!=\, ({\mathbf{X}}^{j-1} b)_{j=1}^{n}$
. To explain the terminology, note that if
![]() $\mathbf{X}$
is
$\mathbf{X}$
is
![]() $\{0,1 \}^{n\times n}$
-valued and interpreted as the directed adjacency matrix of a directed graph and
$\{0,1 \}^{n\times n}$
-valued and interpreted as the directed adjacency matrix of a directed graph and
![]() $b =\mathbb{1}_S$
is the indicator vector of a subset
$b =\mathbb{1}_S$
is the indicator vector of a subset
![]() $S\subseteq \{1,\ldots, n \}$
, then
$S\subseteq \{1,\ldots, n \}$
, then
![]() ${\mathbf{W}}_{i,j}$
counts the number of walks of length
${\mathbf{W}}_{i,j}$
counts the number of walks of length
![]() $j-1$
starting from
$j-1$
starting from
![]() $i$
with an endpoint in
$i$
with an endpoint in
![]() $S$
. Walk matrices of this kind are also of independent interest due to applications to control theory [Reference Godsil7, Reference O’Rourke and Touri16, Reference Sundaram and Hadjicostis22] and graph isomorphism problems [Reference Godsil7, Reference Liu and Siemons13, Reference Verbitsky and Zhukovskii25].
$S$
. Walk matrices of this kind are also of independent interest due to applications to control theory [Reference Godsil7, Reference O’Rourke and Touri16, Reference Sundaram and Hadjicostis22] and graph isomorphism problems [Reference Godsil7, Reference Liu and Siemons13, Reference Verbitsky and Zhukovskii25].
In future work, it would be interesting to pursue extensions of our results to the setting of simple graphs where Theorem 1.1 is applicable.Footnote 1 The adjacency matrix of an undirected random graph has to be symmetric, so its entries cannot be independent, which makes the problem more difficult. We expect that our proof techniques will still give insights provided that appropriate modifications are made, but these modifications pose a nontrivial challenge; see Section 4.
1.1 Results
Given an Abelian group
![]() $H$
and a prime power
$H$
and a prime power
![]() $p^m$
, we denote
$p^m$
, we denote
![]() $H_{p^m} \,:\!=\, H/p^mH$
. Then, the condition of Theorem 1.1 is satisfied if and only if
$H_{p^m} \,:\!=\, H/p^mH$
. Then, the condition of Theorem 1.1 is satisfied if and only if
![]() $\textrm{coker}({\mathbf{W}})_{p^2} \in \{0,{\mathbb{Z}}/p{\mathbb{Z}} \}$
for every odd prime
$\textrm{coker}({\mathbf{W}})_{p^2} \in \{0,{\mathbb{Z}}/p{\mathbb{Z}} \}$
for every odd prime
![]() $p$
and
$p$
and
![]() $\textrm{coker}({\mathbf{W}})_{2^2} \cong ({\mathbb{Z}}/2{\mathbb{Z}})^{\lfloor n/2\rfloor }$
. To determine how frequently Theorem 1.1 is applicable, it hence suffices to study the joint distribution of
$\textrm{coker}({\mathbf{W}})_{2^2} \cong ({\mathbb{Z}}/2{\mathbb{Z}})^{\lfloor n/2\rfloor }$
. To determine how frequently Theorem 1.1 is applicable, it hence suffices to study the joint distribution of
![]() $\textrm{coker}({\mathbf{W}})_{p^2}$
over all primes
$\textrm{coker}({\mathbf{W}})_{p^2}$
over all primes
![]() $p$
when
$p$
when
![]() $\mathbf{X}$
is the adjacency matrix of an undirected Erdős–Rényi random graph and
$\mathbf{X}$
is the adjacency matrix of an undirected Erdős–Rényi random graph and
![]() $b=e$
.
$b=e$
.
In a directed and weighted setting, the following result gives a remarkably simple formula for the limiting marginal distribution for a single prime
![]() $p$
:
$p$
:
Theorem 1.2.
Fix a prime
![]() $p$
and an integer
$p$
and an integer
![]() $m\geq 1$
. For every
$m\geq 1$
. For every
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $\mathbf{X}$
be a
$\mathbf{X}$
be a
![]() ${\mathbb{Z}}^{n\times n}$
-valued random matrix with independent
${\mathbb{Z}}^{n\times n}$
-valued random matrix with independent
![]() ${\operatorname{Unif}}\{0,1,\ldots, p^{m} - 1\}$
-distributed entries, and let
${\operatorname{Unif}}\{0,1,\ldots, p^{m} - 1\}$
-distributed entries, and let
![]() $b\in{\mathbb{Z}}^{n}$
be a deterministic vector with
$b\in{\mathbb{Z}}^{n}$
be a deterministic vector with
![]() $b\not \equiv 0 \bmod p$
.
$b\not \equiv 0 \bmod p$
.
Fix some
![]() $\ell \geq 1$
and
$\ell \geq 1$
and
![]() $0 = \lambda _0 \leq \lambda _1 \leq \cdots \leq \lambda _\ell \leq m$
. Let
$0 = \lambda _0 \leq \lambda _1 \leq \cdots \leq \lambda _\ell \leq m$
. Let
![]() $i_0\,:\!=\, \#\{i\leq \ell \,:\, \lambda _i = m \}$
and denote
$i_0\,:\!=\, \#\{i\leq \ell \,:\, \lambda _i = m \}$
and denote
![]() $\delta _j \,:\!=\, \lambda _{\ell -j+1} - \lambda _{\ell -j}$
. Then, as Abelian groups,
$\delta _j \,:\!=\, \lambda _{\ell -j+1} - \lambda _{\ell -j}$
. Then, as Abelian groups,
 \begin{align*} \lim _{n\to \infty }{\mathbb{P}}\left({\operatorname{coker}}({\mathbf{W}})_{p^m} \cong \bigoplus _{i=1}^\ell \frac{{\mathbb{Z}}}{p^{\lambda _i}{\mathbb{Z}}}\right) = \prod _{i=i_0}^\infty \left(1-p^{-(i+1)}\right)\prod _{j=1}^\ell p^{-j \delta _j}. \end{align*}
\begin{align*} \lim _{n\to \infty }{\mathbb{P}}\left({\operatorname{coker}}({\mathbf{W}})_{p^m} \cong \bigoplus _{i=1}^\ell \frac{{\mathbb{Z}}}{p^{\lambda _i}{\mathbb{Z}}}\right) = \prod _{i=i_0}^\infty \left(1-p^{-(i+1)}\right)\prod _{j=1}^\ell p^{-j \delta _j}. \end{align*}
Note in particular that Theorem 1.2 predicts that
![]() $\textrm{coker}({\mathbf{W}})_{p^2}\in \{0,{\mathbb{Z}}/p{\mathbb{Z}} \}$
with nonvanishing probability, at least for random directed and weighted graphs. For example, the limiting probabilities associated with the primes
$\textrm{coker}({\mathbf{W}})_{p^2}\in \{0,{\mathbb{Z}}/p{\mathbb{Z}} \}$
with nonvanishing probability, at least for random directed and weighted graphs. For example, the limiting probabilities associated with the primes
![]() $p=3$
,
$p=3$
,
![]() $5$
, and
$5$
, and
![]() $7$
are approximately
$7$
are approximately
![]() $0.75$
,
$0.75$
,
![]() $0.91$
, and
$0.91$
, and
![]() $0.96$
, respectively. We here emphasise odd primes because, while Theorem 1.2 also applies when
$0.96$
, respectively. We here emphasise odd primes because, while Theorem 1.2 also applies when
![]() $p=2$
, it is known that the distribution of
$p=2$
, it is known that the distribution of
![]() $\textrm{coker}({\mathbf{W}})_{2^m}$
is very different for simple and non-simple graphs; see Section 4. It would hence be ill-advised to use directed graphs as a model for the condition
$\textrm{coker}({\mathbf{W}})_{2^m}$
is very different for simple and non-simple graphs; see Section 4. It would hence be ill-advised to use directed graphs as a model for the condition
![]() $\textrm{coker}({\mathbf{W}})_{2^2} \cong ({\mathbb{Z}}/2{\mathbb{Z}})^{\lfloor n/2 \rfloor }$
.
$\textrm{coker}({\mathbf{W}})_{2^2} \cong ({\mathbb{Z}}/2{\mathbb{Z}})^{\lfloor n/2 \rfloor }$
.
The proof of Theorem 1.2 relies on interpretable combinatorial arguments. The downside is that the distributional assumption on the entries of
![]() $\mathbf{X}$
plays a crucial role, which makes the approach unsuitable for the study of unweighted graphs. Fortunately, a different proof approach allows us to study
$\mathbf{X}$
plays a crucial role, which makes the approach unsuitable for the study of unweighted graphs. Fortunately, a different proof approach allows us to study
![]() $\textrm{coker}({\mathbf{W}})$
in a general setting, which also covers the case where
$\textrm{coker}({\mathbf{W}})$
in a general setting, which also covers the case where
![]() $\mathbf{X}$
has
$\mathbf{X}$
has
![]() $\{0,1 \}$
-valued entries. Additionally, this allows us to gain insight on the joint law across different primes, and the result even applies to sparse graphs.
$\{0,1 \}$
-valued entries. Additionally, this allows us to gain insight on the joint law across different primes, and the result even applies to sparse graphs.
For this more general setting, it turns out to be essential to interact with all canonical structure on
![]() $\textrm{coker}({\mathbf{W}})$
. Equip
$\textrm{coker}({\mathbf{W}})$
. Equip
![]() ${\mathbb{Z}}^n$
with the
${\mathbb{Z}}^n$
with the
![]() ${\mathbb{Z}}[x]$
-module structure defined by
${\mathbb{Z}}[x]$
-module structure defined by
![]() $xv \,:\!=\,{\mathbf{X}} v$
, and note that
$xv \,:\!=\,{\mathbf{X}} v$
, and note that
![]() ${\mathbf{W}}({\mathbb{Z}}^n)$
is precisely the
${\mathbf{W}}({\mathbb{Z}}^n)$
is precisely the
![]() ${\mathbb{Z}}[x]$
-submodule of
${\mathbb{Z}}[x]$
-submodule of
![]() ${\mathbb{Z}}^n$
generated by
${\mathbb{Z}}^n$
generated by
![]() $b$
. Hence, the quotient
$b$
. Hence, the quotient
![]() $\textrm{coker}({\mathbf{W}})$
is canonically equipped with the structure of a
$\textrm{coker}({\mathbf{W}})$
is canonically equipped with the structure of a
![]() ${\mathbb{Z}}[x]$
-module. We require some additional notation. Let
${\mathbb{Z}}[x]$
-module. We require some additional notation. Let
![]() $Q(x)\in{\mathbb{Z}}[x]$
be a monic polynomial and consider a prime power
$Q(x)\in{\mathbb{Z}}[x]$
be a monic polynomial and consider a prime power
![]() $p^m$
. Then, given a
$p^m$
. Then, given a
![]() ${\mathbb{Z}}[x]$
-module
${\mathbb{Z}}[x]$
-module
![]() $N$
, we define a quotient module by
$N$
, we define a quotient module by
![]() $N_{p^m, Q} \,:\!=\, N/(p^mN + Q(x)N)$
. We further abbreviate
$N_{p^m, Q} \,:\!=\, N/(p^mN + Q(x)N)$
. We further abbreviate
![]() $R_{p^m,Q} \,:\!=\,{\mathbb{Z}}[x]/(p^m{\mathbb{Z}}[x] + Q(x){\mathbb{Z}}[x])$
.
$R_{p^m,Q} \,:\!=\,{\mathbb{Z}}[x]/(p^m{\mathbb{Z}}[x] + Q(x){\mathbb{Z}}[x])$
.
Fix a finite collection of prime numbers
![]() $\mathscr{P}$
and consider a scalar
$\mathscr{P}$
and consider a scalar
![]() $\alpha \gt 0$
. Then, a
$\alpha \gt 0$
. Then, a
![]() $\mathbb{Z}$
-valued random variable
$\mathbb{Z}$
-valued random variable
![]() $Y$
is said to be
$Y$
is said to be
![]() $\alpha$
-balanced mod
$\alpha$
-balanced mod
![]() $\mathscr{P}$
if for all
$\mathscr{P}$
if for all
![]() $p \in \mathscr{P}$
and
$p \in \mathscr{P}$
and
![]() $y \in{\mathbb{Z}}/p{\mathbb{Z}}$
,
$y \in{\mathbb{Z}}/p{\mathbb{Z}}$
,
Given a ring
![]() $R$
, recall that
$R$
, recall that
![]() $\textrm{Ext}^{1}_R(N,M)$
denotes the set of extensions of an
$\textrm{Ext}^{1}_R(N,M)$
denotes the set of extensions of an
![]() $R$
-modules
$R$
-modules
![]() $N$
by an
$N$
by an
![]() $R$
-module
$R$
-module
![]() $M$
[Reference Weibel31, p. 77], and denote
$M$
[Reference Weibel31, p. 77], and denote
![]() ${\textrm{Aut}}_R(N)$
and
${\textrm{Aut}}_R(N)$
and
![]() ${\textrm{Hom}}_R(N,M)$
for the sets of
${\textrm{Hom}}_R(N,M)$
for the sets of
![]() $R$
-module automorphisms and homomorphisms, respectively.
$R$
-module automorphisms and homomorphisms, respectively.
Theorem 1.3.
Fix a finite set of primes
![]() $\mathscr{P}$
. For every
$\mathscr{P}$
. For every
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $\mathbf{X}$
be a
$\mathbf{X}$
be a
![]() ${\mathbb{Z}}^{n\times n}$
-valued random matrix with independent entries, not necessarily identically distributed, such that each entry
${\mathbb{Z}}^{n\times n}$
-valued random matrix with independent entries, not necessarily identically distributed, such that each entry
![]() ${\mathbf{X}}_{i,j}$
is
${\mathbf{X}}_{i,j}$
is
![]() $\alpha _n$
-balanced mod
$\alpha _n$
-balanced mod
![]() $\mathscr{P}$
. Further, let
$\mathscr{P}$
. Further, let
![]() $b\in{\mathbb{Z}}^{n}$
be deterministic with
$b\in{\mathbb{Z}}^{n}$
be deterministic with
![]() $b\not \equiv 0\bmod p$
for every
$b\not \equiv 0\bmod p$
for every
![]() $p\in \mathscr{P}$
.
$p\in \mathscr{P}$
.
Assume that
![]() $\lim _{n\to \infty } n\alpha _n/\ln (n) = \infty$
. Then, for every integer
$\lim _{n\to \infty } n\alpha _n/\ln (n) = \infty$
. Then, for every integer
![]() $m\geq 1$
, monic polynomial
$m\geq 1$
, monic polynomial
![]() $Q\in{\mathbb{Z}}[x]$
of degree
$Q\in{\mathbb{Z}}[x]$
of degree
![]() $\geq 1$
, and collection of finite
$\geq 1$
, and collection of finite
![]() $R_{p^m,Q}$
-modules
$R_{p^m,Q}$
-modules
![]() $N_{p^m,Q}$
:
$N_{p^m,Q}$
:
-
(1) The quotients
 ${\operatorname{coker}}({\mathbf{W}})_{p^m,Q}$
associated with different primes
${\operatorname{coker}}({\mathbf{W}})_{p^m,Q}$
associated with different primes
 $p\in \mathscr{P}$
are asymptotically independent. More precisely, as
$p\in \mathscr{P}$
are asymptotically independent. More precisely, as
 ${\mathbb{Z}}[x]$
-modules,
for certain probability measures
${\mathbb{Z}}[x]$
-modules,
for certain probability measures \begin{align*} \lim _{n\to \infty }{\mathbb{P}}\bigl (\forall p\in \mathscr{P}\,:\,{\operatorname{coker}}({\mathbf{W}})_{p^m,Q} \cong N_{p^m,Q} \bigr ) = \prod _{p\in \mathscr{P}}\mu _{p^m,Q}(N_{p^m,Q} ) \end{align*}
\begin{align*} \lim _{n\to \infty }{\mathbb{P}}\bigl (\forall p\in \mathscr{P}\,:\,{\operatorname{coker}}({\mathbf{W}})_{p^m,Q} \cong N_{p^m,Q} \bigr ) = \prod _{p\in \mathscr{P}}\mu _{p^m,Q}(N_{p^m,Q} ) \end{align*}
 $\mu _{p^m,Q}$
supported on finite
$\mu _{p^m,Q}$
supported on finite
 $R_{p^m,Q}$
-modules.
$R_{p^m,Q}$
-modules.
-
(2) Suppose that
 $Q(x) \equiv \prod _{i=1}^{r_p} Q_{i,p}(x)^{q_{i,p}} \bmod p$
is the unique factorisation of
$Q(x) \equiv \prod _{i=1}^{r_p} Q_{i,p}(x)^{q_{i,p}} \bmod p$
is the unique factorisation of
 $Q\bmod p$
into powers of distinct monic irreducible polynomials
$Q\bmod p$
into powers of distinct monic irreducible polynomials
 $Q_{i,p} \in{\mathbb{F}}_p[x]$
. Let
$Q_{i,p} \in{\mathbb{F}}_p[x]$
. Let
 $d_{i,p} \,:\!=\, \deg Q_{i,p}$
denote the degree of
$d_{i,p} \,:\!=\, \deg Q_{i,p}$
denote the degree of
 $Q_{i,p}$
. Then, the measure
$Q_{i,p}$
. Then, the measure
 $\mu _{p^m,Q}$
is given by the following identity:
$\mu _{p^m,Q}$
is given by the following identity:
 \begin{align*} \mu _{p^m,Q}\bigl (N_{p^m,Q}\bigr ) ={}&{} \frac{1}{\#N_{p^m,Q} \#{\operatorname{Aut}}_{R_{p^m,Q}}(N_{p^m,Q}) }\prod _{i = 1}^{r_p}\prod _{j=1}^\infty \\ &\ \times \left(1-\frac{\#\operatorname{Ext}_{R_{p^m,Q}}^1\bigl (N_{p^m,Q},{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x]) \bigr )}{\#{\operatorname{Hom}}_{R_{p^m,Q}}(N_{p^m,Q},{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x])} p^{-(1+j)d_{i,p} } \right). \end{align*}
\begin{align*} \mu _{p^m,Q}\bigl (N_{p^m,Q}\bigr ) ={}&{} \frac{1}{\#N_{p^m,Q} \#{\operatorname{Aut}}_{R_{p^m,Q}}(N_{p^m,Q}) }\prod _{i = 1}^{r_p}\prod _{j=1}^\infty \\ &\ \times \left(1-\frac{\#\operatorname{Ext}_{R_{p^m,Q}}^1\bigl (N_{p^m,Q},{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x]) \bigr )}{\#{\operatorname{Hom}}_{R_{p^m,Q}}(N_{p^m,Q},{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x])} p^{-(1+j)d_{i,p} } \right). \end{align*}
So far as it pertains to the group structure, the conclusion of Theorem 1.3 with
![]() $\mathscr{P} = \{p \}$
is weaker than Theorem 1.2, but only slightly. To study
$\mathscr{P} = \{p \}$
is weaker than Theorem 1.2, but only slightly. To study
![]() $\textrm{coker}({\mathbf{W}})_{p^m}$
itself, without the additional quotient by
$\textrm{coker}({\mathbf{W}})_{p^m}$
itself, without the additional quotient by
![]() $Q(x)$
, it would, namely, be sufficient to have a tightness condition stating that
$Q(x)$
, it would, namely, be sufficient to have a tightness condition stating that
![]() $ \lim _{C\to \infty } \liminf _{n\to \infty }{\mathbb{P}}(\# \textrm{coker}({\mathbf{W}})_{p^m} \leq C) = 1.$
Such a condition would yield the limiting law as a
$ \lim _{C\to \infty } \liminf _{n\to \infty }{\mathbb{P}}(\# \textrm{coker}({\mathbf{W}})_{p^m} \leq C) = 1.$
Such a condition would yield the limiting law as a
![]() ${\mathbb{Z}}[x]$
-module,Footnote 2 and the limiting law as a group then follows by summing over all
${\mathbb{Z}}[x]$
-module,Footnote 2 and the limiting law as a group then follows by summing over all
![]() ${\mathbb{Z}}[x]$
-module structures on
${\mathbb{Z}}[x]$
-module structures on
![]() $\oplus _{i=1}^\ell{\mathbb{Z}}/p^{\lambda _i}{\mathbb{Z}}$
.
$\oplus _{i=1}^\ell{\mathbb{Z}}/p^{\lambda _i}{\mathbb{Z}}$
.
We are not aware of a direct proof that the aforementioned sum recovers the formula in Theorem 1.2, but this would follow indirectly since Theorem 1.3 also applies to a matrix with uniform entries as in Theorem 1.2. So, if the tightness condition holds, then the distribution of
![]() $\textrm{coker}({\mathbf{W}})_{p^m}$
converges to the same limit as in Theorem 1.2, and one has asymptotic independence for any fixed finite set of primes. Hence, additionally assuming that the restriction to finite sets of primes can also be removed, we are led to the following:
$\textrm{coker}({\mathbf{W}})_{p^m}$
converges to the same limit as in Theorem 1.2, and one has asymptotic independence for any fixed finite set of primes. Hence, additionally assuming that the restriction to finite sets of primes can also be removed, we are led to the following:
Conjecture 1.4.
For every
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $\mathbf{X}$
be a
$\mathbf{X}$
be a
![]() $\{0,1 \}^{n\times n}$
-valued random matrix with independent entries, and let
$\{0,1 \}^{n\times n}$
-valued random matrix with independent entries, and let
![]() $b = e$
be the all-ones vector. Assume that there exists a sequence
$b = e$
be the all-ones vector. Assume that there exists a sequence
![]() $\alpha _n$
satisfying
$\alpha _n$
satisfying
![]() $\lim _{n\to \infty } n\alpha _n/\ln (n) = \infty$
such that
$\lim _{n\to \infty } n\alpha _n/\ln (n) = \infty$
such that
![]() ${\mathbb{P}}({\mathbf{X}}_{i,j} = 0),{\mathbb{P}}({\mathbf{X}}_{i,j} =1)\leq 1 -\alpha _n$
for each entry. Then,
${\mathbb{P}}({\mathbf{X}}_{i,j} = 0),{\mathbb{P}}({\mathbf{X}}_{i,j} =1)\leq 1 -\alpha _n$
for each entry. Then,
 \begin{align*} \lim _{n\to \infty }{}&{}{\mathbb{P}}\bigl ({\operatorname{coker}}({\mathbf{W}})_{p^2} \in \{0,{\mathbb{Z}}/p{\mathbb{Z}} \}\text{ for every odd prime p}\bigr )= \prod _{\text{odd primes }p} \big(1+p^{-1}\big) \prod _{i=0}^{\infty } \big(1-p^{-(i+1)}\big). \end{align*}
\begin{align*} \lim _{n\to \infty }{}&{}{\mathbb{P}}\bigl ({\operatorname{coker}}({\mathbf{W}})_{p^2} \in \{0,{\mathbb{Z}}/p{\mathbb{Z}} \}\text{ for every odd prime p}\bigr )= \prod _{\text{odd primes }p} \big(1+p^{-1}\big) \prod _{i=0}^{\infty } \big(1-p^{-(i+1)}\big). \end{align*}
Remark 1.5. The restriction that
![]() $\alpha _n \gg \ln (n)/n$
in Theorem 1.3, which limits how sparse the matrices are allowed to be, is close to optimal. The conclusion of Theorem 1.3, namely, has to fail when
$\alpha _n \gg \ln (n)/n$
in Theorem 1.3, which limits how sparse the matrices are allowed to be, is close to optimal. The conclusion of Theorem 1.3, namely, has to fail when
![]() $\mathbf{X}$
has independent entries satisfying
$\mathbf{X}$
has independent entries satisfying
![]() ${\mathbb{P}}({\mathbf{X}}_{i,j} = 0) \geq 1 - (1-\varepsilon )\ln (n)/n$
for
${\mathbb{P}}({\mathbf{X}}_{i,j} = 0) \geq 1 - (1-\varepsilon )\ln (n)/n$
for
![]() $\varepsilon \gt 0$
.
$\varepsilon \gt 0$
.
Indeed, the coupon collector theorem then implies that
![]() $\mathbf{X}$
has many rows equal to zero so that
$\mathbf{X}$
has many rows equal to zero so that
![]() ${\textrm{rank}}({\mathbf{X}}) \leq n-2$
with high probability. The latter implies that
${\textrm{rank}}({\mathbf{X}}) \leq n-2$
with high probability. The latter implies that
![]() ${\mathbf{X}}({\mathbb{F}}_p^n) +{\mathbb{F}}_p b \neq{\mathbb{F}}_p^n$
. Hence, since
${\mathbf{X}}({\mathbb{F}}_p^n) +{\mathbb{F}}_p b \neq{\mathbb{F}}_p^n$
. Hence, since
![]() $\textrm{coker}({\mathbf{W}})_{p,x} \cong{\mathbb{Z}}^n/({\mathbf{W}}({\mathbb{Z}}^n) + p{\mathbb{Z}}^n + x{\mathbb{Z}}^n)$
is isomorphic to
$\textrm{coker}({\mathbf{W}})_{p,x} \cong{\mathbb{Z}}^n/({\mathbf{W}}({\mathbb{Z}}^n) + p{\mathbb{Z}}^n + x{\mathbb{Z}}^n)$
is isomorphic to
![]() ${\mathbb{F}}_p^n/({\mathbf{X}}({\mathbb{F}}_p^n) +{\mathbb{F}}_p b)$
, it would follow that
${\mathbb{F}}_p^n/({\mathbf{X}}({\mathbb{F}}_p^n) +{\mathbb{F}}_p b)$
, it would follow that
![]() $\lim _{n\to \infty }{\mathbb{P}}(\textrm{coker}({\mathbf{W}})_{p,x} = \{0 \}) = 0$
. This is incompatible with the conclusion of Theorem 1.3 since
$\lim _{n\to \infty }{\mathbb{P}}(\textrm{coker}({\mathbf{W}})_{p,x} = \{0 \}) = 0$
. This is incompatible with the conclusion of Theorem 1.3 since
![]() $\mu _{p,x}(\{0\}) = \prod _{j=1}^\infty (1-p^{-1 - j}) \neq 0$
.
$\mu _{p,x}(\{0\}) = \prod _{j=1}^\infty (1-p^{-1 - j}) \neq 0$
.
Remark 1.6. The limiting distribution of the
![]() ${\mathbb{Z}}[x]$
-module
${\mathbb{Z}}[x]$
-module
![]() $\textrm{coker}(Q({\mathbf{X}}))$
with
$\textrm{coker}(Q({\mathbf{X}}))$
with
![]() $Q(x)$
a fixed polynomial was recently studied by Cheong and Yu [Reference Cheong and Yu3]. Interestingly, the formulas found in Theorem 1.3 and [3, Theorem 1.3] bear a close resemblance, although they are not identical. This resemblance is not entirely surprising since the studied objects can be related. Indeed, note that
$Q(x)$
a fixed polynomial was recently studied by Cheong and Yu [Reference Cheong and Yu3]. Interestingly, the formulas found in Theorem 1.3 and [3, Theorem 1.3] bear a close resemblance, although they are not identical. This resemblance is not entirely surprising since the studied objects can be related. Indeed, note that
![]() $\textrm{coker}(Q({\mathbf{X}}))_{p^m} \cong{\mathbb{Z}}^n / (Q(x){\mathbb{Z}}^n + p^m{\mathbb{Z}}^n)$
whereas
$\textrm{coker}(Q({\mathbf{X}}))_{p^m} \cong{\mathbb{Z}}^n / (Q(x){\mathbb{Z}}^n + p^m{\mathbb{Z}}^n)$
whereas
![]() $\textrm{coker}({\mathbf{W}})_{p^m,Q}\cong{\mathbb{Z}}^n/(Q(x){\mathbb{Z}}^n + p^m{\mathbb{Z}}^n +{\mathbb{Z}}[x]b)$
.
$\textrm{coker}({\mathbf{W}})_{p^m,Q}\cong{\mathbb{Z}}^n/(Q(x){\mathbb{Z}}^n + p^m{\mathbb{Z}}^n +{\mathbb{Z}}[x]b)$
.
One can however not directly recover Theorem 1.3 from [3]. For one thing, [3] only considers the case
![]() $\mathscr{P} = \{p\}$
and does not allow sparse settings where
$\mathscr{P} = \{p\}$
and does not allow sparse settings where
![]() $\alpha _n \to 0$
. Further,
$\alpha _n \to 0$
. Further,
![]() $\textrm{coker}({\mathbf{W}})_{p^m, Q}$
not only depends on the isomorphism class of
$\textrm{coker}({\mathbf{W}})_{p^m, Q}$
not only depends on the isomorphism class of
![]() $\textrm{coker}(Q({\mathbf{X}}))_{p^m}$
but also on how the reduction of
$\textrm{coker}(Q({\mathbf{X}}))_{p^m}$
but also on how the reduction of
![]() $b$
lies in
$b$
lies in
![]() $\textrm{coker}(Q({\mathbf{X}}))_{p^m}$
, which is information we do not have access to.
$\textrm{coker}(Q({\mathbf{X}}))_{p^m}$
, which is information we do not have access to.
1.2 Proof techniques
The proof of Theorem 1.2 relies on an analysis of the sequence of random vectors
![]() $({\mathbf{X}}^{t-1}b)_{t=1}^n$
, viewed as a stochastic process. More precisely, we show in Corollary 2.2 that the group structure of
$({\mathbf{X}}^{t-1}b)_{t=1}^n$
, viewed as a stochastic process. More precisely, we show in Corollary 2.2 that the group structure of
![]() $\textrm{coker}({\mathbf{W}})_{p^m}$
can be computed in terms of the sequence of random variables
$\textrm{coker}({\mathbf{W}})_{p^m}$
can be computed in terms of the sequence of random variables
![]() $0 = U_1 \leq U_2 \leq \ldots \leq U_n \leq \infty$
defined by
$0 = U_1 \leq U_2 \leq \ldots \leq U_n \leq \infty$
defined by
Here, given a ring
![]() $R$
and
$R$
and
![]() $v_1,\ldots, v_t \in R^n$
, we write
$v_1,\ldots, v_t \in R^n$
, we write
![]() $\textrm{span}_{R}(v_1,\ldots, v_t) \,:\!=\, \big\{\sum _{i=1}^t c_i v_i\,:\, c_i \in R \big\}$
. The remaining difficulty is then to study the joint law of the
$\textrm{span}_{R}(v_1,\ldots, v_t) \,:\!=\, \big\{\sum _{i=1}^t c_i v_i\,:\, c_i \in R \big\}$
. The remaining difficulty is then to study the joint law of the
![]() $U_j$
. The distributional assumption in Theorem 1.2 plays an important role for the latter task: the independence and equidistribution of the entries imply that
$U_j$
. The distributional assumption in Theorem 1.2 plays an important role for the latter task: the independence and equidistribution of the entries imply that
![]() $\mathbf{X}$
induces a uniform random endomorphism of
$\mathbf{X}$
induces a uniform random endomorphism of
![]() $({\mathbb{Z}}/p^m{\mathbb{Z}})^n$
, which can be used to establish Markovian dynamics for
$({\mathbb{Z}}/p^m{\mathbb{Z}})^n$
, which can be used to establish Markovian dynamics for
![]() $\min \{U_t, m\}$
; see Lemma 2.4.
$\min \{U_t, m\}$
; see Lemma 2.4.
This proof yields a direct combinatorial interpretation for the formula in Theorem 1.2. Given
![]() $U_t$
, a counting argument implies that the probability that
$U_t$
, a counting argument implies that the probability that
![]() $U_{t+1} \geq U_t + \delta$
is
$U_{t+1} \geq U_t + \delta$
is
![]() $p^{-\delta (n-t)}$
for any
$p^{-\delta (n-t)}$
for any
![]() $\delta$
satisfying
$\delta$
satisfying
![]() $U_t + \delta \leq m$
. Taking
$U_t + \delta \leq m$
. Taking
![]() $j=n-t$
then explains the factors of the form
$j=n-t$
then explains the factors of the form
![]() $p^{-j\delta _j}$
in Theorem 1.2. Factors of the form
$p^{-j\delta _j}$
in Theorem 1.2. Factors of the form
![]() $1-p^{-j}$
arise when we additionally have to enforce that
$1-p^{-j}$
arise when we additionally have to enforce that
![]() $U_{t+1} \leq U_t + \delta$
. A further benefit of the approach is that it can also be used to establish the law of
$U_{t+1} \leq U_t + \delta$
. A further benefit of the approach is that it can also be used to establish the law of
![]() $\textrm{coker}({\mathbf{W}})_{p^m}$
for finite
$\textrm{coker}({\mathbf{W}})_{p^m}$
for finite
![]() $n$
; see Proposition 2.5.
$n$
; see Proposition 2.5.
The proof of Theorem 1.3 relies on more sophisticated techniques. In particular, we employ the category-theoretic moment method. In classical probability theory, the moment method allows one to establish convergence in distribution of a sequence of
![]() $\mathbb{R}$
-valued random variables
$\mathbb{R}$
-valued random variables
![]() $(Y_i)_{i=1}^\infty$
by showing that the moments
$(Y_i)_{i=1}^\infty$
by showing that the moments
![]() ${\mathbb{E}}[Y_i^n]$
converge to those of the desired limiting law provided that some mild conditions are satisfied. Results of Sawin and Wood [Reference Sawin and Wood20] similarly allow one to establish limiting laws for random algebraic objects such as groups and modules by showing that category-theoretic moments converge. Here, given a ring
${\mathbb{E}}[Y_i^n]$
converge to those of the desired limiting law provided that some mild conditions are satisfied. Results of Sawin and Wood [Reference Sawin and Wood20] similarly allow one to establish limiting laws for random algebraic objects such as groups and modules by showing that category-theoretic moments converge. Here, given a ring
![]() $R$
and a deterministic
$R$
and a deterministic
![]() $R$
-module
$R$
-module
![]() $N$
, the
$N$
, the
![]() $N$
-moment
Footnote
3
of a random
$N$
-moment
Footnote
3
of a random
![]() $R$
-module
$R$
-module
![]() $Y$
is given by
$Y$
is given by
![]() ${\mathbb{E}}[\#\textrm{Sur}_{R}(Y,N)]$
where
${\mathbb{E}}[\#\textrm{Sur}_{R}(Y,N)]$
where
![]() $\textrm{Sur}_R(Y,N)$
denotes the set of surjective
$\textrm{Sur}_R(Y,N)$
denotes the set of surjective
![]() $R$
-module morphisms from
$R$
-module morphisms from
![]() $Y$
to
$Y$
to
![]() $N$
.
$N$
.
The main challenge is hence to estimate the
![]() $N$
-moments of the random
$N$
-moments of the random
![]() ${\mathbb{Z}}[x]$
-module
${\mathbb{Z}}[x]$
-module
![]() $\textrm{coker}({\mathbf{W}})$
. To this end, we employ a strategy developed by Wood [Reference Wood32, Reference Wood33] and Nguyen and Wood [Reference Nguyen and Wood15] for the estimation of moments of random algebraic objects associated with random matrices with
$\textrm{coker}({\mathbf{W}})$
. To this end, we employ a strategy developed by Wood [Reference Wood32, Reference Wood33] and Nguyen and Wood [Reference Nguyen and Wood15] for the estimation of moments of random algebraic objects associated with random matrices with
![]() $\alpha$
-balanced entries. A key difference between our setting and the one in [Reference Nguyen and Wood15, Reference Wood32, Reference Wood33] is that we have little control over the joint law of the entries
$\alpha$
-balanced entries. A key difference between our setting and the one in [Reference Nguyen and Wood15, Reference Wood32, Reference Wood33] is that we have little control over the joint law of the entries
![]() ${\mathbf{W}}_{i,j}$
of our matrix of interest since these are nontrivial algebraic combinations of the entries of
${\mathbf{W}}_{i,j}$
of our matrix of interest since these are nontrivial algebraic combinations of the entries of
![]() $\mathbf{X}$
. This is why it is essential to view
$\mathbf{X}$
. This is why it is essential to view
![]() $\textrm{coker}({\mathbf{W}})$
as a
$\textrm{coker}({\mathbf{W}})$
as a
![]() ${\mathbb{Z}}[x]$
-module, not only as a group. That is, the
${\mathbb{Z}}[x]$
-module, not only as a group. That is, the
![]() ${\mathbb{Z}}[x]$
-module-theoretic viewpoint allows us to untangle the algebraic dependencies and hence estimate the category-theoretic moments; see (3.3) and the subsequent remarks.
${\mathbb{Z}}[x]$
-module-theoretic viewpoint allows us to untangle the algebraic dependencies and hence estimate the category-theoretic moments; see (3.3) and the subsequent remarks.
The advantage of the category-theoretic approach is that it is robust, as is demonstrated by the general distributional assumptions in Theorem 1.3. For comparison, the proof approach for Theorem 1.2 is highly non-robust. Indeed, as mentioned above, that proof uses that
![]() $\mathbf{X}$
induces a uniform random endomorphism of
$\mathbf{X}$
induces a uniform random endomorphism of
![]() $({\mathbb{Z}}/p^m{\mathbb{Z}})^n$
: a property which is only satisfied when
$({\mathbb{Z}}/p^m{\mathbb{Z}})^n$
: a property which is only satisfied when
![]() ${\mathbf{X}} \bmod p^m$
has independent and uniformly distributed entries. The robustness of the category-theoretic approach makes us hopeful that we will be able to generalise it in future work, although this remains a nontrivial task; see Section 4.
${\mathbf{X}} \bmod p^m$
has independent and uniformly distributed entries. The robustness of the category-theoretic approach makes us hopeful that we will be able to generalise it in future work, although this remains a nontrivial task; see Section 4.
2. Proof of Theorem 1.2
Throughout this section, we fix a prime
![]() $p$
and a vector
$p$
and a vector
![]() $b\in{\mathbb{Z}}^n$
with
$b\in{\mathbb{Z}}^n$
with
![]() $b\not \equiv 0 \bmod p$
. Recall from Section 1.2 that the proof has two main ingredients. The first ingredient is Corollary 2.2, which shows that the group structure of
$b\not \equiv 0 \bmod p$
. Recall from Section 1.2 that the proof has two main ingredients. The first ingredient is Corollary 2.2, which shows that the group structure of
![]() $\textrm{coker}({\mathbf{W}})_{p^m}$
can be computed in terms of
$\textrm{coker}({\mathbf{W}})_{p^m}$
can be computed in terms of
![]() $U_1,\ldots, U_n$
. The second ingredient is Lemma 2.4, which concerns the joint law of the
$U_1,\ldots, U_n$
. The second ingredient is Lemma 2.4, which concerns the joint law of the
![]() $U_t$
when
$U_t$
when
![]() $\mathbf{X}$
is random as in Theorem 1.2. We combine these results to establish Theorem 1.2 in Section 2.3.
$\mathbf{X}$
is random as in Theorem 1.2. We combine these results to establish Theorem 1.2 in Section 2.3.
2.1
Computing
 $\textrm{coker}({\mathbf{W}})_{p^m}$
in terms of
$\textrm{coker}({\mathbf{W}})_{p^m}$
in terms of
 $U_1,\ldots, U_n$
$U_1,\ldots, U_n$
Recall the definition of
![]() $U_t$
from (1.1). Fix an integer
$U_t$
from (1.1). Fix an integer
![]() $m\geq 1$
and abbreviate
$m\geq 1$
and abbreviate
![]() $R \,:\!=\,{\mathbb{Z}}/p^m{\mathbb{Z}}$
. The following lemma then produces an
$R \,:\!=\,{\mathbb{Z}}/p^m{\mathbb{Z}}$
. The following lemma then produces an
![]() $R$
-module basis for
$R$
-module basis for
![]() $R^n$
which is well-adapted to the computation of
$R^n$
which is well-adapted to the computation of
![]() $\textrm{coker}({\mathbf{W}})_{p^m}$
.
$\textrm{coker}({\mathbf{W}})_{p^m}$
.
Lemma 2.1.
Write
![]() $\Lambda _t \,:\!=\, \min \{U_t,m \}$
. Then, there exist
$\Lambda _t \,:\!=\, \min \{U_t,m \}$
. Then, there exist
![]() $v_1,\ldots, v_n \in R^n$
such that for every
$v_1,\ldots, v_n \in R^n$
such that for every
![]() $t \leq n$
the following properties are satisfied:
$t \leq n$
the following properties are satisfied:
-
(i) The reduction of the matrix
 $(v_1,\ldots, v_t)$
modulo
$(v_1,\ldots, v_t)$
modulo
 $p$
has rank
$p$
has rank
 $t$
over
$t$
over
 ${\mathbb{F}}_p$
.
${\mathbb{F}}_p$
. -
(ii) It holds that
 $\operatorname{span}_{R}\big({\mathbf{X}}^{i-1} b \bmod p^m\,:\,1\leq i\leq t\big) = \operatorname{span}_{R}\big(p^{\Lambda _i}v_i\,:\, 1 \leq i\leq t\big)$
.
$\operatorname{span}_{R}\big({\mathbf{X}}^{i-1} b \bmod p^m\,:\,1\leq i\leq t\big) = \operatorname{span}_{R}\big(p^{\Lambda _i}v_i\,:\, 1 \leq i\leq t\big)$
.
Proof. We proceed by induction on
![]() $t$
. If
$t$
. If
![]() $t = 1$
, then
$t = 1$
, then
![]() $U_1 = 0$
, so
$U_1 = 0$
, so
![]() $v_1 \equiv b \bmod p^m$
satisfies both properties. Now suppose that
$v_1 \equiv b \bmod p^m$
satisfies both properties. Now suppose that
![]() $t\gt 1$
and assume that there exist
$t\gt 1$
and assume that there exist
![]() $v_1,\ldots, v_{t-1}$
such that both properties are satisfied. We prove the existence of some
$v_1,\ldots, v_{t-1}$
such that both properties are satisfied. We prove the existence of some
![]() $v_{t}$
.
$v_{t}$
.
First, suppose that
![]() $U_{t} \geq m$
. Then, the definition (1.1) yields
$U_{t} \geq m$
. Then, the definition (1.1) yields
![]() $\textrm{span}_{R}\big({\mathbf{X}}^{i-1} b \bmod p^m\,:\,i\leq t\big) = \textrm{span}_{R}\big({\mathbf{X}}^{i-1} b \bmod p^m\,:\,i\leq t-1\big)$
and
$\textrm{span}_{R}\big({\mathbf{X}}^{i-1} b \bmod p^m\,:\,i\leq t\big) = \textrm{span}_{R}\big({\mathbf{X}}^{i-1} b \bmod p^m\,:\,i\leq t-1\big)$
and
![]() $p^{\Lambda _{t}}v = p^{m}v = 0$
for every
$p^{\Lambda _{t}}v = p^{m}v = 0$
for every
![]() $v\in R^n$
. Consequently, due to the induction hypothesis, both properties are satisfied if we let
$v\in R^n$
. Consequently, due to the induction hypothesis, both properties are satisfied if we let
![]() $v_{t}\in R^n$
be an arbitrary vector, which is not in
$v_{t}\in R^n$
be an arbitrary vector, which is not in
![]() $\textrm{span}_{R}(v_1,\ldots, v_{t-1}) + pR^n$
. Such a vector exists because
$\textrm{span}_{R}(v_1,\ldots, v_{t-1}) + pR^n$
. Such a vector exists because
![]() $t -1 \lt n$
.
$t -1 \lt n$
.
Now suppose that
![]() $U_{t} \lt m$
. By definition of
$U_{t} \lt m$
. By definition of
![]() $U_{t}$
, there then exist
$U_{t}$
, there then exist
![]() $w \in p^{U_{t}}R^n$
and
$w \in p^{U_{t}}R^n$
and
![]() $r \in \textrm{span}_{R}\big({\mathbf{X}}^{i-1}b\bmod p^m\,:\, i\leq t-1\big)$
such that
$r \in \textrm{span}_{R}\big({\mathbf{X}}^{i-1}b\bmod p^m\,:\, i\leq t-1\big)$
such that
![]() ${\mathbf{X}}^{t-1}b \equiv w + r \bmod p^m$
. Pick some
${\mathbf{X}}^{t-1}b \equiv w + r \bmod p^m$
. Pick some
![]() $v_{t}\in R^n$
with
$v_{t}\in R^n$
with
![]() $p^{U_{t}}v_{t}= w$
. Then, due to the induction hypothesis, item (ii) is satisfied, and item (i) is equivalent to the statement that
$p^{U_{t}}v_{t}= w$
. Then, due to the induction hypothesis, item (ii) is satisfied, and item (i) is equivalent to the statement that
![]() $v_{t} \not \in \textrm{span}_R(v_1,\ldots, v_{t-1}) + pR^n$
. The latter statement is true. Indeed, if not, then
$v_{t} \not \in \textrm{span}_R(v_1,\ldots, v_{t-1}) + pR^n$
. The latter statement is true. Indeed, if not, then
![]() $w \in \textrm{span}_R\big(p^{U_{t}}v_1,\ldots, p^{U_{t}}v_{t-1}\big) + p^{U_{t} + 1}R^n$
. Then, considering that
$w \in \textrm{span}_R\big(p^{U_{t}}v_1,\ldots, p^{U_{t}}v_{t-1}\big) + p^{U_{t} + 1}R^n$
. Then, considering that
![]() $\textrm{span}_R(p^{U_{t}}v_i\,:\, i\leq t-1) \subseteq \textrm{span}_R({\mathbf{X}}^{i-1}b \bmod p^m\,:\,i\leq t-1)$
by item (ii) of the induction hypothesis and the fact that the
$\textrm{span}_R(p^{U_{t}}v_i\,:\, i\leq t-1) \subseteq \textrm{span}_R({\mathbf{X}}^{i-1}b \bmod p^m\,:\,i\leq t-1)$
by item (ii) of the induction hypothesis and the fact that the
![]() $U_i$
are nondecreasing, it follows from
$U_i$
are nondecreasing, it follows from
![]() ${\mathbf{X}}^{t-1}b \equiv w + r \bmod p^m$
that
${\mathbf{X}}^{t-1}b \equiv w + r \bmod p^m$
that
![]() ${\mathbf{X}}^{t-1}b \in \textrm{span}_{\mathbb{Z}}({\mathbf{X}}^{i-1}b \,:\,i\leq t-1) + p^{U_{t}+1}{\mathbb{Z}}^n$
contradicting the maximality of
${\mathbf{X}}^{t-1}b \in \textrm{span}_{\mathbb{Z}}({\mathbf{X}}^{i-1}b \,:\,i\leq t-1) + p^{U_{t}+1}{\mathbb{Z}}^n$
contradicting the maximality of
![]() $U_{t}$
in (1.1). This shows that both properties are satisfied.
$U_{t}$
in (1.1). This shows that both properties are satisfied.
Corollary 2.2.
Adopt the notation of Lemma 2.1
. Then,
![]() ${\operatorname{coker}}({\mathbf{W}})_{p^m} \cong \oplus _{t=1}^n{\mathbb{Z}}/p^{\Lambda _t}{\mathbb{Z}}$
.
${\operatorname{coker}}({\mathbf{W}})_{p^m} \cong \oplus _{t=1}^n{\mathbb{Z}}/p^{\Lambda _t}{\mathbb{Z}}$
.
Proof. The case with
![]() $t=n$
in item (i) of Lemma 2.1 implies that the vectors
$t=n$
in item (i) of Lemma 2.1 implies that the vectors
![]() $v_1,\ldots, v_n \in R^n$
determine an
$v_1,\ldots, v_n \in R^n$
determine an
![]() $R$
-module basis for
$R$
-module basis for
![]() $R^n$
. Further, item (ii) yields that
$R^n$
. Further, item (ii) yields that
![]() ${\mathbf{W}}(R^n) = \textrm{span}_{R}\big(p^{\Lambda _1}v_1,\ldots, p^{\Lambda _n}v_n\big)$
. The claim is hence immediate since
${\mathbf{W}}(R^n) = \textrm{span}_{R}\big(p^{\Lambda _1}v_1,\ldots, p^{\Lambda _n}v_n\big)$
. The claim is hence immediate since
![]() $\textrm{coker}({\mathbf{W}})_{p^m} \cong R^n/{\mathbf{W}}(R^n)$
.
$\textrm{coker}({\mathbf{W}})_{p^m} \cong R^n/{\mathbf{W}}(R^n)$
.
2.2 Markovian dynamics
Given a matrix
![]() $\mathbf{M}$
, abbreviate
$\mathbf{M}$
, abbreviate
![]() ${\textrm{rank}}_p({\mathbf{M}})$
for the rank of
${\textrm{rank}}_p({\mathbf{M}})$
for the rank of
![]() ${\mathbf{M}} \bmod p$
over
${\mathbf{M}} \bmod p$
over
![]() ${\mathbb{F}}_p$
. Recall that
${\mathbb{F}}_p$
. Recall that
![]() $R ={\mathbb{Z}}/p^m{\mathbb{Z}}$
. The following lemma provides a partial converse for Lemma 2.1 in the case
$R ={\mathbb{Z}}/p^m{\mathbb{Z}}$
. The following lemma provides a partial converse for Lemma 2.1 in the case
![]() $U_t\lt m$
:
$U_t\lt m$
:
Lemma 2.3.
Consider some
![]() $t\leq n$
and integers
$t\leq n$
and integers
![]() $0 = u_1\leq u_2 \leq \ldots \leq u_t \lt m$
. Then, it holds that
$0 = u_1\leq u_2 \leq \ldots \leq u_t \lt m$
. Then, it holds that
![]() $U_i = u_i$
for every
$U_i = u_i$
for every
![]() $i\leq t$
if and only if there exist
$i\leq t$
if and only if there exist
![]() $v_1,\ldots, v_t \in R^n$
with
$v_1,\ldots, v_t \in R^n$
with
![]() ${\operatorname{rank}}_p(v_1,\ldots, v_t) = t$
such that for every
${\operatorname{rank}}_p(v_1,\ldots, v_t) = t$
such that for every
![]() $i\leq t$
one has
$i\leq t$
one has
![]() $\operatorname{span}_{R}({\mathbf{X}}^{j-1} b \bmod p^m\,:\,j\leq i) =\operatorname{span}_{R}(p^{u_j}v_j\,:\, j\leq i)$
.
$\operatorname{span}_{R}({\mathbf{X}}^{j-1} b \bmod p^m\,:\,j\leq i) =\operatorname{span}_{R}(p^{u_j}v_j\,:\, j\leq i)$
.
Proof. If
![]() $U_i = u_i$
for every
$U_i = u_i$
for every
![]() $i\leq t$
, then the existence of
$i\leq t$
, then the existence of
![]() $v_1,\ldots, v_t$
with the claimed properties follows from Lemma 2.1. Conversely, assume that such
$v_1,\ldots, v_t$
with the claimed properties follows from Lemma 2.1. Conversely, assume that such
![]() $v_1,\ldots, v_t$
exist. Then, for every
$v_1,\ldots, v_t$
exist. Then, for every
![]() $i\leq t$
,
$i\leq t$
,
 \begin{align} \textrm{span}_R\big({\mathbf{X}}^{j-1}b \bmod p^m\,:\, j\leq i\big) &= \textrm{span}_R\big(p^{u_j}v_j\,:\,j\lt i\big) + \textrm{span}_R(p^{u_i}v_i) \\ &\subseteq \textrm{span}_R\big({\mathbf{X}}^{j-1}b \bmod p^m\,:\, j\lt i\big) + p^{u_i}R^n.\nonumber \end{align}
\begin{align} \textrm{span}_R\big({\mathbf{X}}^{j-1}b \bmod p^m\,:\, j\leq i\big) &= \textrm{span}_R\big(p^{u_j}v_j\,:\,j\lt i\big) + \textrm{span}_R(p^{u_i}v_i) \\ &\subseteq \textrm{span}_R\big({\mathbf{X}}^{j-1}b \bmod p^m\,:\, j\lt i\big) + p^{u_i}R^n.\nonumber \end{align}
Considering that
![]() $R ={\mathbb{Z}}/p^m{\mathbb{Z}}$
with
$R ={\mathbb{Z}}/p^m{\mathbb{Z}}$
with
![]() $m \geq u_i$
, it follows that
$m \geq u_i$
, it follows that
![]() ${\mathbf{X}}^{i-1}b \in \textrm{span}_{\mathbb{Z}}({\mathbf{X}}^{j-1}b\,:\, j\lt i) + p^{u_i}{\mathbb{Z}}^n$
. The definition (1.1) hence yields
${\mathbf{X}}^{i-1}b \in \textrm{span}_{\mathbb{Z}}({\mathbf{X}}^{j-1}b\,:\, j\lt i) + p^{u_i}{\mathbb{Z}}^n$
. The definition (1.1) hence yields
![]() $U_i \geq u_i$
. On the other hand, since
$U_i \geq u_i$
. On the other hand, since
![]() ${\textrm{rank}}_p(v_1,\ldots, v_t) = t$
and
${\textrm{rank}}_p(v_1,\ldots, v_t) = t$
and
![]() $u_i \lt m$
, we have
$u_i \lt m$
, we have
![]() $p^{u_i}v_i \not \in \textrm{span}_R(p^{u_j}v_j\,:\,j \lt i) + p^{u_i + 1}R^n$
. Hence,
$p^{u_i}v_i \not \in \textrm{span}_R(p^{u_j}v_j\,:\,j \lt i) + p^{u_i + 1}R^n$
. Hence,
 \begin{align} \textrm{span}_R\big(p^{u_j}v_j\,:\,j\lt i\big) + \textrm{span}_R(p^{u_i}v_i) &\not \subseteq \textrm{span}_R\big(p^{u_j}v_j\,:\,j\lt i\big) + p^{u_i + 1}R^n\\ &= \textrm{span}_R\big({\mathbf{X}}^{j-1}b \bmod p^m\,:\, j\lt i\big) + p^{u_i + 1}R^n.\nonumber \end{align}
\begin{align} \textrm{span}_R\big(p^{u_j}v_j\,:\,j\lt i\big) + \textrm{span}_R(p^{u_i}v_i) &\not \subseteq \textrm{span}_R\big(p^{u_j}v_j\,:\,j\lt i\big) + p^{u_i + 1}R^n\\ &= \textrm{span}_R\big({\mathbf{X}}^{j-1}b \bmod p^m\,:\, j\lt i\big) + p^{u_i + 1}R^n.\nonumber \end{align}
Given the equality in (2.1) and the fact that
![]() $u_i+1 \leq m$
, this implies that
$u_i+1 \leq m$
, this implies that
![]() ${\mathbf{X}}^{i-1}b \not \in \textrm{span}_{{\mathbb{Z}}}({\mathbf{X}}^{j-1}b\,:\,j\lt i) + p^{u_i+1}{\mathbb{Z}}^n$
. This means that
${\mathbf{X}}^{i-1}b \not \in \textrm{span}_{{\mathbb{Z}}}({\mathbf{X}}^{j-1}b\,:\,j\lt i) + p^{u_i+1}{\mathbb{Z}}^n$
. This means that
![]() $U_i\leq u_i$
. Combine the inequalities
$U_i\leq u_i$
. Combine the inequalities
![]() $U_i \geq u_i$
and
$U_i \geq u_i$
and
![]() $U_i \leq u_i$
to conclude the proof.
$U_i \leq u_i$
to conclude the proof.
Lemma 2.4.
Assume that
![]() $\mathbf{X}$
has independent and
$\mathbf{X}$
has independent and
![]() ${\operatorname{Unif}}\{0,1,\ldots, p^{m}-1 \}$
-distributed entries. Consider some
${\operatorname{Unif}}\{0,1,\ldots, p^{m}-1 \}$
-distributed entries. Consider some
![]() $t\leq n-1$
. Then, for every
$t\leq n-1$
. Then, for every
![]() $0= u_1\leq \ldots \leq u_t\lt m$
and
$0= u_1\leq \ldots \leq u_t\lt m$
and
![]() $u_{t+1} \leq m$
,
$u_{t+1} \leq m$
,
In particular, if additionally
![]() $u_{t+1} \lt m$
,
$u_{t+1} \lt m$
,
Proof. Two ordered sets of vectors
![]() $v_1,\ldots, v_t \in R^n$
and
$v_1,\ldots, v_t \in R^n$
and
![]() $w_1,\ldots, w_t\in R^n$
are said to be equivalent if
$w_1,\ldots, w_t\in R^n$
are said to be equivalent if
![]() $\textrm{span}_{R}(p^{u_j}v_j\,:\,j\leq i) = \textrm{span}_{R}(p^{u_j}w_j\,:\,j\leq i)$
for every
$\textrm{span}_{R}(p^{u_j}v_j\,:\,j\leq i) = \textrm{span}_{R}(p^{u_j}w_j\,:\,j\leq i)$
for every
![]() $i \leq t$
.
$i \leq t$
.
Lemma 2.3 implies that the event
![]() $\{U_i = u_i\,:\,\forall i\leq t \}$
can be written as a union of events of the form
$\{U_i = u_i\,:\,\forall i\leq t \}$
can be written as a union of events of the form
![]() $\{\textrm{span}_{R}({\mathbf{X}}^{j-1} b \bmod p^m\,:\,j\leq i) = \textrm{span}_{R}(p^{u_j}v_j\,:\,j\leq i),\, \forall i\leq t\}$
indexed by vectors
$\{\textrm{span}_{R}({\mathbf{X}}^{j-1} b \bmod p^m\,:\,j\leq i) = \textrm{span}_{R}(p^{u_j}v_j\,:\,j\leq i),\, \forall i\leq t\}$
indexed by vectors
![]() $v_1,\ldots, v_t\in R^n$
with
$v_1,\ldots, v_t\in R^n$
with
![]() ${\textrm{rank}}_p(v_1,\ldots, v_t) = t$
and
${\textrm{rank}}_p(v_1,\ldots, v_t) = t$
and
![]() $\textrm{span}_R(v_1) = \textrm{span}_R(b\bmod p^m)$
. Two such events are equal if the corresponding sets of vectors are equivalent and mutually exclusive otherwise. Hence, by conditioning on the equivalence class, (2.3) follows if we show that for every
$\textrm{span}_R(v_1) = \textrm{span}_R(b\bmod p^m)$
. Two such events are equal if the corresponding sets of vectors are equivalent and mutually exclusive otherwise. Hence, by conditioning on the equivalence class, (2.3) follows if we show that for every
![]() $v_1,\ldots, v_t \in R^n$
with
$v_1,\ldots, v_t \in R^n$
with
![]() ${\textrm{rank}}_p(v_1,\ldots, v_t) = t$
and
${\textrm{rank}}_p(v_1,\ldots, v_t) = t$
and
![]() $\textrm{span}_R(v_1) = \textrm{span}_R(b\bmod p^m)$
,
$\textrm{span}_R(v_1) = \textrm{span}_R(b\bmod p^m)$
,
Fix
![]() $v_1,\ldots, v_t$
and let
$v_1,\ldots, v_t$
and let
![]() $E\,:\!=\, \{\textrm{span}_R\big({\mathbf{X}}^{j-1}b \bmod p^m\,:\, j\leq i\big) = \textrm{span}_{R}(p^{u_j}v_j\,:\,j\leq i), \, \forall i\leq t\}$
denote the event in the condition of (2.5).
$E\,:\!=\, \{\textrm{span}_R\big({\mathbf{X}}^{j-1}b \bmod p^m\,:\, j\leq i\big) = \textrm{span}_{R}(p^{u_j}v_j\,:\,j\leq i), \, \forall i\leq t\}$
denote the event in the condition of (2.5).
It follows from the definition that
![]() $U_{t+1} \geq u_{t+1}$
if and only if
$U_{t+1} \geq u_{t+1}$
if and only if
![]() ${\mathbf{X}}(\textrm{span}_{\mathbb{Z}}({\mathbf{X}}^{i-1}b\,:\,i\leq t))\subseteq \textrm{span}_{\mathbb{Z}}({\mathbf{X}}^{i-1}b\,:\,i\leq t) + p^{u_{t+1}}{\mathbb{Z}}^n$
. Hence, conditional on
${\mathbf{X}}(\textrm{span}_{\mathbb{Z}}({\mathbf{X}}^{i-1}b\,:\,i\leq t))\subseteq \textrm{span}_{\mathbb{Z}}({\mathbf{X}}^{i-1}b\,:\,i\leq t) + p^{u_{t+1}}{\mathbb{Z}}^n$
. Hence, conditional on
![]() $E$
, one has
$E$
, one has
![]() $U_{t+1} \geq u_{t+1}$
if and only if
$U_{t+1} \geq u_{t+1}$
if and only if
![]() ${\mathbf{X}}(p^{u_t}v_t) \in \textrm{span}_R(p^{u_j}v_j\,:\, j\leq t) +p^{u_{t+1}}R^n$
. Considering that
${\mathbf{X}}(p^{u_t}v_t) \in \textrm{span}_R(p^{u_j}v_j\,:\, j\leq t) +p^{u_{t+1}}R^n$
. Considering that
![]() ${\textrm{rank}}_p(v_1,\ldots, v_t)=t$
and that the
${\textrm{rank}}_p(v_1,\ldots, v_t)=t$
and that the
![]() $u_i$
are nondecreasing, the latter occurs if and only if
$u_i$
are nondecreasing, the latter occurs if and only if
![]() ${\mathbf{X}}(v_t) \in \textrm{span}_R(v_1,\ldots, v_t) + p^{u_{t+1} - u_t}R^n$
. Hence,
${\mathbf{X}}(v_t) \in \textrm{span}_R(v_1,\ldots, v_t) + p^{u_{t+1} - u_t}R^n$
. Hence,
The assumption
![]() $\textrm{span}_R(v_1) = \textrm{span}_R(b\bmod p^m)$
implies that the event
$\textrm{span}_R(v_1) = \textrm{span}_R(b\bmod p^m)$
implies that the event
![]() $\textrm{span}_R({\mathbf{X}}^{j-1} b \bmod p^m\,:\,j\leq 2) = \textrm{span}_R(p^{u_j}v_1\,:\,j\leq 2)$
only depends on
$\textrm{span}_R({\mathbf{X}}^{j-1} b \bmod p^m\,:\,j\leq 2) = \textrm{span}_R(p^{u_j}v_1\,:\,j\leq 2)$
only depends on
![]() ${\mathbf{X}}(v_1)$
. Similarly, continuing in an inductive fashion, the event
${\mathbf{X}}(v_1)$
. Similarly, continuing in an inductive fashion, the event
![]() $E$
only depends on
$E$
only depends on
![]() ${\mathbf{X}}(v_1),\ldots, {\mathbf{X}}(v_{t-1})$
. Hence, by the law of total probability,
${\mathbf{X}}(v_1),\ldots, {\mathbf{X}}(v_{t-1})$
. Hence, by the law of total probability,
 \begin{align}{\mathbb{P}}\bigl ({\mathbf{X}}(&v_t) \in \textrm{span}_R(v_1,\ldots, v_t) + p^{u_{t+1} - u_t}R^n \mid E\bigr ) \\ &={\mathbb{E}}\Bigl [{\mathbb{P}}\bigl ({\mathbf{X}}(v_t) \in \textrm{span}_R(v_1,\ldots, v_t) + p^{u_{t+1} - u_t}R^n \mid{\mathbf{X}}(v_1),\ldots, {\mathbf{X}}(v_{t-1})\bigr )\ \big \vert \ E\ \Bigr ].\nonumber \end{align}
\begin{align}{\mathbb{P}}\bigl ({\mathbf{X}}(&v_t) \in \textrm{span}_R(v_1,\ldots, v_t) + p^{u_{t+1} - u_t}R^n \mid E\bigr ) \\ &={\mathbb{E}}\Bigl [{\mathbb{P}}\bigl ({\mathbf{X}}(v_t) \in \textrm{span}_R(v_1,\ldots, v_t) + p^{u_{t+1} - u_t}R^n \mid{\mathbf{X}}(v_1),\ldots, {\mathbf{X}}(v_{t-1})\bigr )\ \big \vert \ E\ \Bigr ].\nonumber \end{align}
Recall that the entries of
![]() $\mathbf{X}$
are independent and
$\mathbf{X}$
are independent and
![]() $\textrm{Unif}\{0,1,\ldots, p^{m}-1 \}$
-distributed. This implies that
$\textrm{Unif}\{0,1,\ldots, p^{m}-1 \}$
-distributed. This implies that
![]() $\mathbf{X}$
induces a uniform random endomorphism of
$\mathbf{X}$
induces a uniform random endomorphism of
![]() $R^n$
. Hence, since it was assumed that
$R^n$
. Hence, since it was assumed that
![]() ${\textrm{rank}}_p(v_1,\ldots, v_t) = t$
, it holds that
${\textrm{rank}}_p(v_1,\ldots, v_t) = t$
, it holds that
![]() ${\mathbf{X}}(v_t)$
has a uniform distribution on
${\mathbf{X}}(v_t)$
has a uniform distribution on
![]() $R^n$
and is independent of
$R^n$
and is independent of
![]() ${\mathbf{X}}(v_1),\ldots, {\mathbf{X}}(v_{t-1})$
. Consequently, a counting argument yields that
${\mathbf{X}}(v_1),\ldots, {\mathbf{X}}(v_{t-1})$
. Consequently, a counting argument yields that
Combine (2.6)–(2.8) to establish (2.5). This proves (2.3). Further, (2.4) is an immediate consequence of (2.3) since
![]() $U_{t+1} = u_{t+1}$
if and only if
$U_{t+1} = u_{t+1}$
if and only if
![]() $U_{t+1} \geq u_{t+1}$
and
$U_{t+1} \geq u_{t+1}$
and
![]() $U_{t+1} \lt u_{t+1} + 1$
.
$U_{t+1} \lt u_{t+1} + 1$
.
2.3
The law of
 $\mathrm{coker}({\mathbf{W}})_{p^m}$
$\mathrm{coker}({\mathbf{W}})_{p^m}$
It now only remains to combine Corollary 2.2 and Lemma 2.4. This allows us to also determine the law of
![]() $\textrm{coker}({\mathbf{W}})_{p^m}$
when
$\textrm{coker}({\mathbf{W}})_{p^m}$
when
![]() $n$
is finite:
$n$
is finite:
Proposition 2.5.
Fix some
![]() $n\geq 1$
, let
$n\geq 1$
, let
![]() $\mathbf{X}$
be a
$\mathbf{X}$
be a
![]() ${\mathbb{Z}}^{n\times n}$
-valued random matrix with independent
${\mathbb{Z}}^{n\times n}$
-valued random matrix with independent
![]() ${\operatorname{Unif}}\{0,1,\ldots, p^{m} - 1\}$
-distributed entries, and let
${\operatorname{Unif}}\{0,1,\ldots, p^{m} - 1\}$
-distributed entries, and let
![]() $b\in{\mathbb{Z}}^{n}$
be a deterministic vector with
$b\in{\mathbb{Z}}^{n}$
be a deterministic vector with
![]() $b\not \equiv 0 \bmod p$
. Fix an integer
$b\not \equiv 0 \bmod p$
. Fix an integer
![]() $0\leq i_0 \leq n-1$
.
$0\leq i_0 \leq n-1$
.
Pick integers
![]() $0 = \lambda _1 \leq \lambda _2 \leq \ldots \leq \lambda _n \leq m$
and denote
$0 = \lambda _1 \leq \lambda _2 \leq \ldots \leq \lambda _n \leq m$
and denote
![]() $\delta _i = \lambda _{n-i+1} - \lambda _{n-i}$
. Assume that
$\delta _i = \lambda _{n-i+1} - \lambda _{n-i}$
. Assume that
![]() $\lambda _{i} \lt m$
if and only if
$\lambda _{i} \lt m$
if and only if
![]() $i \leq n-i_0$
. Then, as Abelian groups,
$i \leq n-i_0$
. Then, as Abelian groups,
 \begin{align*}{\mathbb{P}}\left({\operatorname{coker}}({\mathbf{W}})_{p^m} \cong \bigoplus _{i=1}^n \frac{{\mathbb{Z}}}{p^{\lambda _i}{\mathbb{Z}}}\right) = \prod _{i=i_0}^{n-2} \left(1-p^{-(i+1)}\right)\prod _{j=1}^{n-1} p^{-j \delta _j}. \end{align*}
\begin{align*}{\mathbb{P}}\left({\operatorname{coker}}({\mathbf{W}})_{p^m} \cong \bigoplus _{i=1}^n \frac{{\mathbb{Z}}}{p^{\lambda _i}{\mathbb{Z}}}\right) = \prod _{i=i_0}^{n-2} \left(1-p^{-(i+1)}\right)\prod _{j=1}^{n-1} p^{-j \delta _j}. \end{align*}
Proof. By Corollary 2.2 and the assumption that
![]() $\lambda _i \lt m$
for every
$\lambda _i \lt m$
for every
![]() $i\leq n-i_0$
and
$i\leq n-i_0$
and
![]() $\lambda _{i} = m$
for every
$\lambda _{i} = m$
for every
![]() $i \gt n-i_0$
,
$i \gt n-i_0$
,
Recall that
![]() $\delta _{i} = \lambda _{n-i+1} - \lambda _{n-i}$
. Hence, using that
$\delta _{i} = \lambda _{n-i+1} - \lambda _{n-i}$
. Hence, using that
![]() $U_1 = 0$
together with (2.4) from Lemma 2.4, which is applicable due to the assumption that
$U_1 = 0$
together with (2.4) from Lemma 2.4, which is applicable due to the assumption that
![]() $\lambda _i \lt m$
for every
$\lambda _i \lt m$
for every
![]() $i \leq n-i_0$
,
$i \leq n-i_0$
,
 \begin{align}{\mathbb{P}}\bigl (U_i = \lambda _i,\, \forall i \in \{1,\ldots, n-i_0 \} \bigr ) &=\prod _{i=i_0}^{n-2}{\mathbb{P}}(U_{n-i} = U_{n-i-1} + \delta _{i+1} \mid U_j = \lambda _j, \, \forall j\lt n-i) \nonumber \\ &=\prod _{i=i_0}^{n-2} \big(1-p^{-(i+1)}\big) p^{-(i+1)\delta _{i+1}}. \end{align}
\begin{align}{\mathbb{P}}\bigl (U_i = \lambda _i,\, \forall i \in \{1,\ldots, n-i_0 \} \bigr ) &=\prod _{i=i_0}^{n-2}{\mathbb{P}}(U_{n-i} = U_{n-i-1} + \delta _{i+1} \mid U_j = \lambda _j, \, \forall j\lt n-i) \nonumber \\ &=\prod _{i=i_0}^{n-2} \big(1-p^{-(i+1)}\big) p^{-(i+1)\delta _{i+1}}. \end{align}
If
![]() $i_0 = 0$
, then the second probability in (2.9) is equal to one since there is no
$i_0 = 0$
, then the second probability in (2.9) is equal to one since there is no
![]() $i$
satisfying
$i$
satisfying
![]() $n + 1\leq i \leq n$
. In this case, the combination of (2.9) and (2.10) concludes the proof.
$n + 1\leq i \leq n$
. In this case, the combination of (2.9) and (2.10) concludes the proof.
Now suppose that
![]() $i_0 \gt 0$
. Then, it holds that
$i_0 \gt 0$
. Then, it holds that
![]() $U_i \geq m$
for all
$U_i \geq m$
for all
![]() $i\gt n-i_0$
if and only if
$i\gt n-i_0$
if and only if
![]() $U_{n-i_0 + 1} \geq m$
. Hence, using (2.3) from Lemma 2.4 and recalling that
$U_{n-i_0 + 1} \geq m$
. Hence, using (2.3) from Lemma 2.4 and recalling that
![]() $m = \lambda _{n-i_0} + \delta _{i_0}$
,
$m = \lambda _{n-i_0} + \delta _{i_0}$
,
 \begin{align}{\mathbb{P}}\bigl (U_i\geq m,\, \forall i \in \{n-i_0 +1,\ldots, n \}{}&{}\mid U_i = \lambda _i,\, \forall i\in \{1,\ldots, n-i_0 \}\bigr )\\ &={\mathbb{P}}(U_{n-i_0 +1} \geq m \mid U_i = \lambda _i,\, \forall i\in \{1,\ldots, n-i_0 \} \bigr )\nonumber \\ &=p^{-i_0\delta _{i_0}}.\nonumber \end{align}
\begin{align}{\mathbb{P}}\bigl (U_i\geq m,\, \forall i \in \{n-i_0 +1,\ldots, n \}{}&{}\mid U_i = \lambda _i,\, \forall i\in \{1,\ldots, n-i_0 \}\bigr )\\ &={\mathbb{P}}(U_{n-i_0 +1} \geq m \mid U_i = \lambda _i,\, \forall i\in \{1,\ldots, n-i_0 \} \bigr )\nonumber \\ &=p^{-i_0\delta _{i_0}}.\nonumber \end{align}
Remark
![]() $p^{-i_0\delta _{i_0}}=\prod _{i=1}^{i_0} p^{-i \delta _i}$
since the assumption that
$p^{-i_0\delta _{i_0}}=\prod _{i=1}^{i_0} p^{-i \delta _i}$
since the assumption that
![]() $\lambda _i = m = \lambda _{i+1}$
for all
$\lambda _i = m = \lambda _{i+1}$
for all
![]() $i\gt n-i_0$
ensures that
$i\gt n-i_0$
ensures that
![]() $\delta _{i} = 0$
for every
$\delta _{i} = 0$
for every
![]() $i\lt i_0$
. The combination of (2.9)–(2.11) hence concludes the proof.
$i\lt i_0$
. The combination of (2.9)–(2.11) hence concludes the proof.
Proof of Theorem 1.2. Let
![]() $\tilde{\lambda }_i \,:\!=\, 0$
for
$\tilde{\lambda }_i \,:\!=\, 0$
for
![]() $i \in \{1,\ldots, n-\ell \}$
and let
$i \in \{1,\ldots, n-\ell \}$
and let
![]() $\tilde{\lambda }_{i} \,:\!=\, \lambda _{i -(n-\ell )}$
for
$\tilde{\lambda }_{i} \,:\!=\, \lambda _{i -(n-\ell )}$
for
![]() $i\geq n-\ell +1$
. The result then follows by considering the probability that
$i\geq n-\ell +1$
. The result then follows by considering the probability that
![]() $\textrm{coker}({\mathbf{W}})_{p^m} \cong \oplus _{i=1}^n{\mathbb{Z}}/p^{\tilde{\lambda }_i}{\mathbb{Z}}$
in Proposition 2.5 and taking the limit
$\textrm{coker}({\mathbf{W}})_{p^m} \cong \oplus _{i=1}^n{\mathbb{Z}}/p^{\tilde{\lambda }_i}{\mathbb{Z}}$
in Proposition 2.5 and taking the limit
![]() $n\to \infty$
.
$n\to \infty$
.
3. Proof of Theorem 1.3
We establish a more general result than Theorem 1.3 and study the limiting law of the
![]() ${\mathbb{Z}}[x]$
-module
${\mathbb{Z}}[x]$
-module
![]() $\textrm{coker}(\tilde{{\mathbf{W}}})$
where
$\textrm{coker}(\tilde{{\mathbf{W}}})$
where
![]() $\tilde{{\mathbf{W}}} \,:\!=\, ({\mathbf{X}}^{j-1}{\mathbf{B}})_{j=1}^n$
is the
$\tilde{{\mathbf{W}}} \,:\!=\, ({\mathbf{X}}^{j-1}{\mathbf{B}})_{j=1}^n$
is the
![]() $n\times nk$
matrix associated to a deterministic
$n\times nk$
matrix associated to a deterministic
![]() $n\times k$
matrix
$n\times k$
matrix
![]() $\mathbf{B}$
for some fixed
$\mathbf{B}$
for some fixed
![]() $k$
. For future reference, let us here state all relevant assumptions:
$k$
. For future reference, let us here state all relevant assumptions:
-
(A1) For every
 $n\geq 1$
, let
$n\geq 1$
, let
 $\mathbf{X}$
be a
$\mathbf{X}$
be a
 ${\mathbb{Z}}^{n\times n}$
-valued random matrix with independent entries such that each entry is
${\mathbb{Z}}^{n\times n}$
-valued random matrix with independent entries such that each entry is
 $\alpha _n$
-balanced mod
$\alpha _n$
-balanced mod
 $\mathscr{P}$
.
$\mathscr{P}$
. -
(A2) Fix some
 $k\geq 1$
. For every
$k\geq 1$
. For every
 $n\geq k$
, let
$n\geq k$
, let
 ${\mathbf{B}}\in{\mathbb{Z}}^{n\times k}$
be a deterministic matrix such that
${\mathbf{B}}\in{\mathbb{Z}}^{n\times k}$
be a deterministic matrix such that
 ${\mathbf{B}} \bmod p$
has rank
${\mathbf{B}} \bmod p$
has rank
 $k$
over
$k$
over
 ${\mathbb{F}}_p$
for every
${\mathbb{F}}_p$
for every
 $p\in \mathscr{P}$
. We denote
$p\in \mathscr{P}$
. We denote
 $\tilde{{\mathbf{W}}} \,:\!=\, ({\mathbf{X}}^{j-1}{\mathbf{B}})_{j=1}^n$
and write
$\tilde{{\mathbf{W}}} \,:\!=\, ({\mathbf{X}}^{j-1}{\mathbf{B}})_{j=1}^n$
and write
 $\textrm{coker}(\tilde{{\mathbf{W}}}) \,:\!=\,{\mathbb{Z}}^n/\tilde{{\mathbf{W}}}({\mathbb{Z}}^{nk})$
.
$\textrm{coker}(\tilde{{\mathbf{W}}}) \,:\!=\,{\mathbb{Z}}^n/\tilde{{\mathbf{W}}}({\mathbb{Z}}^{nk})$
. -
(A3) Assume that
 $\lim _{n\to \infty }n\alpha _n/\ln (n)= \infty$
.
$\lim _{n\to \infty }n\alpha _n/\ln (n)= \infty$
.
The desired result, describing the limiting distribution of
![]() $\textrm{coker}(\tilde{{\mathbf{W}}})_{p^m,Q}$
under these assumptions, is given in Proposition 3.13.
$\textrm{coker}(\tilde{{\mathbf{W}}})_{p^m,Q}$
under these assumptions, is given in Proposition 3.13.
As was outlined in Section 1.2, we rely on the category-theoretic moment method. The main ingredient required for the proof is correspondingly an estimate on the moments of
![]() $\textrm{coker}(\tilde{{\mathbf{W}}})$
:
$\textrm{coker}(\tilde{{\mathbf{W}}})$
:
Proposition 3.1.
Adopt assumptions (A1) to (A3). Then, for every finite
![]() ${\mathbb{Z}}[x]$
-module
${\mathbb{Z}}[x]$
-module
![]() $N$
such that all prime divisors of
$N$
such that all prime divisors of
![]() $\#N$
are in
$\#N$
are in
![]() $\mathscr{P}$
,
$\mathscr{P}$
,
We prove Proposition 3.1 in Section 3.1 and then use a general-purpose result of Sawin and Wood [Reference Sawin and Wood20, Lemma 6.3] to solve the associated moment problem in Section 3.2.
Remark 3.2. The assumption in Proposition 3.1 that all prime divisors of
![]() $\#N$
are in
$\#N$
are in
![]() $\mathscr{P}$
cannot be removed. Indeed, recall that (A1) and (A2) only make assumptions regarding
$\mathscr{P}$
cannot be removed. Indeed, recall that (A1) and (A2) only make assumptions regarding
![]() ${\textrm{rank}}_p({\mathbf{B}})$
and the balanced nature of the entries of
${\textrm{rank}}_p({\mathbf{B}})$
and the balanced nature of the entries of
![]() $\mathbf{X}$
at primes
$\mathbf{X}$
at primes
![]() $p \in \mathscr{P}$
.
$p \in \mathscr{P}$
.
So, for instance, at
![]() $p\notin \mathscr{P}$
it could occur that
$p\notin \mathscr{P}$
it could occur that
![]() ${\mathbb{P}}({\mathbf{X}} \equiv 0 \bmod p) = 1$
and
${\mathbb{P}}({\mathbf{X}} \equiv 0 \bmod p) = 1$
and
![]() ${\mathbf{B}} = 0\bmod p$
in which case
${\mathbf{B}} = 0\bmod p$
in which case
![]() ${\mathbb{E}}[\# \textrm{Sur}_{{\mathbb{Z}}[x]}(\textrm{coker}(\tilde{{\mathbf{W}}}), N)] = p^n -1$
with
${\mathbb{E}}[\# \textrm{Sur}_{{\mathbb{Z}}[x]}(\textrm{coker}(\tilde{{\mathbf{W}}}), N)] = p^n -1$
with
![]() $N ={\mathbb{F}}_p[x]/x{\mathbb{F}}_{p}[x]$
. In particular, it then holds that
$N ={\mathbb{F}}_p[x]/x{\mathbb{F}}_{p}[x]$
. In particular, it then holds that
![]() $\lim _{n\to \infty }{\mathbb{E}}[\# \textrm{Sur}_{{\mathbb{Z}}[x]}(\textrm{coker}(\tilde{{\mathbf{W}}}), N)] = \infty$
, which is incompatible with the conclusion of Proposition 3.1.
$\lim _{n\to \infty }{\mathbb{E}}[\# \textrm{Sur}_{{\mathbb{Z}}[x]}(\textrm{coker}(\tilde{{\mathbf{W}}}), N)] = \infty$
, which is incompatible with the conclusion of Proposition 3.1.
Remark 3.3. There is a sense in which
![]() $\textrm{coker}(\tilde{{\mathbf{W}}})$
is a fairly natural random algebraic object to study. Note that
$\textrm{coker}(\tilde{{\mathbf{W}}})$
is a fairly natural random algebraic object to study. Note that
![]() ${\mathbf{W}}({\mathbb{Z}}^{nk})$
is exactly the
${\mathbf{W}}({\mathbb{Z}}^{nk})$
is exactly the
![]() ${\mathbb{Z}}[x]$
-submodule of
${\mathbb{Z}}[x]$
-submodule of
![]() ${\mathbb{Z}}^n$
generated by the columns of
${\mathbb{Z}}^n$
generated by the columns of
![]() $\mathbf{B}$
. Hence, introducing formal symbols
$\mathbf{B}$
. Hence, introducing formal symbols
![]() $e_1,\ldots, e_n$
, we have
$e_1,\ldots, e_n$
, we have
 \begin{align} \operatorname{coker}(\tilde{{\mathbf{W}}}) \cong \left(e_1,\ldots, e_n\,:\, xe_j = \sum _{i=1}^n{\mathbf{X}}_{i,j} e_i,\, \sum _{i=1}^n{\mathbf{B}}_{i,r} e_i = 0,\, \forall i\leq n,\, \forall r\leq k \right) \end{align}
\begin{align} \operatorname{coker}(\tilde{{\mathbf{W}}}) \cong \left(e_1,\ldots, e_n\,:\, xe_j = \sum _{i=1}^n{\mathbf{X}}_{i,j} e_i,\, \sum _{i=1}^n{\mathbf{B}}_{i,r} e_i = 0,\, \forall i\leq n,\, \forall r\leq k \right) \end{align}
as
![]() ${\mathbb{Z}}[x]$
-modules. So,
${\mathbb{Z}}[x]$
-modules. So,
![]() $\textrm{coker}(\tilde{{\mathbf{W}}})$
corresponds to the finitely presented
$\textrm{coker}(\tilde{{\mathbf{W}}})$
corresponds to the finitely presented
![]() ${\mathbb{Z}}[x]$
-module, which is found when one considers
${\mathbb{Z}}[x]$
-module, which is found when one considers
![]() $n$
generators, imposes a random action for
$n$
generators, imposes a random action for
![]() $x$
specified by
$x$
specified by
![]() $\mathbf{X}$
, and imposes
$\mathbf{X}$
, and imposes
![]() $k\geq 1$
additional deterministic constraints specified by
$k\geq 1$
additional deterministic constraints specified by
![]() $\mathbf{B}$
.
$\mathbf{B}$
.
3.1
Computing the limiting
 $N$
-moments
$N$
-moments
Let
![]() $N$
be a deterministic
$N$
be a deterministic
![]() ${\mathbb{Z}}[x]$
-module such that all prime divisors of
${\mathbb{Z}}[x]$
-module such that all prime divisors of
![]() $\#N$
are in
$\#N$
are in
![]() $\mathscr{P}$
. We may consider
$\mathscr{P}$
. We may consider
![]() $\mathbf{X}$
as a random element of
$\mathbf{X}$
as a random element of
![]() ${\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,{\mathbb{Z}}^n)$
, consider
${\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,{\mathbb{Z}}^n)$
, consider
![]() $\mathbf{B}$
as a deterministic element of
$\mathbf{B}$
as a deterministic element of
![]() ${\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^k,{\mathbb{Z}}^n)$
, and consider
${\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^k,{\mathbb{Z}}^n)$
, and consider
![]() $x$
as inducing an element of
$x$
as inducing an element of
![]() ${\textrm{Hom}}_{{\mathbb{Z}}}(N,N)$
. Here, note that
${\textrm{Hom}}_{{\mathbb{Z}}}(N,N)$
. Here, note that
![]() ${\textrm{Hom}}_{{\mathbb{Z}}}(\cdot, \cdot )$
simply returns the set of group morphisms since a
${\textrm{Hom}}_{{\mathbb{Z}}}(\cdot, \cdot )$
simply returns the set of group morphisms since a
![]() $\mathbb{Z}$
-module and an Abelian group are the same thing.
$\mathbb{Z}$
-module and an Abelian group are the same thing.
Now observe that a morphism of Abelian groups
![]() $F\,:\,{\mathbb{Z}}^n \to N$
descends to a morphism of
$F\,:\,{\mathbb{Z}}^n \to N$
descends to a morphism of
![]() ${\mathbb{Z}}[x]$
-modules
${\mathbb{Z}}[x]$
-modules
![]() $\overline{F}\,:\,\textrm{coker}(\tilde{{\mathbf{W}}}) \to N$
if and only if the compositions of
$\overline{F}\,:\,\textrm{coker}(\tilde{{\mathbf{W}}}) \to N$
if and only if the compositions of
![]() $F$
with
$F$
with
![]() ${\mathbf{B}},{\mathbf{X}}$
, and
${\mathbf{B}},{\mathbf{X}}$
, and
![]() $x$
satisfy
$x$
satisfy
![]() $F{\mathbf{B}} = 0$
and
$F{\mathbf{B}} = 0$
and
![]() $F{\mathbf{X}} = xF$
. Moreover, every
$F{\mathbf{X}} = xF$
. Moreover, every
![]() ${\mathbb{Z}}[x]$
-module morphism
${\mathbb{Z}}[x]$
-module morphism
![]() $\overline{F}\,:\,\textrm{coker}(\tilde{{\mathbf{W}}}) \to N$
arises from some unique
$\overline{F}\,:\,\textrm{coker}(\tilde{{\mathbf{W}}}) \to N$
arises from some unique
![]() $F\,:\,{\mathbb{Z}}^n\to N$
in this fashion. Consequently, since surjectivity is conserved,
$F\,:\,{\mathbb{Z}}^n\to N$
in this fashion. Consequently, since surjectivity is conserved,
Let us here emphasise that, while (3.3) was relatively easy to prove, the simplification which this step offers is significant. Indeed, observe that the joint law of the entries of
![]() $\tilde{{\mathbf{W}}}$
is not easy to understand since these entries are nontrivial algebraic combinations of the entries of
$\tilde{{\mathbf{W}}}$
is not easy to understand since these entries are nontrivial algebraic combinations of the entries of
![]() $\mathbf{X}$
and
$\mathbf{X}$
and
![]() $\mathbf{B}$
. On the other hand,
$\mathbf{B}$
. On the other hand,
![]() $F{\mathbf{X}} = xF$
is a linear equation in terms of
$F{\mathbf{X}} = xF$
is a linear equation in terms of
![]() $\mathbf{X}$
and hence fairly explicit.
$\mathbf{X}$
and hence fairly explicit.
The strategy that we use to estimate the
![]() $N$
-moments from here on is as follows. We show that there are approximately
$N$
-moments from here on is as follows. We show that there are approximately
![]() $(\#N)^{n - k}$
surjections
$(\#N)^{n - k}$
surjections
![]() $F\,:\,{\mathbb{Z}}^n\to N$
with
$F\,:\,{\mathbb{Z}}^n\to N$
with
![]() $F{\mathbf{B}} = 0$
in Section 3.1.1. Subsequently, we show that
$F{\mathbf{B}} = 0$
in Section 3.1.1. Subsequently, we show that
![]() ${\mathbb{P}}(F{\mathbf{X}} = xF) \approx (\# N)^{-n}$
for most terms in (3.3) in Section 3.1.2, and we show that the remaining terms give a negligible contribution in Section 3.1.3. Finally, we combine these ingredients to conclude the proof of Proposition 3.1 in Section 3.1.4.
${\mathbb{P}}(F{\mathbf{X}} = xF) \approx (\# N)^{-n}$
for most terms in (3.3) in Section 3.1.2, and we show that the remaining terms give a negligible contribution in Section 3.1.3. Finally, we combine these ingredients to conclude the proof of Proposition 3.1 in Section 3.1.4.
3.1.1. Estimate on the number of surjections satisfying
 $F{\mathbf{B}} = 0$
$F{\mathbf{B}} = 0$
The exponent of a finite Abelian group
![]() $G$
is the smallest positive integer
$G$
is the smallest positive integer
![]() $\exp (G)\geq 1$
such that
$\exp (G)\geq 1$
such that
![]() $\exp (G)G = 0$
. Note that
$\exp (G)G = 0$
. Note that
![]() $p\mid \exp (G)$
if and only if
$p\mid \exp (G)$
if and only if
![]() $p\mid \# G$
.
$p\mid \# G$
.
Lemma 3.4.
Let
![]() $G$
be a finite Abelian group and let
$G$
be a finite Abelian group and let
![]() ${\mathbf{B}} \in{\operatorname{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^k,{\mathbb{Z}}^n)$
be such that
${\mathbf{B}} \in{\operatorname{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^k,{\mathbb{Z}}^n)$
be such that
![]() ${\operatorname{rank}}_p({\mathbf{B}}) = k$
for every prime divisor
${\operatorname{rank}}_p({\mathbf{B}}) = k$
for every prime divisor
![]() $p$
of
$p$
of
![]() $\exp (G)$
. Then, there exists a constant
$\exp (G)$
. Then, there exists a constant
![]() $C \gt 0$
depending only on
$C \gt 0$
depending only on
![]() $G$
such that for all
$G$
such that for all
![]() $n\geq k$
$n\geq k$
Proof. We first argue that we can replace
![]() $\textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)$
by
$\textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)$
by
![]() ${\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)$
up to a negligible error. If a morphism
${\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)$
up to a negligible error. If a morphism
![]() $F\,:\,{\mathbb{Z}}^n\to G$
is not surjective then there exists some proper subgroup
$F\,:\,{\mathbb{Z}}^n\to G$
is not surjective then there exists some proper subgroup
![]() $H\subsetneq G$
such that
$H\subsetneq G$
such that
![]() $F({\mathbb{Z}}^n) = H$
. Hence, since
$F({\mathbb{Z}}^n) = H$
. Hence, since
![]() $\#{\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,H) = (\# H)^n$
,
$\#{\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,H) = (\# H)^n$
,
Denote
![]() $S_G$
for the number of proper subgroups of
$S_G$
for the number of proper subgroups of
![]() $G$
. Then, since
$G$
. Then, since
![]() $\#H \leq \# G/2$
by
$\#H \leq \# G/2$
by
![]() $H$
being a proper subgroup,
$H$
being a proper subgroup,
 \begin{align} \lvert \#\{F\in{\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)&\,:\, F{\mathbf{B}} = 0\} - \#\{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)\,:\, F{\mathbf{B}} = 0\} \rvert \\ & \leq \#({\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G) \setminus \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)) \leq S_G \Bigl (\frac{\#G}{2}\Bigr )^{n}. \nonumber \end{align}
\begin{align} \lvert \#\{F\in{\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)&\,:\, F{\mathbf{B}} = 0\} - \#\{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)\,:\, F{\mathbf{B}} = 0\} \rvert \\ & \leq \#({\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G) \setminus \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)) \leq S_G \Bigl (\frac{\#G}{2}\Bigr )^{n}. \nonumber \end{align}
We next argue that
![]() $\#\{F\in{\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)\,:\, F{\mathbf{B}} = 0\} = (\#G)^{n-k}$
. (This is not immediate because the columns
$\#\{F\in{\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)\,:\, F{\mathbf{B}} = 0\} = (\#G)^{n-k}$
. (This is not immediate because the columns
![]() $b_1,\ldots, b_k$
of
$b_1,\ldots, b_k$
of
![]() $\mathbf{B}$
are not necessarily part of a
$\mathbf{B}$
are not necessarily part of a
![]() $\mathbb{Z}$
-module basis for
$\mathbb{Z}$
-module basis for
![]() ${\mathbb{Z}}^n$
.)
${\mathbb{Z}}^n$
.)
Let
![]() ${\mathbf{B}} ={\mathbf{U}}{\mathbf{D}}{\mathbf{V}}$
be the Smith normal form of
${\mathbf{B}} ={\mathbf{U}}{\mathbf{D}}{\mathbf{V}}$
be the Smith normal form of
![]() $\mathbf{B}$
. This means that
$\mathbf{B}$
. This means that
![]() ${\mathbf{U}} \in{\mathbb{Z}}^{n\times n}$
and
${\mathbf{U}} \in{\mathbb{Z}}^{n\times n}$
and
![]() ${\mathbf{V}} \in{\mathbb{Z}}^{k\times k}$
are matrices with
${\mathbf{V}} \in{\mathbb{Z}}^{k\times k}$
are matrices with
![]() $\det ({\mathbf{U}}), \det ({\mathbf{V}})\in \{-1,1\}$
and
$\det ({\mathbf{U}}), \det ({\mathbf{V}})\in \{-1,1\}$
and
![]() $\mathbf{D}$
is an
$\mathbf{D}$
is an
![]() $n\times k$
diagonal matrix with integer diagonal entries satisfying
$n\times k$
diagonal matrix with integer diagonal entries satisfying
![]() $d_1 \mid d_2 \mid \ldots \mid d_k$
. For brevity, denote
$d_1 \mid d_2 \mid \ldots \mid d_k$
. For brevity, denote
![]() $a \,:\!=\, \exp (G)$
. For every
$a \,:\!=\, \exp (G)$
. For every
![]() $p\mid a$
, the assumption that
$p\mid a$
, the assumption that
![]() ${\textrm{rank}}_p({\mathbf{B}}) = k$
implies that
${\textrm{rank}}_p({\mathbf{B}}) = k$
implies that
![]() $d_i \not \equiv 0 \bmod p$
. It follows that the
$d_i \not \equiv 0 \bmod p$
. It follows that the
![]() $d_i$
are multiplicative units for
$d_i$
are multiplicative units for
![]() ${\mathbb{Z}}/a{\mathbb{Z}}$
. Hence, the matrix
${\mathbb{Z}}/a{\mathbb{Z}}$
. Hence, the matrix
![]() ${\mathbf{D}}^{\prime} \,:\!=\, \textrm{diag}(d_1,\ldots, d_k)$
is invertible in
${\mathbf{D}}^{\prime} \,:\!=\, \textrm{diag}(d_1,\ldots, d_k)$
is invertible in
![]() $({\mathbb{Z}}/a{\mathbb{Z}})^{k\times k}$
. Further, note that
$({\mathbb{Z}}/a{\mathbb{Z}})^{k\times k}$
. Further, note that
![]() $\mathbf{U}$
and
$\mathbf{U}$
and
![]() $\mathbf{V}$
are invertible over
$\mathbf{V}$
are invertible over
![]() $\mathbb{Z}$
. Hence, if
$\mathbb{Z}$
. Hence, if
![]() $u_1,\ldots, u_n$
are the columns of
$u_1,\ldots, u_n$
are the columns of
![]() $\mathbf{U}$
, then the reductions to
$\mathbf{U}$
, then the reductions to
![]() $({\mathbb{Z}}/a{\mathbb{Z}})^n$
determine a
$({\mathbb{Z}}/a{\mathbb{Z}})^n$
determine a
![]() $({\mathbb{Z}}/a{\mathbb{Z}})$
-module basis, and the reduction of
$({\mathbb{Z}}/a{\mathbb{Z}})$
-module basis, and the reduction of
![]() ${\mathbf{D}}^{\prime}{\mathbf{V}}$
to
${\mathbf{D}}^{\prime}{\mathbf{V}}$
to
![]() $({\mathbb{Z}}/a{\mathbb{Z}})^{k\times k}$
is invertible. Consequently, since
$({\mathbb{Z}}/a{\mathbb{Z}})^{k\times k}$
is invertible. Consequently, since
![]() ${\mathbf{B}} = (u_1,\ldots, u_k){\mathbf{D}}^{\prime}{\mathbf{V}}$
, the reductions of
${\mathbf{B}} = (u_1,\ldots, u_k){\mathbf{D}}^{\prime}{\mathbf{V}}$
, the reductions of
![]() $b_1,\ldots, b_k$
together with the reductions of the
$b_1,\ldots, b_k$
together with the reductions of the
![]() $u_i$
with
$u_i$
with
![]() $i\geq k+1$
determine a
$i\geq k+1$
determine a
![]() $({\mathbb{Z}}/a{\mathbb{Z}})$
-module basis for
$({\mathbb{Z}}/a{\mathbb{Z}})$
-module basis for
![]() $({\mathbb{Z}}/a{\mathbb{Z}})^n$
.
$({\mathbb{Z}}/a{\mathbb{Z}})^n$
.
Denote
![]() $\pi \,:\,{\mathbb{Z}}^n \to ({\mathbb{Z}}/a{\mathbb{Z}})^n$
for the reduction map. Then, since
$\pi \,:\,{\mathbb{Z}}^n \to ({\mathbb{Z}}/a{\mathbb{Z}})^n$
for the reduction map. Then, since
![]() $a = \exp (G)$
, it holds for every
$a = \exp (G)$
, it holds for every
![]() $F\in{\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)$
that there is some unique
$F\in{\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)$
that there is some unique
![]() $\overline{F}\in{\textrm{Hom}}_{{\mathbb{Z}}/a{\mathbb{Z}}}(({\mathbb{Z}}/a{\mathbb{Z}})^n, G)$
with
$\overline{F}\in{\textrm{Hom}}_{{\mathbb{Z}}/a{\mathbb{Z}}}(({\mathbb{Z}}/a{\mathbb{Z}})^n, G)$
with
![]() $F = \overline{F} \circ \pi$
. Recall that for any ring
$F = \overline{F} \circ \pi$
. Recall that for any ring
![]() $R$
an
$R$
an
![]() $R$
-module morphism from a free
$R$
-module morphism from a free
![]() $R$
-module to an arbitrary
$R$
-module to an arbitrary
![]() $R$
-module may be specified uniquely by arbitrarily specifying the images of the basis elements. Consequently, since the
$R$
-module may be specified uniquely by arbitrarily specifying the images of the basis elements. Consequently, since the
![]() $\pi (b_i)$
are part of a
$\pi (b_i)$
are part of a
![]() $({\mathbb{Z}}/a{\mathbb{Z}})$
-module basis,
$({\mathbb{Z}}/a{\mathbb{Z}})$
-module basis,
Combine (3.5) with (3.6) and set
![]() $C \,:\!=\, S_G$
to conclude the proof.
$C \,:\!=\, S_G$
to conclude the proof.
We next estimate
![]() ${\mathbb{P}}(F{\mathbf{X}} = xF)$
. The quality of the estimates will be better when
${\mathbb{P}}(F{\mathbf{X}} = xF)$
. The quality of the estimates will be better when
![]() $F$
is ‘very surjective’. To make this precise, we rely on a notion of codes which is due to Wood [Reference Wood32] and a notion of robust morphisms which is due to Nguyen and Wood [Reference Nguyen and Wood15].
$F$
is ‘very surjective’. To make this precise, we rely on a notion of codes which is due to Wood [Reference Wood32] and a notion of robust morphisms which is due to Nguyen and Wood [Reference Nguyen and Wood15].
3.1.2. Estimate for codes
Let
![]() $e_1,\ldots, e_n \in{\mathbb{Z}}^n$
be the standard basis vectors. For any
$e_1,\ldots, e_n \in{\mathbb{Z}}^n$
be the standard basis vectors. For any
![]() $\sigma \subseteq \{1,\ldots, n \}$
, write
$\sigma \subseteq \{1,\ldots, n \}$
, write
![]() $V_{\sigma }\,:\!=\, \textrm{span}_{{\mathbb{Z}}}(e_i : i \in \sigma )$
for the
$V_{\sigma }\,:\!=\, \textrm{span}_{{\mathbb{Z}}}(e_i : i \in \sigma )$
for the
![]() $\mathbb{Z}$
-submodule of
$\mathbb{Z}$
-submodule of
![]() ${\mathbb{Z}}^n$
consisting of vectors whose nonzero coordinates are in
${\mathbb{Z}}^n$
consisting of vectors whose nonzero coordinates are in
![]() $\sigma$
. We abbreviate
$\sigma$
. We abbreviate
![]() $V_{\setminus \sigma } \,:\!=\, V_{\{1,\ldots, n \}\setminus \sigma }$
.
$V_{\setminus \sigma } \,:\!=\, V_{\{1,\ldots, n \}\setminus \sigma }$
.
Definition 3.5.
Let
![]() $G$
be an Abelian group. Then,
$G$
be an Abelian group. Then,
![]() $F\in{\operatorname{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)$
is called a code of distance
$F\in{\operatorname{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)$
is called a code of distance
![]() $w\geq 1$
if for every
$w\geq 1$
if for every
![]() $\sigma \subseteq \{1,\ldots, n \}$
with
$\sigma \subseteq \{1,\ldots, n \}$
with
![]() $\# \sigma \lt w$
one has
$\# \sigma \lt w$
one has
![]() $F(V_{\setminus \sigma }) = G$
.
$F(V_{\setminus \sigma }) = G$
.
The foregoing definition may also be applied to
![]() ${\mathbb{Z}}[x]$
-modules since these can be viewed as Abelian groups through the
${\mathbb{Z}}[x]$
-modules since these can be viewed as Abelian groups through the
![]() $\mathbb{Z}$
-module structure.
$\mathbb{Z}$
-module structure.
Lemma 3.6.
Adopt assumptions (A1) and (A3), and fix a
![]() ${\mathbb{Z}}[x]$
-module
${\mathbb{Z}}[x]$
-module
![]() $N$
such that all prime divisors of
$N$
such that all prime divisors of
![]() $\#N$
are in
$\#N$
are in
![]() $\mathscr{P}$
. Then, for every
$\mathscr{P}$
. Then, for every
![]() $\delta \gt 0$
, there exist constants
$\delta \gt 0$
, there exist constants
![]() $C,c\gt 0$
such that for all
$C,c\gt 0$
such that for all
![]() $n\geq 1$
$n\geq 1$
 \begin{align} \sum _{\substack{F\in{\operatorname{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N)\\F\text{ a code of distance }\delta n}} \bigl \lvert{\mathbb{P}}(F{\mathbf{X}} = xF) - (\#N)^{-n}\bigr \rvert \leq C n^{-c}. \end{align}
\begin{align} \sum _{\substack{F\in{\operatorname{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N)\\F\text{ a code of distance }\delta n}} \bigl \lvert{\mathbb{P}}(F{\mathbf{X}} = xF) - (\#N)^{-n}\bigr \rvert \leq C n^{-c}. \end{align}
Proof. For any code
![]() $F$
and any
$F$
and any
![]() $A\in{\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N)$
, it is shown in [Reference Nguyen and Wood15, Lemma 4.7] that
$A\in{\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N)$
, it is shown in [Reference Nguyen and Wood15, Lemma 4.7] that
![]() $\lvert{\mathbb{P}}(F{\mathbf{X}} = A) -(\# N)^{-n} \rvert \leq C (\# N)^{-n} n^{-c}$
. Actually, strictly speaking, [Reference Nguyen and Wood15, Lemma 4.7] is stated for matrices that are
$\lvert{\mathbb{P}}(F{\mathbf{X}} = A) -(\# N)^{-n} \rvert \leq C (\# N)^{-n} n^{-c}$
. Actually, strictly speaking, [Reference Nguyen and Wood15, Lemma 4.7] is stated for matrices that are
![]() $\alpha _n$
-balanced at all primes, but only balancedness at primes dividing
$\alpha _n$
-balanced at all primes, but only balancedness at primes dividing
![]() $\#N$
is necessary for its proof. (Indeed, [Reference Nguyen and Wood15, Lemma 4.7] follows from [Reference Nguyen and Wood15, Lemma 4.5] whose proof may be found in [Reference Wood33, Lemma 2.1] and only requires the weaker condition; see [Reference Wood33, Definition 1].) The result now follows since there are at most
$\#N$
is necessary for its proof. (Indeed, [Reference Nguyen and Wood15, Lemma 4.7] follows from [Reference Nguyen and Wood15, Lemma 4.5] whose proof may be found in [Reference Wood33, Lemma 2.1] and only requires the weaker condition; see [Reference Wood33, Definition 1].) The result now follows since there are at most
![]() $\#{\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) = (\#N)^n$
summands in (3.7).
$\#{\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) = (\#N)^n$
summands in (3.7).
3.1.3. Estimate for non-codes
The contribution of terms in (3.3) corresponding to non-codes turns out to be negligible. It is however delicate to make this rigorous. The estimate that can be achieved on
![]() ${\mathbb{P}}(F{\mathbf{X}} = xF)$
for a generic non-code
${\mathbb{P}}(F{\mathbf{X}} = xF)$
for a generic non-code
![]() $F$
is, namely, insufficient to beat the combinatorial factor corresponding to the number of non-codes. Hence, a subdivision of the non-codes is required to balance the quality of the estimates against the combinatorial costs.
$F$
is, namely, insufficient to beat the combinatorial factor corresponding to the number of non-codes. Hence, a subdivision of the non-codes is required to balance the quality of the estimates against the combinatorial costs.
For an integer
![]() $d$
with prime factorisation
$d$
with prime factorisation
![]() $d = \prod _{i} p_i^{e_i}$
, denote
$d = \prod _{i} p_i^{e_i}$
, denote
![]() $\ell (d) \,:\!=\, \sum _{i} e_i$
. Given a subgroup
$\ell (d) \,:\!=\, \sum _{i} e_i$
. Given a subgroup
![]() $H\subseteq G$
, let
$H\subseteq G$
, let
![]() $[G\,:\,H]\,:\!=\, \#G/\#H$
denote the index of
$[G\,:\,H]\,:\!=\, \#G/\#H$
denote the index of
![]() $H$
in
$H$
in
![]() $G$
.
$G$
.
Definition 3.7.
Let
![]() $G$
be a finite Abelian group and let
$G$
be a finite Abelian group and let
![]() $\delta \gt 0$
be a scalar. Then,
$\delta \gt 0$
be a scalar. Then,
![]() $F\in{\operatorname{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)$
is called
$F\in{\operatorname{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)$
is called
![]() $\delta$
-robust for a subgroup
$\delta$
-robust for a subgroup
![]() $H\subseteq G$
if
$H\subseteq G$
if
![]() $H$
is minimal with the property that
$H$
is minimal with the property that
That is,
![]() $H$
satisfies
(3.8)
, and no strict subgroup
$H$
satisfies
(3.8)
, and no strict subgroup
![]() $H^{\prime} \subsetneq H$
satisfies
(3.8)
.
$H^{\prime} \subsetneq H$
satisfies
(3.8)
.
The main motivation for Definition 3.7 is the following property: if
![]() $F$
is
$F$
is
![]() $\delta$
-robust for
$\delta$
-robust for
![]() $H$
, then the restriction of
$H$
, then the restriction of
![]() $F$
to
$F$
to
![]() $V_{\sigma }$
with
$V_{\sigma }$
with
![]() $\sigma \,:\!=\, \{i\,:\, F(e_i) \in H \}$
is a code of distance
$\sigma \,:\!=\, \{i\,:\, F(e_i) \in H \}$
is a code of distance
![]() $\delta n$
when
$\delta n$
when
![]() $H$
is viewed as the codomain of this restriction. Indeed, suppose this were not the case. Then, there exists
$H$
is viewed as the codomain of this restriction. Indeed, suppose this were not the case. Then, there exists
![]() $\mu \subseteq \sigma$
with
$\mu \subseteq \sigma$
with
![]() $\# \mu \lt \delta n$
such that
$\# \mu \lt \delta n$
such that
![]() $H^{\prime} \,:\!=\, F(V_{\sigma \setminus \mu })$
is a strict subgroup of
$H^{\prime} \,:\!=\, F(V_{\sigma \setminus \mu })$
is a strict subgroup of
![]() $H$
. So, since
$H$
. So, since
![]() $[G\,:\,H^{\prime}] \geq [G\,:\,H] +1$
,
$[G\,:\,H^{\prime}] \geq [G\,:\,H] +1$
,
contradicting the minimality of
![]() $H$
.
$H$
.
In particular, any
![]() $F\in{\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)$
that is not a code of distance
$F\in{\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)$
that is not a code of distance
![]() $\delta n$
is not
$\delta n$
is not
![]() $\delta$
-robust for
$\delta$
-robust for
![]() $G$
. However, (3.8) is always satisfied when
$G$
. However, (3.8) is always satisfied when
![]() $G = H$
. This implies that any non-code has to be
$G = H$
. This implies that any non-code has to be
![]() $\delta$
-robust for some, not necessarily unique, proper subgroup of
$\delta$
-robust for some, not necessarily unique, proper subgroup of
![]() $G$
. Hence,
$G$
. Hence,
 \begin{align} \{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)\,:\,F &\text{ not a code of distance }\delta n \} \\ & \subseteq \bigcup _{H \subsetneq G} \{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)\,:\,F \text{ is }\delta \text{-robust for }H\}.\nonumber \end{align}
\begin{align} \{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)\,:\,F &\text{ not a code of distance }\delta n \} \\ & \subseteq \bigcup _{H \subsetneq G} \{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)\,:\,F \text{ is }\delta \text{-robust for }H\}.\nonumber \end{align}
We next establish an estimate on
![]() ${\mathbb{P}}(F{\mathbf{X}} = xF)$
when
${\mathbb{P}}(F{\mathbf{X}} = xF)$
when
![]() $F$
is
$F$
is
![]() $\delta$
-robust for some
$\delta$
-robust for some
![]() $H$
. The following lemma generalises [Reference Nguyen and Wood15, Lemma 4.11], which concerns a similar bound for
$H$
. The following lemma generalises [Reference Nguyen and Wood15, Lemma 4.11], which concerns a similar bound for
![]() ${\mathbb{P}}(F(Y) = 0)$
.
${\mathbb{P}}(F(Y) = 0)$
.
Lemma 3.8.
Fix scalars
![]() $\delta, \alpha \gt 0$
, an integer
$\delta, \alpha \gt 0$
, an integer
![]() $n \geq 1$
, and a finite Abelian group
$n \geq 1$
, and a finite Abelian group
![]() $G$
. Fix a proper subgroup
$G$
. Fix a proper subgroup
![]() $H\subsetneq G$
, denote
$H\subsetneq G$
, denote
![]() $d \,:\!=\, [G\,:\,H]$
, and consider a maximal chain of proper subgroups
$d \,:\!=\, [G\,:\,H]$
, and consider a maximal chain of proper subgroups
Consider a
![]() $\delta$
-robust morphism
$\delta$
-robust morphism
![]() $F\in{\operatorname{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)$
for
$F\in{\operatorname{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,G)$
for
![]() $H$
. For every
$H$
. For every
![]() $1 \leq j \leq \ell (d)$
denote
$1 \leq j \leq \ell (d)$
denote
![]() $p_j \,:\!=\, [G_{j-1} \,:\, G_{j}]$
and
$p_j \,:\!=\, [G_{j-1} \,:\, G_{j}]$
and
Abbreviate
![]() $a \,:\!=\, \exp (G)$
for the exponent of
$a \,:\!=\, \exp (G)$
for the exponent of
![]() $G$
. Then, for every
$G$
. Then, for every
![]() $g\in G$
and every
$g\in G$
and every
![]() ${\mathbb{Z}}^n$
-valued random vector
${\mathbb{Z}}^n$
-valued random vector
![]() $Y$
whose entries are independent and
$Y$
whose entries are independent and
![]() $\alpha$
-balanced modulo all prime divisors of
$\alpha$
-balanced modulo all prime divisors of
![]() $a$
,
$a$
,
 \begin{align}{\mathbb{P}}\bigl (F(Y) = g \bigr ) \leq &\left( (\#G)^{-1}d + \exp \left(-\alpha \delta n/a^2\right) \right) \prod _{j=1}^{\ell (d)}\left(p_j^{-1} + \frac{p_j -1}{p_j}\exp \left(-\alpha w_j/p_j^2\right) \right). \end{align}
\begin{align}{\mathbb{P}}\bigl (F(Y) = g \bigr ) \leq &\left( (\#G)^{-1}d + \exp \left(-\alpha \delta n/a^2\right) \right) \prod _{j=1}^{\ell (d)}\left(p_j^{-1} + \frac{p_j -1}{p_j}\exp \left(-\alpha w_j/p_j^2\right) \right). \end{align}
Proof. The strategy in this proof is to reduce to the case of codes where estimates are available from [Reference Nguyen and Wood15, Lemma 4.5]. Again, similar to the remarks in the proof of Lemma 3.6, that lemma is stated for the case where
![]() $Y$
is balanced at all primes, but the case where
$Y$
is balanced at all primes, but the case where
![]() $Y$
is merely balanced at prime divisors of
$Y$
is merely balanced at prime divisors of
![]() $a$
follows from its proof.
$a$
follows from its proof.
For every
![]() $j\in \{1,2,\ldots, \ell (d)\}$
, define a set of indices by
$j\in \{1,2,\ldots, \ell (d)\}$
, define a set of indices by
Then, for every
![]() $r \leq \ell (d)$
, the set of indices
$r \leq \ell (d)$
, the set of indices
![]() $i$
with
$i$
with
![]() $F(e_i)\notin G_r$
is given by
$F(e_i)\notin G_r$
is given by
![]() $\Sigma _r \,:\!=\, \cup _{j=1}^r \sigma _j$
. Write
$\Sigma _r \,:\!=\, \cup _{j=1}^r \sigma _j$
. Write
![]() $Y = (y_1,\ldots, y_n)$
and observe that
$Y = (y_1,\ldots, y_n)$
and observe that
![]() $\sum _{i\notin \Sigma _r} y_i F(e_i) \in G_r$
for any
$\sum _{i\notin \Sigma _r} y_i F(e_i) \in G_r$
for any
![]() $r \leq \ell (d)$
. Consequently, since
$r \leq \ell (d)$
. Consequently, since
![]() $F(Y) = \sum _{i=1}^n y_i F(e_i)$
, it is only possible to have
$F(Y) = \sum _{i=1}^n y_i F(e_i)$
, it is only possible to have
![]() $F(Y) = g$
if
$F(Y) = g$
if
![]() $\sum _{i\in \Sigma _r}y_i F(e_i) - g \in G_r$
for all
$\sum _{i\in \Sigma _r}y_i F(e_i) - g \in G_r$
for all
![]() $r \leq \ell (d)$
. Hence, by definition of conditional probability,
$r \leq \ell (d)$
. Hence, by definition of conditional probability,
 \begin{align}{\mathbb{P}}\left(F(Y) = g\right)&={\mathbb{P}}\left(\sum _{i\in \Sigma _1} y_i F(y_i) - g \in G_1\right){\mathbb{P}}\left(F(Y) = g\,\Big \vert \, \sum _{i\in \Sigma _1} y_i F(y_i) - g \in G_1 \right)\nonumber \\ &= \prod _{j=1}^{\ell (d)}{\mathbb{P}}\left(\sum _{i\in \Sigma _j} y_i F(y_i) - g \in G_j \,\Big \vert \, \forall r \lt j\,:\,\sum _{i\in \Sigma _r} y_i F(y_i) - g \in G_r\right) \\ &\quad \times{\mathbb{P}}\left(F(Y) = g\,\Big \vert \, \forall r \leq \ell (d)\,:\,\sum _{i\in \Sigma _r} y_i F(y_i) - g \in G_r \right). \nonumber \end{align}
\begin{align}{\mathbb{P}}\left(F(Y) = g\right)&={\mathbb{P}}\left(\sum _{i\in \Sigma _1} y_i F(y_i) - g \in G_1\right){\mathbb{P}}\left(F(Y) = g\,\Big \vert \, \sum _{i\in \Sigma _1} y_i F(y_i) - g \in G_1 \right)\nonumber \\ &= \prod _{j=1}^{\ell (d)}{\mathbb{P}}\left(\sum _{i\in \Sigma _j} y_i F(y_i) - g \in G_j \,\Big \vert \, \forall r \lt j\,:\,\sum _{i\in \Sigma _r} y_i F(y_i) - g \in G_r\right) \\ &\quad \times{\mathbb{P}}\left(F(Y) = g\,\Big \vert \, \forall r \leq \ell (d)\,:\,\sum _{i\in \Sigma _r} y_i F(y_i) - g \in G_r \right). \nonumber \end{align}
We next bound the probabilities occurring in (3.15). Recall that the
![]() $y_i$
are independent. Hence, if we fix some
$y_i$
are independent. Hence, if we fix some
![]() $j \leq \ell (d)$
and condition on the values achieved by the
$j \leq \ell (d)$
and condition on the values achieved by the
![]() $y_i$
with
$y_i$
with
![]() $i\in \Sigma _{j-1}$
, then
$i\in \Sigma _{j-1}$
, then
 \begin{align}{\mathbb{P}}&\left(\sum _{i\in \Sigma _{j}}y_i F(e_i) - g \in G_{j}\, \Big \vert \, \forall r \lt j\,:\,\sum _{i\in \Sigma _r} y_i F(y_i) - g \in G_r\right)\\ &={\mathbb{E}}\left[{\mathbb{P}}\Bigl (\sum _{i\in \Sigma _{j}}y_i F(e_i) - g \in G_{j}\, \Big \vert \, y_i \,:\, i\in \Sigma _{j-1}\Bigr ) \, \Big \vert \, \forall r \lt j\,:\,\sum _{i\in \Sigma _r} y_i F(y_i) - g \in G_r\right]\nonumber \\ &\leq \max _{h\in G_{j-1}}{\mathbb{P}}\left(\sum _{i\in \sigma _{j}}y_i F(e_i) - h \in G_{j}\right). \nonumber \end{align}
\begin{align}{\mathbb{P}}&\left(\sum _{i\in \Sigma _{j}}y_i F(e_i) - g \in G_{j}\, \Big \vert \, \forall r \lt j\,:\,\sum _{i\in \Sigma _r} y_i F(y_i) - g \in G_r\right)\\ &={\mathbb{E}}\left[{\mathbb{P}}\Bigl (\sum _{i\in \Sigma _{j}}y_i F(e_i) - g \in G_{j}\, \Big \vert \, y_i \,:\, i\in \Sigma _{j-1}\Bigr ) \, \Big \vert \, \forall r \lt j\,:\,\sum _{i\in \Sigma _r} y_i F(y_i) - g \in G_r\right]\nonumber \\ &\leq \max _{h\in G_{j-1}}{\mathbb{P}}\left(\sum _{i\in \sigma _{j}}y_i F(e_i) - h \in G_{j}\right). \nonumber \end{align}
Here, the final step used that
![]() $\Sigma _{j}\setminus \Sigma _{j-1} =\sigma _j$
, and
$\Sigma _{j}\setminus \Sigma _{j-1} =\sigma _j$
, and
![]() $\sum _{i\in \Sigma _{j-1}}y_i F(e_i) -g$
was identified with
$\sum _{i\in \Sigma _{j-1}}y_i F(e_i) -g$
was identified with
![]() $h$
. Denote
$h$
. Denote
![]() $F_{j}\,:\,V_{\sigma _{j}} \to G_{j-1}/G_j$
for the map found by restricting
$F_{j}\,:\,V_{\sigma _{j}} \to G_{j-1}/G_j$
for the map found by restricting
![]() $F$
to
$F$
to
![]() $V_{\sigma _j}$
and reducing modulo
$V_{\sigma _j}$
and reducing modulo
![]() $G_{j}$
. Recall (3.12) and note that
$G_{j}$
. Recall (3.12) and note that
![]() $w_j = \#\sigma _j$
. We claim that
$w_j = \#\sigma _j$
. We claim that
![]() $F_j$
is a code of distance
$F_j$
is a code of distance
![]() $w_j$
; recall Definition 3.5. Indeed, the maximality of (3.11) ensures that
$w_j$
; recall Definition 3.5. Indeed, the maximality of (3.11) ensures that
![]() $G_{j-1}/G_j$
is a cyclic group of prime order and consequently, for every
$G_{j-1}/G_j$
is a cyclic group of prime order and consequently, for every
![]() $i\in \sigma _j$
,
$i\in \sigma _j$
,
![]() $F_j(e_i)$
generates
$F_j(e_i)$
generates
![]() $G_{j-1}/G_j$
since
$G_{j-1}/G_j$
since
![]() $F_j(e_i) \not \equiv 0 \bmod G_j$
by definition of
$F_j(e_i) \not \equiv 0 \bmod G_j$
by definition of
![]() $\sigma _j$
; recall (3.14). Now apply [Reference Nguyen and Wood15, Lemma 4.5] to
$\sigma _j$
; recall (3.14). Now apply [Reference Nguyen and Wood15, Lemma 4.5] to
![]() $F_j$
and use that
$F_j$
and use that
![]() $p_j =\#(G_{j-1}/G_j)$
to find
$p_j =\#(G_{j-1}/G_j)$
to find
 \begin{align}{\mathbb{P}}\left(\sum _{i\in \sigma _{j}}y_i F(e_i) - h \in G_{j}\right) \leq \frac{1}{p_j} + \frac{p_j - 1}{p_j} \exp \left(-\frac{\alpha w_j}{p_j^2}\right). \end{align}
\begin{align}{\mathbb{P}}\left(\sum _{i\in \sigma _{j}}y_i F(e_i) - h \in G_{j}\right) \leq \frac{1}{p_j} + \frac{p_j - 1}{p_j} \exp \left(-\frac{\alpha w_j}{p_j^2}\right). \end{align}
Using this bound on the product in (3.15) yields the product in (3.13). It remains to bound the remaining factor. Here, similarly to (3.16), we have
 \begin{align*}{\mathbb{P}}\left(F(Y) = g\,\Big \vert \, \forall r \leq \ell (d)\,:\,\sum _{i\in \Sigma _r} y_i F(y_i) - g \in G_r \right) \leq \max _{h \in G_{\ell (d)}}{\mathbb{P}}\left(\sum _{i\not \in \Sigma _{\ell (d)}}y_i F(e_i) = h \right). \end{align*}
\begin{align*}{\mathbb{P}}\left(F(Y) = g\,\Big \vert \, \forall r \leq \ell (d)\,:\,\sum _{i\in \Sigma _r} y_i F(y_i) - g \in G_r \right) \leq \max _{h \in G_{\ell (d)}}{\mathbb{P}}\left(\sum _{i\not \in \Sigma _{\ell (d)}}y_i F(e_i) = h \right). \end{align*}
By the argument preceding (3.9), the restriction of
![]() $F$
to
$F$
to
![]() $V_{\setminus \Sigma _{\ell (d)}}$
defines a code of distance
$V_{\setminus \Sigma _{\ell (d)}}$
defines a code of distance
![]() $\delta n$
. Hence, by [Reference Nguyen and Wood15, Lemma 4.5] and the fact that
$\delta n$
. Hence, by [Reference Nguyen and Wood15, Lemma 4.5] and the fact that
![]() $\exp (H)\mid \exp (G)$
,
$\exp (H)\mid \exp (G)$
,
 \begin{align}{\mathbb{P}}\left(\sum _{i\not \in \Sigma _{\ell (d)}}y_i F(e_i) = h \right) \leq (\#H)^{-1} + \exp (-\alpha \delta n/a^2). \end{align}
\begin{align}{\mathbb{P}}\left(\sum _{i\not \in \Sigma _{\ell (d)}}y_i F(e_i) = h \right) \leq (\#H)^{-1} + \exp (-\alpha \delta n/a^2). \end{align}
It was here used that
![]() $(\#H -1)/\#H \leq 1$
. Use that
$(\#H -1)/\#H \leq 1$
. Use that
![]() $\# H = \#G/d$
to conclude the proof.
$\# H = \#G/d$
to conclude the proof.
Corollary 3.9.
Adopt assumption (A1), and let
![]() $N$
be a
$N$
be a
![]() ${\mathbb{Z}}[x]$
-module such that all prime divisors of
${\mathbb{Z}}[x]$
-module such that all prime divisors of
![]() $\#N$
are in
$\#N$
are in
![]() $\mathscr{P}$
. Then, for every subgroup
$\mathscr{P}$
. Then, for every subgroup
![]() $H\subseteq N$
and every
$H\subseteq N$
and every
![]() $F\in{\operatorname{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N)$
, which is
$F\in{\operatorname{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N)$
, which is
![]() $\delta$
-robust for
$\delta$
-robust for
![]() $H$
,
$H$
,
 \begin{align*}{\mathbb{P}}(F{\mathbf{X}} = xF) \leq & \left( (\#N)^{-1}d + \exp \left(-\alpha _n \delta n/a^2\right) \right)^n \prod _{j=1}^{\ell (d)}\left(p_j^{-1} + \frac{p_j -1}{p_j}\exp \left(-\alpha _n w_j/p_j^2\right) \right)^n \end{align*}
\begin{align*}{\mathbb{P}}(F{\mathbf{X}} = xF) \leq & \left( (\#N)^{-1}d + \exp \left(-\alpha _n \delta n/a^2\right) \right)^n \prod _{j=1}^{\ell (d)}\left(p_j^{-1} + \frac{p_j -1}{p_j}\exp \left(-\alpha _n w_j/p_j^2\right) \right)^n \end{align*}
where
![]() $d,p_j,w_j$
, and
$d,p_j,w_j$
, and
![]() $a$
are defined as in Lemma 3.8 with
$a$
are defined as in Lemma 3.8 with
![]() $G = N$
.
$G = N$
.
Proof. Since the entries of
![]() $\mathbf{X}$
are assumed to be independent, one has that
$\mathbf{X}$
are assumed to be independent, one has that
![]() ${\mathbb{P}}(F{\mathbf{X}} = xF) = \prod _{i=1}^n{\mathbb{P}}(F({\mathbf{X}} e_i) = xF(e_i))$
. The result is hence immediate from Lemma 3.8 applied with
${\mathbb{P}}(F{\mathbf{X}} = xF) = \prod _{i=1}^n{\mathbb{P}}(F({\mathbf{X}} e_i) = xF(e_i))$
. The result is hence immediate from Lemma 3.8 applied with
![]() $Y \,:\!=\,{\mathbf{X}} e_i$
and
$Y \,:\!=\,{\mathbf{X}} e_i$
and
![]() $g \,:\!=\, xF(e_i)$
.
$g \,:\!=\, xF(e_i)$
.
Lemma 3.10.
Let
![]() $N$
be a
$N$
be a
![]() ${\mathbb{Z}}[x]$
-module such that all prime divisors of
${\mathbb{Z}}[x]$
-module such that all prime divisors of
![]() $\#N$
are in
$\#N$
are in
![]() $\mathscr{P}$
and adopt assumptions 1 and 3. Then, there exists
$\mathscr{P}$
and adopt assumptions 1 and 3. Then, there exists
![]() $\delta _0 \gt 0$
such that for every
$\delta _0 \gt 0$
such that for every
![]() $\delta \lt \delta _0$
, there exist constants
$\delta \lt \delta _0$
, there exist constants
![]() $C,c \gt 0$
such that for all
$C,c \gt 0$
such that for all
![]() $n\geq 1$
$n\geq 1$
 \begin{align*} \sum _{\substack{F\in \operatorname{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) \\ F\text{ not a code of distance }\delta n}}{\mathbb{P}}(F{\mathbf{X}} = xF) \leq C n^{-c}. \end{align*}
\begin{align*} \sum _{\substack{F\in \operatorname{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) \\ F\text{ not a code of distance }\delta n}}{\mathbb{P}}(F{\mathbf{X}} = xF) \leq C n^{-c}. \end{align*}
Proof. By (3.10), one may upper bound the sum as
 \begin{align} \sum _{\substack{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) \\ F\text{ not a code of distance }\delta n}}{\mathbb{P}}(F{\mathbf{X}} = xF) \leq \sum _{H\subsetneq N}\sum _{\substack{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) \\ F\text{ is }\delta \text{-robust for }H}}{\mathbb{P}}(F{\mathbf{X}} = xF). \end{align}
\begin{align} \sum _{\substack{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) \\ F\text{ not a code of distance }\delta n}}{\mathbb{P}}(F{\mathbf{X}} = xF) \leq \sum _{H\subsetneq N}\sum _{\substack{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) \\ F\text{ is }\delta \text{-robust for }H}}{\mathbb{P}}(F{\mathbf{X}} = xF). \end{align}
Fix some proper subgroup
![]() $H\subsetneq N$
and pick a maximal chain of subgroups
$H\subsetneq N$
and pick a maximal chain of subgroups
![]() $G_j$
as in (3.11) with
$G_j$
as in (3.11) with
![]() $G=N$
. We denote
$G=N$
. We denote
![]() $d \,:\!=\, [N\,:\,H]$
.
$d \,:\!=\, [N\,:\,H]$
.
By [Reference Nguyen and Wood15, Lemma 4.10], the number of
![]() $F\in{\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N)$
that are
$F\in{\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N)$
that are
![]() $\delta$
-robust for
$\delta$
-robust for
![]() $H$
and satisfy that there are exactly
$H$
and satisfy that there are exactly
![]() $w_j$
indices
$w_j$
indices
![]() $i\leq n$
with
$i\leq n$
with
![]() $F(e_i) \in G_{j-1}\setminus G_j$
for
$F(e_i) \in G_{j-1}\setminus G_j$
for
![]() $1 \leq j \leq \ell (d)$
is at most
$1 \leq j \leq \ell (d)$
is at most
![]() $(\# H)^{n-\sum _{j=1}^{\ell (d)}w_j} \prod _{j=1}^{\ell (d)} \binom{n}{w_j}(\# G_{j-1})^{w_j}$
. When
$(\# H)^{n-\sum _{j=1}^{\ell (d)}w_j} \prod _{j=1}^{\ell (d)} \binom{n}{w_j}(\# G_{j-1})^{w_j}$
. When
![]() $F$
is surjective, we have
$F$
is surjective, we have
![]() $w_1 \neq 0$
. Further, when
$w_1 \neq 0$
. Further, when
![]() $F$
is
$F$
is
![]() $\delta$
-robust for
$\delta$
-robust for
![]() $H$
, we have
$H$
, we have
![]() $w_j \leq \ell (d) \delta n$
for all
$w_j \leq \ell (d) \delta n$
for all
![]() $j\leq \ell (d)$
. Indeed, if this were not the case, then we would have
$j\leq \ell (d)$
. Indeed, if this were not the case, then we would have
![]() $\#\{i\leq n\,:\, F(e_i) \not \in H \} \gt \ell (d)\delta n$
, which contradicts (3.8). Now, by the combination of Corollary 3.9 with the aforementioned count on the number of
$\#\{i\leq n\,:\, F(e_i) \not \in H \} \gt \ell (d)\delta n$
, which contradicts (3.8). Now, by the combination of Corollary 3.9 with the aforementioned count on the number of
![]() $\delta$
-robust morphisms,
$\delta$
-robust morphisms,
 \begin{align} \sum _{\substack{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) \\ F\text{ is }\delta \text{-robust for }H}}&{\mathbb{P}}(F{\mathbf{X}} = xF)\leq \sum _{\substack{0 \leq w_1,\ldots, w_{\ell (d)}\leq \ell (d) \delta n\\ w_1 \neq 0} } (\#H)^{n-\sum _{j=1}^{\ell (d)}w_j} \prod _{j=1}^{\ell (d)} \binom{n}{w_j}(\# G_{j-1})^{w_j} \\ &\times \left( (\#N)^{-1}d + \exp \left(-\alpha _n \delta n/a^2\right) \right)^n \prod _{j=1}^{\ell (d)}\left(p_j^{-1} + \frac{p_j -1}{p_j}\exp \left(-\alpha _n w_j/p_j^2\right) \right)^n.\nonumber \end{align}
\begin{align} \sum _{\substack{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) \\ F\text{ is }\delta \text{-robust for }H}}&{\mathbb{P}}(F{\mathbf{X}} = xF)\leq \sum _{\substack{0 \leq w_1,\ldots, w_{\ell (d)}\leq \ell (d) \delta n\\ w_1 \neq 0} } (\#H)^{n-\sum _{j=1}^{\ell (d)}w_j} \prod _{j=1}^{\ell (d)} \binom{n}{w_j}(\# G_{j-1})^{w_j} \\ &\times \left( (\#N)^{-1}d + \exp \left(-\alpha _n \delta n/a^2\right) \right)^n \prod _{j=1}^{\ell (d)}\left(p_j^{-1} + \frac{p_j -1}{p_j}\exp \left(-\alpha _n w_j/p_j^2\right) \right)^n.\nonumber \end{align}
It remains a nontrivial task to compute the right-hand side of (3.20). Fortunately, a related sum was considered by Nguyen and Wood [Reference Nguyen and Wood15], and we can extract the relevant estimate from their proofs. More precisely, the sum in (3.20) is a special case of the sum which occurs in the first centred equation of the proof of [Reference Nguyen and Wood15, Theorem 4.12]: take
![]() $u=0$
in their notation. Following the arguments word for word up to the centred inequality at the end of page 23 in [Reference Nguyen and Wood15] now yields the desired result.
$u=0$
in their notation. Following the arguments word for word up to the centred inequality at the end of page 23 in [Reference Nguyen and Wood15] now yields the desired result.
Lemma 3.11.
Adopt assumptions (A1) and (A3), and fix a
![]() ${\mathbb{Z}}[x]$
-module
${\mathbb{Z}}[x]$
-module
![]() $N$
such that all prime divisors of
$N$
such that all prime divisors of
![]() $\#N$
are in
$\#N$
are in
![]() $\mathscr{P}$
. Then, there exists
$\mathscr{P}$
. Then, there exists
![]() $\delta _0 \gt 0$
such that for every
$\delta _0 \gt 0$
such that for every
![]() $\delta \lt \delta _0$
, there exist constants
$\delta \lt \delta _0$
, there exist constants
![]() $C,c \gt 0$
such that for all
$C,c \gt 0$
such that for all
![]() $n\geq 1$
$n\geq 1$
 \begin{align*} \sum _{\substack{F\in \operatorname{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) \\ F\text{ not a code of distance }\delta n}} \lvert{\mathbb{P}}(F{\mathbf{X}} = xF) - (\#N)^{-n} \rvert \leq C n^{-c}. \end{align*}
\begin{align*} \sum _{\substack{F\in \operatorname{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) \\ F\text{ not a code of distance }\delta n}} \lvert{\mathbb{P}}(F{\mathbf{X}} = xF) - (\#N)^{-n} \rvert \leq C n^{-c}. \end{align*}
Proof. By Definition 3.5, if
![]() $F$
is not a code of distance
$F$
is not a code of distance
![]() $\delta n$
, then we can find some
$\delta n$
, then we can find some
![]() $\sigma \subseteq \{1,\ldots, n \}$
and a proper subgroup
$\sigma \subseteq \{1,\ldots, n \}$
and a proper subgroup
![]() $H \subsetneq N$
such that
$H \subsetneq N$
such that
![]() $F(V_{\setminus \sigma }) \subseteq H$
and
$F(V_{\setminus \sigma }) \subseteq H$
and
![]() $\# \sigma = \lfloor \delta n \rfloor$
. Hence, since
$\# \sigma = \lfloor \delta n \rfloor$
. Hence, since
![]() $F$
is uniquely determined by the images of the basis elements of
$F$
is uniquely determined by the images of the basis elements of
![]() ${\mathbb{Z}}^n$
,
${\mathbb{Z}}^n$
,
 \begin{align} \sum _{\substack{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) \\ F\text{ not a code of distance }\delta n}} (\#N)^{-n} \leq \sum _{H \subsetneq N} \binom{n}{\lfloor \delta n\rfloor } (\# H)^{n - \lfloor \delta n \rfloor } (\# N)^{-n + \lfloor \delta n \rfloor }. \end{align}
\begin{align} \sum _{\substack{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) \\ F\text{ not a code of distance }\delta n}} (\#N)^{-n} \leq \sum _{H \subsetneq N} \binom{n}{\lfloor \delta n\rfloor } (\# H)^{n - \lfloor \delta n \rfloor } (\# N)^{-n + \lfloor \delta n \rfloor }. \end{align}
The binary entropy bound [Reference Cover and Thomas6, Eq.(7.14), p. 151] implies that
![]() $\binom{n}{\lfloor \delta n\rfloor } \leq 2^{n E(\lfloor \delta n \rfloor /n)}$
where
$\binom{n}{\lfloor \delta n\rfloor } \leq 2^{n E(\lfloor \delta n \rfloor /n)}$
where
![]() $E(y)\,:\!=\, -y\log _2(y) + (1-y)\log _2(1-y)$
. Note that
$E(y)\,:\!=\, -y\log _2(y) + (1-y)\log _2(1-y)$
. Note that
![]() $\lim _{y \to 0} E(y) = 0$
. We can hence find some sufficiently small
$\lim _{y \to 0} E(y) = 0$
. We can hence find some sufficiently small
![]() $\delta _0$
such that Lemma 3.10 is applicable and
$\delta _0$
such that Lemma 3.10 is applicable and
![]() $\delta _0 + E(\lfloor \delta _0 n \rfloor /n) \lt 1/2$
for all
$\delta _0 + E(\lfloor \delta _0 n \rfloor /n) \lt 1/2$
for all
![]() $n\geq 1$
. Then, since
$n\geq 1$
. Then, since
![]() $\#H \leq \#N /2$
, we have for every
$\#H \leq \#N /2$
, we have for every
![]() $\delta \lt \delta _0$
that
$\delta \lt \delta _0$
that
 \begin{align} \sum _{\substack{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) \\ F\text{ not a code of distance }\delta n}} (\#N)^{-n} \leq S_N 2^{(E(\lfloor \delta n\rfloor /n ) + \delta - 1)n} \leq S_N 2^{-n/2} \end{align}
\begin{align} \sum _{\substack{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) \\ F\text{ not a code of distance }\delta n}} (\#N)^{-n} \leq S_N 2^{(E(\lfloor \delta n\rfloor /n ) + \delta - 1)n} \leq S_N 2^{-n/2} \end{align}
where
![]() $S_N$
is the number of proper subgroups of
$S_N$
is the number of proper subgroups of
![]() $N$
. Let
$N$
. Let
![]() $C^{\prime},c^{\prime}\gt 0$
be such that
$C^{\prime},c^{\prime}\gt 0$
be such that
![]() $S_N 2^{-n/2} \leq C^{\prime} n^{-c^{\prime}}$
for all
$S_N 2^{-n/2} \leq C^{\prime} n^{-c^{\prime}}$
for all
![]() $n\geq 1$
, and use Lemma 3.10 together with the triangle inequality to conclude the proof.
$n\geq 1$
, and use Lemma 3.10 together with the triangle inequality to conclude the proof.
3.1.4. Combining the estimates
We finally combine all preceding estimates to complete the proof of Proposition 3.1.
Proof of Proposition 3.1. By (3.3) and the triangle inequality,
 \begin{align} \lvert{\mathbb{E}}[\#\textrm{Sur}_{{\mathbb{Z}}[x]}(\textrm{coker}(\tilde{{\mathbf{W}}}),N)] - (\#{}&{} N)^{-k} \rvert \leq \sum _{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N)\,:\, F{\mathbf{B}} = 0}\left \lvert (\#N)^{-n} -{\mathbb{P}}(F{\mathbf{X}} = xF) \right \rvert \\ &\quad +\left \lvert (\# N)^{-n}\#\{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N)\,:\, F{\mathbf{B}} = 0\}- (\# N)^{-k} \right \rvert . \nonumber \end{align}
\begin{align} \lvert{\mathbb{E}}[\#\textrm{Sur}_{{\mathbb{Z}}[x]}(\textrm{coker}(\tilde{{\mathbf{W}}}),N)] - (\#{}&{} N)^{-k} \rvert \leq \sum _{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N)\,:\, F{\mathbf{B}} = 0}\left \lvert (\#N)^{-n} -{\mathbb{P}}(F{\mathbf{X}} = xF) \right \rvert \\ &\quad +\left \lvert (\# N)^{-n}\#\{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N)\,:\, F{\mathbf{B}} = 0\}- (\# N)^{-k} \right \rvert . \nonumber \end{align}
Pick some
![]() $\delta \gt 0$
, which is sufficiently small to ensure that Lemma 3.11 is applicable. Then, by the triangle inequality,
$\delta \gt 0$
, which is sufficiently small to ensure that Lemma 3.11 is applicable. Then, by the triangle inequality,
 \begin{align} &\sum _{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N)\,:\, F{\mathbf{B}} = 0}\lvert (\#N)^{-n} -{\mathbb{P}}(F{\mathbf{X}} = xF) \rvert \\ &\quad \leq \sum _{\substack{F\in{\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) \\ F\text{ a code of distance }\delta n}} \lvert (\#N)^{-n} -{\mathbb{P}}(F{\mathbf{X}} = xF) \rvert + \sum _{\substack{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) \\ F\text{ not a code of distance }\delta n}} \lvert (\#N)^{-n} -{\mathbb{P}}(F{\mathbf{X}} = xF)\rvert .\nonumber \end{align}
\begin{align} &\sum _{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N)\,:\, F{\mathbf{B}} = 0}\lvert (\#N)^{-n} -{\mathbb{P}}(F{\mathbf{X}} = xF) \rvert \\ &\quad \leq \sum _{\substack{F\in{\textrm{Hom}}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) \\ F\text{ a code of distance }\delta n}} \lvert (\#N)^{-n} -{\mathbb{P}}(F{\mathbf{X}} = xF) \rvert + \sum _{\substack{F\in \textrm{Sur}_{{\mathbb{Z}}}({\mathbb{Z}}^n,N) \\ F\text{ not a code of distance }\delta n}} \lvert (\#N)^{-n} -{\mathbb{P}}(F{\mathbf{X}} = xF)\rvert .\nonumber \end{align}
Let
![]() $c,C\gt$
be the constants from Lemma 3.6, and let
$c,C\gt$
be the constants from Lemma 3.6, and let
![]() $c^{\prime},C^{\prime}\gt 0$
be the constants from Lemma 3.11. Then, the right-hand side of (3.24) is at most
$c^{\prime},C^{\prime}\gt 0$
be the constants from Lemma 3.11. Then, the right-hand side of (3.24) is at most
![]() $Cn^{-c} + C^{\prime}n^{-c^{\prime}}$
and hence tends to zero as
$Cn^{-c} + C^{\prime}n^{-c^{\prime}}$
and hence tends to zero as
![]() $n$
tends to infinity. Further, by Lemma 3.4, there exists a constant
$n$
tends to infinity. Further, by Lemma 3.4, there exists a constant
![]() $C^{\prime\prime}\gt 0$
such that
$C^{\prime\prime}\gt 0$
such that
Remark that the right-hand side of (3.25) tends to zero as
![]() $n$
tends to infinity to conclude the proof.
$n$
tends to infinity to conclude the proof.
3.2 Solving the moment problem
We next apply a general result concerning measures on categories of [Reference Sawin and Wood20, Theorem 1.6] to invert the moment problem. Using [Reference Sawin and Wood20, Lemma 6.1] and [Reference Sawin and Wood20, Lemma 6.3], that result may be specialised to our context – namely, to limiting measures on the category of finite modules with
![]() $N$
-moments given by
$N$
-moments given by
![]() $(\#N)^{-k}$
. Let us state this specialisation explicitly for the sake of definiteness:
$(\#N)^{-k}$
. Let us state this specialisation explicitly for the sake of definiteness:
Lemma 3.12 (Special case of [Reference Sawin and Wood20, Theorem 1.6]). Let
![]() $R$
be a ring and consider a sequence of random finite
$R$
be a ring and consider a sequence of random finite
![]() $R$
-modules
$R$
-modules
![]() $X_{n}$
such that for every fixed finite
$X_{n}$
such that for every fixed finite
![]() $R$
-module
$R$
-module
![]() $N$
$N$
Let
![]() $S$
be quotient ring of
$S$
be quotient ring of
![]() $R$
with
$R$
with
![]() $\#S \lt \infty$
, and let
$\#S \lt \infty$
, and let
![]() $L_1,\ldots, L_r$
be representatives of the isomorphism classes of finite simple
$L_1,\ldots, L_r$
be representatives of the isomorphism classes of finite simple
![]() $S$
-modules. Further, denote
$S$
-modules. Further, denote
![]() $q_i$
for the cardinality of the endomorphism field of
$q_i$
for the cardinality of the endomorphism field of
![]() $L_i$
for every
$L_i$
for every
![]() $i\leq r$
. Then, for every finite
$i\leq r$
. Then, for every finite
![]() $S$
-module
$S$
-module
![]() $N$
,
$N$
,
 \begin{align*} \lim _{n\to \infty }{\mathbb{P}}(X_n\otimes _{R}S \cong N) &= \frac{1}{ (\# N)^k\#{\operatorname{Aut}}_S(N)} \prod _{i=1}^r \prod _{j=1}^\infty \left(1 - \frac{q_i^{-j}\#\operatorname{Ext}^1_S(N,L_i) }{\#{\operatorname{Hom}}_{S}(N,L_i) (\# L_i)^k} \right). \end{align*}
\begin{align*} \lim _{n\to \infty }{\mathbb{P}}(X_n\otimes _{R}S \cong N) &= \frac{1}{ (\# N)^k\#{\operatorname{Aut}}_S(N)} \prod _{i=1}^r \prod _{j=1}^\infty \left(1 - \frac{q_i^{-j}\#\operatorname{Ext}^1_S(N,L_i) }{\#{\operatorname{Hom}}_{S}(N,L_i) (\# L_i)^k} \right). \end{align*}
Let us further remark that it follows from the statement of [Reference Sawin and Wood20, Theorem 1.6] that the limiting measure in Lemma 3.12 has
![]() $N$
-moments given by
$N$
-moments given by
![]() $(\#N)^{-k}$
. In particular, the
$(\#N)^{-k}$
. In particular, the
![]() $N$
-moment for
$N$
-moment for
![]() $N = \{0 \}$
is equal to one, which implies that the limiting measure is a probability measure.
$N = \{0 \}$
is equal to one, which implies that the limiting measure is a probability measure.
It now remains to combine Proposition 3.1 with Lemma 3.12 and to simplify the results. This can be accomplished with a direct computation. Note that the following result implies Theorem 1.3 as the special case with
![]() $k=1$
.
$k=1$
.
Proposition 3.13.
Adopt assumptions (A1)to (A3). Fix a positive integer
![]() $m\geq 1$
, a monic polynomial
$m\geq 1$
, a monic polynomial
![]() $Q\in{\mathbb{Z}}[x]$
of degree
$Q\in{\mathbb{Z}}[x]$
of degree
![]() $\geq 1$
, and introduce
$\geq 1$
, and introduce
![]() $Q_{i,p}\in{\mathbb{F}}_p[x]$
,
$Q_{i,p}\in{\mathbb{F}}_p[x]$
,
![]() $r_p\geq 1$
, and
$r_p\geq 1$
, and
![]() $d_{i,p} = \deg Q_{i,p}$
using the factorisation of
$d_{i,p} = \deg Q_{i,p}$
using the factorisation of
![]() $Q$
modulo
$Q$
modulo
![]() $p$
as in Theorem
1.3
.
$p$
as in Theorem
1.3
.
For every
![]() $p\in \mathscr{P}$
, denote
$p\in \mathscr{P}$
, denote
![]() $S_{p^m} \,:\!=\,{\mathbb{Z}}[x]/( p^m{\mathbb{Z}}[x] + Q(x){\mathbb{Z}}[x] )$
. Then, given a finite
$S_{p^m} \,:\!=\,{\mathbb{Z}}[x]/( p^m{\mathbb{Z}}[x] + Q(x){\mathbb{Z}}[x] )$
. Then, given a finite
![]() $S_{p^m}$
-module
$S_{p^m}$
-module
![]() $N_{p^m, Q}$
for every
$N_{p^m, Q}$
for every
![]() $p\in \mathscr{P}$
, it holds that
$p\in \mathscr{P}$
, it holds that
 \begin{align*} \lim _{n\to \infty }{\mathbb{P}}(\forall p\in \mathscr{P}\,:\,&{\operatorname{coker}}(\tilde{{\mathbf{W}}})_{p^m,Q} \cong N_{p^m,Q}) = \prod _{p\in \mathscr{P}}\left( \frac{1}{(\#N_{p^m,Q})^k\#{\operatorname{Aut}}_{S_{p^m}}(N_{p^m,Q})}\right.\\ &\quad \left.\times \prod _{i = 1}^{r_p} \prod _{j=1}^\infty \left(1-\frac{\#\operatorname{Ext}_{S_{p^m}}^1\bigl (N_{p^m,Q},{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x]) \bigr )}{\#{\operatorname{Hom}}_{S_{p^m}}\bigl (N_{p^m,Q},{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x]) \bigr )} p^{-(k+j)d_{i,p} } \right)\right). \end{align*}
\begin{align*} \lim _{n\to \infty }{\mathbb{P}}(\forall p\in \mathscr{P}\,:\,&{\operatorname{coker}}(\tilde{{\mathbf{W}}})_{p^m,Q} \cong N_{p^m,Q}) = \prod _{p\in \mathscr{P}}\left( \frac{1}{(\#N_{p^m,Q})^k\#{\operatorname{Aut}}_{S_{p^m}}(N_{p^m,Q})}\right.\\ &\quad \left.\times \prod _{i = 1}^{r_p} \prod _{j=1}^\infty \left(1-\frac{\#\operatorname{Ext}_{S_{p^m}}^1\bigl (N_{p^m,Q},{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x]) \bigr )}{\#{\operatorname{Hom}}_{S_{p^m}}\bigl (N_{p^m,Q},{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x]) \bigr )} p^{-(k+j)d_{i,p} } \right)\right). \end{align*}
Proof. Denote
![]() $R \,:\!=\,{\mathbb{Z}}[x]/\left(\left(\prod _{p\in \mathscr{P}} p^m\right){\mathbb{Z}}[x]\right)$
and note that for any
$R \,:\!=\,{\mathbb{Z}}[x]/\left(\left(\prod _{p\in \mathscr{P}} p^m\right){\mathbb{Z}}[x]\right)$
and note that for any
![]() ${\mathbb{Z}}[x]$
-module
${\mathbb{Z}}[x]$
-module
![]() $M$
and any
$M$
and any
![]() $R$
-module
$R$
-module
![]() $N$
, one has a bijection between
$N$
, one has a bijection between
![]() $\textrm{Sur}_{R}(M\otimes _{{\mathbb{Z}}[x]}R,N)$
and
$\textrm{Sur}_{R}(M\otimes _{{\mathbb{Z}}[x]}R,N)$
and
![]() $\textrm{Sur}_{{\mathbb{Z}}[x]}(M, N)$
. Consequently, by Proposition 3.1, we have that for every finite
$\textrm{Sur}_{{\mathbb{Z}}[x]}(M, N)$
. Consequently, by Proposition 3.1, we have that for every finite
![]() $R$
-module
$R$
-module
![]() $N$
$N$
Let
![]() $S\,:\!=\, R/(Q(t)R)$
and define a finite
$S\,:\!=\, R/(Q(t)R)$
and define a finite
![]() $S$
-module by
$S$
-module by
![]() $N \,:\!=\, \oplus _{p\in \mathscr{P}} N_{p^m,Q}$
. The Chinese remainder theorem yields
$N \,:\!=\, \oplus _{p\in \mathscr{P}} N_{p^m,Q}$
. The Chinese remainder theorem yields
![]() $R \cong \oplus _{p\in \mathscr{P}}{\mathbb{Z}}[x]/(p^m{\mathbb{Z}}[x])$
, which implies that
$R \cong \oplus _{p\in \mathscr{P}}{\mathbb{Z}}[x]/(p^m{\mathbb{Z}}[x])$
, which implies that
![]() $S = \oplus _{p\in \mathscr{P}}S_{p^m}$
and
$S = \oplus _{p\in \mathscr{P}}S_{p^m}$
and
![]() $\textrm{coker}(\tilde{{\mathbf{W}}})\otimes _{{\mathbb{Z}}[x]}S \cong \oplus _{p\in \mathscr{P}} \textrm{coker}(\tilde{{\mathbf{W}}})_{p^m, Q}$
. Consequently, by Lemma 3.12 and the fact that isomorphism occurs if and only if the corresponding summands are isomorphic,
$\textrm{coker}(\tilde{{\mathbf{W}}})\otimes _{{\mathbb{Z}}[x]}S \cong \oplus _{p\in \mathscr{P}} \textrm{coker}(\tilde{{\mathbf{W}}})_{p^m, Q}$
. Consequently, by Lemma 3.12 and the fact that isomorphism occurs if and only if the corresponding summands are isomorphic,
 \begin{align} \lim _{n\to \infty }{\mathbb{P}}\bigl (\forall p\in \mathscr{P}\,:\,&\textrm{coker}(\tilde{{\mathbf{W}}})_{p^m,Q} \cong N_{p^m,Q}\bigr ) = \lim _{n\to \infty }{\mathbb{P}}\bigl ((\textrm{coker}(\tilde{{\mathbf{W}}})\otimes _{{\mathbb{Z}}[x]} R) \otimes _{R} S \cong N\bigr )\nonumber \\ &\ = \frac{1}{(\# N)^k\#{\textrm{Aut}}_S(N) } \prod _{i=1}^r \prod _{j=1}^\infty \left(1 - \frac{\#\textrm{Ext}^1_S(N,L_i) }{\#{\textrm{Hom}}_{S}(N,L_i) (\# L_i)^k}q_i^{-j} \right). \end{align}
\begin{align} \lim _{n\to \infty }{\mathbb{P}}\bigl (\forall p\in \mathscr{P}\,:\,&\textrm{coker}(\tilde{{\mathbf{W}}})_{p^m,Q} \cong N_{p^m,Q}\bigr ) = \lim _{n\to \infty }{\mathbb{P}}\bigl ((\textrm{coker}(\tilde{{\mathbf{W}}})\otimes _{{\mathbb{Z}}[x]} R) \otimes _{R} S \cong N\bigr )\nonumber \\ &\ = \frac{1}{(\# N)^k\#{\textrm{Aut}}_S(N) } \prod _{i=1}^r \prod _{j=1}^\infty \left(1 - \frac{\#\textrm{Ext}^1_S(N,L_i) }{\#{\textrm{Hom}}_{S}(N,L_i) (\# L_i)^k}q_i^{-j} \right). \end{align}
Simple modules over
![]() $S$
are precisely the modules of the form
$S$
are precisely the modules of the form
![]() $S/m$
with
$S/m$
with
![]() $m$
a maximal ideal of
$m$
a maximal ideal of
![]() $S$
. Further, maximal ideals of
$S$
. Further, maximal ideals of
![]() ${\mathbb{Z}}[x]$
are of the form
${\mathbb{Z}}[x]$
are of the form
![]() $m = p{\mathbb{Z}}[x] + f(x){\mathbb{Z}}[x]$
with
$m = p{\mathbb{Z}}[x] + f(x){\mathbb{Z}}[x]$
with
![]() $p$
a prime and
$p$
a prime and
![]() $f(x)\in{\mathbb{Z}}[x]$
irreducible modulo
$f(x)\in{\mathbb{Z}}[x]$
irreducible modulo
![]() $p$
of degree
$p$
of degree
![]() $\geq 1$
[Reference Reid19, p. 22]. Hence, since maximal ideals of
$\geq 1$
[Reference Reid19, p. 22]. Hence, since maximal ideals of
![]() $S$
are in one-to-one correspondence with maximal ideals of
$S$
are in one-to-one correspondence with maximal ideals of
![]() ${\mathbb{Z}}[x]$
, which contain
${\mathbb{Z}}[x]$
, which contain
![]() $\prod _{p\in \mathscr{P}}p^m$
and
$\prod _{p\in \mathscr{P}}p^m$
and
![]() $Q$
, the modules
$Q$
, the modules
![]() $L_i$
in (3.27) are of the form
$L_i$
in (3.27) are of the form
![]() ${\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x])$
. Consequently, by (3.27) and the fact that the endomorphism field of
${\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x])$
. Consequently, by (3.27) and the fact that the endomorphism field of
![]() ${\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x]))$
is isomorphic to
${\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x]))$
is isomorphic to
![]() ${\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x])$
, which is a finite field of order
${\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x])$
, which is a finite field of order
![]() $p^{d_{i,p}}$
,
$p^{d_{i,p}}$
,
 \begin{align} &\lim _{n\to \infty }{\mathbb{P}}\bigl (\forall p\in \mathscr{P}\,:\,\textrm{coker}(\tilde{{\mathbf{W}}})_{p^m,Q} \cong N_{p^m,Q}\bigr ) \\ &= \frac{1}{(\#N)^k\#{\textrm{Aut}}_{S}(N)}\prod _{p\in \mathscr{P}} \prod _{i = 1}^{r_p} \prod _{j=1}^\infty \left(1-\frac{\#\textrm{Ext}_{S}^1\bigl (N,{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x]) \bigr )}{\#{\textrm{Hom}}_{S}\bigl (N,{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x]) \bigr )} p^{-(k+j)d_{i,p} } \right). \nonumber \end{align}
\begin{align} &\lim _{n\to \infty }{\mathbb{P}}\bigl (\forall p\in \mathscr{P}\,:\,\textrm{coker}(\tilde{{\mathbf{W}}})_{p^m,Q} \cong N_{p^m,Q}\bigr ) \\ &= \frac{1}{(\#N)^k\#{\textrm{Aut}}_{S}(N)}\prod _{p\in \mathscr{P}} \prod _{i = 1}^{r_p} \prod _{j=1}^\infty \left(1-\frac{\#\textrm{Ext}_{S}^1\bigl (N,{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x]) \bigr )}{\#{\textrm{Hom}}_{S}\bigl (N,{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x]) \bigr )} p^{-(k+j)d_{i,p} } \right). \nonumber \end{align}
Here, observe that
![]() $\#N = \prod _{p\in \mathscr{P}} \#N_{p^m,Q}$
,
$\#N = \prod _{p\in \mathscr{P}} \#N_{p^m,Q}$
,
![]() $\#{\textrm{Aut}}_S(N)=\prod _{p\in \mathscr{P}}\#{\textrm{Aut}}_{S_{p^m}}(N_{p^m,Q})$
, and note that
$\#{\textrm{Aut}}_S(N)=\prod _{p\in \mathscr{P}}\#{\textrm{Aut}}_{S_{p^m}}(N_{p^m,Q})$
, and note that
![]() $\#{\textrm{Hom}}_{S}\bigl (N,{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x]) \bigr ) = \#{\textrm{Hom}}_{S_{p^m}}(N_{p^m,Q},{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x]))$
. Further, since
$\#{\textrm{Hom}}_{S}\bigl (N,{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x]) \bigr ) = \#{\textrm{Hom}}_{S_{p^m}}(N_{p^m,Q},{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x]))$
. Further, since
![]() $\textrm{Ext}$
takes direct sums in the first argument to products [Reference Weibel31, Proposition 3.3.4],
$\textrm{Ext}$
takes direct sums in the first argument to products [Reference Weibel31, Proposition 3.3.4],
Finally, using the definition of
![]() $\textrm{Ext}^1$
in terms of short exact sequences [Reference Weibel31, Theorem 3.4.3] together with the fact that finite
$\textrm{Ext}^1$
in terms of short exact sequences [Reference Weibel31, Theorem 3.4.3] together with the fact that finite
![]() $S$
-modules correspond to tuples of
$S$
-modules correspond to tuples of
![]() $S_{p^m}$
-modules, one can verify that
$S_{p^m}$
-modules, one can verify that
 \begin{align} \#\textrm{Ext}_{S}^1(N_{q^m,Q},{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x])) &= \begin{cases} \#\textrm{Ext}_{S_{p^m}}^1(N_{p^m,Q},{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x])) & \text{if }p=q,\\ 1 & \text{else}. \end{cases} \end{align}
\begin{align} \#\textrm{Ext}_{S}^1(N_{q^m,Q},{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x])) &= \begin{cases} \#\textrm{Ext}_{S_{p^m}}^1(N_{p^m,Q},{\mathbb{F}}_p[x]/(Q_{i,p}(x){\mathbb{F}}_p[x])) & \text{if }p=q,\\ 1 & \text{else}. \end{cases} \end{align}
4. Future work
Ultimately, we would like to show that the conditions of Theorem 1.1 are satisfied with nonvanishing probability. The current paper makes progress in this direction: we now have concrete proof techniques that can be used to study cokernels of walk matrices. There are however still a number of interesting open problems.
For instance, it remains entirely open to understand whether the condition
![]() $\textrm{coker}({\mathbf{W}})_{2^2} \cong ({\mathbb{Z}}/2{\mathbb{Z}})^{\lfloor n/2\rfloor }$
is often satisfied, even heuristically. This is because the distribution of
$\textrm{coker}({\mathbf{W}})_{2^2} \cong ({\mathbb{Z}}/2{\mathbb{Z}})^{\lfloor n/2\rfloor }$
is often satisfied, even heuristically. This is because the distribution of
![]() $\textrm{coker}({\mathbf{W}})_{2^m}$
is highly sensitive to the graph being simple, which makes approximation by results for directed graphs inadequate. Indeed, when
$\textrm{coker}({\mathbf{W}})_{2^m}$
is highly sensitive to the graph being simple, which makes approximation by results for directed graphs inadequate. Indeed, when
![]() $\mathbf{X}$
is the adjacency matrix of a simple graph and
$\mathbf{X}$
is the adjacency matrix of a simple graph and
![]() $b=e$
is the all-ones vector, then [Reference Wang26, Lemma 14] implies that
$b=e$
is the all-ones vector, then [Reference Wang26, Lemma 14] implies that
![]() ${\textrm{rank}}_2{\mathbf{W}} \leq \lceil n/2\rceil$
. Equivalently, it holds that
${\textrm{rank}}_2{\mathbf{W}} \leq \lceil n/2\rceil$
. Equivalently, it holds that
![]() $\textrm{coker}({\mathbf{W}})_2 \cong ({\mathbb{Z}}/2{\mathbb{Z}})^{\ell }$
for some
$\textrm{coker}({\mathbf{W}})_2 \cong ({\mathbb{Z}}/2{\mathbb{Z}})^{\ell }$
for some
![]() $\ell \geq \lfloor n/2\rfloor$
. This is very different behaviour from the distribution for directed graphs in Theorem 1.2 with
$\ell \geq \lfloor n/2\rfloor$
. This is very different behaviour from the distribution for directed graphs in Theorem 1.2 with
![]() $p=2$
since the latter is concentrated on small groups.
$p=2$
since the latter is concentrated on small groups.
For odd primes, numerical evidence suggest that the difference is not as severe. Table 1, namely, suggest that the distribution of
![]() $\textrm{coker}({\mathbf{W}})_{p^m}$
has qualitatively similar behaviour for simple and directed graphs. Quantitatively, however, a close inspection shows that there is a small but nonzero difference that does not seem to disappear when
$\textrm{coker}({\mathbf{W}})_{p^m}$
has qualitatively similar behaviour for simple and directed graphs. Quantitatively, however, a close inspection shows that there is a small but nonzero difference that does not seem to disappear when
![]() $n$
grows large, suggesting that the limiting distribution for simple graphs differs from the one for random directed and weighted graphs. For instance, the estimated probabilities that
$n$
grows large, suggesting that the limiting distribution for simple graphs differs from the one for random directed and weighted graphs. For instance, the estimated probabilities that
![]() $\textrm{coker}({\mathbf{W}})_{p^2}\in \{0,{\mathbb{Z}}/p{\mathbb{Z}} \}$
for
$\textrm{coker}({\mathbf{W}})_{p^2}\in \{0,{\mathbb{Z}}/p{\mathbb{Z}} \}$
for
![]() $p=3$
is
$p=3$
is
![]() $0.758\pm 0.002$
, whereas Theorem 1.2 predicts
$0.758\pm 0.002$
, whereas Theorem 1.2 predicts
![]() $0.747$
.
$0.747$
.
Table 1 Probability that
![]() $\textrm{coker}({\mathbf{W}})_{p^2}\in \{0,{\mathbb{Z}}/p{\mathbb{Z}} \}$
when
$\textrm{coker}({\mathbf{W}})_{p^2}\in \{0,{\mathbb{Z}}/p{\mathbb{Z}} \}$
when
![]() $\mathbf{X}$
is the adjacency matrix of an undirected Erdős–Rényi random graph on
$\mathbf{X}$
is the adjacency matrix of an undirected Erdős–Rényi random graph on
![]() $n$
nodes and
$n$
nodes and
![]() $b = e$
, estimated based on
$b = e$
, estimated based on
![]() $10^5$
independent samples. The estimated values have an uncertainty of
$10^5$
independent samples. The estimated values have an uncertainty of
![]() $\pm 0.002$
. Also displayed is the limiting probability in the case of directed and weighted random graphs, which follows from Theorem 1.2 with
$\pm 0.002$
. Also displayed is the limiting probability in the case of directed and weighted random graphs, which follows from Theorem 1.2 with
![]() $m=2$
. Computation of the group structure of
$m=2$
. Computation of the group structure of
![]() $\textrm{coker}({\mathbf{W}})_{p^2}$
was done using the algorithm smith_form in SageMath [23]
$\textrm{coker}({\mathbf{W}})_{p^2}$
was done using the algorithm smith_form in SageMath [23]

So, the extension of our results to the setting of simple graphs poses an interesting problem, both for odd and even primes. We intend to pursue this in future work. Let us finally recall Conjecture 1.4, and note that a proof of this conjecture would also be valuable since the underlying challenges are also likely to show up in the study of simple graphs. In support of this conjecture, we present numerical data in Table 2, which suggests that the conclusion of Theorem 1.2 remains valid for unweighted directed graphs.
Table 2 Probability that
![]() $\textrm{coker}({\mathbf{W}})_{p^2}\in \{0,{\mathbb{Z}}/p{\mathbb{Z}} \}$
when
$\textrm{coker}({\mathbf{W}})_{p^2}\in \{0,{\mathbb{Z}}/p{\mathbb{Z}} \}$
when
![]() ${\mathbf{X}}\sim \textrm{Unif}\{0,1 \}^{n\times n}$
is the adjacency matrix of an unweighted directed random graph and
${\mathbf{X}}\sim \textrm{Unif}\{0,1 \}^{n\times n}$
is the adjacency matrix of an unweighted directed random graph and
![]() $b = e$
. The same comments as in the caption of Table 1 apply: the estimation used
$b = e$
. The same comments as in the caption of Table 1 apply: the estimation used
![]() $10^5$
independent samples, there is an uncertainty of
$10^5$
independent samples, there is an uncertainty of
![]() $\pm 0.002$
, and SageMath [23] was used
$\pm 0.002$
, and SageMath [23] was used

Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/S0963548324000312.
Acknowledgements
I would like to thank Nils van de Berg, Jaron Sanders, and Haodong Zhu for providing helpful feedback on a draft of this manuscript. I further thank Aida Abiad for an inspiring talk, which motivated my interest in the spectral determinacy of graphs.
This work is part of the project Clustering and Spectral Concentration in Markov Chains with project number OCENW.KLEIN.324 of the research programme Open Competition Domain Science – M, which is partly financed by the Dutch Research Council (NWO).
Competing interests
The author declares none.