Hostname: page-component-55f67697df-zpzq9 Total loading time: 0 Render date: 2025-05-12T17:57:17.775Z Has data issue: false hasContentIssue false
  • English
  • Français

Clustered colouring of graph classes with bounded treedepth or pathwidth

Part of: Graph theory

Published online by Cambridge University Press:  05 July 2022

Sergey Norin ,
Alex Scott  and
David R. Wood
Sergey Norin
Affiliation:
Department of Mathematics and Statistics, McGill University, Montréal, Canada. Supported by NSERC grant 418520
Alex Scott
Affiliation:
Mathematical Institute, University of Oxford, Oxford, UK
David R. Wood*
Affiliation:
School of Mathematics, Monash University, Melbourne, Australia. Supported by the Australian Research Council
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The clustered chromatic number of a class of graphs is the minimum integer 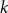$k$ such that for some integer $c$ every graph in the class is 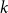$k$ -colourable with monochromatic components of size at most $c$ . We determine the clustered chromatic number of any minor-closed class with bounded treedepth, and prove a best possible upper bound on the clustered chromatic number of any minor-closed class with bounded pathwidth. As a consequence, we determine the fractional clustered chromatic number of every minor-closed class.

Keywords

graphgraph colouringclustered colouringminortreedepthpathwidthfractional colouring

MSC classification

Primary: 05C83: Graph minors
Secondary: 05C15: Coloring of graphs and hypergraphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 32 , Issue 1 , January 2023 , pp. 122 - 133
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alon, N., Ding, G., Oporowski, B. and Vertigan, D. (2003) Partitioning into graphs with only small components. J. Combin. Theory Ser. B 87(2) 231–243.CrossRefGoogle Scholar
Archdeacon, D. (1987) A note on defective colorings of graphs in surfaces. J. Graph Theory 11(4) 517–519.CrossRefGoogle Scholar
Broutin, N. and Kang, R. J. (2018) Bounded monochromatic components for random graphs. J. Comb. 9(3) 411–446.Google Scholar
Choi, I. and Esperet, L. (2019) Improper coloring of graphs on surfaces. J. Graph Theory 91(1) 16–34.CrossRefGoogle Scholar
Cowen, L., Goddard, W. and Jesurum, C. E. (1997) Defective coloring revisited. J. Graph Theory 24(3) 205–219.3.0.CO;2-T>CrossRefGoogle Scholar
Dujmović, V., Esperet, L., Morin, P., Walczak, B. and Wood, D. R. (2022) Clustered 3-colouring graphs of bounded degree. Combin. Probab. Comput. 31(1) 123–135.CrossRefGoogle Scholar
Dvořák, Z. and Norin, S. (2017) Islands in minor-closed classes. I. Bounded treewidth and separators, arXiv: 1710.02727.Google Scholar
Edwards, K., Kang, D. Y., Kim, J., Oum, S. and Seymour, P. (2015) A relative of Hadwiger’s conjecture. SIAM J. Disc. Math. 29(4) 2385–2388.CrossRefGoogle Scholar
Esperet, L. and Joret, G. (2014) Colouring planar graphs with three colours and no large monochromatic components. Combin., Probab. Comput. 23(4) 551–570.CrossRefGoogle Scholar
Haxell, P., Szabó, T. and Tardos, G. (2003) Bounded size components—partitions and transversals. J. Combin. Theory Ser. B 88(2) 281–297.CrossRefGoogle Scholar
Kang, D. Y. and Oum, S. (2019) Improper coloring of graphs with no odd clique minor. Combin. Probab. Comput. 28(5) 740–754.CrossRefGoogle Scholar
Kawarabayashi, K. (2008) A weakening of the odd Hadwiger’s conjecture. Combin. Probab. Comput. 17(6) 815–821.CrossRefGoogle Scholar
Kawarabayashi, K. and Mohar, B. (2007) A relaxed Hadwiger’s conjecture for list colorings. J. Combin. Theory Ser. B 97(4) 647–651.CrossRefGoogle Scholar
Liu, C.-H. and Oum, S. (2018) Partitioning $H$ -minor free graphs into three subgraphs with no large components. J. Combin. Theory Ser. B 128 114–133.CrossRefGoogle Scholar
Liu, C.-H. and Wood, D. R. (2019a) Clustered coloring of graphs excluding a subgraph and a minor , arXiv: 1905.09495.Google Scholar
Liu, C.-H. and Wood, D. R. (2019b) Clustered graph coloring and layered treewidth, arXiv: 1905.08969.Google Scholar
Liu, C.-H. and Wood, D. R. (2022) Clustered variants of Hajós’ conjecture. J. Combin. Theory, Ser. B 152(2) 27–54.CrossRefGoogle Scholar
Mohar, B., Reed, B. and Wood, D. R. (2017) Colourings with bounded monochromatic components in graphs of given circumference. Australas. J. Combin. 69(2) 236–242.Google Scholar
Norin, S., Scott, A., Seymour, P. and Wood, D. R. (2019) Clustered colouring in minor-closed classes. Combinatorica 39(6) 1387–1412.CrossRefGoogle Scholar
Ossona de Mendez, P., Oum, S. and Wood, D. R. (2019) Defective colouring of graphs excluding a subgraph or minor. Combinatorica 39(2) 377–410.CrossRefGoogle Scholar
van den Heuvel, J. and Wood, D. R. (2018) Improper colourings inspired by Hadwiger’s conjecture. J. London Math. Soc. 98(1) 129–148, arXiv: 1704.06536.CrossRefGoogle Scholar
Wood, D. R. (2018) Defective and clustered graph colouring. Electron. J. Combin., DS23, Version 1.CrossRefGoogle Scholar
Nešetřil, J. and Ossona de Mendez, P. (2012) Sparsity, vol. 28. Algorithms and Combinatorics. Springer.CrossRefGoogle Scholar
Eppstein, D. (2020) Pathbreaking for intervals, 11011110. Google Scholar
Dujmović, V., Joret, G., Kozik, J. and Wood, D. R. (2016) Nonrepetitive colouring via entropy compression. Combinatorica 36(6) 661–686.CrossRefGoogle Scholar
Dvořák, Z. and Sereni, J.-S. (2020) On fractional fragility rates of graph classes. Electronic J. Combinat. 27(4) P4.9.CrossRefGoogle Scholar