Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-11T07:26:44.779Z Has data issue: false hasContentIssue false
  • English
  • Français

Clique-factors in graphs with sublinear 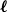$\boldsymbol\ell$-independence number

Part of: Graph theory

Published online by Cambridge University Press:  24 April 2023

Jie Han ,
Ping Hu ,
Guanghui Wang  and
Donglei Yang
Jie Han
Affiliation:
School of Mathematics and Statistics and Center for Applied Mathematics, Beijing Institute of Technology, Beijing, China
Ping Hu
Affiliation:
School of Mathematics, Sun Yat-sen University, Guangzhou, China
Guanghui Wang
Affiliation:
School of Mathematics, Shandong University, Jinan, China
Donglei Yang*
Affiliation:
Data Science Institute, Shandong University, Shandong, China
*
Corresponding author: Donglei Yang; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

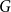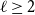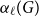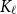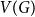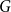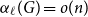Given a graph $G$ and an integer $\ell \ge 2$ , we denote by $\alpha _{\ell }(G)$ the maximum size of a $K_{\ell }$ -free subset of vertices in $V(G)$ . A recent question of Nenadov and Pehova asks for determining the best possible minimum degree conditions forcing clique-factors in $n$ -vertex graphs $G$ with $\alpha _{\ell }(G) = o(n)$ , which can be seen as a Ramsey–Turán variant of the celebrated Hajnal–Szemerédi theorem. 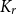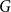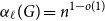In this paper we find the asymptotical sharp minimum degree threshold for $K_r$ -factors in $n$ -vertex graphs $G$ with $\alpha _\ell (G)=n^{1-o(1)}$ for all 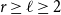$r\ge \ell \ge 2$ .

Keywords

Ramsey–TuránClique-factor

MSC classification

Primary: 05C35: Extremal problems
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 32 , Issue 4 , July 2023 , pp. 665 - 681
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alon, N., Krivelevich, M. and Sudakov, B. (2003) Turán numbers of bipartite graphs and related Ramsey-type questions. Comb. Probab. Comput. 12 477–494. Special issue on Ramsey theory.CrossRefGoogle Scholar
Alon, N. and Yuster, R. (1996) $H$ -factors in dense graphs. J. Comb. Theory Ser. B 66(2) 269–282.CrossRefGoogle Scholar
Balogh, J. and Lenz, J. (2012) Some exact Ramsey–Turán numbers. Bull. Lond. Math. Soc. 44(6) 1251–1258.CrossRefGoogle Scholar
Balogh, J. and Lenz, J. (2013) On Ramsey–Turán numbers of graphs and hypergraphs. Isr. J. Math. 194(1) 45–68.CrossRefGoogle Scholar
Balogh, J., Hu, P. and Simonovits, M. (2015) Phase transitions in Ramsey–Turán theory. J. Comb. Theory Ser. B 114 148–169.CrossRefGoogle Scholar
Balogh, J., Molla, T. and Sharifzadeh, M. (2016) Triangle factors of graphs without large independent sets and of weighted graphs. Random Struct. Algorithms 49(4) 669–693.CrossRefGoogle Scholar
Bollobás, B. and Erdős, P. (1976) On a Ramsey–Turán type problem. J. Comb. Theory Ser. B 21(2) 166–168.CrossRefGoogle Scholar
Chang, F., Han, J., Kim, J., Wang, G. and Yang, D. (2023) Embedding clique-factors in graphs with low $\ell$ -independence number. J. Comb. Theory Ser. B 16 301–330.CrossRefGoogle Scholar
Chang, Y., Han, J., Kohayakawa, Y., Morris, P. and Mota, G. O. (2022) Factors in randomly perturbed hypergraphs. Random Struct. Algorithms 60(2) 153–165.CrossRefGoogle Scholar
Conlon, D., Fox, J. and Sudakov, B. (2009) Ramsey numbers of sparse hypergraphs. Random Struct. Algorithms 35(1) 1–14.CrossRefGoogle Scholar
Diestel, R. (2017) Graph Theory, Vol. 173 of Graduate Texts in Mathematics. Springer.CrossRefGoogle Scholar
Ding, L., Han, J., Sun, S., Wang, G. and Zhou, W. (2022) $F$ -factors in quasi-random hypergraphs. J. Lond. Math. Soc. 106(3) 1810–1843.CrossRefGoogle Scholar
Erdős, P. and Rogers, C. A. (1962) The construction of certain graphs. Can. J. Math. 14 702–707.CrossRefGoogle Scholar
Erdős, P. and Sós, V. T. (1970) Some remarks on Ramsey’s and Turán’s theorem. In Combinatorial theory and its applications, II (Proc. Colloq., Balatonfüred, 1969), pp. 395–404.Google Scholar
Fortuin, C. M., Kasteleyn, P. W. and Ginibre, J. (1971) Correlation inequalities on some partially ordered sets. Commun. Math. Phys. 22(2) 89–103.CrossRefGoogle Scholar
Fox, J., Loh, P.-S. and Zhao, Y. (2015) The critical window for the classical Ramsey-Turán problem. Combinatorica 35(4) 435–476.CrossRefGoogle Scholar
Fox, J. and Sudakov, B. (2011) Dependent random choice. Random Struct. Algorithms 38(1-2) 68–99.CrossRefGoogle Scholar
Hajnal, A. and Szemerédi, E. (1970) Proof of a conjecture of P. Erdős. Comb. Theory Appl. 2(4) 601–623.Google Scholar
Han, J., Morris, P., Wang, G. and Yang, D. (2021) A Ramsey–Turán theory for tilings in graphs. arXiv preprint arXiv:2106.09688 .Google Scholar
Han, J., Zang, C. and Zhao, Y. (2017) Minimum vertex degree thresholds for tiling complete 3-partite 3-graphs. J. Comb. Theory Ser. A 149 115–147.CrossRefGoogle Scholar
Janson, S., Łuczak, T. and Ruciński, A. (1990) An exponential bound for the probability of nonexistence of a specified subgraph in a random graph. In Random Graphs ’87 (Poznań, 1987). Wiley, pp. 73–87.Google Scholar
Keevash, P. and Mycroft, R. (2015) A multipartite Hajnal–Szemerédi theorem. J. Comb. Theory Ser. B 114 187–236.CrossRefGoogle Scholar
Kierstead, H. A. and Kostochka, A. V. (2008) An Ore-type theorem on equitable coloring. J. Comb. Theory Ser. B 98(1) 226–234.CrossRefGoogle Scholar
Kim, J., Kim, Y. and Liu, H. (2019) Two conjectures in Ramsey-Turán theory. SIAM J. Discrete Math. 33(1) 564–586.CrossRefGoogle Scholar
Kim, J. H. (1995) The Ramsey number $R(3,t)$ has order of magnitude $t^2/\log t$ . Random Struct. Algorithms 7(3) 173–207.CrossRefGoogle Scholar
Knierim, C. and Su, P. (2021) $K_r$ -factors in graphs with low independence number. J. Comb. Theory Ser. B 148 60–83.CrossRefGoogle Scholar
Komlós, J. and Simonovits, M. (1996) Szemerédi’s Regularity Lemma and its applications in graph theory. In Combinatorics, Paul Erdős is Eighty, Vol. 2 (Keszthely, 1993). Bolyai Society.Google Scholar
Komlós, J. (2000) Tiling Turán theorems. Combinatorica 20(2) 203–218.Google Scholar
Krivelevich, M. (1997) Triangle factors in random graphs. Comb. Probab. Comput. 6(3) 337–347.CrossRefGoogle Scholar
Kühn, D. and Osthus, D. (2009) The minimum degree threshold for perfect graph packings. Combinatorica 29(1) 65–107.CrossRefGoogle Scholar
Liu, H., Reiher, C., Sharifzadeh, M. and Staden, K. (2021) Geometric constructions for Ramsey–Turán theory. arXiv preprint arXiv:2103.10423 .Google Scholar
Lo, A. and Markström, K. (2015) $F$ -factors in hypergraphs via absorption. Graph Comb. 31(3) 679–712.CrossRefGoogle Scholar
Lüders, C. M. and Reiher, C. (2019) The Ramsey-Turán problem for cliques. Isr. J. Math. 230(2) 613–652.CrossRefGoogle Scholar
Montgomery, R. (2019) Spanning trees in random graphs. Adv. Math. 356 106–793.CrossRefGoogle Scholar
Nenadov, R. and Pehova, Y. (2020) On a Ramsey–Turán variant of the Hajnal–Szemerédi theorem. SIAM J. Discrete Math. 34(2) 1001–1010.CrossRefGoogle Scholar
Rödl, V., Ruciński, A. and Szemerédi, E. (2009) Perfect matchings in large uniform hypergraphs with large minimum collective degree. J. Comb. Theory Ser. A 116(3) 613–636.CrossRefGoogle Scholar
Simonovits, M. and Sós, V. T. (2001) Ramsey–Turán theory. Discrete Math. 229(1-3) 293–340.CrossRefGoogle Scholar
Szemerédi, E. (1972) On graphs containing no complete subgraphs with 4 vertices. Matematikai Lapok. Bolyai János Matematikai Társulat 23 113–116.Google Scholar
Treglown, A. (2015) On directed versions of the Hajnal–Szemerédi theorem. Comb. Probab. Comput. 24(6) 873–928.CrossRefGoogle Scholar