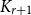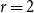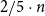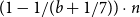1 Introduction
In 1973, Erdős and Simonovits [Reference Erdős and Simonovits8] asked the following question: for each graph H and positive integer k, what
![]() $\delta$
guarantees that every n-vertex H-free graph with minimum degree greater than
$\delta$
guarantees that every n-vertex H-free graph with minimum degree greater than
![]() $\delta n$
is k-colourable? The values of
$\delta n$
is k-colourable? The values of
![]() $\delta$
, as k varies, form the chromatic profile of H-free graphs. More generally, for a family of graphs
$\delta$
, as k varies, form the chromatic profile of H-free graphs. More generally, for a family of graphs
![]() $\mathcal{F}$
, the chromatic profile of
$\mathcal{F}$
, the chromatic profile of
![]() $\mathcal{F}$
is the sequence of values
$\mathcal{F}$
is the sequence of values
![]() $\delta_{\chi}(\mathcal{F}, k)$
where
$\delta_{\chi}(\mathcal{F}, k)$
where
In the case where
![]() $\mathcal{F}$
is the family of H-free graphs, we write
$\mathcal{F}$
is the family of H-free graphs, we write
![]() $\delta_{\chi}(H, k)$
for
$\delta_{\chi}(H, k)$
for
![]() $\delta_{\chi}(\mathcal{F}, k)$
. The question of determining
$\delta_{\chi}(\mathcal{F}, k)$
. The question of determining
![]() $\delta_{\chi}(H, k)$
, first asked in [Reference Erdős and Simonovits8], was re-emphasised by Allen et al. [Reference Allen, Böttcher, Griffiths, Kohayakawa and Morris1]. For general H, very little is known about the chromatic profile and indeed Erdős and Simonovits described it as ‘too complicated’.
$\delta_{\chi}(H, k)$
, first asked in [Reference Erdős and Simonovits8], was re-emphasised by Allen et al. [Reference Allen, Böttcher, Griffiths, Kohayakawa and Morris1]. For general H, very little is known about the chromatic profile and indeed Erdős and Simonovits described it as ‘too complicated’.
There has been much greater success with the chromatic threshold. The chromatic threshold of a family
![]() $\mathcal{F}$
is the limit (and so infimum) of the sequence
$\mathcal{F}$
is the limit (and so infimum) of the sequence
![]() $\delta_{\chi}(\mathcal{F}, k)$
: that is,
$\delta_{\chi}(\mathcal{F}, k)$
: that is,
 \begin{align*}\delta_{\chi}(\mathcal{F}) & = \inf_{k} \delta_{\chi}(\mathcal{F}, k) \\[3pt]& = \inf \{d \colon \exists C = C(\mathcal{F}, d) \text{ such that if } \delta(G) \geqslant d \mathopen{}\left\vert G \right\vert\mathclose{} \text{ and } G \in \mathcal{F}, \text{then } \chi(G) \leqslant C\}.\end{align*}
\begin{align*}\delta_{\chi}(\mathcal{F}) & = \inf_{k} \delta_{\chi}(\mathcal{F}, k) \\[3pt]& = \inf \{d \colon \exists C = C(\mathcal{F}, d) \text{ such that if } \delta(G) \geqslant d \mathopen{}\left\vert G \right\vert\mathclose{} \text{ and } G \in \mathcal{F}, \text{then } \chi(G) \leqslant C\}.\end{align*}
Allen et al. [Reference Allen, Böttcher, Griffiths, Kohayakawa and Morris1] determined the chromatic threshold of H-free graphs for every graph H. They further obtained the chromatic threshold of locally bipartite graphs – the family of graphs in which each neighbourhood is bipartite – confirming the conjecture of Łuczak and Thomassé [Reference Łuczak and Thomassé16] that this threshold is
![]() $1/2$
.
$1/2$
.
Understanding the chromatic profile of locally bipartite graphs is a very natural local to global colouring problem: every neighbourhood is 2-colourable and large, so it seems possible that the whole graph might have small chromatic number. A further motive (that originally brought them to our attention) is to extend the Andrásfai-Erdős-Sós theorem [Reference Andrásfai, Erdős and Sós2] – that theorem gives the first interesting value in the chromatic profile of complete graphs, namely
This theorem can be seen as a minimum degree analogue of Erdős and Simonovits’s stability theorem [Reference Erdős6, Reference Erdős7, Reference Simonovits19] for the structure of
![]() $K_{r + 1}$
-free graphs with close to the maximum number of edges. Erdős and Simonovits’s result says that any H-free graph with
$K_{r + 1}$
-free graphs with close to the maximum number of edges. Erdős and Simonovits’s result says that any H-free graph with
![]() $(1 - 1/r - o(1)) \binom{n}{2}$
edges (where
$(1 - 1/r - o(1)) \binom{n}{2}$
edges (where
![]() $r + 1$
is the chromatic number of H) can be made r-partite by deleting
$r + 1$
is the chromatic number of H) can be made r-partite by deleting
![]() $o(n^{2})$
edges. The natural minimum degree analogue asks what minimum degree guarantees that an H-free graph can be made r-partite by deleting
$o(n^{2})$
edges. The natural minimum degree analogue asks what minimum degree guarantees that an H-free graph can be made r-partite by deleting
![]() $o(n^{2})$
edges. The theorem of Andrásfai, Erdős and Sós answers this for cliques. It turns out that, in order to extend the theorem to non-complete H (as in [Reference Illingworth12]), it is crucial to better understand locally colourable graphs (as defined next), and that is our purpose in this paper.
$o(n^{2})$
edges. The theorem of Andrásfai, Erdős and Sós answers this for cliques. It turns out that, in order to extend the theorem to non-complete H (as in [Reference Illingworth12]), it is crucial to better understand locally colourable graphs (as defined next), and that is our purpose in this paper.
Definition 1.1. A graph is a-locally b-partite if the common neighbourhood of every a-clique is b-colourable. A graph is locally b-partite if it is 1-locally b-partite: the neighbourhood of every vertex is b-colourable. We use
![]() $\mathcal{F}_{a, b}$
to denote the family of a-locally b-partite graphs.
$\mathcal{F}_{a, b}$
to denote the family of a-locally b-partite graphs.
The family of locally bipartite graphs is
![]() $\mathcal{F}_{1, 2}$
. Note that, in general,
$\mathcal{F}_{1, 2}$
. Note that, in general,
In particular,
![]() $\mathcal{F}_{a, b}$
is a subfamily of
$\mathcal{F}_{a, b}$
is a subfamily of
![]() $K_{\ell + 2}$
-free graphs where
$K_{\ell + 2}$
-free graphs where
![]() $\ell = a + b - 1$
.
$\ell = a + b - 1$
.
As mentioned, the Andrásfai-Erdős-Sós theorem gives the first interesting value in the chromatic profile of
![]() $K_{\ell + 2}$
-free graphs, that is, of the family
$K_{\ell + 2}$
-free graphs, that is, of the family
![]() $\mathcal{F}_{\ell, 1}$
. For the basic case of triangle-free graphs, this shows
$\mathcal{F}_{\ell, 1}$
. For the basic case of triangle-free graphs, this shows
![]() $\delta_{\chi}(K_{3}, 2) = 2/5$
. Hajnal (see [Reference Erdős and Simonovits8]) showed that
$\delta_{\chi}(K_{3}, 2) = 2/5$
. Hajnal (see [Reference Erdős and Simonovits8]) showed that
![]() $\delta_{\chi}(K_{3}) \geqslant 1/3$
. Häggkvist [Reference Häggkvist10] showed that
$\delta_{\chi}(K_{3}) \geqslant 1/3$
. Häggkvist [Reference Häggkvist10] showed that
![]() $\delta_{\chi}(K_{3}, 3) \geqslant 10/29$
and Jin [Reference Jin13] proved that equality holds. Finally, building on work of Chen et al. [Reference Chen, Jin and Koh5], Brandt and Thomassé [Reference Brandt and Thomassé4] fully described triangle-free graphs with minimum degree above the chromatic threshold (showing that, in fact,
$\delta_{\chi}(K_{3}, 3) \geqslant 10/29$
and Jin [Reference Jin13] proved that equality holds. Finally, building on work of Chen et al. [Reference Chen, Jin and Koh5], Brandt and Thomassé [Reference Brandt and Thomassé4] fully described triangle-free graphs with minimum degree above the chromatic threshold (showing that, in fact,
![]() $\delta_{\chi}(K_{3}) = \delta_{\chi}(K_{3}, 4) = 1/3$
). Moreover, Goddard and Lyle [Reference Goddard and Lyle9], and Nikiforov [Reference Nikiforov17] independently showed that the chromatic profile of
$\delta_{\chi}(K_{3}) = \delta_{\chi}(K_{3}, 4) = 1/3$
). Moreover, Goddard and Lyle [Reference Goddard and Lyle9], and Nikiforov [Reference Nikiforov17] independently showed that the chromatic profile of
![]() $K_{r + 2}$
-free graphs can be derived straightforwardly from that of triangle-free graphs. The chromatic profile of the
$K_{r + 2}$
-free graphs can be derived straightforwardly from that of triangle-free graphs. The chromatic profile of the
![]() $K_{\ell + 2}$
-free graphs, that is, of
$K_{\ell + 2}$
-free graphs, that is, of
![]() $\mathcal{F}_{\ell, 1}$
, has thus been completely determined.
$\mathcal{F}_{\ell, 1}$
, has thus been completely determined.
The chromatic profile of the family
![]() $\mathcal{F}_{a, b}$
for
$\mathcal{F}_{a, b}$
for
![]() $b \geqslant 2$
displays substantially different behaviour to the case
$b \geqslant 2$
displays substantially different behaviour to the case
![]() $b = 1$
, however. In Section 2, we determine the chromatic threshold of the family of a-locally b-partite graphs. This result in the special case
$b = 1$
, however. In Section 2, we determine the chromatic threshold of the family of a-locally b-partite graphs. This result in the special case
![]() $a = 1$
and
$a = 1$
and
![]() $b = 2$
was conjectured (with a construction for the lower bound) by Łuczak and Thomassé [Reference Łuczak and Thomassé16] and proved by Allen et al. [Reference Allen, Böttcher, Griffiths, Kohayakawa and Morris1].
$b = 2$
was conjectured (with a construction for the lower bound) by Łuczak and Thomassé [Reference Łuczak and Thomassé16] and proved by Allen et al. [Reference Allen, Böttcher, Griffiths, Kohayakawa and Morris1].
Theorem 1.2. Let a and b be positive integers with
![]() $b \geqslant 2$
and let
$b \geqslant 2$
and let
![]() $\ell = a + b - 1$
. Then,
$\ell = a + b - 1$
. Then,
and, in particular, the chromatic threshold of locally b-partite graphs,
![]() $\delta_{\chi}(\mathcal{F}_{1, b})$
, is
$\delta_{\chi}(\mathcal{F}_{1, b})$
, is
![]() $1 - 1/b$
.
$1 - 1/b$
.
For comparison, the chromatic threshold of the family
![]() $\mathcal{F}_{\ell, 1}$
of
$\mathcal{F}_{\ell, 1}$
of
![]() $K_{\ell + 2}$
-free graphs is
$K_{\ell + 2}$
-free graphs is
![]() $1 - 1/(\ell + 1/2)$
.
$1 - 1/(\ell + 1/2)$
.
Now for the chromatic profile. All a-locally b-partite graphs are
![]() $K_{a + b + 1}$
-free, and furthermore, the n-vertex
$K_{a + b + 1}$
-free, and furthermore, the n-vertex
![]() $K_{a + b + 1}$
-free graph with highest minimum degree (and most edges), the Turán graph [Reference Turán20],
$K_{a + b + 1}$
-free graph with highest minimum degree (and most edges), the Turán graph [Reference Turán20],
![]() $T_{a + b}(n)$
is a-locally b-partite and
$T_{a + b}(n)$
is a-locally b-partite and
![]() $(a + b)$
-chromatic. In particular,
$(a + b)$
-chromatic. In particular,
since there are no
![]() $K_{a + b + 1}$
-free graphs (and so no a-locally b-partite) with
$K_{a + b + 1}$
-free graphs (and so no a-locally b-partite) with
![]() $\delta(G) > (1 - 1/(a + b)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. In particular, the first interesting value in the chromatic profile of a-locally b-partite graphs is
$\delta(G) > (1 - 1/(a + b)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. In particular, the first interesting value in the chromatic profile of a-locally b-partite graphs is
![]() $\delta_{\chi}(\mathcal{F}_{a, b}, \ell + 1)$
. An upper bound for this is given by Theorems 1.3 (
$\delta_{\chi}(\mathcal{F}_{a, b}, \ell + 1)$
. An upper bound for this is given by Theorems 1.3 (
![]() $b \geqslant 3$
) and 1.4 (
$b \geqslant 3$
) and 1.4 (
![]() $b = 2$
). In Section 4, we prove Theorem 1.3 for locally b-partite graphs (that is, for
$b = 2$
). In Section 4, we prove Theorem 1.3 for locally b-partite graphs (that is, for
![]() $a = 1$
), and in Section 5, we extend it to all a and prove Theorem 1.4.
$a = 1$
), and in Section 5, we extend it to all a and prove Theorem 1.4.
Theorem 1.3. Let a and b be positive integers with
![]() $b \geqslant 3$
and let
$b \geqslant 3$
and let
![]() $\ell = a + b - 1$
. Then,
$\ell = a + b - 1$
. Then,
and, in particular, every locally b-partite graph G with
![]() $\delta(G) > (1 - 1/(b + 1/7)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
is
$\delta(G) > (1 - 1/(b + 1/7)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
is
![]() $(b + 1)$
-colourable.
$(b + 1)$
-colourable.
Theorem 1.4. Let a be a positive integer and
![]() $\ell = a + 1$
. Then,
$\ell = a + 1$
. Then,
Note that the chromatic threshold of the family of
![]() $K_{\ell + 2}$
-free graphs is
$K_{\ell + 2}$
-free graphs is
![]() $1 - 1/(\ell + 1/2)$
. In particular, all chromatic profile values for
$1 - 1/(\ell + 1/2)$
. In particular, all chromatic profile values for
![]() $K_{\ell + 2}$
-free graphs are greater than the first interesting value for a-locally b-partite ones (
$K_{\ell + 2}$
-free graphs are greater than the first interesting value for a-locally b-partite ones (
![]() $b \geqslant 2$
).
$b \geqslant 2$
).
To extend the chromatic profile of triangle-free graphs to
![]() $K_{r + 1}$
-free graphs as mentioned above, Goddard and Lyle [Reference Goddard and Lyle9], and Nikiforov [Reference Nikiforov17] showed that every n-vertex maximal
$K_{r + 1}$
-free graphs as mentioned above, Goddard and Lyle [Reference Goddard and Lyle9], and Nikiforov [Reference Nikiforov17] showed that every n-vertex maximal
![]() $K_{r + 1}$
-free graph with minimum degree greater than
$K_{r + 1}$
-free graph with minimum degree greater than
![]() $\delta_{\chi}(K_{r + 1}) \cdot n$
consists of an independent set joined to a
$\delta_{\chi}(K_{r + 1}) \cdot n$
consists of an independent set joined to a
![]() $K_{r}$
-free graph. That is, maximal graphs of
$K_{r}$
-free graph. That is, maximal graphs of
![]() $\mathcal{F}_{r, 1}$
with sufficiently large minimum degree are obtained from those in
$\mathcal{F}_{r, 1}$
with sufficiently large minimum degree are obtained from those in
![]() $\mathcal{F}_{r - 1, 1}$
by joining an independent set. A simple induction then converts the structure of triangle-free graphs to the structure of
$\mathcal{F}_{r - 1, 1}$
by joining an independent set. A simple induction then converts the structure of triangle-free graphs to the structure of
![]() $K_{r + 1}$
-free graphs. It is natural to ask whether something similar can be done to convert between different families
$K_{r + 1}$
-free graphs. It is natural to ask whether something similar can be done to convert between different families
![]() $\mathcal{F}_{a, b}$
. Firstly, there does not seem to be an easy way to convert between
$\mathcal{F}_{a, b}$
. Firstly, there does not seem to be an easy way to convert between
![]() $\mathcal{F}_{a, b - 1}$
and
$\mathcal{F}_{a, b - 1}$
and
![]() $\mathcal{F}_{a, b}$
(certainly joining on an independent set fails). Although we obtain the upper bound for
$\mathcal{F}_{a, b}$
(certainly joining on an independent set fails). Although we obtain the upper bound for
![]() $\delta_{\chi}(\mathcal{F}_{1, b}, b + 1)$
in Theorem 1.3 using knowledge of locally bipartite graphs, it is not a straightforward induction.
$\delta_{\chi}(\mathcal{F}_{1, b}, b + 1)$
in Theorem 1.3 using knowledge of locally bipartite graphs, it is not a straightforward induction.
Joining on an independent set to a graph in
![]() $\mathcal{F}_{a - 1, b}$
does give a graph in
$\mathcal{F}_{a - 1, b}$
does give a graph in
![]() $\mathcal{F}_{a, b}$
, but it is not clear that all maximal graphs in
$\mathcal{F}_{a, b}$
, but it is not clear that all maximal graphs in
![]() $\mathcal{F}_{a, b}$
of large minimum degree are obtained in this way – the lower value of
$\mathcal{F}_{a, b}$
of large minimum degree are obtained in this way – the lower value of
![]() $\delta_{\chi}(\mathcal{F}_{a, b})$
for
$\delta_{\chi}(\mathcal{F}_{a, b})$
for
![]() $b \geqslant 2$
means the structural lemma of Goddard, Lyle and Nikiforov does not apply. While our arguments extending results from locally b-partite graphs to a-locally b-partite graphs are simpler, they interestingly do require knowledge of locally b
$b \geqslant 2$
means the structural lemma of Goddard, Lyle and Nikiforov does not apply. While our arguments extending results from locally b-partite graphs to a-locally b-partite graphs are simpler, they interestingly do require knowledge of locally b
![]() $^{\prime}$
-partite graphs for all
$^{\prime}$
-partite graphs for all
![]() $b' \leqslant a + b$
. It seems that the crux of understanding locally colourable graphs is understanding locally b-partite graphs, a sentiment we will crystallise in Section 5.
$b' \leqslant a + b$
. It seems that the crux of understanding locally colourable graphs is understanding locally b-partite graphs, a sentiment we will crystallise in Section 5.
Some of the required knowledge of locally bipartite graphs was obtained by the author in [Reference Illingworth11], which included results such as
The results in [Reference Illingworth11] give detailed information about n-vertex locally bipartite graphs with minimum degree greater than
![]() $6/11 \cdot n$
, including homomorphism properties. However, in order to prove the upper bound for
$6/11 \cdot n$
, including homomorphism properties. However, in order to prove the upper bound for
![]() $\delta_{\chi}(\mathcal{F}_{1, b}, b + 1)$
in Theorem 1.3, we need to extend our structural knowledge of locally bipartite graphs down to
$\delta_{\chi}(\mathcal{F}_{1, b}, b + 1)$
in Theorem 1.3, we need to extend our structural knowledge of locally bipartite graphs down to
![]() $8/15$
, though, fortunately, we do not need any homomorphism properties. We do this in Section 3 and our full knowledge of locally bipartite graphs is summarised there in Theorem 3.1.
$8/15$
, though, fortunately, we do not need any homomorphism properties. We do this in Section 3 and our full knowledge of locally bipartite graphs is summarised there in Theorem 3.1.
1.1 Notation
Let G be a graph and
![]() $X \subset V(G)$
. We write
$X \subset V(G)$
. We write
![]() $\Gamma(X)$
for
$\Gamma(X)$
for
![]() $\cap_{v \in X} \Gamma(v)$
(the common neighbourhood of the vertices of X) and d(X) for
$\cap_{v \in X} \Gamma(v)$
(the common neighbourhood of the vertices of X) and d(X) for
![]() $\mathopen{}\left\vert \Gamma(X) \right\vert\mathclose{}$
. We often omit the parentheses so
$\mathopen{}\left\vert \Gamma(X) \right\vert\mathclose{}$
. We often omit the parentheses so
![]() $\Gamma(u, v) = \Gamma(u) \cap \Gamma(v)$
and
$\Gamma(u, v) = \Gamma(u) \cap \Gamma(v)$
and
![]() $d(u, v) = \mathopen{}\left\vert \Gamma(u, v) \right\vert\mathclose{}$
. We write
$d(u, v) = \mathopen{}\left\vert \Gamma(u, v) \right\vert\mathclose{}$
. We write
![]() $G_{X}$
for
$G_{X}$
for
![]() $G[\Gamma(X)]$
so, for example,
$G[\Gamma(X)]$
so, for example,
![]() $G_{u, v}$
is the induced graph on the common neighbourhood of vertices u and v. Note that G being a-locally b-partite is equivalent to
$G_{u, v}$
is the induced graph on the common neighbourhood of vertices u and v. Note that G being a-locally b-partite is equivalent to
![]() $\chi(G_{K}) \leqslant b$
for every a-clique K of G. We make frequent use of the fact that for two vertices u and v of G
$\chi(G_{K}) \leqslant b$
for every a-clique K of G. We make frequent use of the fact that for two vertices u and v of G
Given a set of vertices
![]() $X \subset V(G)$
, we write e(X, G) for the number of ordered pairs of vertices (x, v) with
$X \subset V(G)$
, we write e(X, G) for the number of ordered pairs of vertices (x, v) with
![]() $x \in X$
,
$x \in X$
,
![]() $v \in G$
and xv an edge in G. In particular, e(X, G) counts each edge in G[X] twice and each edge from X to
$v \in G$
and xv an edge in G. In particular, e(X, G) counts each edge in G[X] twice and each edge from X to
![]() $G - X$
once and satisfies
$G - X$
once and satisfies
We generalise this notation to vertex weightings which will appear in many of our arguments. We will take a set of vertices
![]() $X \subset V(G)$
and assign weights
$X \subset V(G)$
and assign weights
![]() $\omega \colon X \rightarrow \mathbb{Z}_{\geqslant 0}$
to the vertices of X. Then, we define
$\omega \colon X \rightarrow \mathbb{Z}_{\geqslant 0}$
to the vertices of X. Then, we define
We will often use the word circuit (as opposed to cycle) in our arguments. A circuit is a sequence of (not necessarily distinct) vertices
![]() $v_{1}, v_{2}, \dotsc, v_{\ell}$
with
$v_{1}, v_{2}, \dotsc, v_{\ell}$
with
![]() $\ell > 1$
,
$\ell > 1$
,
![]() $v_{i}$
adjacent to
$v_{i}$
adjacent to
![]() $v_{i + 1}$
(for
$v_{i + 1}$
(for
![]() $i = 1, 2, \dotsc,$
$i = 1, 2, \dotsc,$
![]() $\ell - 1$
) and
$\ell - 1$
) and
![]() $v_{\ell}$
adjacent to
$v_{\ell}$
adjacent to
![]() $v_{1}$
. Note that in a locally bipartite graph, the neighbourhood of any vertex does not contain an odd circuit (and of course does not contain an odd cycle). We use circuit to avoid considering whether some pairs of vertices are distinct when it is unnecessary to do so.
$v_{1}$
. Note that in a locally bipartite graph, the neighbourhood of any vertex does not contain an odd circuit (and of course does not contain an odd cycle). We use circuit to avoid considering whether some pairs of vertices are distinct when it is unnecessary to do so.
Given a graph G, a blow-up of G is a graph obtained by replacing each vertex v of G by a non-empty independent set
![]() $I_{v}$
and each edge uv by a complete bipartite graph between classes
$I_{v}$
and each edge uv by a complete bipartite graph between classes
![]() $I_{u}$
and
$I_{u}$
and
![]() $I_{v}$
. We say we have blown-up a vertex v by n if
$I_{v}$
. We say we have blown-up a vertex v by n if
![]() $\mathopen{}\left\vert I_{v} \right\vert\mathclose{} = n$
. It is often helpful to think of this as weighting vertex v by n.
$\mathopen{}\left\vert I_{v} \right\vert\mathclose{} = n$
. It is often helpful to think of this as weighting vertex v by n.
A blow-up is balanced if the independent sets
![]() $(I_{v})_{v \in G}$
are as equal in size as possible. We use G(t) to denote the graph obtained by blowing-up each vertex of G by t: G(t) is the balanced blow-up of G on
$(I_{v})_{v \in G}$
are as equal in size as possible. We use G(t) to denote the graph obtained by blowing-up each vertex of G by t: G(t) is the balanced blow-up of G on
![]() $t \mathopen{}\left\vert G \right\vert\mathclose{}$
vertices. Note, for example, that the balanced blow-ups of the clique,
$t \mathopen{}\left\vert G \right\vert\mathclose{}$
vertices. Note, for example, that the balanced blow-ups of the clique,
![]() $K_{r}$
, are exactly the Turán graphs,
$K_{r}$
, are exactly the Turán graphs,
![]() $T_{r}(n)$
. We note in passing that a graph has the same chromatic and clique number as any of its blow-ups. Furthermore, if H is a blow-up of G, then G is a-locally b-partite if and only if H is a-locally b-partite.
$T_{r}(n)$
. We note in passing that a graph has the same chromatic and clique number as any of its blow-ups. Furthermore, if H is a blow-up of G, then G is a-locally b-partite if and only if H is a-locally b-partite.
Given two graphs G and H, the join of G and H, denoted
![]() $G + H$
, is the graph obtained by taking disjoint copies of G and H and joining each vertex of the copy of G to each vertex of the copy of H. Note that the chromatic and clique numbers of
$G + H$
, is the graph obtained by taking disjoint copies of G and H and joining each vertex of the copy of G to each vertex of the copy of H. Note that the chromatic and clique numbers of
![]() $G + H$
are the sum of the chromatic and clique numbers of G and H.
$G + H$
are the sum of the chromatic and clique numbers of G and H.
A graph G is homomorphic to a graph H, written
![]() $G \rightarrow H$
, if there is a map
$G \rightarrow H$
, if there is a map
![]() $\varphi \colon V(G) \rightarrow V(H)$
such that for any edge uv of G,
$\varphi \colon V(G) \rightarrow V(H)$
such that for any edge uv of G,
![]() $\varphi(u)\varphi(v)$
is an edge of H. A graph G is homomorphic to a graph H if and only if G is a subgraph of some blow-up of H. In particular, if
$\varphi(u)\varphi(v)$
is an edge of H. A graph G is homomorphic to a graph H if and only if G is a subgraph of some blow-up of H. In particular, if
![]() $G \rightarrow H$
, then
$G \rightarrow H$
, then
![]() $\chi(G) \leqslant \chi(H)$
and, moreover, if H is a-locally b-partite, then G is also.
$\chi(G) \leqslant \chi(H)$
and, moreover, if H is a-locally b-partite, then G is also.
1.2 Importance to extending the Andrásfai-Erdős-Sós theorem
As previously mentioned, our initial motivation for studying locally colourable graphs came from trying to extend the Andrásfai-Erdős-Sós theorem [Reference Andrásfai, Erdős and Sós2] to non-complete graphs and obtain a minimum degree analogue of Erdős and Simonovits’s classical stability theorem [Reference Erdős6, Reference Erdős7, Reference Simonovits19]. In particular, we wish to determine, for each
![]() $(r + 1)$
-chromatic H, the value of
$(r + 1)$
-chromatic H, the value of
Here we sketch the link between this and locally colourable graphs deferring a thorough treatment to [Reference Illingworth12]. When
![]() $r = 2$
the situation is particularly clean.
$r = 2$
the situation is particularly clean.
Theorem 1.5. Let H be a 3-chromatic graph. There is a smallest positive integer g such that H is not homomorphic to
![]() $C_{2g + 1}$
. Then
$C_{2g + 1}$
. Then
The graph that shows
![]() $\delta_{H} \geqslant 2/(2g + 1)$
is a balanced blow-up of the cycle
$\delta_{H} \geqslant 2/(2g + 1)$
is a balanced blow-up of the cycle
![]() $C_{2g + 1}$
. The intuitive explanation for the theorem is that the main obstacle for being close to (that is, within
$C_{2g + 1}$
. The intuitive explanation for the theorem is that the main obstacle for being close to (that is, within
![]() $o(n^{2})$
edges of) bipartite is containing some blow-up of an odd cycle. That odd cycle must be consistent with being H-free (in particular, the blow-up of the odd cycle must be H-free), and hence, it is the first odd cycle to which H is not homomorphic that determines
$o(n^{2})$
edges of) bipartite is containing some blow-up of an odd cycle. That odd cycle must be consistent with being H-free (in particular, the blow-up of the odd cycle must be H-free), and hence, it is the first odd cycle to which H is not homomorphic that determines
![]() $\delta_{H}$
.
$\delta_{H}$
.
Understanding locally colourable graphs becomes crucial when extending this theorem to
![]() $r \geqslant 3$
. For concreteness, consider
$r \geqslant 3$
. For concreteness, consider
![]() $r = 3$
: we are interested in which graphs’ blow-ups are the main obstacles for being close to tripartite. Given the importance of odd cycles when
$r = 3$
: we are interested in which graphs’ blow-ups are the main obstacles for being close to tripartite. Given the importance of odd cycles when
![]() $r = 2,$
it seems natural that odd wheels (the join of a single vertex and an odd cycle) would be obstacles here and indeed they are. However, there are further obstacles that do not contain odd wheels and so are locally bipartite. These observations suggest we should pay attention to 4-chromatic locally bipartite graphs as these may be obstacles for being close to tripartite. Many of the graphs appearing in our theorems here also play a leading role for minimum degree stability.
$r = 2,$
it seems natural that odd wheels (the join of a single vertex and an odd cycle) would be obstacles here and indeed they are. However, there are further obstacles that do not contain odd wheels and so are locally bipartite. These observations suggest we should pay attention to 4-chromatic locally bipartite graphs as these may be obstacles for being close to tripartite. Many of the graphs appearing in our theorems here also play a leading role for minimum degree stability.
2 Chromatic thresholds
The
![]() $(r - 1)$
-locally 1-partite graphs are exactly the
$(r - 1)$
-locally 1-partite graphs are exactly the
![]() $K_{r + 1}$
-free graphs, and their chromatic threshold was determined by Goddard and Lyle [Reference Goddard and Lyle9], and Nikiforov [Reference Nikiforov17].
$K_{r + 1}$
-free graphs, and their chromatic threshold was determined by Goddard and Lyle [Reference Goddard and Lyle9], and Nikiforov [Reference Nikiforov17].
In this section, we prove Theorem 1.2, showing that
![]() $\delta_{\chi}(\mathcal{F}_{a, b}) = 1 - 1/(a + b - 1)$
for all
$\delta_{\chi}(\mathcal{F}_{a, b}) = 1 - 1/(a + b - 1)$
for all
![]() $a \geqslant 1$
and
$a \geqslant 1$
and
![]() $b \geqslant 2$
. The upper bound follows from the work of Allen et al. [Reference Allen, Böttcher, Griffiths, Kohayakawa and Morris1].
$b \geqslant 2$
. The upper bound follows from the work of Allen et al. [Reference Allen, Böttcher, Griffiths, Kohayakawa and Morris1].
Proof of upper bound in Theorem 1.2. Fix a and b positive integers with
![]() $b \geqslant 2$
and let
$b \geqslant 2$
and let
![]() $\ell = a + b - 1$
. Let
$\ell = a + b - 1$
. Let
![]() $d > 1 - 1/\ell$
and let
$d > 1 - 1/\ell$
and let
![]() $G \in \mathcal{F}_{a, b}$
with
$G \in \mathcal{F}_{a, b}$
with
![]() $\delta(G) \geqslant d \mathopen{}\left\vert G \right\vert\mathclose{}$
. Now
$\delta(G) \geqslant d \mathopen{}\left\vert G \right\vert\mathclose{}$
. Now
![]() $K_{\ell - 1} + C_{5}$
has an a-clique whose common neighbourhoods contains
$K_{\ell - 1} + C_{5}$
has an a-clique whose common neighbourhoods contains
![]() $K_{b - 2} + C_{5}$
so is not b-colourable. In particular, G is
$K_{b - 2} + C_{5}$
so is not b-colourable. In particular, G is
![]() $(K_{\ell - 1} + C_{5})$
-free.
$(K_{\ell - 1} + C_{5})$
-free.
Now, in the language of [Reference Allen, Böttcher, Griffiths, Kohayakawa and Morris1],
![]() $K_{\ell - 1} + C_{5}$
is
$K_{\ell - 1} + C_{5}$
is
![]() $(\ell + 2)$
-near-acyclic, so the chromatic threshold of the family of
$(\ell + 2)$
-near-acyclic, so the chromatic threshold of the family of
![]() $(K_{\ell - 1} + C_{5})$
-free graphs is
$(K_{\ell - 1} + C_{5})$
-free graphs is
![]() $1 - 1/\ell$
. In particular, there is a constant C depending only upon d and
$1 - 1/\ell$
. In particular, there is a constant C depending only upon d and
![]() $\ell$
(and not on G) such that
$\ell$
(and not on G) such that
![]() $\chi(G) \leqslant C$
. Hence,
$\chi(G) \leqslant C$
. Hence,
For the lower bound, it suffices to give examples of graphs
![]() $G \in \mathcal{F}_{a, b}$
with
$G \in \mathcal{F}_{a, b}$
with
![]() $\delta(G) \geqslant (1 - 1/(a + b - 1) - o(1)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
which have arbitrarily large chromatic number. Allen et al. [Reference Allen, Böttcher, Griffiths, Kohayakawa and Morris1] used graphs of large girth and high chromatic number as well as Borsuk-Hajnal graphs for their lower bounds. However, these depend upon the forbidden subgraph H and do not seem to be applicable here where the collection of forbidden subgraphs is infinite. Łuczak and Thomassé [Reference Łuczak and Thomassé16] modified a Borsuk graph to give the lower bound of 1/2 for the chromatic threshold of locally bipartite graphs. We will give a somewhat simpler example which gives the lower bound for all
$\delta(G) \geqslant (1 - 1/(a + b - 1) - o(1)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
which have arbitrarily large chromatic number. Allen et al. [Reference Allen, Böttcher, Griffiths, Kohayakawa and Morris1] used graphs of large girth and high chromatic number as well as Borsuk-Hajnal graphs for their lower bounds. However, these depend upon the forbidden subgraph H and do not seem to be applicable here where the collection of forbidden subgraphs is infinite. Łuczak and Thomassé [Reference Łuczak and Thomassé16] modified a Borsuk graph to give the lower bound of 1/2 for the chromatic threshold of locally bipartite graphs. We will give a somewhat simpler example which gives the lower bound for all
![]() $\mathcal{F}_{a, b}$
(
$\mathcal{F}_{a, b}$
(
![]() $a \geqslant 1, b \geqslant 2$
).
$a \geqslant 1, b \geqslant 2$
).
Our example is based upon the classical Schrijver graph [18]. The Kneser graph,
![]() $\operatorname{KG}(n, k)$
, is the graph whose vertex set is all k-subsets of
$\operatorname{KG}(n, k)$
, is the graph whose vertex set is all k-subsets of
![]() $\mathopen{}\left\{1, 2, \dotsc, n\right\}\mathclose{}$
with two vertices adjacent if the corresponding k-sets are disjoint. In 1955, Kneser [Reference Kneser14] conjectured that the chromatic number of
$\mathopen{}\left\{1, 2, \dotsc, n\right\}\mathclose{}$
with two vertices adjacent if the corresponding k-sets are disjoint. In 1955, Kneser [Reference Kneser14] conjectured that the chromatic number of
![]() $\operatorname{KG}(n, k)$
is
$\operatorname{KG}(n, k)$
is
![]() $n - 2k + 2$
. This conjecture remained open for two decades and was first proved by Lovász [Reference Lovász15] using homotopy theory (see also Bárány [Reference Bárány3] for a very short proof).
$n - 2k + 2$
. This conjecture remained open for two decades and was first proved by Lovász [Reference Lovász15] using homotopy theory (see also Bárány [Reference Bárány3] for a very short proof).
The Schrijver graph,
![]() $\operatorname{SG}(n, k)$
, is the graph whose vertex set is all k-subsets of
$\operatorname{SG}(n, k)$
, is the graph whose vertex set is all k-subsets of
![]() $\mathopen{}\left\{1, 2, \dotsc, n\right\}\mathclose{}$
which do not contain both i and
$\mathopen{}\left\{1, 2, \dotsc, n\right\}\mathclose{}$
which do not contain both i and
![]() $i + 1$
for any
$i + 1$
for any
![]() $i = 1, 2, \dotsc, n - 1$
and do not contain both n and 1. Again, vertices are adjacent if the corresponding k-sets are disjoint. Put another way,
$i = 1, 2, \dotsc, n - 1$
and do not contain both n and 1. Again, vertices are adjacent if the corresponding k-sets are disjoint. Put another way,
![]() $\operatorname{SG}(n, k)$
is the induced subgraph of
$\operatorname{SG}(n, k)$
is the induced subgraph of
![]() $\operatorname{KG}(n, k)$
obtained by deleting all vertices whose corresponding sets are supersets of any of
$\operatorname{KG}(n, k)$
obtained by deleting all vertices whose corresponding sets are supersets of any of
![]() $\mathopen{}\left\{1, 2\right\}\mathclose{}$
,
$\mathopen{}\left\{1, 2\right\}\mathclose{}$
,
![]() $\mathopen{}\left\{2, 3\right\}\mathclose{}$
,
$\mathopen{}\left\{2, 3\right\}\mathclose{}$
,
![]() $\mathopen{}\left\{3, 4\right\}\mathclose{}$
, …,
$\mathopen{}\left\{3, 4\right\}\mathclose{}$
, …,
![]() $\mathopen{}\left\{n - 1, n\right\}\mathclose{}$
,
$\mathopen{}\left\{n - 1, n\right\}\mathclose{}$
,
![]() $\mathopen{}\left\{n, 1\right\}\mathclose{}$
. Schrijver [18] showed that
$\mathopen{}\left\{n, 1\right\}\mathclose{}$
. Schrijver [18] showed that
![]() $\operatorname{SG}(n, k)$
is vertex-critical with chromatic number
$\operatorname{SG}(n, k)$
is vertex-critical with chromatic number
![]() $\chi(\operatorname{SG}(n, k)) = \chi(\operatorname{KG}(n, k)) = n - 2k + 2$
.
$\chi(\operatorname{SG}(n, k)) = \chi(\operatorname{KG}(n, k)) = n - 2k + 2$
.
Proof of lower bound in Theorem 1.2. Fix a and b positive integers with
![]() $b \geqslant 2$
and let
$b \geqslant 2$
and let
![]() $\ell = a + b - 1$
. Fix k and let
$\ell = a + b - 1$
. Fix k and let
![]() $n = 2k + f(k)$
where f(k) is a non-negative integer less than k, and both
$n = 2k + f(k)$
where f(k) is a non-negative integer less than k, and both
![]() $f(k) \rightarrow \infty$
,
$f(k) \rightarrow \infty$
,
![]() $f(k)/k \rightarrow 0$
as
$f(k)/k \rightarrow 0$
as
![]() $k \rightarrow \infty$
. Since
$k \rightarrow \infty$
. Since
![]() $k > n/3$
, the graph
$k > n/3$
, the graph
![]() $\operatorname{SG}(n, k)$
is triangle-free. We will eventually consider a blow-up of the graph shown in Figure 1.
$\operatorname{SG}(n, k)$
is triangle-free. We will eventually consider a blow-up of the graph shown in Figure 1.
-
Each rectangle is an independent set of n vertices:
 $v_{1, 2}$
,
$v_{1, 2}$
,
 $v_{2, 3}$
, …,
$v_{2, 3}$
, …,
 $v_{n - 1, n}$
,
$v_{n - 1, n}$
,
 $v_{n, 1}$
– we always consider indices modulo n.
$v_{n, 1}$
– we always consider indices modulo n. -
There are
 $\ell - 1$
rectangles and the vertices in rectangles form a complete
$\ell - 1$
rectangles and the vertices in rectangles form a complete
 $(\ell - 1)$
-partite graph with n vertices in each part.
$(\ell - 1)$
-partite graph with n vertices in each part. -
The vertex v is adjacent to all of the
 $v_{i, i + 1}$
but has no neighbours in the copy of
$v_{i, i + 1}$
but has no neighbours in the copy of
 $\operatorname{SG}(n, k)$
– in particular, the rectangles together with v form a complete
$\operatorname{SG}(n, k)$
– in particular, the rectangles together with v form a complete
 $\ell$
-partite graph.
$\ell$
-partite graph. -
Finally,
 $A \in \operatorname{SG}(n, k)$
is adjacent to
$A \in \operatorname{SG}(n, k)$
is adjacent to
 $v_{i, i + 1}$
if either i or
$v_{i, i + 1}$
if either i or
 $i + 1$
is in A (note, by the definition of the Schrijver graph, that it is impossible for both i and
$i + 1$
is in A (note, by the definition of the Schrijver graph, that it is impossible for both i and
 $i + 1$
to be in A).
$i + 1$
to be in A).
We first check that the graph, G, shown in Figure 1 is locally
![]() $\ell$
-partite. Fix a vertex u of G. If
$\ell$
-partite. Fix a vertex u of G. If
![]() $u = v$
, then
$u = v$
, then
![]() $G_{u}$
consists of the
$G_{u}$
consists of the
![]() $\ell - 1$
rectangles and so is
$\ell - 1$
rectangles and so is
![]() $(\ell - 1)$
-colourable. Next suppose that u is a vertex in the copy of
$(\ell - 1)$
-colourable. Next suppose that u is a vertex in the copy of
![]() $\operatorname{SG}(n, k)$
, so
$\operatorname{SG}(n, k)$
, so
![]() $v \not \in \Gamma(u)$
. As
$v \not \in \Gamma(u)$
. As
![]() $\operatorname{SG}(n, k)$
is triangle-free,
$\operatorname{SG}(n, k)$
is triangle-free,
![]() $\Gamma(u)$
consists of an independent set in
$\Gamma(u)$
consists of an independent set in
![]() $\operatorname{SG}(n, k)$
together with some vertices from the
$\operatorname{SG}(n, k)$
together with some vertices from the
![]() $\ell - 1$
rectangles. In particular,
$\ell - 1$
rectangles. In particular,
![]() $G_{u}$
is
$G_{u}$
is
![]() $\ell$
-colourable. Finally, suppose that u lies in the
$\ell$
-colourable. Finally, suppose that u lies in the
![]() $\ell - 1$
rectangles. By symmetry, we may take u to be a
$\ell - 1$
rectangles. By symmetry, we may take u to be a
![]() $v_{1, 2}$
. Then,
$v_{1, 2}$
. Then,
![]() $\Gamma(u)$
consists of two independent sets in
$\Gamma(u)$
consists of two independent sets in
![]() $\operatorname{SG}(n, k)$
(sets containing 1 and sets containing 2),
$\operatorname{SG}(n, k)$
(sets containing 1 and sets containing 2),
![]() $\ell - 2$
rectangles and v. There are no edges from v to the copy of
$\ell - 2$
rectangles and v. There are no edges from v to the copy of
![]() $\operatorname{SG}(n, k)$
, so
$\operatorname{SG}(n, k)$
, so
![]() $G_{u}$
is
$G_{u}$
is
![]() $\ell$
-colourable.
$\ell$
-colourable.
Now we consider a suitable blow-up of G. Let s be a multiple of n that is much larger than
![]() $\mathopen{}\left\vert \operatorname{SG}(n, k) \right\vert\mathclose{}$
. We will blow-up each
$\mathopen{}\left\vert \operatorname{SG}(n, k) \right\vert\mathclose{}$
. We will blow-up each
![]() $v_{i, i + 1}$
by
$v_{i, i + 1}$
by
![]() $s/n$
so that all rectangles contain s vertices, and we will blow up v by s also. Note that v together with the rectangles form a complete
$s/n$
so that all rectangles contain s vertices, and we will blow up v by s also. Note that v together with the rectangles form a complete
![]() $\ell$
-partite graph with s vertices in each part. Keep the copy of
$\ell$
-partite graph with s vertices in each part. Keep the copy of
![]() $\operatorname{SG}(n, k)$
as it is. Call the resulting graph
$\operatorname{SG}(n, k)$
as it is. Call the resulting graph
![]() $G^{\prime}$
.
$G^{\prime}$
.
-
G
 $^{\prime}$
has
$^{\prime}$
has
 $\ell s + \mathopen{}\left\vert \operatorname{SG}(n, k) \right\vert\mathclose{}$
vertices.
$\ell s + \mathopen{}\left\vert \operatorname{SG}(n, k) \right\vert\mathclose{}$
vertices. -
Any
 $A \in \operatorname{SG}(n, k)$
is adjacent to
$A \in \operatorname{SG}(n, k)$
is adjacent to
 $2k/n$
proportion of the
$2k/n$
proportion of the
 $v_{i, i + 1}$
so has degree at least
$v_{i, i + 1}$
so has degree at least
 $(\ell - 1) s (2k)/n = (\ell - 1)s/(1 + f(k)/(2k))$
.
$(\ell - 1) s (2k)/n = (\ell - 1)s/(1 + f(k)/(2k))$
. -
Any other vertex has degree at least
 $(\ell - 1) s$
.
$(\ell - 1) s$
. -
 $\chi(G') \geqslant \chi(\operatorname{SG}(n, k)) = n - 2k + 2 = f(k) + 2$
.
$\chi(G') \geqslant \chi(\operatorname{SG}(n, k)) = n - 2k + 2 = f(k) + 2$
.
Given any
![]() $C, \varepsilon > 0$
, we may choose k large enough so that
$C, \varepsilon > 0$
, we may choose k large enough so that
![]() $f(k) \geqslant C$
and
$f(k) \geqslant C$
and
![]() $(\ell - 1)/(1 + f(k)/(2k)) \geqslant \ell - 1 - \varepsilon$
and then choose s large enough so that
$(\ell - 1)/(1 + f(k)/(2k)) \geqslant \ell - 1 - \varepsilon$
and then choose s large enough so that
![]() $\ell s + \mathopen{}\left\vert \operatorname{SG}(n, k) \right\vert\mathclose{} \leqslant (\ell + \varepsilon) s$
. The resulting graph
$\ell s + \mathopen{}\left\vert \operatorname{SG}(n, k) \right\vert\mathclose{} \leqslant (\ell + \varepsilon) s$
. The resulting graph
![]() $G^{\prime}$
has chromatic number at least
$G^{\prime}$
has chromatic number at least
![]() $f(k) + 2 \geqslant C$
and
$f(k) + 2 \geqslant C$
and
Being a-locally b-partite is preserved when taking blow-ups. Now G is locally
![]() $\ell$
-partite and so
$\ell$
-partite and so
![]() $G^{\prime}$
is too. As
$G^{\prime}$
is too. As
![]() $\mathcal{F}_{1, \ell} \subset \mathcal{F}_{a, b}$
,
$\mathcal{F}_{1, \ell} \subset \mathcal{F}_{a, b}$
,
![]() $G^{\prime}$
is a-locally b-partite. Thus,
$G^{\prime}$
is a-locally b-partite. Thus,
but
![]() $\varepsilon > 0$
was arbitrary and so we have the required result.
$\varepsilon > 0$
was arbitrary and so we have the required result.
3 Structure of locally bipartite graphs down to
 $8/15$
$8/15$
Our understanding of the structure of locally bipartite graphs can be summarised as follows. The graphs
![]() $\overline{C}_{7}$
,
$\overline{C}_{7}$
,
![]() $H_{2}^{+}$
,
$H_{2}^{+}$
,
![]() $H_{2}$
, etc. can be seen in Figure 2 where they are discussed more thoroughly.
$H_{2}$
, etc. can be seen in Figure 2 where they are discussed more thoroughly.

Figure 1. In this diagram,
![]() $\ell = 5$
.
$\ell = 5$
.
Theorem 3.1. (locally bipartite graphs) Let G be a locally bipartite graph.
-
a. If
 $\delta(G) > 4/7 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is 3-colourable.
$\delta(G) > 4/7 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is 3-colourable. -
b. If
 $\delta(G) > 5/9 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is homomorphic to
$\delta(G) > 5/9 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is homomorphic to
 $\overline{C}_{7}$
. Also, G is either 3-colourable or contains
$\overline{C}_{7}$
. Also, G is either 3-colourable or contains
 $\overline{C}_{7}$
.
$\overline{C}_{7}$
. -
c. There is an absolute constant
 $\varepsilon > 0$
such that if
$\varepsilon > 0$
such that if
 $\delta(G) > (5/9 - \varepsilon) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is homomorphic to either
$\delta(G) > (5/9 - \varepsilon) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is homomorphic to either
 $\overline{C}_{7}$
or
$\overline{C}_{7}$
or
 $H_{2}^{+}$
.
$H_{2}^{+}$
. -
d. If
 $\delta(G) > 6/11 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is 4-colourable. Also, G is either 3-colourable or contains
$\delta(G) > 6/11 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is 4-colourable. Also, G is either 3-colourable or contains
 $\overline{C}_{7}$
or
$\overline{C}_{7}$
or
 $H_{2}^{+}$
. In the first two cases, G is homomorphic to
$H_{2}^{+}$
. In the first two cases, G is homomorphic to
 $\overline{C}_{7}$
.
$\overline{C}_{7}$
. -
e. If
 $\delta(G) > 7/13 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is either 3-colourable or contains
$\delta(G) > 7/13 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is either 3-colourable or contains
 $H_{2}$
.
$H_{2}$
. -
f. If
 $\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is either 3-colourable or contains
$\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is either 3-colourable or contains
 $H_{2}$
or
$H_{2}$
or
 $T_{0}$
.
$T_{0}$
.
In [Reference Illingworth11], we considered the structure of locally bipartite graphs with minimum degree down to
![]() $6/11,$
and, indeed, the first four parts of Theorem 3.1 are proved there. The purpose of this section is to prove the final two parts. In Section 3.1, we motivate this proof and also show that many of the constants in the theorem are tight.
$6/11,$
and, indeed, the first four parts of Theorem 3.1 are proved there. The purpose of this section is to prove the final two parts. In Section 3.1, we motivate this proof and also show that many of the constants in the theorem are tight.

Figure 2. The graphs of Theorem 3.1.
Figure 2 displays the graphs of Theorem 3.1 as well as some that appear in the proof.
-
All graphs shown are 4-chromatic, and all bar
 $W_{7}$
are locally bipartite.
$W_{7}$
are locally bipartite. -
The graph
 $H_{0}$
is isomorphic to the Moser Spindle – the smallest 4-chromatic unit distance graph.
$H_{0}$
is isomorphic to the Moser Spindle – the smallest 4-chromatic unit distance graph.
 $H_{0}$
is also the smallest 4-chromatic locally bipartite graph, and so it is natural that it should play such an integral part in many of our results. The graph
$H_{0}$
is also the smallest 4-chromatic locally bipartite graph, and so it is natural that it should play such an integral part in many of our results. The graph
 $\overline{C}_{7}$
is the complement (and also the square) of the 7-cycle.
$\overline{C}_{7}$
is the complement (and also the square) of the 7-cycle. -
Adding a single edge to
 $H_{0}$
while maintaining local bipartiteness can give rise to two non-isomorphic graphs, one of which is
$H_{0}$
while maintaining local bipartiteness can give rise to two non-isomorphic graphs, one of which is
 $H_{1}$
. The other will appear fleetingly in the proof of Claim 3.9. Adding a single edge to
$H_{1}$
. The other will appear fleetingly in the proof of Claim 3.9. Adding a single edge to
 $H_{1}$
while maintaining local bipartiteness gives rise to a unique (up to isomorphism) graph –
$H_{1}$
while maintaining local bipartiteness gives rise to a unique (up to isomorphism) graph –
 $H_{2}$
. There is only one way to add a single edge to
$H_{2}$
. There is only one way to add a single edge to
 $H_{2}$
and maintain local bipartiteness – this gives
$H_{2}$
and maintain local bipartiteness – this gives
 $\overline{C}_{7}$
.
$\overline{C}_{7}$
.
 $H_{2}^{+}$
is
$H_{2}^{+}$
is
 $H_{2}$
with a degree 3 vertex added.
$H_{2}$
with a degree 3 vertex added.
 $H_{1}^{++}$
is
$H_{1}^{++}$
is
 $H_{1}$
with two degree 3 vertices added.
$H_{1}$
with two degree 3 vertices added. -
 $\overline{C}_{7}$
and
$\overline{C}_{7}$
and
 $H_{2}^{+}$
are both edge-maximal locally bipartite graphs.
$H_{2}^{+}$
are both edge-maximal locally bipartite graphs. -
 $T_{0}$
is a 7-cycle (the outer cycle) together with two vertices each joined to six of the seven vertices in the outer cycle (with the ‘seventh’ vertices two apart) and finally a vertex of degree three is added.
$T_{0}$
is a 7-cycle (the outer cycle) together with two vertices each joined to six of the seven vertices in the outer cycle (with the ‘seventh’ vertices two apart) and finally a vertex of degree three is added. -
 $W_{7}$
, is called the 7-wheel. More generally, a single vertex joined to all the vertices of a k-cycle is called a k-wheel and is denoted by
$W_{7}$
, is called the 7-wheel. More generally, a single vertex joined to all the vertices of a k-cycle is called a k-wheel and is denoted by
 $W_{k}$
. We term any edge from the central vertex to the cycle a spoke of the wheel and any edge of the cycle a rim of the wheel. Note that a graph is locally bipartite exactly if it does not contain any odd wheel (there is no such nice characterisation for a graph being locally tripartite, locally 4-partite, …).
$W_{k}$
. We term any edge from the central vertex to the cycle a spoke of the wheel and any edge of the cycle a rim of the wheel. Note that a graph is locally bipartite exactly if it does not contain any odd wheel (there is no such nice characterisation for a graph being locally tripartite, locally 4-partite, …).
The following observation gives a useful link between local bipartiteness and some of these graphs. We will use it frequently when copies of
![]() $H_{0}$
,
$H_{0}$
,
![]() $H_{1}$
,
$H_{1}$
,
![]() $H_{2}$
or
$H_{2}$
or
![]() $\overline{C}_{7}$
appear.
$\overline{C}_{7}$
appear.
Remark 3.2. Any five vertices of
![]() $H_{0}$
contain a triangle or a 5-cycle. In particular, if G is a locally bipartite graph, then any vertex can have at most four neighbours in any copy of
$H_{0}$
contain a triangle or a 5-cycle. In particular, if G is a locally bipartite graph, then any vertex can have at most four neighbours in any copy of
![]() $H_{0}$
appearing in G.
$H_{0}$
appearing in G.
Containment and homomorphisms between the first seven graphs of Figure 2 are summarised in Figure 3. Note that a full arrow pointing from H to G signifies that H is a subgraph of G and a dashed arrow from H to G signifies that H is homomorphic to G. Furthermore, for two graphs H and G in the diagram, H is homomorphic to G exactly if there is a sequence of arrows starting at H and ending at G. We verify Figure 3 in the appendix.

Figure 3. Full arrows denote containment, dashed arrows denote homomorphisms.

Figure 4. Weightings of
![]() $H^{+}_{2}$, $H_{2}$, $T_{0}$
and
$H^{+}_{2}$, $H_{2}$, $T_{0}$
and
![]() $H^{++}_{1}$
.
$H^{++}_{1}$
.
3.1 The components of Theorem 3.1 and initial observations
We will start by noting which parts of Theorem 3.1 are tight. We will need suitable blow-ups of some of the graphs in Figure 2. In Figure 4 we give these blow-ups which have been chosen so that the ratio between the minimum degree and order of the graph is as large as possible. When we ‘weight a vertex by
![]() $0^{+}$
’, we are actually giving it some tiny positive weight (we have not deleted the vertices entirely just given them a small weight relative to the rest).
$0^{+}$
’, we are actually giving it some tiny positive weight (we have not deleted the vertices entirely just given them a small weight relative to the rest).
Now we address one-by-one the tightness of the constants in Theorem 3.1. First note that
![]() $\overline{C}_{7}$
is locally bipartite, 4-regular with 7 vertices and chromatic number 4. Hence, balanced blow-ups of
$\overline{C}_{7}$
is locally bipartite, 4-regular with 7 vertices and chromatic number 4. Hence, balanced blow-ups of
![]() $\overline{C}_{7}$
show that
$\overline{C}_{7}$
show that
![]() $4/7$
is tight in part a. Figure 4 shows that there are n-vertex blow-ups of
$4/7$
is tight in part a. Figure 4 shows that there are n-vertex blow-ups of
![]() $H_{2}^{+}$
with minimum degree at least
$H_{2}^{+}$
with minimum degree at least
![]() $5/9 \cdot n - \mathcal{O}(1)$
. These blow-ups of
$5/9 \cdot n - \mathcal{O}(1)$
. These blow-ups of
![]() $H_{2}^{+}$
are 4-chromatic (as
$H_{2}^{+}$
are 4-chromatic (as
![]() $H_{2}^{+}$
is), do not contain
$H_{2}^{+}$
is), do not contain
![]() $\overline{C}_{7}$
nor are homomorphic to
$\overline{C}_{7}$
nor are homomorphic to
![]() $\overline{C}_{7}$
(as neither of
$\overline{C}_{7}$
(as neither of
![]() $\overline{C}_{7}$
nor
$\overline{C}_{7}$
nor
![]() $H_{2}^{+}$
is homomorphic to the other). This gives the tightness of
$H_{2}^{+}$
is homomorphic to the other). This gives the tightness of
![]() $5/9$
in part b. Figure 4 shows that there are n-vertex blow-ups of
$5/9$
in part b. Figure 4 shows that there are n-vertex blow-ups of
![]() $H_{2}$
with minimum degree
$H_{2}$
with minimum degree
![]() $\lfloor 6/11 \cdot n \rfloor$
. These blow-ups are 4-chromatic and contain neither
$\lfloor 6/11 \cdot n \rfloor$
. These blow-ups are 4-chromatic and contain neither
![]() $\overline{C}_{7}$
nor
$\overline{C}_{7}$
nor
![]() $H_{2}^{+}$
, since neither of these is homomorphic to
$H_{2}^{+}$
, since neither of these is homomorphic to
![]() $H_{2}$
. Hence, in part d,
$H_{2}$
. Hence, in part d,
![]() $6/11$
is tight for the conclusion that G is either 3-colourable or contains
$6/11$
is tight for the conclusion that G is either 3-colourable or contains
![]() $\overline{C}_{7}$
or
$\overline{C}_{7}$
or
![]() $H_{2}^{+}$
. Tightness is not known for 4-colourability, and in fact, it seems likely that
$H_{2}^{+}$
. Tightness is not known for 4-colourability, and in fact, it seems likely that
![]() $\delta_{\chi}(\mathcal{F}_{1, 2}, 4) < 6/11$
. Similar arguments show that the weightings of
$\delta_{\chi}(\mathcal{F}_{1, 2}, 4) < 6/11$
. Similar arguments show that the weightings of
![]() $T_{0}$
and
$T_{0}$
and
![]() $H_{1}^{++}$
in Figure 4 give the tightness of
$H_{1}^{++}$
in Figure 4 give the tightness of
![]() $7/13$
and
$7/13$
and
![]() $8/15$
in parts e and f respectively.
$8/15$
in parts e and f respectively.
Our second aim in this section is to motivate the proof of parts e and f of Theorem 3.1. We will deduce them from the following two theorems.
Theorem 3.3. Let G be a locally bipartite graph. If
![]() $\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is either 3-colourable or contains
$\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is either 3-colourable or contains
![]() $H_{0}$
or
$H_{0}$
or
![]() $T_{0}$
. If
$T_{0}$
. If
![]() $\delta(G) > 7/13 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is either 3-colourable or contains
$\delta(G) > 7/13 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is either 3-colourable or contains
![]() $H_{0}$
.
$H_{0}$
.
Theorem 3.4. Let G be a locally bipartite graph that contains
![]() $H_{0}$
. If
$H_{0}$
. If
![]() $\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G contains
$\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G contains
![]() $H_{2}$
.
$H_{2}$
.
Proof of parts e and f. Let G be a locally bipartite graph. If
![]() $\delta(G) > 7/13 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then, by Theorem 3.3, G is either 3-colourable or contains
$\delta(G) > 7/13 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then, by Theorem 3.3, G is either 3-colourable or contains
![]() $H_{0}$
. If G contains
$H_{0}$
. If G contains
![]() $H_{0}$
, then Theorem 3.4 shows it actually contains
$H_{0}$
, then Theorem 3.4 shows it actually contains
![]() $H_{2}$
. This gives part e. Suppose instead that
$H_{2}$
. This gives part e. Suppose instead that
![]() $\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. By Theorem 3.3, G is either 3-colourable, contains
$\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. By Theorem 3.3, G is either 3-colourable, contains
![]() $T_{0}$
or contains
$T_{0}$
or contains
![]() $H_{0}$
. In the last case Theorem 3.4 shows that G contains
$H_{0}$
. In the last case Theorem 3.4 shows that G contains
![]() $H_{2}$
and so we have part f.
$H_{2}$
and so we have part f.
We prove Theorem 3.4 in Section 3.2 by counting edges between the copy of
![]() $H_{0}$
and G. Theorem 3.3 is more involved. As motivation, consider a locally bipartite
$H_{0}$
and G. Theorem 3.3 is more involved. As motivation, consider a locally bipartite
![]() $H_{2}$
-free G with
$H_{2}$
-free G with
![]() $\delta(G) > 7/13 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
(we will ignore the
$\delta(G) > 7/13 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
(we will ignore the
![]() $8/15$
conclusion here). By Theorem 3.4, G is
$8/15$
conclusion here). By Theorem 3.4, G is
![]() $H_{0}$
-free and our aim is to show that G is 3-colourable. We may as well assume that G is edge-maximal: the addition of any edge will give a copy of
$H_{0}$
-free and our aim is to show that G is 3-colourable. We may as well assume that G is edge-maximal: the addition of any edge will give a copy of
![]() $H_{0}$
or a vertex with non-bipartite neighbourhood. Thus, any non-edge of G is either the missing edge of a
$H_{0}$
or a vertex with non-bipartite neighbourhood. Thus, any non-edge of G is either the missing edge of a
![]() $K_{4}$
, a missing rim of an odd wheel, a missing spoke of an odd wheel or a missing edge of an
$K_{4}$
, a missing rim of an odd wheel, a missing spoke of an odd wheel or a missing edge of an
![]() $H_{0}$
. This motivates a key definition that also appeared in [Reference Illingworth11]. Recall that
$H_{0}$
. This motivates a key definition that also appeared in [Reference Illingworth11]. Recall that
![]() $G_{u, v}$
denotes the subgraph of G induced by the common neighbourhood of vertices u, v.
$G_{u, v}$
denotes the subgraph of G induced by the common neighbourhood of vertices u, v.
Definition 3.5. (dense and sparse) A pair of non-adjacent, distinct vertices u, v in a graph G is dense if
![]() $G_{u, v}$
contains an edge and sparse if
$G_{u, v}$
contains an edge and sparse if
![]() $G_{u, v}$
does not contain an edge.
$G_{u, v}$
does not contain an edge.
First note that every pair of distinct vertices in any graph is exactly one of ‘adjacent’, ‘dense’ or ‘sparse’. Another way to view being dense is as being the missing edge of a
![]() $K_{4}$
. Locally bipartite graphs are
$K_{4}$
. Locally bipartite graphs are
![]() $K_{4}$
-free so any pair of distinct vertices with an edge in their common neighbourhood must be non-adjacent and so dense. Our initial observations above show that each sparse pair of vertices in G is either the missing rim or spoke of an odd wheel or a missing edge of an
$K_{4}$
-free so any pair of distinct vertices with an edge in their common neighbourhood must be non-adjacent and so dense. Our initial observations above show that each sparse pair of vertices in G is either the missing rim or spoke of an odd wheel or a missing edge of an
![]() $H_{0}$
. In Section 3.3, we will rule out sparse pairs of vertices being the missing spoke of an odd wheel, and in Section 3.4, we will finish the proof by showing that G is 3-colourable.
$H_{0}$
. In Section 3.3, we will rule out sparse pairs of vertices being the missing spoke of an odd wheel, and in Section 3.4, we will finish the proof by showing that G is 3-colourable.
The distinction between dense and sparse pairs turns out to be crucial. We borrow from [Reference Illingworth11] the following three simple but useful lemmas. The final one hints at the importance of
![]() $H_{0}$
.
$H_{0}$
.
Lemma 3.6. Let G be a graph with
![]() $\delta(G) > 1/2 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and let I be any largest independent set in G. Then, for every distinct
$\delta(G) > 1/2 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and let I be any largest independent set in G. Then, for every distinct
![]() $u, v \in I$
, the pair u, v is dense.
$u, v \in I$
, the pair u, v is dense.
Lemma 3.7. Let G be a graph with
![]() $\delta(G) > 1/2 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and suppose C is an induced 4-cycle in G. Then at least one of the non-edges of C is a dense pair.
$\delta(G) > 1/2 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and suppose C is an induced 4-cycle in G. Then at least one of the non-edges of C is a dense pair.
Lemma 3.8. Let G be a locally bipartite graph which does not contain
![]() $H_{0}$
. For any vertex v of G,
$H_{0}$
. For any vertex v of G,
is an independent set of vertices.
3.2 From
 $H_{0}$
to
$H_{0}$
to
 $H_{2}$
– proof of Theorem 3.4
$H_{2}$
– proof of Theorem 3.4
In this subsection, we prove Theorem 3.4 in two steps. The strategy is to start with a copy of
![]() $H_{0}$
and consider edges between it and the rest of G. Using the high minimum degree, we are able to find a vertex with the correct neighbours in the copy of
$H_{0}$
and consider edges between it and the rest of G. Using the high minimum degree, we are able to find a vertex with the correct neighbours in the copy of
![]() $H_{0}$
so that a copy of
$H_{0}$
so that a copy of
![]() $H_{1}$
is present. We then play the same game to get a copy of
$H_{1}$
is present. We then play the same game to get a copy of
![]() $H_{2}$
. To aid the reader, we will use ‘
$H_{2}$
. To aid the reader, we will use ‘
![]() $G[v_{1}, v_{2}, \dotsc, v_{7}]$
is a copy of
$G[v_{1}, v_{2}, \dotsc, v_{7}]$
is a copy of
![]() $H_{1}$
’ to mean that G has a copy of
$H_{1}$
’ to mean that G has a copy of
![]() $H_{1}$
in which
$H_{1}$
in which
![]() $v_{1}$
is the top vertex (as displayed in Figure 2) and
$v_{1}$
is the top vertex (as displayed in Figure 2) and
![]() $v_{1}$
,
$v_{1}$
,
![]() $v_{2}$
, …,
$v_{2}$
, …,
![]() $v_{7}$
precede anticlockwise round the figure. We do similarly for copies of
$v_{7}$
precede anticlockwise round the figure. We do similarly for copies of
![]() $H_{2}$
.
$H_{2}$
.
Claim 3.9. Let G be a locally bipartite graph containing
![]() $H_{0}$
. If
$H_{0}$
. If
![]() $\delta(G) > 1/2 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G contains
$\delta(G) > 1/2 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G contains
![]() $H_{1}$
.
$H_{1}$
.
Proof. We label a copy of
![]() $H_{0}$
in G as below and let
$H_{0}$
in G as below and let
![]() $X = \mathopen{}\left\{a_{0}, a_{1}, \dotsc, a_{6}\right\}\mathclose{}$
.
$X = \mathopen{}\left\{a_{0}, a_{1}, \dotsc, a_{6}\right\}\mathclose{}$
.

Let
![]() $U_{4}$
be the set of vertices with exactly four neighbours in X. Remark 3.2 shows that no vertex has five neighbours in a copy of
$U_{4}$
be the set of vertices with exactly four neighbours in X. Remark 3.2 shows that no vertex has five neighbours in a copy of
![]() $H_{0}$
, so every non-
$H_{0}$
, so every non-
![]() $U_{4}$
vertex has at most three neighbours in X. Hence,
$U_{4}$
vertex has at most three neighbours in X. Hence,
and so
Now
![]() $\mathopen{}\left\vert U_{4} \right\vert\mathclose{} + d(a_{0}) > \mathopen{}\left\vert G \right\vert\mathclose{}$
and so some vertex v is adjacent to
$\mathopen{}\left\vert U_{4} \right\vert\mathclose{} + d(a_{0}) > \mathopen{}\left\vert G \right\vert\mathclose{}$
and so some vertex v is adjacent to
![]() $a_{0}$
and has exactly four neighbours in X. Note that v cannot be adjacent to both
$a_{0}$
and has exactly four neighbours in X. Note that v cannot be adjacent to both
![]() $a_{1}$
,
$a_{1}$
,
![]() $a_{2}$
as otherwise
$a_{2}$
as otherwise
![]() $va_{0}a_{1}a_{2}$
is a
$va_{0}a_{1}a_{2}$
is a
![]() $K_{4}$
, so by symmetry we may assume that v is not adjacent to
$K_{4}$
, so by symmetry we may assume that v is not adjacent to
![]() $a_{1}$
. Similarly, we may assume that v is not adjacent to
$a_{1}$
. Similarly, we may assume that v is not adjacent to
![]() $a_{5}$
. But v has four neighbours in X so must be adjacent to at least one of
$a_{5}$
. But v has four neighbours in X so must be adjacent to at least one of
![]() $a_{2}$
,
$a_{2}$
,
![]() $a_{6}$
– by symmetry, we may assume v is adjacent to
$a_{6}$
– by symmetry, we may assume v is adjacent to
![]() $a_{2}$
.
$a_{2}$
.
There are two possibilities: v is adjacent to
![]() $a_{0}, a_{2}, a_{3}, a_{4}$
, or v is adjacent to
$a_{0}, a_{2}, a_{3}, a_{4}$
, or v is adjacent to
![]() $a_{0}, a_{2}, a_{6}$
and one of
$a_{0}, a_{2}, a_{6}$
and one of
![]() $a_{3}$
,
$a_{3}$
,
![]() $a_{4}$
. In the latter case, we may assume by symmetry that v is adjacent to
$a_{4}$
. In the latter case, we may assume by symmetry that v is adjacent to
![]() $a_{3}$
. Hence, there are two possibilities for
$a_{3}$
. Hence, there are two possibilities for
![]() $\Gamma(v) \cap X$
:
$\Gamma(v) \cap X$
:
![]() $\mathopen{}\left\{a_{0}, a_{2}, a_{3}, a_{4}\right\}\mathclose{}$
and
$\mathopen{}\left\{a_{0}, a_{2}, a_{3}, a_{4}\right\}\mathclose{}$
and
![]() $\mathopen{}\left\{a_{0}, a_{2}, a_{3}, a_{6}\right\}\mathclose{}$
. In both cases, v cannot be any
$\mathopen{}\left\{a_{0}, a_{2}, a_{3}, a_{6}\right\}\mathclose{}$
. In both cases, v cannot be any
![]() $a_{i}$
except for possibly
$a_{i}$
except for possibly
![]() $a_{1}$
.
$a_{1}$
.
If
![]() $\Gamma(v) \cap X = \mathopen{}\left\{a_{0}, a_{2}, a_{3}, a_{4}\right\}\mathclose{}$
, then
$\Gamma(v) \cap X = \mathopen{}\left\{a_{0}, a_{2}, a_{3}, a_{4}\right\}\mathclose{}$
, then
![]() $G[v, a_{3}, a_{4}, a_{5}, a_{6}, a_{0}, a_{2}]$
is a copy of
$G[v, a_{3}, a_{4}, a_{5}, a_{6}, a_{0}, a_{2}]$
is a copy of
![]() $H_{1}$
. If
$H_{1}$
. If
![]() $\Gamma(v) \cap X = \mathopen{}\left\{a_{0}, a_{2}, a_{3}, a_{6}\right\}\mathclose{}$
, then G contains the following graph where, in particular, v is not adjacent to
$\Gamma(v) \cap X = \mathopen{}\left\{a_{0}, a_{2}, a_{3}, a_{6}\right\}\mathclose{}$
, then G contains the following graph where, in particular, v is not adjacent to
![]() $a_{4}$
.
$a_{4}$
.

Vertex
![]() $a_{6}$
is not adjacent to
$a_{6}$
is not adjacent to
![]() $a_{3}$
else
$a_{3}$
else
![]() $G_{a_{6}}$
contains the 5-cycle
$G_{a_{6}}$
contains the 5-cycle
![]() $a_{0}va_{3}a_{4}a_{5}$
. Hence,
$a_{0}va_{3}a_{4}a_{5}$
. Hence,
![]() $va_{6}a_{4}a_{3}$
is an induced 4-cycle in G. By Lemma 3.7, at least one of the pairs
$va_{6}a_{4}a_{3}$
is an induced 4-cycle in G. By Lemma 3.7, at least one of the pairs
![]() $v, a_{4}$
and
$v, a_{4}$
and
![]() $a_{3}, a_{6}$
is dense. By symmetry, we may assume that
$a_{3}, a_{6}$
is dense. By symmetry, we may assume that
![]() $v, a_{4}$
is dense: let
$v, a_{4}$
is dense: let
![]() ${a^{\prime}_{2}}{a^{\prime}_{3}}$
be an edge in
${a^{\prime}_{2}}{a^{\prime}_{3}}$
be an edge in
![]() $G_{v, a_{4}}$
. Vertex v is not adjacent to
$G_{v, a_{4}}$
. Vertex v is not adjacent to
![]() $a_{5}$
, so
$a_{5}$
, so
![]() $a_{5}$
is neither
$a_{5}$
is neither
![]() ${a^{\prime}_{2}}$
nor
${a^{\prime}_{2}}$
nor
![]() ${a^{\prime}_{3}}$
. Note that
${a^{\prime}_{3}}$
. Note that
![]() $a_{0}$
is not adjacent to
$a_{0}$
is not adjacent to
![]() $a_{4}$
(else
$a_{4}$
(else
![]() $a_{0}a_{4}a_{5}a_{6}$
is a
$a_{0}a_{4}a_{5}a_{6}$
is a
![]() $K_{4}$
) and so
$K_{4}$
) and so
![]() $a_{0}$
is neither
$a_{0}$
is neither
![]() ${a^{\prime}_{2}}$
nor
${a^{\prime}_{2}}$
nor
![]() ${a^{\prime}_{3}}$
. If
${a^{\prime}_{3}}$
. If
![]() $a_{6} = {a^{\prime}_{2}}$
, then
$a_{6} = {a^{\prime}_{2}}$
, then
![]() $G_{a_{6}}$
contains the 5-cycle
$G_{a_{6}}$
contains the 5-cycle
![]() ${a^{\prime}_{3}}va_{0}a_{5}a_{4}$
, which is impossible. Similarly,
${a^{\prime}_{3}}va_{0}a_{5}a_{4}$
, which is impossible. Similarly,
![]() $a_{6} \neq {a^{\prime}_{3}}$
. Hence,
$a_{6} \neq {a^{\prime}_{3}}$
. Hence,
![]() ${a^{\prime}_{2}}, {a^{\prime}_{3}}$
are distinct from
${a^{\prime}_{2}}, {a^{\prime}_{3}}$
are distinct from
![]() $a_{4}, a_{5}, a_{6}, a_{0}, v$
and so
$a_{4}, a_{5}, a_{6}, a_{0}, v$
and so
![]() $G[a_{6}, a_{0}, v, {a^{\prime}_{2}}, {a^{\prime}_{3}}, a_{4}, a_{5}]$
is a copy of
$G[a_{6}, a_{0}, v, {a^{\prime}_{2}}, {a^{\prime}_{3}}, a_{4}, a_{5}]$
is a copy of
![]() $H_{1}$
.
$H_{1}$
.
Claim 3.10. Let G be a locally bipartite graph containing
![]() $H_{1}$
. If
$H_{1}$
. If
![]() $\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G contains
$\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G contains
![]() $H_{2}$
.
$H_{2}$
.
Proof. Consider a copy of
![]() $H_{1}$
with vertices
$H_{1}$
with vertices
![]() $X = \mathopen{}\left\{a_{0}, a_{1}, \dotsc, a_{6}\right\}\mathclose{}$
. We assign a weighting
$X = \mathopen{}\left\{a_{0}, a_{1}, \dotsc, a_{6}\right\}\mathclose{}$
. We assign a weighting
![]() $\omega \colon X \rightarrow \mathbb{Z}_{\geqslant 0}$
as shown in the diagram below, so, for example
$\omega \colon X \rightarrow \mathbb{Z}_{\geqslant 0}$
as shown in the diagram below, so, for example
![]() $\omega(a_{0}) = 2$
and
$\omega(a_{0}) = 2$
and
![]() $\omega(a_{1}) = 1$
(recall this notation from Section 1.1). We will often use diagrams to give weightings in this way. For each vertex
$\omega(a_{1}) = 1$
(recall this notation from Section 1.1). We will often use diagrams to give weightings in this way. For each vertex
![]() $v \in G$
, let f(v) be the total weight of the neighbours of v in X.
$v \in G$
, let f(v) be the total weight of the neighbours of v in X.

We will assume that G does not contain
![]() $H_{2}$
. We first show that any vertex v has
$H_{2}$
. We first show that any vertex v has
![]() $f(v) \leqslant 6$
and further that if
$f(v) \leqslant 6$
and further that if
![]() $f(v) = 6$
, then
$f(v) = 6$
, then
![]() $\Gamma(v) \cap X = \mathopen{}\left\{a_{1}, a_{2}, a_{5}, a_{6}\right\}\mathclose{}$
.
$\Gamma(v) \cap X = \mathopen{}\left\{a_{1}, a_{2}, a_{5}, a_{6}\right\}\mathclose{}$
.
Let v be a vertex with
![]() $f(v) \geqslant 6$
. No vertex has five neighbours in a copy of
$f(v) \geqslant 6$
. No vertex has five neighbours in a copy of
![]() $H_{1}$
(as noted in Remark 3.2), so v is adjacent to at most four of the
$H_{1}$
(as noted in Remark 3.2), so v is adjacent to at most four of the
![]() $a_{i}$
. Thus, v is adjacent to at least two of the vertices of weight two, that is, to at least two of
$a_{i}$
. Thus, v is adjacent to at least two of the vertices of weight two, that is, to at least two of
![]() $a_{0}$
,
$a_{0}$
,
![]() $a_{2}$
,
$a_{2}$
,
![]() $a_{5}$
. If v is adjacent to all of
$a_{5}$
. If v is adjacent to all of
![]() $a_{0}, a_{2}, a_{5}$
, then
$a_{0}, a_{2}, a_{5}$
, then
![]() $G_{a_{0}}$
contains the odd circuit
$G_{a_{0}}$
contains the odd circuit
![]() $va_{5}a_{6}a_{1}a_{2}$
. Thus, v is adjacent to exactly two of
$va_{5}a_{6}a_{1}a_{2}$
. Thus, v is adjacent to exactly two of
![]() $a_{0}$
,
$a_{0}$
,
![]() $a_{2}$
and
$a_{2}$
and
![]() $a_{5}$
.
$a_{5}$
.
Suppose v is adjacent to
![]() $a_{0}$
. By symmetry, we may assume that v is adjacent to
$a_{0}$
. By symmetry, we may assume that v is adjacent to
![]() $a_{2}$
but not to
$a_{2}$
but not to
![]() $a_{5}$
. Then,v is not adjacent to
$a_{5}$
. Then,v is not adjacent to
![]() $a_{1}$
, else
$a_{1}$
, else
![]() $va_{0}a_{1}a_{2}$
is a
$va_{0}a_{1}a_{2}$
is a
![]() $K_{4}$
. Similarly, v cannot be adjacent to both
$K_{4}$
. Similarly, v cannot be adjacent to both
![]() $a_{3}$
and
$a_{3}$
and
![]() $a_{4}$
. Hence,v is adjacent to
$a_{4}$
. Hence,v is adjacent to
![]() $a_{0}$
,
$a_{0}$
,
![]() $a_{2}$
,
$a_{2}$
,
![]() $a_{6}$
and one of
$a_{6}$
and one of
![]() $a_{3}$
,
$a_{3}$
,
![]() $a_{4}$
. By symmetry, we may assume v is adjacent to
$a_{4}$
. By symmetry, we may assume v is adjacent to
![]() $a_{3}$
. Now v cannot be
$a_{3}$
. Now v cannot be
![]() $a_{4}$
nor
$a_{4}$
nor
![]() $a_{5}$
as it would then have five neighbours in X. Hence,
$a_{5}$
as it would then have five neighbours in X. Hence,
![]() $G[a_{5}, a_{6}, a_{0}, v, a_{2}, a_{3}, a_{4}]$
is a copy of
$G[a_{5}, a_{6}, a_{0}, v, a_{2}, a_{3}, a_{4}]$
is a copy of
![]() $H_{2}$
.
$H_{2}$
.
Thus, v is not adjacent to
![]() $a_{0}$
and so is adjacent to both
$a_{0}$
and so is adjacent to both
![]() $a_{2}$
and
$a_{2}$
and
![]() $a_{5}$
. Note v cannot be adjacent to both
$a_{5}$
. Note v cannot be adjacent to both
![]() $a_{3}$
,
$a_{3}$
,
![]() $a_{4}$
else
$a_{4}$
else
![]() $va_{2}a_{3}a_{4}$
is
$va_{2}a_{3}a_{4}$
is
![]() $K_{4}$
, so we may assume that v is adjacent to
$K_{4}$
, so we may assume that v is adjacent to
![]() $a_{1}$
. If v were adjacent to one of
$a_{1}$
. If v were adjacent to one of
![]() $a_{3}$
,
$a_{3}$
,
![]() $a_{4}$
, then we may assume by symmetry that v is adjacent to
$a_{4}$
, then we may assume by symmetry that v is adjacent to
![]() $a_{4}$
and not
$a_{4}$
and not
![]() $a_{3}$
. Now v cannot be
$a_{3}$
. Now v cannot be
![]() $a_{0}$
nor
$a_{0}$
nor
![]() $a_{6}$
as it would then have five neighbours in X. But then,
$a_{6}$
as it would then have five neighbours in X. But then,
![]() $G[a_{5}, a_{6}, a_{0}, a_{1}, a_{2}, v, a_{4}]$
is a copy of
$G[a_{5}, a_{6}, a_{0}, a_{1}, a_{2}, v, a_{4}]$
is a copy of
![]() $H_{2}$
. Therefore, v is adjacent to neither
$H_{2}$
. Therefore, v is adjacent to neither
![]() $a_{3}$
nor
$a_{3}$
nor
![]() $a_{4}$
. But
$a_{4}$
. But
![]() $f(v) \geqslant 6$
, so v is adjacent to
$f(v) \geqslant 6$
, so v is adjacent to
![]() $a_{1}$
,
$a_{1}$
,
![]() $a_{6}$
and thus
$a_{6}$
and thus
![]() $\Gamma(v) \cap X = \mathopen{}\left\{a_{1}, a_{2}, a_{5}, a_{6}\right\}\mathclose{}$
.
$\Gamma(v) \cap X = \mathopen{}\left\{a_{1}, a_{2}, a_{5}, a_{6}\right\}\mathclose{}$
.
So every vertex v has
![]() $f(v) \leqslant 6,$
and furthermore, all
$f(v) \leqslant 6,$
and furthermore, all
![]() $v \in \Gamma(a_{0}) \cup \Gamma(a_{3}) \cup \Gamma(a_{4})$
have
$v \in \Gamma(a_{0}) \cup \Gamma(a_{3}) \cup \Gamma(a_{4})$
have
![]() $f(v) \leqslant 5$
. We first claim that there is
$f(v) \leqslant 5$
. We first claim that there is
![]() $i \in \mathopen{}\left\{3, 4\right\}\mathclose{}$
such that
$i \in \mathopen{}\left\{3, 4\right\}\mathclose{}$
such that
![]() $\Gamma(a_{0}, a_{2}, a_{i}) = \varnothing$
. If not, there is
$\Gamma(a_{0}, a_{2}, a_{i}) = \varnothing$
. If not, there is
![]() ${a^{\prime}_{1}} \in \Gamma(a_{0}, a_{2}, a_{3})$
and
${a^{\prime}_{1}} \in \Gamma(a_{0}, a_{2}, a_{3})$
and
![]() ${a^{\prime\prime}_{1}} \in \Gamma(a_{0}, a_{2}, a_{4})$
. But then,
${a^{\prime\prime}_{1}} \in \Gamma(a_{0}, a_{2}, a_{4})$
. But then,
![]() $G_{a_{2}}$
contains the odd circuit
$G_{a_{2}}$
contains the odd circuit
![]() ${a^{\prime}_{1}} a_{3} a_{4} {a^{\prime\prime}_{1}} a_{0}$
. Similarly there is
${a^{\prime}_{1}} a_{3} a_{4} {a^{\prime\prime}_{1}} a_{0}$
. Similarly there is
![]() $j \in \mathopen{}\left\{3, 4\right\}\mathclose{}$
such that
$j \in \mathopen{}\left\{3, 4\right\}\mathclose{}$
such that
![]() $\Gamma(a_{0}, a_{5}, a_{j}) = \varnothing$
.
$\Gamma(a_{0}, a_{5}, a_{j}) = \varnothing$
.
Next we claim that there is
![]() $i \in \mathopen{}\left\{3, 4\right\}\mathclose{}$
with
$i \in \mathopen{}\left\{3, 4\right\}\mathclose{}$
with
![]() $\Gamma(a_{0}, a_{2}, a_{i}) = \Gamma(a_{0}, a_{5}, a_{i}) = \varnothing$
. If not, then without loss of generality there is
$\Gamma(a_{0}, a_{2}, a_{i}) = \Gamma(a_{0}, a_{5}, a_{i}) = \varnothing$
. If not, then without loss of generality there is
![]() ${a^{\prime}_{1}} \in \Gamma(a_{0}, a_{2}, a_{3})$
and
${a^{\prime}_{1}} \in \Gamma(a_{0}, a_{2}, a_{3})$
and
![]() ${a^{\prime}_{6}} \in \Gamma(a_{0}, a_{5}, a_{4})$
. Certainly,
${a^{\prime}_{6}} \in \Gamma(a_{0}, a_{5}, a_{4})$
. Certainly,
![]() $\Gamma({a^{\prime}_{1}}) \cap X \neq \mathopen{}\left\{a_{1}, a_{2}, a_{5}, a_{6}\right\}\mathclose{}$
, so
$\Gamma({a^{\prime}_{1}}) \cap X \neq \mathopen{}\left\{a_{1}, a_{2}, a_{5}, a_{6}\right\}\mathclose{}$
, so
![]() $f({a^{\prime}_{1}}) \leqslant 5$
. But
$f({a^{\prime}_{1}}) \leqslant 5$
. But
![]() $\omega(a_{0}) + \omega(a_{2}) + \omega(a_{3}) = 5$
, so
$\omega(a_{0}) + \omega(a_{2}) + \omega(a_{3}) = 5$
, so
![]() $\Gamma({a^{\prime}_{1}}) \cap X = \mathopen{}\left\{a_{0}, a_{2}, a_{3}\right\}\mathclose{}$
. Similarly
$\Gamma({a^{\prime}_{1}}) \cap X = \mathopen{}\left\{a_{0}, a_{2}, a_{3}\right\}\mathclose{}$
. Similarly
![]() $\Gamma({a^{\prime}_{6}}) \cap X = \mathopen{}\left\{a_{0}, a_{4}, a_{5}\right\}\mathclose{}$
. In particular, all of
$\Gamma({a^{\prime}_{6}}) \cap X = \mathopen{}\left\{a_{0}, a_{4}, a_{5}\right\}\mathclose{}$
. In particular, all of
![]() $a_{0}, \dotsc, a_{6}, {a^{\prime}_{1}}, {a^{\prime}_{6}}$
are distinct. But then,
$a_{0}, \dotsc, a_{6}, {a^{\prime}_{1}}, {a^{\prime}_{6}}$
are distinct. But then,
![]() $G[a_{0}, {a^{\prime}_{1}}, a_{2}, a_{3}, a_{4}, a_{5}, {a^{\prime}_{6}}]$
is a copy of
$G[a_{0}, {a^{\prime}_{1}}, a_{2}, a_{3}, a_{4}, a_{5}, {a^{\prime}_{6}}]$
is a copy of
![]() $H_{2}$
. Thus, without loss of generality,
$H_{2}$
. Thus, without loss of generality,
![]() $\Gamma(a_{0}, a_{2}, a_{3}) = \Gamma(a_{0}, a_{5}, a_{3}) = \varnothing$
. Then,
$\Gamma(a_{0}, a_{2}, a_{3}) = \Gamma(a_{0}, a_{5}, a_{3}) = \varnothing$
. Then,
![]() $\Gamma(a_{3})$
,
$\Gamma(a_{3})$
,
![]() $\Gamma(a_{0}, a_{2})$
,
$\Gamma(a_{0}, a_{2})$
,
![]() $\Gamma(a_{0}, a_{5})$
are pairwise disjoint (we already showed that
$\Gamma(a_{0}, a_{5})$
are pairwise disjoint (we already showed that
![]() $\Gamma(a_{0}, a_{2}, a_{5}) = \varnothing$
). Hence, the set
$\Gamma(a_{0}, a_{2}, a_{5}) = \varnothing$
). Hence, the set
![]() $Y = \Gamma(a_{3}) \cup \Gamma(a_{0}, a_{2}) \cup \Gamma(a_{0}, a_{5})$
has size
$Y = \Gamma(a_{3}) \cup \Gamma(a_{0}, a_{2}) \cup \Gamma(a_{0}, a_{5})$
has size
Now all
![]() $v \in Y$
have
$v \in Y$
have
![]() $f(v) \leqslant 5$
. We bound
$f(v) \leqslant 5$
. We bound
![]() $\omega(X, G)$
from both directions (recalling this notation from Section 1.1) to get
$\omega(X, G)$
from both directions (recalling this notation from Section 1.1) to get
which contradicts
![]() $\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
.
$\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
.
These two claims combine to give Theorem 3.4.
3.3 Ruling out sparse pairs being spokes of odd wheels
In this subsection, we make a start on the proof of Theorem 3.3, by ruling out the possibility that G contains a sparse pair of vertices which is the spoke of an odd wheel (Corollary 3.18). Our next three lemmas show that any sparse pair which is the missing spoke of an odd wheel is, in fact, the missing spoke of a 7-wheel. The following straightforward lemma appeared in [Reference Illingworth11].
Lemma 3.11. Let G be a locally bipartite graph with
![]() $\delta(G) > 1/2 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and which does not contain
$\delta(G) > 1/2 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and which does not contain
![]() $H_{0}$
. Then,G does not contain a sparse pair u, v with uv being the missing spoke of a 5-wheel.
$H_{0}$
. Then,G does not contain a sparse pair u, v with uv being the missing spoke of a 5-wheel.
We will use the following technical lemma on various occasions.
Lemma 3.12. Let G be a locally bipartite graph and let u, v be a sparse pair of vertices in G. Suppose that C is the shortest odd cycle which both passes through v and satisfies
![]() $C \setminus \mathopen{}\left\{v\right\}\mathclose{} \subset \Gamma(u)$
(i.e.
$C \setminus \mathopen{}\left\{v\right\}\mathclose{} \subset \Gamma(u)$
(i.e.
![]() $G[C \cup \mathopen{}\left\{u\right\}\mathclose{}]$
contains an odd wheel missing the spoke uv). Then, every neighbour of u has at most two neighbours in C and if two, then they are two apart on C. In particular, C is an induced cycle.
$G[C \cup \mathopen{}\left\{u\right\}\mathclose{}]$
contains an odd wheel missing the spoke uv). Then, every neighbour of u has at most two neighbours in C and if two, then they are two apart on C. In particular, C is an induced cycle.
Proof. Label the configuration as follows and write
![]() $v_{0}$
for v (we consider indices modulo
$v_{0}$
for v (we consider indices modulo
![]() $2k + 1$
). Note
$2k + 1$
). Note
![]() $C = \mathopen{}\left\{v, v_{1}, \dotsc, v_{2k}\right\}\mathclose{}$
.
$C = \mathopen{}\left\{v, v_{1}, \dotsc, v_{2k}\right\}\mathclose{}$
.

Consider a vertex x which is adjacent to u. Suppose that x is adjacent to two vertices in C which are not two apart: x is adjacent to
![]() $v_{i}$
and
$v_{i}$
and
![]() $v_{i + r}$
where
$v_{i + r}$
where
![]() $r \in \mathopen{}\left\{1, 3, 4, \dotsc, k\right\}\mathclose{}$
. Firstly, if
$r \in \mathopen{}\left\{1, 3, 4, \dotsc, k\right\}\mathclose{}$
. Firstly, if
![]() $r = 1$
, then either G contains the
$r = 1$
, then either G contains the
![]() $K_{4}$
$K_{4}$
![]() $uxv_{i}v_{i + 1}$
or
$uxv_{i}v_{i + 1}$
or
![]() $G_{u, v}$
contains an edge (if one of
$G_{u, v}$
contains an edge (if one of
![]() $v_{i}$
or
$v_{i}$
or
![]() $v_{i + 1}$
is v) which contradicts the sparsity of u, v. Secondly, if
$v_{i + 1}$
is v) which contradicts the sparsity of u, v. Secondly, if
![]() $r > 1$
is odd, then
$r > 1$
is odd, then
![]() $C' = x v_{i} v_{i + 1} \dotsb v_{i + r}$
is an odd circuit which is shorter than C. But then, C
$C' = x v_{i} v_{i + 1} \dotsb v_{i + r}$
is an odd circuit which is shorter than C. But then, C
![]() $^{\prime}$
contains an odd cycle
$^{\prime}$
contains an odd cycle
![]() $C^{\prime\prime}$
which is shorter than C. Either
$C^{\prime\prime}$
which is shorter than C. Either
![]() $C^{\prime\prime}$
is in
$C^{\prime\prime}$
is in
![]() $G_{u}$
(if
$G_{u}$
(if
![]() $v \not \in C''$
) contradicting the local bipartiteness of G or we have found a shorter odd cycle than C which satisfies the properties of C (if
$v \not \in C''$
) contradicting the local bipartiteness of G or we have found a shorter odd cycle than C which satisfies the properties of C (if
![]() $v \in C''$
). Finally, if
$v \in C''$
). Finally, if
![]() $r > 2$
is even, then
$r > 2$
is even, then
![]() $C' = xv_{i + r}v_{i + r + 1} \dotsb v_{i - 1} v_{i}$
is an odd circuit which is shorter than C. Again C
$C' = xv_{i + r}v_{i + r + 1} \dotsb v_{i - 1} v_{i}$
is an odd circuit which is shorter than C. Again C
![]() $^{\prime}$
must contain an odd cycle
$^{\prime}$
must contain an odd cycle
![]() $C^{\prime\prime}$
which is shorter than C. We either obtain an odd cycle in
$C^{\prime\prime}$
which is shorter than C. We either obtain an odd cycle in
![]() $G_{u}$
or contradict the minimality of C. Hence, every neighbour of u has at most two neighbours in C, and if two, then they are
$G_{u}$
or contradict the minimality of C. Hence, every neighbour of u has at most two neighbours in C, and if two, then they are
![]() $v_{i}$
,
$v_{i}$
,
![]() $v_{i + 2}$
for some i.
$v_{i + 2}$
for some i.
All of
![]() $v_{1}, \dotsc, v_{2k}$
are neighbours of u so have two neighbours in C. Hence, C is induced.
$v_{1}, \dotsc, v_{2k}$
are neighbours of u so have two neighbours in C. Hence, C is induced.
Lemma 3.13. Let G be a locally bipartite graph with
![]() $\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
which does not contain
$\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
which does not contain
![]() $H_{0}$
. Any sparse pair in G that is the missing spoke of an odd wheel is the missing spoke of a 7-wheel.
$H_{0}$
. Any sparse pair in G that is the missing spoke of an odd wheel is the missing spoke of a 7-wheel.
Proof. Consider a sparse pair u, v that is the missing spoke of a
![]() $(2k + 1)$
-wheel. Choose the odd wheel so that k is minimal. Without loss of generality, u is the central vertex and v is in the outer
$(2k + 1)$
-wheel. Choose the odd wheel so that k is minimal. Without loss of generality, u is the central vertex and v is in the outer
![]() $(2k + 1)$
-cycle which we call C. Lemma 3.11 shows that
$(2k + 1)$
-cycle which we call C. Lemma 3.11 shows that
![]() $k > 2$
. We are done if we can show that
$k > 2$
. We are done if we can show that
![]() $k = 3$
.
$k = 3$
.
By Lemma 3.12, every neighbour of u has at most two neighbours in C. All vertices have at most 2k neighbours in C as otherwise G contains a
![]() $(2k + 1)$
-wheel and so is not locally bipartite. Hence,
$(2k + 1)$
-wheel and so is not locally bipartite. Hence,
so
which implies that
![]() $k < 4$
.
$k < 4$
.
Thus, to rule out sparse pairs being a missing spoke of an odd wheel we only need to rule out there being a sparse pair which is the missing spoke of a 7-wheel. This is where the graph
![]() $T_{0}$
becomes relevant. We will prove the following.
$T_{0}$
becomes relevant. We will prove the following.
Proposition 3.14. Let G be a locally bipartite graph which does not contain
![]() $H_{0}$
. If either
$H_{0}$
. If either
![]() $\delta(G) > 7/13 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, or
$\delta(G) > 7/13 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, or
![]() $\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and G does not contain
$\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and G does not contain
![]() $T_{0}$
, then G does not contain a sparse pair that is the missing spoke of a 7-wheel.
$T_{0}$
, then G does not contain a sparse pair that is the missing spoke of a 7-wheel.
Proof. Let G be a locally bipartite graph which does not contain
![]() $H_{0}$
and either satisfies
$H_{0}$
and either satisfies
![]() $\delta(G) > 7/13 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, or
$\delta(G) > 7/13 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, or
![]() $\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and G does not contain
$\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and G does not contain
![]() $T_{0}$
. In a slight abuse of notation, we will say that a vertex u is sparse to a cycle C if u is adjacent to
$T_{0}$
. In a slight abuse of notation, we will say that a vertex u is sparse to a cycle C if u is adjacent to
![]() $\mathopen{}\left\vert C \right\vert\mathclose{} - 1$
vertices of C and is in a sparse pair with the final vertex. We are required to show that there is no vertex u and no 7-cycle C with u sparse to C.
$\mathopen{}\left\vert C \right\vert\mathclose{} - 1$
vertices of C and is in a sparse pair with the final vertex. We are required to show that there is no vertex u and no 7-cycle C with u sparse to C.
By Lemma 3.11, there is no 5-cycle C and vertex u with u sparse to C. Hence, if a vertex u is sparse to a 7-cycle C, then, by Lemma 3.12, C is an induced 7-cycle and any neighbour of u has at most two neighbours in C.
Claim 3.15. If a vertex u is sparse to a 7-cycle
![]() $C = v_{0}v_{1} \dotsc v_{6}$
with the pair
$C = v_{0}v_{1} \dotsc v_{6}$
with the pair
![]() $u, v_{0}$
sparse, then there is some vertex which has six neighbours in C and is adjacent to all of
$u, v_{0}$
sparse, then there is some vertex which has six neighbours in C and is adjacent to all of
![]() $v_{6}$
,
$v_{6}$
,
![]() $v_{0}$
,
$v_{0}$
,
![]() $v_{1}$
.
$v_{1}$
.
Proof of Claim. First consider the induced 4-cycle
![]() $uv_{6}v_{0}v_{1}$
. The pair
$uv_{6}v_{0}v_{1}$
. The pair
![]() $u, v_{0}$
is sparse, so
$u, v_{0}$
is sparse, so
![]() $\Gamma(u, v_{6}, v_{0}) = \Gamma(v_{0}, v_{1}, u) = \varnothing$
. Also
$\Gamma(u, v_{6}, v_{0}) = \Gamma(v_{0}, v_{1}, u) = \varnothing$
. Also
![]() $\Gamma(v_{1}, u, v_{6}) = \varnothing$
as otherwise
$\Gamma(v_{1}, u, v_{6}) = \varnothing$
as otherwise
![]() $G_{u}$
contains an odd circuit. Hence, all
$G_{u}$
contains an odd circuit. Hence, all
![]() $z \not \in \Gamma(v_{6}, v_{0}, v_{1})$
have at most two neighbours in
$z \not \in \Gamma(v_{6}, v_{0}, v_{1})$
have at most two neighbours in
![]() $\mathopen{}\left\{u, v_{6}, v_{0}, v_{1}\right\}\mathclose{}$
.
$\mathopen{}\left\{u, v_{6}, v_{0}, v_{1}\right\}\mathclose{}$
.

Thus,
so
![]() $\mathopen{}\left\vert \Gamma(v_{6}, v_{0}, v_{1}) \right\vert\mathclose{} \geqslant 4 \delta(G) - 2 \mathopen{}\left\vert G \right\vert\mathclose{}$
.
$\mathopen{}\left\vert \Gamma(v_{6}, v_{0}, v_{1}) \right\vert\mathclose{} \geqslant 4 \delta(G) - 2 \mathopen{}\left\vert G \right\vert\mathclose{}$
.
If the claim is false, then all vertices in
![]() $\Gamma(v_{6}, v_{0}, v_{1})$
have at most five neighbours in C. Also note that
$\Gamma(v_{6}, v_{0}, v_{1})$
have at most five neighbours in C. Also note that
![]() $\Gamma(u)$
and
$\Gamma(u)$
and
![]() $\Gamma(v_{6}, v_{0}, v_{1})$
are disjoint and that all vertices have at most six neighbours in C (otherwise G contains a 7-wheel) so,
$\Gamma(v_{6}, v_{0}, v_{1})$
are disjoint and that all vertices have at most six neighbours in C (otherwise G contains a 7-wheel) so,
which contradicts
![]() $\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
.
$\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
.
Claim 3.16. Let C be a 7-cycle such that there is some vertex which is sparse to C. Then, every vertex with at least six neighbours in C is sparse to C.
Proof of Claim. Let vertex u be sparse to the 7-cycle C and let x be a vertex with at least six neighbours in C. Since G is locally bipartite, x has exactly six neighbours in C. Let y be the vertex of C to which x is not adjacent. There is a vertex u
![]() $^{\prime}$
which has six neighbours in C and is adjacent to y. Indeed, if u is adjacent to y then take
$^{\prime}$
which has six neighbours in C and is adjacent to y. Indeed, if u is adjacent to y then take
![]() $u' = u$
and if u is not adjacent to y, then Claim 3.15 gives the desired u
$u' = u$
and if u is not adjacent to y, then Claim 3.15 gives the desired u
![]() $^{\prime}$
.
$^{\prime}$
.
Now
![]() $\Gamma(u',x)$
contains two consecutive vertices of C, so the pair u
$\Gamma(u',x)$
contains two consecutive vertices of C, so the pair u
![]() $^{\prime}$
, x is dense. But u
$^{\prime}$
, x is dense. But u
![]() $^{\prime}$
is adjacent to y so, by Lemma 3.8, the pair y, x cannot be dense. In particular, x, y is sparse and so x is sparse to C.
$^{\prime}$
is adjacent to y so, by Lemma 3.8, the pair y, x cannot be dense. In particular, x, y is sparse and so x is sparse to C.
Now fix a 7-cycle
![]() $C = v_{0} v_{1} \dotsc v_{6}$
such that there is some vertex which is sparse to C. Say vertex
$C = v_{0} v_{1} \dotsc v_{6}$
such that there is some vertex which is sparse to C. Say vertex
![]() $v_{i}$
is lonely if there is some vertex u which is adjacent to all of
$v_{i}$
is lonely if there is some vertex u which is adjacent to all of
![]() $C \setminus \mathopen{}\left\{v_{i}\right\}\mathclose{}$
– by the previous claim u is sparse to C and the pair
$C \setminus \mathopen{}\left\{v_{i}\right\}\mathclose{}$
– by the previous claim u is sparse to C and the pair
![]() $u, v_{i}$
is sparse.
$u, v_{i}$
is sparse.
Claim 3.17. For all i,
![]() $v_{i}$
and
$v_{i}$
and
![]() $v_{i + 2}$
are not both lonely.
$v_{i + 2}$
are not both lonely.
Proof of Claim. Suppose for contradiction that
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{6}$
are both lonely: let
$v_{6}$
are both lonely: let
![]() $u_{1}$
and
$u_{1}$
and
![]() $u_{6}$
be sparse to C with both the pairs
$u_{6}$
be sparse to C with both the pairs
![]() $u_{1}, v_{1}$
and
$u_{1}, v_{1}$
and
![]() $u_{6}, v_{6}$
sparse. Lemma 3.12 shows that any neighbour of
$u_{6}, v_{6}$
sparse. Lemma 3.12 shows that any neighbour of
![]() $u_{1}$
(or
$u_{1}$
(or
![]() $u_{6}$
) has at most two neighbours in C. Let
$u_{6}$
) has at most two neighbours in C. Let
![]() $X = \mathopen{}\left\{u_{1}, u_{6}, v_{0}, \dotsc, v_{6}\right\}\mathclose{}$
and give a weighting
$X = \mathopen{}\left\{u_{1}, u_{6}, v_{0}, \dotsc, v_{6}\right\}\mathclose{}$
and give a weighting
![]() $\omega$
to the vertices in X as shown below.
$\omega$
to the vertices in X as shown below.

For each vertex
![]() $v \in G$
, let f(v) be the total weight of the neighbours of v in X. We shall show that if
$v \in G$
, let f(v) be the total weight of the neighbours of v in X. We shall show that if
![]() $v \not \in \Gamma(u_{6}, u_{1}, v_{0})$
, then
$v \not \in \Gamma(u_{6}, u_{1}, v_{0})$
, then
![]() $f(v) \leqslant 10$
and if
$f(v) \leqslant 10$
and if
![]() $v \in \Gamma(u_{6}, u_{1}, v_{0})$
, then
$v \in \Gamma(u_{6}, u_{1}, v_{0})$
, then
![]() $f(v) = 13$
. Let v be a vertex with
$f(v) = 13$
. Let v be a vertex with
![]() $f(v) \geqslant 11$
. It suffices to show that v is adjacent to
$f(v) \geqslant 11$
. It suffices to show that v is adjacent to
![]() $u_{6}$
,
$u_{6}$
,
![]() $u_{1}$
,
$u_{1}$
,
![]() $v_{0}$
and none of
$v_{0}$
and none of
![]() $v_{1}$
, …,
$v_{1}$
, …,
![]() $v_{6}$
.
$v_{6}$
.
If v is adjacent to neither
![]() $u_{1}$
nor
$u_{1}$
nor
![]() $u_{6}$
, then
$u_{6}$
, then
![]() $f(v) \leqslant 11$
with equality only if v is adjacent to all of C which would give a 7-wheel so, in fact,
$f(v) \leqslant 11$
with equality only if v is adjacent to all of C which would give a 7-wheel so, in fact,
![]() $f(v) \leqslant 10$
. Thus, we may assume v is adjacent to
$f(v) \leqslant 10$
. Thus, we may assume v is adjacent to
![]() $u_{1}$
. But then, v must have at most two neighbours in C. If neither of these is
$u_{1}$
. But then, v must have at most two neighbours in C. If neither of these is
![]() $v_{0}$
, then
$v_{0}$
, then
![]() $f(v) \leqslant 4 + 4 + 1 + 1 = 10$
. Hence, we may assume v is adjacent to both
$f(v) \leqslant 4 + 4 + 1 + 1 = 10$
. Hence, we may assume v is adjacent to both
![]() $v_{0}$
and
$v_{0}$
and
![]() $u_{1}$
.
$u_{1}$
.
Since
![]() $f(v) \geqslant 11$
and v has at most two neighbours in C, v must be adjacent to
$f(v) \geqslant 11$
and v has at most two neighbours in C, v must be adjacent to
![]() $u_{6}$
as well. Now, v is adjacent to both
$u_{6}$
as well. Now, v is adjacent to both
![]() $u_{1}$
and
$u_{1}$
and
![]() $v_{0}$
so, by Lemma 3.12, the only other possible neighbour of v in C is one of
$v_{0}$
so, by Lemma 3.12, the only other possible neighbour of v in C is one of
![]() $v_{2}$
and
$v_{2}$
and
![]() $v_{5}$
. However, if v is adjacent to
$v_{5}$
. However, if v is adjacent to
![]() $v_{2}$
, then
$v_{2}$
, then
![]() $G_{u_{1}}$
contains the odd circuit
$G_{u_{1}}$
contains the odd circuit
![]() $v_{0}vv_{2}v_{3}\dotsc v_{6}$
while if v is adjacent to
$v_{0}vv_{2}v_{3}\dotsc v_{6}$
while if v is adjacent to
![]() $v_{5}$
, then
$v_{5}$
, then
![]() $G_{u_{6}}$
contains the odd circuit
$G_{u_{6}}$
contains the odd circuit
![]() $v_{0}v_{1}\dotsc v_{5}v$
. In conclusion, v is adjacent to
$v_{0}v_{1}\dotsc v_{5}v$
. In conclusion, v is adjacent to
![]() $u_{1}$
,
$u_{1}$
,
![]() $u_{6}$
,
$u_{6}$
,
![]() $v_{0}$
, and no other vertices of C.
$v_{0}$
, and no other vertices of C.
Thus,
so
Any
![]() $v \in \Gamma(v_{0}, u_{1}, u_{6})$
satisfies
$v \in \Gamma(v_{0}, u_{1}, u_{6})$
satisfies
![]() $f(v) = 13$
so has only one neighbour in C. Also any neighbour of
$f(v) = 13$
so has only one neighbour in C. Also any neighbour of
![]() $u_{1}$
has at most two neighbours in C. Hence,
$u_{1}$
has at most two neighbours in C. Hence,
so
Combining inequalities (1) and (2) gives
so
![]() $\delta(G) \leqslant 7/13 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and so G is
$\delta(G) \leqslant 7/13 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and so G is
![]() $T_{0}$
-free.
$T_{0}$
-free.
Inequality (1) and
![]() $\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
show that
$\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
show that
![]() $\Gamma(v_{0}, u_{1}, u_{6})$
is non-empty. Let v be a common neighbour of
$\Gamma(v_{0}, u_{1}, u_{6})$
is non-empty. Let v be a common neighbour of
![]() $v_{0}$
,
$v_{0}$
,
![]() $u_{1}$
,
$u_{1}$
,
![]() $u_{6}$
. As G is
$u_{6}$
. As G is
![]() $T_{0}$
-free, v must be one of the
$T_{0}$
-free, v must be one of the
![]() $v_{i}$
. But
$v_{i}$
. But
![]() $C = v_{0}v_{1} \dotsc v_{6}$
is induced, so v must be one of
$C = v_{0}v_{1} \dotsc v_{6}$
is induced, so v must be one of
![]() $v_{1}$
,
$v_{1}$
,
![]() $v_{6}$
. This means one of the edges
$v_{6}$
. This means one of the edges
![]() $u_{1}v_{1}$
,
$u_{1}v_{1}$
,
![]() $u_{6}v_{6}$
is present. However, these are both sparse pairs giving the required contradiction.
$u_{6}v_{6}$
is present. However, these are both sparse pairs giving the required contradiction.
We now finish the proof of Proposition 3.14. By the choice of C, some
![]() $v_{i}$
is lonely. Without loss of generality,
$v_{i}$
is lonely. Without loss of generality,
![]() $v_{0}$
is lonely. By Claim 3.17, neither
$v_{0}$
is lonely. By Claim 3.17, neither
![]() $v_{2}$
nor
$v_{2}$
nor
![]() $v_{5}$
is lonely. By Claims 3.15 and 3.16, at least one of
$v_{5}$
is lonely. By Claims 3.15 and 3.16, at least one of
![]() $v_{3}$
and
$v_{3}$
and
![]() $v_{4}$
is lonely. By Claim 3.17, we may assume
$v_{4}$
is lonely. By Claim 3.17, we may assume
![]() $v_{3}$
is lonely. By lonely,
$v_{3}$
is lonely. By lonely,
![]() $v_{1}$
is not lonely and at most one of
$v_{1}$
is not lonely and at most one of
![]() $v_{4}$
,
$v_{4}$
,
![]() $v_{6}$
is. Again, by symmetry, we may assume
$v_{6}$
is. Again, by symmetry, we may assume
![]() $v_{6}$
is not lonely. In conclusion,
$v_{6}$
is not lonely. In conclusion,
![]() $v_{1}$
,
$v_{1}$
,
![]() $v_{2}$
,
$v_{2}$
,
![]() $v_{5}$
,
$v_{5}$
,
![]() $v_{6}$
are all not lonely,
$v_{6}$
are all not lonely,
![]() $v_{0}$
and
$v_{0}$
and
![]() $v_{3}$
are lonely and
$v_{3}$
are lonely and
![]() $v_{4}$
may or may not be.
$v_{4}$
may or may not be.
Let
![]() $U_{6}$
be the set of vertices with six neighbours in C. By Claim 3.16, any vertex in
$U_{6}$
be the set of vertices with six neighbours in C. By Claim 3.16, any vertex in
![]() $U_{6}$
is sparse to C so cannot be adjacent to all of
$U_{6}$
is sparse to C so cannot be adjacent to all of
![]() $v_{0}$
,
$v_{0}$
,
![]() $v_{3}$
,
$v_{3}$
,
![]() $v_{4}$
(else some other
$v_{4}$
(else some other
![]() $v_{i}$
is lonely). In particular,
$v_{i}$
is lonely). In particular,
As
![]() $v_{0}$
is lonely, there is a vertex u that is sparse to C with
$v_{0}$
is lonely, there is a vertex u that is sparse to C with
![]() $u, v_{0}$
sparse. No two of
$u, v_{0}$
sparse. No two of
![]() $v_{0}, v_{3}, v_{4}$
are two apart on C and so, by Lemma 3.12, any neighbour of u is in at least two of
$v_{0}, v_{3}, v_{4}$
are two apart on C and so, by Lemma 3.12, any neighbour of u is in at least two of
![]() $\overline{\Gamma(v_{0})}$
,
$\overline{\Gamma(v_{0})}$
,
![]() $\overline{\Gamma(v_{3})}$
,
$\overline{\Gamma(v_{3})}$
,
![]() $\overline{\Gamma(v_{4})}$
and is not in
$\overline{\Gamma(v_{4})}$
and is not in
![]() $U_{6}$
. Hence
$U_{6}$
. Hence
and so
![]() $\mathopen{}\left\vert U_{6} \right\vert\mathclose{} \leqslant 3 \mathopen{}\left\vert G \right\vert\mathclose{} - 5 \delta(G)$
. Since every neighbour of u has at most two neighbours in C,
$\mathopen{}\left\vert U_{6} \right\vert\mathclose{} \leqslant 3 \mathopen{}\left\vert G \right\vert\mathclose{} - 5 \delta(G)$
. Since every neighbour of u has at most two neighbours in C,
which contradicts
![]() $\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
.
$\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
.
Lemmas 3.11 and 3.13 and Proposition 3.14 together give the result we need.
Corollary 3.18. Let G be a locally bipartite graph which does not contain
![]() $H_{0}$
. If either
$H_{0}$
. If either
![]() $\delta(G) > 7/13 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, or
$\delta(G) > 7/13 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, or
![]() $\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and G does not contain
$\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and G does not contain
![]() $T_{0}$
, then G does not contain a sparse pair which is the missing spoke of an odd wheel.
$T_{0}$
, then G does not contain a sparse pair which is the missing spoke of an odd wheel.
3.4 The proof of Theorem 3.3
Here we will prove Theorem 3.3 which we restate for convenience.
Theorem 3.3. Let G be a locally bipartite graph. If
![]() $\delta(G)>8/15\cdot|G|$
, then G is either 3-colourable or contains
$\delta(G)>8/15\cdot|G|$
, then G is either 3-colourable or contains
![]() $H_0$
or
$H_0$
or
![]() $T_0$
. If
$T_0$
. If
![]() $\delta(G)>7/13\cdot|G|$
, then G is either 3-colourable or contains
$\delta(G)>7/13\cdot|G|$
, then G is either 3-colourable or contains
![]() $H_0$
.
$H_0$
.
We start with a locally bipartite graph G which does not contain
![]() $H_{0}$
and satisfies either
$H_{0}$
and satisfies either
![]() $\delta(G) > 7/13 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, or
$\delta(G) > 7/13 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, or
![]() $\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and G does not contain
$\delta(G) > 8/15 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and G does not contain
![]() $T_{0}$
. We are required to show that G is 3-colourable. We may assume that G is edge-maximal: for any sparse pair u, v of G, the addition of uv to G introduces an odd wheel, a copy of
$T_{0}$
. We are required to show that G is 3-colourable. We may assume that G is edge-maximal: for any sparse pair u, v of G, the addition of uv to G introduces an odd wheel, a copy of
![]() $H_{0}$
or a copy of
$H_{0}$
or a copy of
![]() $T_{0}$
. By Theorem 3.4, the addition of uv to G introduces an odd wheel, a copy of
$T_{0}$
. By Theorem 3.4, the addition of uv to G introduces an odd wheel, a copy of
![]() $H_{2}$
(since G itself does not contain
$H_{2}$
(since G itself does not contain
![]() $H_{2}$
) or a copy of
$H_{2}$
) or a copy of
![]() $T_{0}$
.
$T_{0}$
.
Firstly, if the addition of uv introduces an odd wheel, then, by Corollary 3.18, uv must be a rim of that wheel – this case is depicted in Figure 5(a) below. Secondly, if the addition of uv introduces a copy of
![]() $H_{2}$
, then that copy of
$H_{2}$
, then that copy of
![]() $H_{2}$
less the edge uv must not contain
$H_{2}$
less the edge uv must not contain
![]() $H_{0}$
– this case is depicted in Figure 5(b) to (f) below. Finally, suppose the addition of uv introduces a copy of
$H_{0}$
– this case is depicted in Figure 5(b) to (f) below. Finally, suppose the addition of uv introduces a copy of
![]() $T_{0}$
(but not an odd wheel nor a copy of
$T_{0}$
(but not an odd wheel nor a copy of
![]() $H_{0}$
). Label this copy of
$H_{0}$
). Label this copy of
![]() $T_{0}$
in
$T_{0}$
in
![]() $G + uv$
as follows.
$G + uv$
as follows.

Note that
![]() $G + uv$
is locally bipartite and does not contain
$G + uv$
is locally bipartite and does not contain
![]() $H_{0}$
so, by Lemma 3.8, for any vertex x,
$H_{0}$
so, by Lemma 3.8, for any vertex x,
![]() $D_{x} = \mathopen{}\left\{y \colon \text{the pair } x, y \text{ is dense}\right\}\mathclose{}$
is an independent set. In
$D_{x} = \mathopen{}\left\{y \colon \text{the pair } x, y \text{ is dense}\right\}\mathclose{}$
is an independent set. In
![]() $G + uv$
,
$G + uv$
,
![]() $t \in D_{v_{1}}$
and t is adjacent to
$t \in D_{v_{1}}$
and t is adjacent to
![]() $u_{1}$
so the pair
$u_{1}$
so the pair
![]() $u_{1}, v_{1}$
is not dense. Also,
$u_{1}, v_{1}$
is not dense. Also,
![]() $u_{1}v_{1}$
is not an edge in
$u_{1}v_{1}$
is not an edge in
![]() $G + uv$
(else
$G + uv$
(else
![]() $G + uv$
contains a 7-wheel centred at
$G + uv$
contains a 7-wheel centred at
![]() $u_{1}$
), so the pair
$u_{1}$
), so the pair
![]() $u_{1}, v_{1}$
is sparse in
$u_{1}, v_{1}$
is sparse in
![]() $G + uv$
. Therefore,
$G + uv$
. Therefore,
![]() $u_{1}, v_{1}$
is a sparse pair in G. Now, by Corollary 3.18, G does not contain an odd wheel missing a sparse spoke so uv must either be one of the edges
$u_{1}, v_{1}$
is a sparse pair in G. Now, by Corollary 3.18, G does not contain an odd wheel missing a sparse spoke so uv must either be one of the edges
![]() $v_{i}v_{i + 1}$
or one of the edges
$v_{i}v_{i + 1}$
or one of the edges
![]() $u_{1}v_{i}$
. Similarly, uv must either be one of the edges
$u_{1}v_{i}$
. Similarly, uv must either be one of the edges
![]() $v_{i}v_{i + 1}$
or one of the edges
$v_{i}v_{i + 1}$
or one of the edges
![]() $u_{6}v_{i}$
. Thus, in fact, uv must be one of the edges
$u_{6}v_{i}$
. Thus, in fact, uv must be one of the edges
![]() $v_{i}v_{i + 1,}$
and by symmetry, we may take
$v_{i}v_{i + 1,}$
and by symmetry, we may take
![]() $i = 0, 1, 2, 3$
– this case is depicted in Figure 5(g) to (j) below.
$i = 0, 1, 2, 3$
– this case is depicted in Figure 5(g) to (j) below.
Thus, in G, any sparse pair u, v must appear in one of the configurations shown in Figure 5 (with the labels of u and v possibly swapped).
We will now consider a largest independent set in G: an independent set I of size
![]() $\alpha(G)$
. We will shortly show that all vertices are either in I or adjacent to all of I.
$\alpha(G)$
. We will shortly show that all vertices are either in I or adjacent to all of I.
By Lemma 3.6, for every
![]() $u \in I$
,
$u \in I$
,
![]() $I \subset D_{u} \cup \mathopen{}\left\{u\right\}\mathclose{}$
. We now show there is set equality.
$I \subset D_{u} \cup \mathopen{}\left\{u\right\}\mathclose{}$
. We now show there is set equality.
Proposition 3.19. For every
![]() $u \in I$
,
$u \in I$
,
![]() $I = D_{u} \cup \mathopen{}\left\{u\right\}\mathclose{}$
$I = D_{u} \cup \mathopen{}\left\{u\right\}\mathclose{}$
Proof. By Lemma 3.8 and the definition of dense,
![]() $D_{u} \cup \mathopen{}\left\{u\right\}\mathclose{}$
is an independent set. However, it contains the maximal independent set I, so must equal it.
$D_{u} \cup \mathopen{}\left\{u\right\}\mathclose{}$
is an independent set. However, it contains the maximal independent set I, so must equal it.
The following definition will be helpful.

Figure 5. Configurations in which a sparse pair u, v may appear (labels u and v possibly swapped).
Definition 3.20. (quasidense) A pair of vertices u, v is quasidense if there is a sequence of vertices
![]() $u = d_{1}, d_{2}, \dotsc, d_{k}, d_{k + 1} = v$
such that all pairs
$u = d_{1}, d_{2}, \dotsc, d_{k}, d_{k + 1} = v$
such that all pairs
![]() $d_{i}, d_{i + 1}$
are dense
$d_{i}, d_{i + 1}$
are dense
![]() $(i = 1, 2, \dotsc, k)$
.
$(i = 1, 2, \dotsc, k)$
.
Proposition 3.19 immediately implies that if the pair u, v is quasidense and
![]() $u \in I$
, then
$u \in I$
, then
![]() $v \in I$
also.
$v \in I$
also.
Proposition 3.21. Every vertex of G is either in I or adjacent to all of I.
Proof. Fix a vertex
![]() $u \in I$
and let v be any other vertex which is not adjacent to u. It suffices to show that
$u \in I$
and let v be any other vertex which is not adjacent to u. It suffices to show that
![]() $v \in I$
. If the pair u, v is (quasi)dense, then
$v \in I$
. If the pair u, v is (quasi)dense, then
![]() $v \in I$
, so we may assume that u, v is sparse (and not quasidense). Thus, u, v appears in one of the configurations given in Figure 5 (with labels u and v possibly swapped). However, in each of Figure 5(a), (b), (e) and (g) to (j) the pair u, v is quasidense. Hence, we may assume that u, v appear in one of Figure 5(c), (d) and (f).
$v \in I$
, so we may assume that u, v is sparse (and not quasidense). Thus, u, v appears in one of the configurations given in Figure 5 (with labels u and v possibly swapped). However, in each of Figure 5(a), (b), (e) and (g) to (j) the pair u, v is quasidense. Hence, we may assume that u, v appear in one of Figure 5(c), (d) and (f).
We consider Figure 5(c) and (d) together. For ease, we label some more of the vertices as follows.

In both cases, the pair u
![]() $^{\prime}$
, w is dense, and so, by Lemma 3.8, the pair u
$^{\prime}$
, w is dense, and so, by Lemma 3.8, the pair u
![]() $^{\prime}$
, v
$^{\prime}$
, v
![]() $^{\prime}$
is not dense. However, u
$^{\prime}$
is not dense. However, u
![]() $^{\prime}$
v
$^{\prime}$
v
![]() $^{\prime}$
is not an edge, as the pair u, v is sparse, and so u
$^{\prime}$
is not an edge, as the pair u, v is sparse, and so u
![]() $^{\prime}$
, v
$^{\prime}$
, v
![]() $^{\prime}$
is a sparse pair. But then, uu
$^{\prime}$
is a sparse pair. But then, uu
![]() $^{\prime}$
vv
$^{\prime}$
vv
![]() $^{\prime}$
is an induced 4-cycle in which both non-edges are sparse which contradicts Lemma 3.7.
$^{\prime}$
is an induced 4-cycle in which both non-edges are sparse which contradicts Lemma 3.7.
Finally, we consider Figure 5(f) which we label as follows. Let
![]() $X = \mathopen{}\left\{u, v, v', v_{1}, v_{2}, v_{3}, v_{4}\right\}\mathclose{}$
and give a weighting
$X = \mathopen{}\left\{u, v, v', v_{1}, v_{2}, v_{3}, v_{4}\right\}\mathclose{}$
and give a weighting
![]() $\omega$
to the vertices of X as shown.
$\omega$
to the vertices of X as shown.

The pair v, v
![]() $^{\prime}$
is dense, so, if u, v
$^{\prime}$
is dense, so, if u, v
![]() $^{\prime}$
is quasidense, then u, v is quasidense, a contradiction. Also, as G is
$^{\prime}$
is quasidense, then u, v is quasidense, a contradiction. Also, as G is
![]() $H_{0}$
-free, uv
$H_{0}$
-free, uv
![]() $^{\prime}$
is not an edge. Hence, the pair u, v
$^{\prime}$
is not an edge. Hence, the pair u, v
![]() $^{\prime}$
is sparse and not quasidense. Now v, v
$^{\prime}$
is sparse and not quasidense. Now v, v
![]() $^{\prime}$
is dense and so, by Lemma 3.8, the pair
$^{\prime}$
is dense and so, by Lemma 3.8, the pair
![]() $vv_{4}$
is not. But
$vv_{4}$
is not. But
![]() $vv_{4}$
is not an edge (else u, v is dense), so
$vv_{4}$
is not an edge (else u, v is dense), so
![]() $v, v_{4}$
is a sparse pair. Similarly,
$v, v_{4}$
is a sparse pair. Similarly,
![]() $v', v_{1}$
is a sparse pair. To summarise, the pairs u, v and u, v
$v', v_{1}$
is a sparse pair. To summarise, the pairs u, v and u, v
![]() $^{\prime}$
are sparse and not quasidense and the pairs
$^{\prime}$
are sparse and not quasidense and the pairs
![]() $v, v_{4}$
and
$v, v_{4}$
and
![]() $v', v_{1}$
are sparse. It follows that G[X] contains no more edges than shown.
$v', v_{1}$
are sparse. It follows that G[X] contains no more edges than shown.
If a vertex x has five neighbours in X, then it is adjacent to three consecutive vertices round the 7-cycle, so x is either adjacent to a triangle or to all of
![]() $u, v_{1}, v$
or to all of
$u, v_{1}, v$
or to all of
![]() $v', v_{4}, u$
. The first gives a
$v', v_{4}, u$
. The first gives a
![]() $K_{4}$
while the latter two contradict the pairs u, v and u, v
$K_{4}$
while the latter two contradict the pairs u, v and u, v
![]() $^{\prime}$
being sparse. Hence, all vertices have at most four neighbours in X.
$^{\prime}$
being sparse. Hence, all vertices have at most four neighbours in X.
For each vertex x in G, let f(x) be the total weight of the neighbours of x in X. Now
so some vertex x has
![]() $f(x) \geqslant 9$
. All vertices of X have f value at most eight, so
$f(x) \geqslant 9$
. All vertices of X have f value at most eight, so
![]() $x \not \in X$
. As x has at most four neighbours in X, either x is adjacent to both
$x \not \in X$
. As x has at most four neighbours in X, either x is adjacent to both
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{4}$
or x is adjacent to exactly one of
$v_{4}$
or x is adjacent to exactly one of
![]() $v_{1}$
,
$v_{1}$
,
![]() $v_{4}$
and both of
$v_{4}$
and both of
![]() $v_{2}$
,
$v_{2}$
,
![]() $v_{3}$
.
$v_{3}$
.
First suppose that x is adjacent to both
![]() $v_{1}$
and
$v_{1}$
and
![]() $v_{4}$
. As
$v_{4}$
. As
![]() $v, v_{4}$
is sparse, x is not adjacent to v. Similarly x is not adjacent to v
$v, v_{4}$
is sparse, x is not adjacent to v. Similarly x is not adjacent to v
![]() $^{\prime}$
. If x is adjacent to
$^{\prime}$
. If x is adjacent to
![]() $v_{2}$
, then x, v is dense (the edge
$v_{2}$
, then x, v is dense (the edge
![]() $v_{1}v_{2}$
). But also u, x is dense (the edge
$v_{1}v_{2}$
). But also u, x is dense (the edge
![]() $v_{1}v_{4}$
), so u, v is quasidense, a contradiction. Hence, x is not adjacent to
$v_{1}v_{4}$
), so u, v is quasidense, a contradiction. Hence, x is not adjacent to
![]() $v_{2}$
. Similarly x is not adjacent to
$v_{2}$
. Similarly x is not adjacent to
![]() $v_{3}$
, and so
$v_{3}$
, and so
![]() $f(x) = 8$
, a contradiction.
$f(x) = 8$
, a contradiction.
In the second case, we may assume, by symmetry, that x is adjacent to
![]() $v_{1}$
,
$v_{1}$
,
![]() $v_{2}$
,
$v_{2}$
,
![]() $v_{3}$
but not to
$v_{3}$
but not to
![]() $v_{4}$
. Then, x, v and x, v
$v_{4}$
. Then, x, v and x, v
![]() $^{\prime}$
are both dense pairs (the edge
$^{\prime}$
are both dense pairs (the edge
![]() $v_{2}v_{3}$
) so x is adjacent to neither v nor v
$v_{2}v_{3}$
) so x is adjacent to neither v nor v
![]() $^{\prime}$
. Finally, if x is adjacent to u, then
$^{\prime}$
. Finally, if x is adjacent to u, then
![]() $x, v_{4}$
is dense (the edge
$x, v_{4}$
is dense (the edge
![]() $uv_{1}$
). But then, the edge
$uv_{1}$
). But then, the edge
![]() $v_{4}v'$
is in
$v_{4}v'$
is in
![]() $D_{x}$
, contradicting Lemma 3.8. Hence,
$D_{x}$
, contradicting Lemma 3.8. Hence,
![]() $f(x) = 8$
, a contradiction.
$f(x) = 8$
, a contradiction.
Proof of Theorem 3.3. Let
![]() $u \in I$
. Proposition 3.21 gives
$u \in I$
. Proposition 3.21 gives
![]() $G[V(G) \setminus I] = G_{u}$
, so
$G[V(G) \setminus I] = G_{u}$
, so
![]() $G[V(G) \setminus I]$
is 2-colourable. Using a third colour for the independent set I gives a 3-colouring of G.
$G[V(G) \setminus I]$
is 2-colourable. Using a third colour for the independent set I gives a 3-colouring of G.
4 Locally b-partite graphs
In this section, we prove Theorem 1.3 in the case
![]() $a = 1$
, showing that, for
$a = 1$
, showing that, for
![]() $b \geqslant 3$
, any locally b-partite graph G with minimum degree greater than
$b \geqslant 3$
, any locally b-partite graph G with minimum degree greater than
![]() $(1 - 1/(b + 1/7)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
is
$(1 - 1/(b + 1/7)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
is
![]() $(b + 1)$
-colourable.
$(b + 1)$
-colourable.
The proof of this will be an induction upon b, with some ideas from the proof of Theorem 3.3 persisting. In this introduction to the section, we generalise some of our previous ideas to the locally b-partite case, and then, we give a sketch of the proof. We first generalise dense and sparse pairs.
Definition 4.1. (b-dense and b-sparse) A pair of non-adjacent, distinct vertices u, v in a graph G is b-dense if
![]() $G_{u, v}$
contains a b-clique and is b-sparse if
$G_{u, v}$
contains a b-clique and is b-sparse if
![]() $G_{u, v}$
does not contain a b-clique.
$G_{u, v}$
does not contain a b-clique.
This extends the notion of dense and sparse given in Definition 3.5 – the definitions given there are identical to those of 2-dense and 2-sparse. Note that any pair of distinct vertices is exactly one of ‘adjacent’, ‘b-dense’ or ‘b-sparse’. Another way to view being b-dense is being the missing edge of a
![]() $K_{b + 2}$
. Locally b-partite graphs are
$K_{b + 2}$
. Locally b-partite graphs are
![]() $K_{b + 2}$
-free so any pair of distinct vertices with a b-clique in their common neighbourhood must be non-adjacent and so b-dense. The following lemma will be helpful for lifting results from the locally bipartite case.
$K_{b + 2}$
-free so any pair of distinct vertices with a b-clique in their common neighbourhood must be non-adjacent and so b-dense. The following lemma will be helpful for lifting results from the locally bipartite case.
Lemma 4.2. (lifting) Let b, s be positive integers and
![]() $\gamma$
any real with
$\gamma$
any real with
![]() $b + \gamma > s$
. Let G be a graph with
$b + \gamma > s$
. Let G be a graph with
![]() $\delta(G) > (1 - 1/(b + \gamma)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. For any s-set
$\delta(G) > (1 - 1/(b + \gamma)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. For any s-set
![]() $X \subset V(G)$
, we have
$X \subset V(G)$
, we have
 \begin{align*}\mathopen{}\left\vert G_{X} \right\vert\mathclose{} & \geqslant s \delta(G) - (s - 1) \mathopen{}\left\vert G \right\vert\mathclose{} > \bigl(1 - \tfrac{s}{b + \gamma}\bigr) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}, \text{ and}\\[3pt]\delta(G_{X}) & > \big(1 - \tfrac{1}{b - s + \gamma}\big) \cdot \mathopen{}\left\vert G_{X} \right\vert\mathclose{}.\end{align*}
\begin{align*}\mathopen{}\left\vert G_{X} \right\vert\mathclose{} & \geqslant s \delta(G) - (s - 1) \mathopen{}\left\vert G \right\vert\mathclose{} > \bigl(1 - \tfrac{s}{b + \gamma}\bigr) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}, \text{ and}\\[3pt]\delta(G_{X}) & > \big(1 - \tfrac{1}{b - s + \gamma}\big) \cdot \mathopen{}\left\vert G_{X} \right\vert\mathclose{}.\end{align*}
Proof. Let
![]() $X = \mathopen{}\left\{x_{1}, \dotsc, x_{s}\right\}\mathclose{}$
. Note that for each
$X = \mathopen{}\left\{x_{1}, \dotsc, x_{s}\right\}\mathclose{}$
. Note that for each
![]() $v \in V(G)$
$v \in V(G)$
and summing over
![]() $v \in V(G)$
gives
$v \in V(G)$
gives
Note that
![]() $\delta(G_{X}) \geqslant \delta(G) - (\mathopen{}\left\vert G \right\vert\mathclose{} - \mathopen{}\left\vert G_{X} \right\vert\mathclose{}) = \mathopen{}\left\vert G_{X} \right\vert\mathclose{} - (\mathopen{}\left\vert G \right\vert\mathclose{} - \delta(G))$
so
$\delta(G_{X}) \geqslant \delta(G) - (\mathopen{}\left\vert G \right\vert\mathclose{} - \mathopen{}\left\vert G_{X} \right\vert\mathclose{}) = \mathopen{}\left\vert G_{X} \right\vert\mathclose{} - (\mathopen{}\left\vert G \right\vert\mathclose{} - \delta(G))$
so
 \begin{align*}\frac{\delta(G_{X})}{\mathopen{}\left\vert G_{X} \right\vert\mathclose{}} & \geqslant 1 - \frac{\mathopen{}\left\vert G \right\vert\mathclose{} - \delta(G)}{\mathopen{}\left\vert G \right\vert\mathclose{}} \cdot \frac{\mathopen{}\left\vert G \right\vert\mathclose{}}{\mathopen{}\left\vert G_{X} \right\vert\mathclose{}} > 1 - \biggl(1 - \frac{\delta(G)}{\mathopen{}\left\vert G \right\vert\mathclose{}}\biggr) \cdot \frac{1}{1 - s/(b + \gamma)} \\[3pt]& > 1 - \frac{1}{b + \gamma} \cdot \frac{1}{1 - s/(b + \gamma)} = 1 - \frac{1}{b + \gamma - s}. \end{align*}
\begin{align*}\frac{\delta(G_{X})}{\mathopen{}\left\vert G_{X} \right\vert\mathclose{}} & \geqslant 1 - \frac{\mathopen{}\left\vert G \right\vert\mathclose{} - \delta(G)}{\mathopen{}\left\vert G \right\vert\mathclose{}} \cdot \frac{\mathopen{}\left\vert G \right\vert\mathclose{}}{\mathopen{}\left\vert G_{X} \right\vert\mathclose{}} > 1 - \biggl(1 - \frac{\delta(G)}{\mathopen{}\left\vert G \right\vert\mathclose{}}\biggr) \cdot \frac{1}{1 - s/(b + \gamma)} \\[3pt]& > 1 - \frac{1}{b + \gamma} \cdot \frac{1}{1 - s/(b + \gamma)} = 1 - \frac{1}{b + \gamma - s}. \end{align*}
Remark 4.3. If, in Lemma 4.2, X is an s-clique and G is locally b-partite, then
![]() $G_{X}$
is
$G_{X}$
is
![]() $(b - s + 1)$
-colourable and for any
$(b - s + 1)$
-colourable and for any
![]() $u, v \in G_{X}$
, if the pair u, v is b-sparse in G, then u, v is
$u, v \in G_{X}$
, if the pair u, v is b-sparse in G, then u, v is
![]() $(b - s)$
-sparse in
$(b - s)$
-sparse in
![]() $G_{X}$
. (The former can be seen by taking a vertex
$G_{X}$
. (The former can be seen by taking a vertex
![]() $x \in X$
and noting that
$x \in X$
and noting that
![]() $G_{x}$
is b-colourable and contains the
$G_{x}$
is b-colourable and contains the
![]() $(s - 1)$
-clique
$(s - 1)$
-clique
![]() $X - \{x\}$
joined to
$X - \{x\}$
joined to
![]() $G_{X}$
; the latter by noting that if vertices
$G_{X}$
; the latter by noting that if vertices
![]() $u, v \in G_{X}$
form a
$u, v \in G_{X}$
form a
![]() $(b - s)$
-dense pair in
$(b - s)$
-dense pair in
![]() $G_{X}$
, then they form a b-dense pair in G.)
$G_{X}$
, then they form a b-dense pair in G.)
The next lemma extends Lemma 3.8 and partly explains why the situation for locally b-partite is simpler for
![]() $b \geqslant 3$
than for
$b \geqslant 3$
than for
![]() $b = 2$
. Lemma 3.8 said that in any locally bipartite
$b = 2$
. Lemma 3.8 said that in any locally bipartite
![]() $H_{0}$
-free graph, the set of vertices which form a dense pair with a fixed vertex is independent. Here, in place of
$H_{0}$
-free graph, the set of vertices which form a dense pair with a fixed vertex is independent. Here, in place of
![]() $H_{0}$
-free, we give a minimum degree condition which guarantees this – for
$H_{0}$
-free, we give a minimum degree condition which guarantees this – for
![]() $b \geqslant 3$
this minimum degree condition falls below the chromatic threshold so is, for our purposes, automatic. When
$b \geqslant 3$
this minimum degree condition falls below the chromatic threshold so is, for our purposes, automatic. When
![]() $b = 2$
, this minimum degree condition is 4/7, which corresponds to
$b = 2$
, this minimum degree condition is 4/7, which corresponds to
![]() $\overline{C}_{7}$
.
$\overline{C}_{7}$
.
Lemma 4.4. Let
![]() $b \geqslant 2$
be an integer and G be a locally b-partite graph with
$b \geqslant 2$
be an integer and G be a locally b-partite graph with
![]() $\delta(G) > 2b/(2b + 3) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. For each vertex v of G,
$\delta(G) > 2b/(2b + 3) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. For each vertex v of G,
is an independent set of vertices.
Proof. Suppose that in fact there are vertices v,
![]() $u_{1}$
and
$u_{1}$
and
![]() $u_{2}$
with both pairs
$u_{2}$
with both pairs
![]() $v, u_{1}$
and
$v, u_{1}$
and
![]() $v, u_{2}$
b-dense as well as
$v, u_{2}$
b-dense as well as
![]() $u_{1}$
adjacent to
$u_{1}$
adjacent to
![]() $u_{2}$
. Let
$u_{2}$
. Let
![]() $Q_{1}$
and
$Q_{1}$
and
![]() $Q_{2}$
be b-cliques in
$Q_{2}$
be b-cliques in
![]() $G_{v, u_{1}}$
and
$G_{v, u_{1}}$
and
![]() $G_{v, u_{2,}}$
respectively. Choose
$G_{v, u_{2,}}$
respectively. Choose
![]() $Q_{1}$
and
$Q_{1}$
and
![]() $Q_{2}$
so that
$Q_{2}$
so that
![]() $\ell = \mathopen{}\left\vert V(Q_{1}) \cap V(Q_{2}) \right\vert\mathclose{}$
is maximal.
$\ell = \mathopen{}\left\vert V(Q_{1}) \cap V(Q_{2}) \right\vert\mathclose{}$
is maximal.
Firstly if
![]() $\ell \geqslant 1$
, then fix
$\ell \geqslant 1$
, then fix
![]() $y \in V(Q_{1}) \cap V(Q_{2})$
. Now
$y \in V(Q_{1}) \cap V(Q_{2})$
. Now
![]() $G_{y}$
contains
$G_{y}$
contains

The pair
![]() $v, u_{1}$
is
$v, u_{1}$
is
![]() $(b - 1)$
-dense in
$(b - 1)$
-dense in
![]() $G_{y}$
so in any b-colouring of
$G_{y}$
so in any b-colouring of
![]() $G_{y}$
, v and
$G_{y}$
, v and
![]() $u_{1}$
are the same colour. Similarly in any b-colouring of
$u_{1}$
are the same colour. Similarly in any b-colouring of
![]() $G_{y}$
, v and
$G_{y}$
, v and
![]() $u_{2}$
are the same colour. In particular,
$u_{2}$
are the same colour. In particular,
![]() $G_{y}$
is not b-colourable which contradicts the local b-colourability of G.
$G_{y}$
is not b-colourable which contradicts the local b-colourability of G.
Hence,
![]() $\ell = 0$
. Let
$\ell = 0$
. Let
![]() $X = V(Q_{1}) \cup V(Q_{2}) \cup \mathopen{}\left\{v, u_{1}, u_{2}\right\}\mathclose{}$
which is a set of
$X = V(Q_{1}) \cup V(Q_{2}) \cup \mathopen{}\left\{v, u_{1}, u_{2}\right\}\mathclose{}$
which is a set of
![]() $2b + 3$
vertices. As
$2b + 3$
vertices. As
![]() $\delta(G) > 2b/(2b + 3) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, some vertex has at least
$\delta(G) > 2b/(2b + 3) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, some vertex has at least
![]() $2b + 1$
neighbours in X – call this vertex x. As
$2b + 1$
neighbours in X – call this vertex x. As
![]() $G_{x}$
is
$G_{x}$
is
![]() $K_{b + 1}$
-free, x has a non-neighbour
$K_{b + 1}$
-free, x has a non-neighbour
![]() $x_{1} \in V(Q_{1}) \cup \mathopen{}\left\{u_{1}\right\}\mathclose{}$
and a non-neighbour
$x_{1} \in V(Q_{1}) \cup \mathopen{}\left\{u_{1}\right\}\mathclose{}$
and a non-neighbour
![]() $x_{2} \in V(Q_{2}) \cup \mathopen{}\left\{u_{2}\right\}\mathclose{}$
. These must be the only non-neighbours of x in X. In particular, x is adjacent to v and so, as
$x_{2} \in V(Q_{2}) \cup \mathopen{}\left\{u_{2}\right\}\mathclose{}$
. These must be the only non-neighbours of x in X. In particular, x is adjacent to v and so, as
![]() $G_{x}$
is
$G_{x}$
is
![]() $K_{b + 1}$
-free,
$K_{b + 1}$
-free,
![]() $x_{1}$
must be in
$x_{1}$
must be in
![]() $V(Q_{1})$
and
$V(Q_{1})$
and
![]() $x_{2}$
must be in
$x_{2}$
must be in
![]() $V(Q_{2})$
. In particular,
$V(Q_{2})$
. In particular,
![]() ${Q^{\prime}_{1}} = Q_{1} - \mathopen{}\left\{x_{1}\right\}\mathclose{} + \mathopen{}\left\{x\right\}\mathclose{}$
is a b-clique in
${Q^{\prime}_{1}} = Q_{1} - \mathopen{}\left\{x_{1}\right\}\mathclose{} + \mathopen{}\left\{x\right\}\mathclose{}$
is a b-clique in
![]() $G_{v, u_{1}}$
and
$G_{v, u_{1}}$
and
![]() ${Q^{\prime}_{2}} = Q_{2} - \mathopen{}\left\{x_{2}\right\}\mathclose{} + \mathopen{}\left\{x\right\}\mathclose{}$
is a b-clique in
${Q^{\prime}_{2}} = Q_{2} - \mathopen{}\left\{x_{2}\right\}\mathclose{} + \mathopen{}\left\{x\right\}\mathclose{}$
is a b-clique in
![]() $G_{v, u_{2}}$
. But
$G_{v, u_{2}}$
. But
![]() $\mathopen{}\left\vert V({Q^{\prime}_{1}}) \cap V({Q^{\prime}_{2}}) \right\vert\mathclose{} = 1$
which contradicts the maximality of
$\mathopen{}\left\vert V({Q^{\prime}_{1}}) \cap V({Q^{\prime}_{2}}) \right\vert\mathclose{} = 1$
which contradicts the maximality of
![]() $\ell$
.
$\ell$
.
Note that
for all
![]() $b \geqslant 3$
. We are only interested in locally b-partite graphs with
$b \geqslant 3$
. We are only interested in locally b-partite graphs with
![]() $\delta(G) > (1 - 1/b) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
(the chromatic threshold) and the conclusion of Lemma 4.4 holds for all such graphs.
$\delta(G) > (1 - 1/b) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
(the chromatic threshold) and the conclusion of Lemma 4.4 holds for all such graphs.
We are now ready to give a sketch of Theorem 1.3 for locally b-partite graphs. Let G be a locally b-partite graph (
![]() $b \geqslant 3$
) with
$b \geqslant 3$
) with
![]() $\delta(G) > (1 - 1/(b + 1/7)) \mathopen{}\left\vert G \right\vert\mathclose{}$
. We aim to show that G is
$\delta(G) > (1 - 1/(b + 1/7)) \mathopen{}\left\vert G \right\vert\mathclose{}$
. We aim to show that G is
![]() $(b + 1)$
-colourable. We may assume that G is edge-maximal: for any missing edge uv,
$(b + 1)$
-colourable. We may assume that G is edge-maximal: for any missing edge uv,
![]() $G' = G + uv$
is not locally b-partite. Using induction on b and the lifting lemma, we will show there is some
$G' = G + uv$
is not locally b-partite. Using induction on b and the lifting lemma, we will show there is some
![]() $(b - 2)$
-clique K with
$(b - 2)$
-clique K with
![]() ${G^{\prime}_{K}}$
not 3-colourable.
${G^{\prime}_{K}}$
not 3-colourable.
We will rule out the configurations where at least one of u, v is in K and so
![]() $u, v \not\in K$
. Since G is locally b-partite,
$u, v \not\in K$
. Since G is locally b-partite,
![]() $G_{K}$
is 3-colourable and also, using the lifting lemma, we will obtain
$G_{K}$
is 3-colourable and also, using the lifting lemma, we will obtain
![]() $\delta(G_{K}) > 8/15 \cdot \mathopen{}\left\vert G_{K} \right\vert\mathclose{}$
. As
$\delta(G_{K}) > 8/15 \cdot \mathopen{}\left\vert G_{K} \right\vert\mathclose{}$
. As
![]() $G_{K}$
is 3-colourable while
$G_{K}$
is 3-colourable while
![]() ${G^{\prime}_{K}}$
is not, we must have
${G^{\prime}_{K}}$
is not, we must have
![]() ${G^{\prime}_{K}} = G_{K} + uv$
. Further, by Theorem 3.3, the addition of uv to
${G^{\prime}_{K}} = G_{K} + uv$
. Further, by Theorem 3.3, the addition of uv to
![]() $G_{K}$
introduces an odd wheel, a copy of
$G_{K}$
introduces an odd wheel, a copy of
![]() $H_{2}$
or a copy of
$H_{2}$
or a copy of
![]() $T_{0}$
. We are then in a position to use Lemma 4.4 and finish in similar (although more involved) way to Section 3.4.
$T_{0}$
. We are then in a position to use Lemma 4.4 and finish in similar (although more involved) way to Section 3.4.
The ruling out of configurations is done in Section 4.1 while the rest of the proof is presented in Section 4.2.
4.1 Ruling out configurations
In this section, we will rule out various configurations from locally b-partite graphs in a similar vein to Section 3.3. From now on, we will use
![]() $C_{\text{odd}}$
to denote any odd cycle.
$C_{\text{odd}}$
to denote any odd cycle.
Proposition 4.5. Fix an integer
![]() $b \geqslant 3$
, let G be a locally b-partite graph with
$b \geqslant 3$
, let G be a locally b-partite graph with
![]() $\delta(G) > (1 - 1/(b + 1/7)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and let u, v be a b-sparse pair in G. Then
$\delta(G) > (1 - 1/(b + 1/7)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and let u, v be a b-sparse pair in G. Then
![]() $G + uv$
does not contain a
$G + uv$
does not contain a
![]() $K_{b - 1} + C_{\text{odd}}$
where at least one of u, v is in the
$K_{b - 1} + C_{\text{odd}}$
where at least one of u, v is in the
![]() $K_{b - 1}$
.
$K_{b - 1}$
.
Proof. We will prove this for
![]() $b = 3$
and then use the lifting lemma for larger b.
$b = 3$
and then use the lifting lemma for larger b.
For
![]() $b = 3$
, G is a locally tripartite graph with
$b = 3$
, G is a locally tripartite graph with
![]() $\delta(G) > 15/22 \cdot \mathopen{}\left\vert G \right\vert\mathclose{} > 2/3 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and u, v is a 3-sparse pair in G. Suppose the conclusion does not hold. Each neighbourhood of G is 3-colourable so does not contain an odd wheel. In particular, G does not contain
$\delta(G) > 15/22 \cdot \mathopen{}\left\vert G \right\vert\mathclose{} > 2/3 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and u, v is a 3-sparse pair in G. Suppose the conclusion does not hold. Each neighbourhood of G is 3-colourable so does not contain an odd wheel. In particular, G does not contain
![]() $K_{2} + C_{\text{odd}}$
, and so G contains one of the following two configurations (corresponding to whether only one of u, v is in the clique or they both are). In the left figure, x is adjacent to all vertices inside the ring, and in the right figure, u and v are adjacent to all vertices inside the ring. In the future, we will use rings in this way.
$K_{2} + C_{\text{odd}}$
, and so G contains one of the following two configurations (corresponding to whether only one of u, v is in the clique or they both are). In the left figure, x is adjacent to all vertices inside the ring, and in the right figure, u and v are adjacent to all vertices inside the ring. In the future, we will use rings in this way.

We deal with the left-hand configuration first. Odd wheels,
![]() $H_{0}$
and
$H_{0}$
and
![]() $T_{0}$
are not 3-colourable and so
$T_{0}$
are not 3-colourable and so
![]() $G_{x}$
is locally bipartite,
$G_{x}$
is locally bipartite,
![]() $H_{0}$
-free and
$H_{0}$
-free and
![]() $T_{0}$
-free. Applying Lemma 4.2 with
$T_{0}$
-free. Applying Lemma 4.2 with
![]() $X = \mathopen{}\left\{x\right\}\mathclose{}$
and
$X = \mathopen{}\left\{x\right\}\mathclose{}$
and
![]() $\gamma = 1/7$
gives
$\gamma = 1/7$
gives
![]() $\delta(G_{x}) > (1 - 1/(2 + 1/7)) \cdot \mathopen{}\left\vert G_{x} \right\vert\mathclose{} = 8/15 \cdot \mathopen{}\left\vert G_{x} \right\vert\mathclose{}$
so, by Corollary 3.18,
$\delta(G_{x}) > (1 - 1/(2 + 1/7)) \cdot \mathopen{}\left\vert G_{x} \right\vert\mathclose{} = 8/15 \cdot \mathopen{}\left\vert G_{x} \right\vert\mathclose{}$
so, by Corollary 3.18,
![]() $G_{x}$
does not contain a sparse pair which is the missing spoke of an odd wheel. In particular, the pair u, v is dense in
$G_{x}$
does not contain a sparse pair which is the missing spoke of an odd wheel. In particular, the pair u, v is dense in
![]() $G_{x}$
so must be 3-dense in G, a contradiction.
$G_{x}$
so must be 3-dense in G, a contradiction.
Now consider the right-hand configuration. We may assume that k is minimal. As the pair u, v is 3-sparse,
![]() $k > 1$
. Let
$k > 1$
. Let
![]() $X = \mathopen{}\left\{u, v, v_{0}, v_{1}, \dotsc, v_{2k}\right\}\mathclose{}$
. We consider indices modulo
$X = \mathopen{}\left\{u, v, v_{0}, v_{1}, \dotsc, v_{2k}\right\}\mathclose{}$
. We consider indices modulo
![]() $2k + 1$
.
$2k + 1$
.
First consider a vertex x adjacent to both u and v. We claim that x is adjacent to at most two of the
![]() $v_{i}$
so has at most four neighbours in X. For
$v_{i}$
so has at most four neighbours in X. For
![]() $r \not \in \mathopen{}\left\{0, \pm 2\right\}\mathclose{}$
, x cannot be adjacent to both
$r \not \in \mathopen{}\left\{0, \pm 2\right\}\mathclose{}$
, x cannot be adjacent to both
![]() $v_{i}$
and
$v_{i}$
and
![]() $v_{i + r}$
. Indeed if
$v_{i + r}$
. Indeed if
![]() $r = \pm 1$
, then
$r = \pm 1$
, then
![]() $xv_{i}v_{i + r}$
is a triangle in
$xv_{i}v_{i + r}$
is a triangle in
![]() $G_{u,v}$
while other r give a shorter odd cycle in
$G_{u,v}$
while other r give a shorter odd cycle in
![]() $G_{u,v}$
.
$G_{u,v}$
.
Now consider any other vertex x: this is not adjacent to at least one of u or v. If this is the only non-neighbour of x in X, then
![]() $G_{x}$
contains an odd-wheel, which is not 3-colourable. Thus, all vertices have at most
$G_{x}$
contains an odd-wheel, which is not 3-colourable. Thus, all vertices have at most
![]() $2k + 1$
neighbours in X. Hence,
$2k + 1$
neighbours in X. Hence,
 \begin{align*}(2k + 3) \delta(G) & \leqslant e(G, X) \leqslant 4 \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{} + (2k + 1)(\mathopen{}\left\vert G \right\vert\mathclose{} - \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{}) \\[3pt]& \leqslant (2k + 1) \mathopen{}\left\vert G \right\vert\mathclose{} - (2k - 3)(2 \delta(G) - \mathopen{}\left\vert G \right\vert\mathclose{}) = (4k -2) \mathopen{}\left\vert G \right\vert\mathclose{} - (4k - 6) \delta(G),\end{align*}
\begin{align*}(2k + 3) \delta(G) & \leqslant e(G, X) \leqslant 4 \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{} + (2k + 1)(\mathopen{}\left\vert G \right\vert\mathclose{} - \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{}) \\[3pt]& \leqslant (2k + 1) \mathopen{}\left\vert G \right\vert\mathclose{} - (2k - 3)(2 \delta(G) - \mathopen{}\left\vert G \right\vert\mathclose{}) = (4k -2) \mathopen{}\left\vert G \right\vert\mathclose{} - (4k - 6) \delta(G),\end{align*}
which contradicts
![]() $\delta(G) > 2/3 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
.
$\delta(G) > 2/3 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
.
Suppose now that
![]() $b \geqslant 4$
and that
$b \geqslant 4$
and that
![]() $G + uv$
does contain a
$G + uv$
does contain a
![]() $K_{b - 1} + C_{\text{odd}}$
where at least one of u, v is in the
$K_{b - 1} + C_{\text{odd}}$
where at least one of u, v is in the
![]() $K_{b - 1}$
. The
$K_{b - 1}$
. The
![]() $(b - 1)$
-clique contains a
$(b - 1)$
-clique contains a
![]() $(b - 3)$
-clique, L, with
$(b - 3)$
-clique, L, with
![]() $u, v \not \in L$
. Thus L is a
$u, v \not \in L$
. Thus L is a
![]() $(b - 3)$
-clique in G.
$(b - 3)$
-clique in G.
Now
![]() $G_{L}$
is a 4-colourable (so locally tripartite) graph in which u, v is 3-sparse (by Remark 4.3). Applying Lemma 4.2 with
$G_{L}$
is a 4-colourable (so locally tripartite) graph in which u, v is 3-sparse (by Remark 4.3). Applying Lemma 4.2 with
![]() $X = L$
,
$X = L$
,
![]() $\gamma = 1/7$
gives
$\gamma = 1/7$
gives
![]() $\delta(G_{L}) > (1 - 1/(b - (b - 3) + 1/7)) \cdot \mathopen{}\left\vert G_{L} \right\vert\mathclose{} = 15/22 \cdot \mathopen{}\left\vert G_{L} \right\vert\mathclose{}$
. Finally,
$\delta(G_{L}) > (1 - 1/(b - (b - 3) + 1/7)) \cdot \mathopen{}\left\vert G_{L} \right\vert\mathclose{} = 15/22 \cdot \mathopen{}\left\vert G_{L} \right\vert\mathclose{}$
. Finally,
![]() $G_{L} + uv$
contains a
$G_{L} + uv$
contains a
![]() $K_{2} + C_{\text{odd}}$
where at least one of u, v is in the 2-clique. This contradicts the result for
$K_{2} + C_{\text{odd}}$
where at least one of u, v is in the 2-clique. This contradicts the result for
![]() $b = 3$
.
$b = 3$
.
Proposition 4.6. Fix an integer
![]() $b \geqslant 3$
, let G be a locally b-partite graph with
$b \geqslant 3$
, let G be a locally b-partite graph with
![]() $\delta(G) > (1 - 1/(b + 1/7)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and let u, v be a b-sparse pair in G. Then,
$\delta(G) > (1 - 1/(b + 1/7)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and let u, v be a b-sparse pair in G. Then,
![]() $G + uv$
does not contain a
$G + uv$
does not contain a
![]() $K_{b - 2} + H_{0}$
where at least one of u, v is in the
$K_{b - 2} + H_{0}$
where at least one of u, v is in the
![]() $K_{b - 2}$
.
$K_{b - 2}$
.
Proof. We split into two cases depending upon whether only one of u, v is in the
![]() $(b - 2)$
-clique or both are. In each case, we will prove the result for small b and then use the lifting lemma for larger b.
$(b - 2)$
-clique or both are. In each case, we will prove the result for small b and then use the lifting lemma for larger b.
Suppose only one of u, v is in the
![]() $(b - 2)$
-clique. We first prove the result for
$(b - 2)$
-clique. We first prove the result for
![]() $b = 3$
: G is locally tripartite, the pair u, v is 3-sparse, and
$b = 3$
: G is locally tripartite, the pair u, v is 3-sparse, and
![]() $\delta(G) > 15/22 \cdot \mathopen{}\left\vert G \right\vert\mathclose{} > 2/3 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. Suppose the conclusion does not hold. Since G does not contain
$\delta(G) > 15/22 \cdot \mathopen{}\left\vert G \right\vert\mathclose{} > 2/3 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. Suppose the conclusion does not hold. Since G does not contain
![]() $K_{1} + H_{0}$
, G contains the configuration shown in Figure 6(a) where u is adjacent to all of the copy of
$K_{1} + H_{0}$
, G contains the configuration shown in Figure 6(a) where u is adjacent to all of the copy of
![]() $H_{0}$
except for one vertex (v) to which is it 3-sparse.
$H_{0}$
except for one vertex (v) to which is it 3-sparse.

Figure 6. Configurations in Proposition 4.6.
Let X be the vertex set of the
![]() $H_{0}$
. First, consider a vertex x adjacent to u: x cannot be adjacent to a triangle or 5-cycle in G[X] otherwise
$H_{0}$
. First, consider a vertex x adjacent to u: x cannot be adjacent to a triangle or 5-cycle in G[X] otherwise
![]() $G + uv$
contains a 2-clique ux joined to an odd cycle which contradicts Proposition 4.5. In particular, any neighbour of u has at most four neighbours in X.
$G + uv$
contains a 2-clique ux joined to an odd cycle which contradicts Proposition 4.5. In particular, any neighbour of u has at most four neighbours in X.
Consider any vertex x:
![]() $\chi(G[X]) = 4$
so x has at most six neighbours in X. Hence,
$\chi(G[X]) = 4$
so x has at most six neighbours in X. Hence,
which contradicts
![]() $\delta(G) > 15/22 \cdot \mathopen{}\left\vert G \right\vert\mathclose{} > 2/3 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
.
$\delta(G) > 15/22 \cdot \mathopen{}\left\vert G \right\vert\mathclose{} > 2/3 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
.
Now let
![]() $b \geqslant 4$
and suppose
$b \geqslant 4$
and suppose
![]() $G + uv$
does contain a
$G + uv$
does contain a
![]() $K_{b - 2} + H_{0}$
where exactly one of u, v (say u) is in the
$K_{b - 2} + H_{0}$
where exactly one of u, v (say u) is in the
![]() $(b - 2)$
-clique. Graph G is locally b-partite so does not contain
$(b - 2)$
-clique. Graph G is locally b-partite so does not contain
![]() $K_{b - 2} + H_{0}$
, so v is in the copy of
$K_{b - 2} + H_{0}$
, so v is in the copy of
![]() $H_{0}$
. Let L be the
$H_{0}$
. Let L be the
![]() $(b - 2)$
-clique without u: L is a
$(b - 2)$
-clique without u: L is a
![]() $(b - 3)$
-clique in G and so
$(b - 3)$
-clique in G and so
![]() $G_{L}$
is 4-colourable and so locally tripartite. Also, by Lemma 4.2,
$G_{L}$
is 4-colourable and so locally tripartite. Also, by Lemma 4.2,
![]() $\delta(G_{L}) > 15/22 \cdot \mathopen{}\left\vert G_{L} \right\vert\mathclose{}$
and, by Remark 4.3, u, v is a 3-sparse pair in
$\delta(G_{L}) > 15/22 \cdot \mathopen{}\left\vert G_{L} \right\vert\mathclose{}$
and, by Remark 4.3, u, v is a 3-sparse pair in
![]() $G_{L}$
. Finally,
$G_{L}$
. Finally,
![]() $G_{L} + uv$
contains
$G_{L} + uv$
contains
![]() $u + H_{0}$
, which contradicts the result we just proved for
$u + H_{0}$
, which contradicts the result we just proved for
![]() $b = 3$
.
$b = 3$
.
Now consider the second case, where both u and v are in the
![]() $(b - 2)$
-clique: this means that
$(b - 2)$
-clique: this means that
![]() $b \geqslant 4$
. We first prove the result for
$b \geqslant 4$
. We first prove the result for
![]() $b = 4$
: G is locally 4-partite, the pair u, v is 4-sparse, and
$b = 4$
: G is locally 4-partite, the pair u, v is 4-sparse, and
![]() $\delta(G) > 22/29 \cdot \mathopen{}\left\vert G \right\vert\mathclose{} > 3/4 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. If the result is false, then G contains the configuration shown in Figure 6(b).
$\delta(G) > 22/29 \cdot \mathopen{}\left\vert G \right\vert\mathclose{} > 3/4 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. If the result is false, then G contains the configuration shown in Figure 6(b).
Let
![]() $X = V(H_{0}) \cup \mathopen{}\left\{u\right\}\mathclose{}$
– a set of eight vertices. First, consider a vertex x adjacent to both u and v: x cannot be adjacent to a triangle or 5-cycle in
$X = V(H_{0}) \cup \mathopen{}\left\{u\right\}\mathclose{}$
– a set of eight vertices. First, consider a vertex x adjacent to both u and v: x cannot be adjacent to a triangle or 5-cycle in
![]() $V(H_{0})$
as this would contradict Proposition 4.5. Hence, x has at most four neighbours in
$V(H_{0})$
as this would contradict Proposition 4.5. Hence, x has at most four neighbours in
![]() $V(H_{0})$
and so at most five in X.
$V(H_{0})$
and so at most five in X.
Since G[X] is not 4-colourable, all vertices have at most seven neighbours in X. Hence,
 \begin{align*}8 \delta(G) & \leqslant 5 \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{} + 7(\mathopen{}\left\vert G \right\vert\mathclose{} - \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{}) \\[3pt]& \leqslant 7 \mathopen{}\left\vert G \right\vert\mathclose{} - 2(2 \delta(G) - \mathopen{}\left\vert G \right\vert\mathclose{}) = 9 \mathopen{}\left\vert G \right\vert\mathclose{} - 4 \delta(G),\end{align*}
\begin{align*}8 \delta(G) & \leqslant 5 \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{} + 7(\mathopen{}\left\vert G \right\vert\mathclose{} - \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{}) \\[3pt]& \leqslant 7 \mathopen{}\left\vert G \right\vert\mathclose{} - 2(2 \delta(G) - \mathopen{}\left\vert G \right\vert\mathclose{}) = 9 \mathopen{}\left\vert G \right\vert\mathclose{} - 4 \delta(G),\end{align*}
which contradicts
![]() $\delta(G) > 22/29 \cdot \mathopen{}\left\vert G \right\vert\mathclose{} > 3/4 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
.
$\delta(G) > 22/29 \cdot \mathopen{}\left\vert G \right\vert\mathclose{} > 3/4 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
.
Finally, suppose
![]() $b \geqslant 5$
and
$b \geqslant 5$
and
![]() $G + uv$
does contain a
$G + uv$
does contain a
![]() $K_{b - 2} + H_{0}$
where both of u, v are in the
$K_{b - 2} + H_{0}$
where both of u, v are in the
![]() $(b - 2)$
-clique. Let L be the
$(b - 2)$
-clique. Let L be the
![]() $(b - 2)$
-clique without u, v: L is a
$(b - 2)$
-clique without u, v: L is a
![]() $(b - 4)$
-clique in G so, by Remark 4.3,
$(b - 4)$
-clique in G so, by Remark 4.3,
![]() $G_{L}$
is 5-colourable and so locally 4-partite. Also, by Lemma 4.2,
$G_{L}$
is 5-colourable and so locally 4-partite. Also, by Lemma 4.2,
![]() $\delta(G_{L}) > 22/29 \cdot \mathopen{}\left\vert G_{L} \right\vert\mathclose{}$
and u, v is a 4-sparse pair in
$\delta(G_{L}) > 22/29 \cdot \mathopen{}\left\vert G_{L} \right\vert\mathclose{}$
and u, v is a 4-sparse pair in
![]() $G_{L}$
. Finally,
$G_{L}$
. Finally,
![]() $G_{L} + uv$
contains
$G_{L} + uv$
contains
![]() $uv + H_{0}$
, which contradicts the result we obtained for
$uv + H_{0}$
, which contradicts the result we obtained for
![]() $b = 4$
.
$b = 4$
.
Proposition 4.7. Fix an integer
![]() $b \geqslant 3$
, let G be a locally b-partite graph with
$b \geqslant 3$
, let G be a locally b-partite graph with
![]() $\delta(G) > (1 - 1/(b + 1/7)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and let u,v be a b-sparse pair in G. Then
$\delta(G) > (1 - 1/(b + 1/7)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
and let u,v be a b-sparse pair in G. Then
![]() $G + uv$
does not contain a
$G + uv$
does not contain a
![]() $K_{b - 2} + T_{0}$
where at least one of u, v is in the
$K_{b - 2} + T_{0}$
where at least one of u, v is in the
![]() $(b - 2)$
-clique.
$(b - 2)$
-clique.
Proof. Again we split into two cases depending upon whether only one of u, v is in the
![]() $(b - 2)$
-clique or both are, and in each case, we will prove the result for small b and then use the lifting lemma for larger b.
$(b - 2)$
-clique or both are, and in each case, we will prove the result for small b and then use the lifting lemma for larger b.
Suppose only one of u, v is in the
![]() $(b - 2)$
-clique. We first prove the result for
$(b - 2)$
-clique. We first prove the result for
![]() $b = 3$
: G is locally tripartite, the pair u, v is 3-sparse, and
$b = 3$
: G is locally tripartite, the pair u, v is 3-sparse, and
![]() $\delta(G) > 15/22 \cdot \mathopen{}\left\vert G \right\vert\mathclose{} > 2/3 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. Suppose the conclusion does not hold. Since G does not contain
$\delta(G) > 15/22 \cdot \mathopen{}\left\vert G \right\vert\mathclose{} > 2/3 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. Suppose the conclusion does not hold. Since G does not contain
![]() $K_{1} + T_{0}$
, G contains the configuration shown in Figure 7(a) (labels have been added for convenience) where u is adjacent to all of the copy of
$K_{1} + T_{0}$
, G contains the configuration shown in Figure 7(a) (labels have been added for convenience) where u is adjacent to all of the copy of
![]() $T_{0}$
except for one vertex (v) to which it is 3-sparse.
$T_{0}$
except for one vertex (v) to which it is 3-sparse.

Figure 7. Configurations in Proposition 4.7.
We first show that at least one of the pairs
![]() $u_{1}, v_{1}$
and
$u_{1}, v_{1}$
and
![]() $u_{6}, v_{6}$
is 3-sparse. Neither of these is an edge as otherwise
$u_{6}, v_{6}$
is 3-sparse. Neither of these is an edge as otherwise
![]() $G + uv$
contains u joined to a 7-wheel which contradicts Proposition 4.5. If
$G + uv$
contains u joined to a 7-wheel which contradicts Proposition 4.5. If
![]() $v \not \in \mathopen{}\left\{u_{1}, u_{6}, v_{3}, v_{4}\right\}\mathclose{}$
, then
$v \not \in \mathopen{}\left\{u_{1}, u_{6}, v_{3}, v_{4}\right\}\mathclose{}$
, then
![]() $u_{1}, u_{6}$
is 3-dense (triangle
$u_{1}, u_{6}$
is 3-dense (triangle
![]() $uv_{3}v_{4}$
) and so
$uv_{3}v_{4}$
) and so
![]() $u_{1}, v_{1}$
is 3-sparse, by Lemma 4.4. On the other hand, suppose
$u_{1}, v_{1}$
is 3-sparse, by Lemma 4.4. On the other hand, suppose
![]() $v \in \mathopen{}\left\{u_{1}, u_{6}, v_{3}, v_{4}\right\}\mathclose{}$
– by symmetry we may assume
$v \in \mathopen{}\left\{u_{1}, u_{6}, v_{3}, v_{4}\right\}\mathclose{}$
– by symmetry we may assume
![]() $v \neq u_{6}$
. Then,
$v \neq u_{6}$
. Then,
![]() $v_{1}, t$
is 3-dense (triangle
$v_{1}, t$
is 3-dense (triangle
![]() $uv_{0}u_{6}$
) and so
$uv_{0}u_{6}$
) and so
![]() $u_{1}, v_{1}$
is 3-sparse, by Lemma 4.4. From now on, we will assume that the pair
$u_{1}, v_{1}$
is 3-sparse, by Lemma 4.4. From now on, we will assume that the pair
![]() $u_{1}, v_{1}$
is 3-sparse in G.
$u_{1}, v_{1}$
is 3-sparse in G.
Let
![]() $G' = G + uv$
– we work in G
$G' = G + uv$
– we work in G
![]() $^{\prime}$
. From Proposition 4.5,
$^{\prime}$
. From Proposition 4.5,
![]() ${G^{\prime}_{u}}$
contains no odd wheel, i.e. is locally bipartite, and from Proposition 4.6,
${G^{\prime}_{u}}$
contains no odd wheel, i.e. is locally bipartite, and from Proposition 4.6,
![]() ${G^{\prime}_{u}}$
is
${G^{\prime}_{u}}$
is
![]() $H_{0}$
-free. Now
$H_{0}$
-free. Now
![]() $u_{1}v_{1}$
is not an edge (else there is a 7-wheel in
$u_{1}v_{1}$
is not an edge (else there is a 7-wheel in
![]() ${G^{\prime}_{u}}$
) and the pair
${G^{\prime}_{u}}$
) and the pair
![]() $v_{1}, t$
is 2-dense in
$v_{1}, t$
is 2-dense in
![]() ${G^{\prime}_{u}}$
so
${G^{\prime}_{u}}$
so
![]() $u_{1}, v_{1}$
is 2-sparse in
$u_{1}, v_{1}$
is 2-sparse in
![]() ${G^{\prime}_{u}}$
, by Lemma 3.8. Note that
${G^{\prime}_{u}}$
, by Lemma 3.8. Note that
![]() $\delta(G') > 2/3 \cdot \mathopen{}\left\vert G' \right\vert\mathclose{}$
and so applying Lemma 4.2 with
$\delta(G') > 2/3 \cdot \mathopen{}\left\vert G' \right\vert\mathclose{}$
and so applying Lemma 4.2 with
![]() $b = 3$
,
$b = 3$
,
![]() $\gamma = 0$
,
$\gamma = 0$
,
![]() $s = 1$
and
$s = 1$
and
![]() $X = \mathopen{}\left\{u\right\}\mathclose{}$
gives
$X = \mathopen{}\left\{u\right\}\mathclose{}$
gives
Hence, we may apply Lemma 3.11 to show that
![]() $u_{1}v_{1}$
is not a missing spoke of a 5-wheel in
$u_{1}v_{1}$
is not a missing spoke of a 5-wheel in
![]() ${G^{\prime}_{u}}$
. Hence, by Lemma 3.12, any neighbour of
${G^{\prime}_{u}}$
. Hence, by Lemma 3.12, any neighbour of
![]() $u_{1}$
in
$u_{1}$
in
![]() ${G^{\prime}_{u}}$
is adjacent to at most two of the
${G^{\prime}_{u}}$
is adjacent to at most two of the
![]() $v_{i}$
. In particular, any common neighbour of u and
$v_{i}$
. In particular, any common neighbour of u and
![]() $u_{1}$
in G
$u_{1}$
in G
![]() $^{\prime}$
is adjacent to at most two of the
$^{\prime}$
is adjacent to at most two of the
![]() $v_{i}$
.
$v_{i}$
.
Let
![]() $X = \mathopen{}\left\{u,u_{1},v_{0},v_{1}, \dotsc, v_{6}\right\}\mathclose{}$
. What we have just shown is that any common neighbour of u and
$X = \mathopen{}\left\{u,u_{1},v_{0},v_{1}, \dotsc, v_{6}\right\}\mathclose{}$
. What we have just shown is that any common neighbour of u and
![]() $u_{1}$
in G
$u_{1}$
in G
![]() $^{\prime}$
has at most four neighbours in X. Consider a vertex x which is not adjacent to both u and
$^{\prime}$
has at most four neighbours in X. Consider a vertex x which is not adjacent to both u and
![]() $u_{1}$
: x cannot be adjacent to all of
$u_{1}$
: x cannot be adjacent to all of
![]() $X \setminus \mathopen{}\left\{u_{1}\right\}\mathclose{}$
otherwise
$X \setminus \mathopen{}\left\{u_{1}\right\}\mathclose{}$
otherwise
![]() ${G^{\prime}_{u, x}}$
contains a 7-cycle which contradicts Proposition 4.5. Also, x cannot be adjacent to all of
${G^{\prime}_{u, x}}$
contains a 7-cycle which contradicts Proposition 4.5. Also, x cannot be adjacent to all of
![]() $X \setminus \mathopen{}\left\{u\right\}\mathclose{}$
as otherwise
$X \setminus \mathopen{}\left\{u\right\}\mathclose{}$
as otherwise
![]() ${G^{\prime}_{x}} = G_{x}$
contains a 7-wheel missing the spoke
${G^{\prime}_{x}} = G_{x}$
contains a 7-wheel missing the spoke
![]() $u_{1}v_{1}$
which is 3-sparse in G. This again contradicts Proposition 4.5. Hence, any vertex has at most seven neighbours in X. Thus,
$u_{1}v_{1}$
which is 3-sparse in G. This again contradicts Proposition 4.5. Hence, any vertex has at most seven neighbours in X. Thus,
which contradicts
![]() $\delta(G) > 2/3 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
.
$\delta(G) > 2/3 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
.
Now let
![]() $b \geqslant 4$
and suppose
$b \geqslant 4$
and suppose
![]() $G + uv$
does contain a
$G + uv$
does contain a
![]() $K_{b - 2} + T_{0}$
where exactly one of u, v (say u) is in the
$K_{b - 2} + T_{0}$
where exactly one of u, v (say u) is in the
![]() $(b - 2)$
-clique. Graph G is locally b-partite so does not contain
$(b - 2)$
-clique. Graph G is locally b-partite so does not contain
![]() $K_{b - 2} + T_{0}$
so v is in the copy of
$K_{b - 2} + T_{0}$
so v is in the copy of
![]() $T_{0}$
. Let L be the
$T_{0}$
. Let L be the
![]() $(b - 2)$
-clique without u. We make use of Remark 4.3: L is a
$(b - 2)$
-clique without u. We make use of Remark 4.3: L is a
![]() $(b - 3)$
-clique in G and so
$(b - 3)$
-clique in G and so
![]() $G_{L}$
is 4-colourable and so locally tripartite. Also, by Lemma 4.2,
$G_{L}$
is 4-colourable and so locally tripartite. Also, by Lemma 4.2,
![]() $\delta(G_{L}) > 15/22 \cdot \mathopen{}\left\vert G_{L} \right\vert\mathclose{}$
and u, v is a 3-sparse pair in
$\delta(G_{L}) > 15/22 \cdot \mathopen{}\left\vert G_{L} \right\vert\mathclose{}$
and u, v is a 3-sparse pair in
![]() $G_{L}$
. Finally,
$G_{L}$
. Finally,
![]() $G_{L} + uv$
contains
$G_{L} + uv$
contains
![]() $u + T_{0}$
, which contradicts the result we just proved for
$u + T_{0}$
, which contradicts the result we just proved for
![]() $b = 3$
.
$b = 3$
.
Now consider the second case, where both u and v are in the
![]() $(b - 2)$
-clique: this means that
$(b - 2)$
-clique: this means that
![]() $b \geqslant 4$
. We first prove the result for
$b \geqslant 4$
. We first prove the result for
![]() $b = 4$
: G is locally 4-partite, the pair u, v is 4-sparse, and
$b = 4$
: G is locally 4-partite, the pair u, v is 4-sparse, and
![]() $\delta(G) > 22/29 \cdot \mathopen{}\left\vert G \right\vert\mathclose{} > 3/4 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. If the result is false, then G contains the configuration shown in Figure 7(b) (labels have been added for convenience).
$\delta(G) > 22/29 \cdot \mathopen{}\left\vert G \right\vert\mathclose{} > 3/4 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. If the result is false, then G contains the configuration shown in Figure 7(b) (labels have been added for convenience).
By Propositions 4.5 and 4.6,
![]() $G_{u, v}$
is locally bipartite and
$G_{u, v}$
is locally bipartite and
![]() $H_{0}$
-free. By Lemma 3.2,
$H_{0}$
-free. By Lemma 3.2,
![]() $\delta(G_{u, v}) > 1/2 \cdot \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{}$
. Since
$\delta(G_{u, v}) > 1/2 \cdot \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{}$
. Since
![]() $G_{u, v}$
does not contain an odd wheel,
$G_{u, v}$
does not contain an odd wheel,
![]() $u_{1}v_{1}$
is not an edge. Also,
$u_{1}v_{1}$
is not an edge. Also,
![]() $v_{1}, t$
is a 2-dense pair,
$v_{1}, t$
is a 2-dense pair,
![]() $tu_{1}$
is an edge and
$tu_{1}$
is an edge and
![]() $G_{u, v}$
is
$G_{u, v}$
is
![]() $H_{0}$
-free, so, by Lemma 3.8,
$H_{0}$
-free, so, by Lemma 3.8,
![]() $u_{1}, v_{1}$
is a 2-sparse pair in
$u_{1}, v_{1}$
is a 2-sparse pair in
![]() $G_{u, v}$
. Similarly,
$G_{u, v}$
. Similarly,
![]() $u_{6}, v_{6}$
is 2-sparse in
$u_{6}, v_{6}$
is 2-sparse in
![]() $G_{u, v}$
.
$G_{u, v}$
.
Now let
![]() $X = \mathopen{}\left\{u, u_{1}, u_{6}, v_{0}, \dotsc, v_{6}\right\}\mathclose{}$
(note that this does not contain t or v). Within
$X = \mathopen{}\left\{u, u_{1}, u_{6}, v_{0}, \dotsc, v_{6}\right\}\mathclose{}$
(note that this does not contain t or v). Within
![]() $G_{u, v}$
,
$G_{u, v}$
,
![]() $u_{1}$
together with the
$u_{1}$
together with the
![]() $v_{i}$
form a 7-wheel missing the spoke
$v_{i}$
form a 7-wheel missing the spoke
![]() $u_{1}v_{1}$
which is a sparse pair. Since
$u_{1}v_{1}$
which is a sparse pair. Since
![]() $G_{u,v}$
is locally bipartite with
$G_{u,v}$
is locally bipartite with
![]() $\delta(G_{u, v}) > 1/2 \cdot \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{}$
, Lemma 3.11 implies that
$\delta(G_{u, v}) > 1/2 \cdot \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{}$
, Lemma 3.11 implies that
![]() $G_{u, v}$
does not contain any 5-wheels missing a sparse spoke. Hence, by Lemma 3.12, any neighbour of
$G_{u, v}$
does not contain any 5-wheels missing a sparse spoke. Hence, by Lemma 3.12, any neighbour of
![]() $u_{1}$
in
$u_{1}$
in
![]() $G_{u, v}$
is adjacent to at most two of the
$G_{u, v}$
is adjacent to at most two of the
![]() $v_{i}$
. Thus, any neighbour of u, v,
$v_{i}$
. Thus, any neighbour of u, v,
![]() $u_{1}$
has at most five neighbours in X (two amongst
$u_{1}$
has at most five neighbours in X (two amongst
![]() $v_{i}$
together with possibly
$v_{i}$
together with possibly
![]() $u_{1}, u_{6}, u$
). Similarly, any neighbour of u, v,
$u_{1}, u_{6}, u$
). Similarly, any neighbour of u, v,
![]() $u_{6}$
has at most five neighbours in X. Next, consider a vertex x adjacent to both u, v but to neither
$u_{6}$
has at most five neighbours in X. Next, consider a vertex x adjacent to both u, v but to neither
![]() $u_{1}$
nor
$u_{1}$
nor
![]() $u_{6}$
. As
$u_{6}$
. As
![]() $G_{u,v}$
is locally bipartite, x is adjacent to at most six of the
$G_{u,v}$
is locally bipartite, x is adjacent to at most six of the
![]() $v_{i}$
so x has at most seven neighbours in X. Finally,
$v_{i}$
so x has at most seven neighbours in X. Finally,
![]() $\chi(G[X]) = 5$
so all vertices have at most nine neighbours in X. Hence,
$\chi(G[X]) = 5$
so all vertices have at most nine neighbours in X. Hence,
 \begin{align*}10 \delta(G) & \leqslant 5\mathopen{}\left\vert \Gamma(u, v, u_{1}) \cup \Gamma(u, v, u_{6}) \right\vert\mathclose{} + 7(\mathopen{}\left\vert G_{u, v} \right\vert\mathclose{} - \mathopen{}\left\vert \Gamma(u, v, u_{1}) \cup \Gamma(u, v, u_{6}) \right\vert\mathclose{}) + 9(\mathopen{}\left\vert G \right\vert\mathclose{} - \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{}) \\& = 9 \mathopen{}\left\vert G \right\vert\mathclose{} - 2 \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{} - 2 \mathopen{}\left\vert \Gamma(u, v, u_{1}) \cup \Gamma(u, v, u_{6}) \right\vert\mathclose{} \leqslant 9 \mathopen{}\left\vert G \right\vert\mathclose{} - 2 \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{} - 2 \mathopen{}\left\vert G_{u, v, u_{1}} \right\vert\mathclose{} \\& \leqslant 9 \mathopen{}\left\vert G \right\vert\mathclose{} - 2(2 \delta(G) - \mathopen{}\left\vert G \right\vert\mathclose{}) - 2(3 \delta(G) - 2 \mathopen{}\left\vert G \right\vert\mathclose{}) = 15 \mathopen{}\left\vert G \right\vert\mathclose{} - 10 \delta(G),\end{align*}
\begin{align*}10 \delta(G) & \leqslant 5\mathopen{}\left\vert \Gamma(u, v, u_{1}) \cup \Gamma(u, v, u_{6}) \right\vert\mathclose{} + 7(\mathopen{}\left\vert G_{u, v} \right\vert\mathclose{} - \mathopen{}\left\vert \Gamma(u, v, u_{1}) \cup \Gamma(u, v, u_{6}) \right\vert\mathclose{}) + 9(\mathopen{}\left\vert G \right\vert\mathclose{} - \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{}) \\& = 9 \mathopen{}\left\vert G \right\vert\mathclose{} - 2 \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{} - 2 \mathopen{}\left\vert \Gamma(u, v, u_{1}) \cup \Gamma(u, v, u_{6}) \right\vert\mathclose{} \leqslant 9 \mathopen{}\left\vert G \right\vert\mathclose{} - 2 \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{} - 2 \mathopen{}\left\vert G_{u, v, u_{1}} \right\vert\mathclose{} \\& \leqslant 9 \mathopen{}\left\vert G \right\vert\mathclose{} - 2(2 \delta(G) - \mathopen{}\left\vert G \right\vert\mathclose{}) - 2(3 \delta(G) - 2 \mathopen{}\left\vert G \right\vert\mathclose{}) = 15 \mathopen{}\left\vert G \right\vert\mathclose{} - 10 \delta(G),\end{align*}
which contradicts
![]() $\delta(G) > 3/4 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
.
$\delta(G) > 3/4 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
.
Now let
![]() $b \geqslant 5$
and suppose
$b \geqslant 5$
and suppose
![]() $G + uv$
does contain a
$G + uv$
does contain a
![]() $K_{b - 2} + T_{0}$
where both of u, v are in the
$K_{b - 2} + T_{0}$
where both of u, v are in the
![]() $(b - 2)$
-clique. Let L be the
$(b - 2)$
-clique. Let L be the
![]() $(b - 2)$
-clique without u, v: L is a
$(b - 2)$
-clique without u, v: L is a
![]() $(b - 4)$
-clique in G and so
$(b - 4)$
-clique in G and so
![]() $G_{L}$
is 5-colourable and so locally 4-partite. Also, by Lemma 4.2,
$G_{L}$
is 5-colourable and so locally 4-partite. Also, by Lemma 4.2,
![]() $\delta(G_{L}) > 22/29 \cdot \mathopen{}\left\vert G_{L} \right\vert\mathclose{}$
and, by Remark 4.3, the pair u, v is 4-sparse in
$\delta(G_{L}) > 22/29 \cdot \mathopen{}\left\vert G_{L} \right\vert\mathclose{}$
and, by Remark 4.3, the pair u, v is 4-sparse in
![]() $G_{L}$
. Finally,
$G_{L}$
. Finally,
![]() $G_{L} + uv$
contains
$G_{L} + uv$
contains
![]() $uv + T_{0}$
, which contradicts the result just proved for
$uv + T_{0}$
, which contradicts the result just proved for
![]() $b = 4$
.
$b = 4$
.
4.2 Finishing the proof
Here we will prove Theorem 1.3 for locally b-partite graphs.
Proof. Take an edge-maximal locally b-partite graph G with
![]() $\delta(G) > (1 - 1/(b + 1/7)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. We need to show that G is
$\delta(G) > (1 - 1/(b + 1/7)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. We need to show that G is
![]() $(b + 1)$
-colourable. We may assume by induction that the theorem holds for all b
$(b + 1)$
-colourable. We may assume by induction that the theorem holds for all b
![]() $^{\prime}$
with
$^{\prime}$
with
![]() $3 \leqslant b' < b$
(if there are any).
$3 \leqslant b' < b$
(if there are any).
We first show that for any b-sparse pair u, v of G,
![]() $G' = G + uv$
contains a
$G' = G + uv$
contains a
![]() $(b - 2)$
-clique K with
$(b - 2)$
-clique K with
![]() ${G^{\prime}_{K}}$
not 3-colourable. Indeed, for
${G^{\prime}_{K}}$
not 3-colourable. Indeed, for
![]() $b = 3$
, G
$b = 3$
, G
![]() $^{\prime}$
is not locally tripartite (by edge-maximality) so there is a vertex in G
$^{\prime}$
is not locally tripartite (by edge-maximality) so there is a vertex in G
![]() $^{\prime}$
whose neighbourhood is not 3-colourable. Take K to be this vertex. For
$^{\prime}$
whose neighbourhood is not 3-colourable. Take K to be this vertex. For
![]() $b > 3$
, G
$b > 3$
, G
![]() $^{\prime}$
is not locally b-partite so contains a vertex
$^{\prime}$
is not locally b-partite so contains a vertex
![]() $w_{1}$
with
$w_{1}$
with
![]() ${G^{\prime}_{w_{1}}}$
not b-colourable. Applying Lemma 4.2 with
${G^{\prime}_{w_{1}}}$
not b-colourable. Applying Lemma 4.2 with
![]() $X = \mathopen{}\left\{w_{1}\right\}\mathclose{}$
and
$X = \mathopen{}\left\{w_{1}\right\}\mathclose{}$
and
![]() $\gamma = 1/7$
gives
$\gamma = 1/7$
gives
By the induction hypothesis, if
![]() ${G^{\prime}_{w_{1}}}$
was locally
${G^{\prime}_{w_{1}}}$
was locally
![]() $(b - 1)$
-partite, then it would be b-colourable. In particular,
$(b - 1)$
-partite, then it would be b-colourable. In particular,
![]() ${G^{\prime}_{w_{1}}}$
is not locally
${G^{\prime}_{w_{1}}}$
is not locally
![]() $(b - 1)$
-partite and so there is a vertex
$(b - 1)$
-partite and so there is a vertex
![]() $w_{2}$
in
$w_{2}$
in
![]() ${G^{\prime}_{w_{1}}}$
with
${G^{\prime}_{w_{1}}}$
with
![]() ${G^{\prime}_{w_{1}, w_{2}}}$
not
${G^{\prime}_{w_{1}, w_{2}}}$
not
![]() $(b - 1)$
-colourable. Repeating this argument gives a
$(b - 1)$
-colourable. Repeating this argument gives a
![]() $(b - 2)$
-clique K with
$(b - 2)$
-clique K with
![]() ${G^{\prime}_{K}}$
not 3-colourable.
${G^{\prime}_{K}}$
not 3-colourable.
Now, applying Lemma 4.2 with
![]() $X = K$
and
$X = K$
and
![]() $\gamma = 1/7$
gives
$\gamma = 1/7$
gives
By Theorems 3.3 and 3.4,
![]() ${G^{\prime}_{K}}$
contains either an odd wheel, a copy of
${G^{\prime}_{K}}$
contains either an odd wheel, a copy of
![]() $H_{2}$
, or a copy of
$H_{2}$
, or a copy of
![]() $T_{0}$
. Hence, G
$T_{0}$
. Hence, G
![]() $^{\prime}$
contains either
$^{\prime}$
contains either
![]() $K_{b - 2} + W_{\text{odd}} = K_{b - 1} + C_{\text{odd}}$
,
$K_{b - 2} + W_{\text{odd}} = K_{b - 1} + C_{\text{odd}}$
,
![]() $K_{b - 2} + H_{2}$
or
$K_{b - 2} + H_{2}$
or
![]() $K_{b - 2} + T_{0}$
. Note that G cannot contain any of these so uv is a missing edge from one of these configurations. Propositions 4.5 to 4.7 mean that both u and v lie in the
$K_{b - 2} + T_{0}$
. Note that G cannot contain any of these so uv is a missing edge from one of these configurations. Propositions 4.5 to 4.7 mean that both u and v lie in the
![]() $C_{\text{odd}}$
, the
$C_{\text{odd}}$
, the
![]() $H_{2}$
or the
$H_{2}$
or the
![]() $T_{0}$
.
$T_{0}$
.
In particular,
![]() $u, v \not \in K$
so K is a
$u, v \not \in K$
so K is a
![]() $(b - 2)$
-clique in G and
$(b - 2)$
-clique in G and
![]() $V(G_{K}) = V({G^{\prime}_{K}})$
. We have the following facts.
$V(G_{K}) = V({G^{\prime}_{K}})$
. We have the following facts.
-
By Remark 4.3,
 $G_{K}$
is 3-colourable and so locally bipartite.
$G_{K}$
is 3-colourable and so locally bipartite. -
By Remark 4.3, u, v is a 2-sparse pair in
 $G_{K}$
.
$G_{K}$
. -
Applying Lemma 4.2 with
 $X = K$
and
$X = K$
and
 $\gamma = 1/7$
gives
$\gamma = 1/7$
gives
 $\delta(G_{K}) > 8/15 \cdot \mathopen{}\left\vert G_{K} \right\vert\mathclose{}$
.
$\delta(G_{K}) > 8/15 \cdot \mathopen{}\left\vert G_{K} \right\vert\mathclose{}$
. -
The graph
 $G_{K}$
contains no odd wheel,
$G_{K}$
contains no odd wheel,
 $H_{0}$
or
$H_{0}$
or
 $T_{0}$
(
$T_{0}$
(
 $G_{K}$
is 3-colourable) but the addition of uv introduces an odd wheel, a copy of
$G_{K}$
is 3-colourable) but the addition of uv introduces an odd wheel, a copy of
 $H_{2}$
, or a copy of
$H_{2}$
, or a copy of
 $T_{0}$
.
$T_{0}$
.
Using the argument at the start of Section 3.4, we deduce that, within
![]() $G_{K}$
, there must be one of the configurations appearing in Figure 5 (with labels u and v possibly swapped). Note in that proof we only used edge-maximality to show that uv was the missing edge of an odd wheel, a copy of
$G_{K}$
, there must be one of the configurations appearing in Figure 5 (with labels u and v possibly swapped). Note in that proof we only used edge-maximality to show that uv was the missing edge of an odd wheel, a copy of
![]() $H_{2}$
or a copy of
$H_{2}$
or a copy of
![]() $T_{0}$
(and so here we do not need
$T_{0}$
(and so here we do not need
![]() $G_{K}$
to be an edge-maximal locally bipartite graph).
$G_{K}$
to be an edge-maximal locally bipartite graph).
We now mimic the remainder of the proof of Theorem 3.3. Let I be a largest independent set in G:
![]() $\mathopen{}\left\vert I \right\vert\mathclose{} = \alpha(G)$
.
$\mathopen{}\left\vert I \right\vert\mathclose{} = \alpha(G)$
.
Proposition 4.8. For all distinct
![]() $u, v \in I$
, the pair u, v is b-dense and furthermore every
$u, v \in I$
, the pair u, v is b-dense and furthermore every
![]() $u \in I$
has
$u \in I$
has
![]() $I = D_{u} \cup \mathopen{}\left\{u\right\}\mathclose{}$
.
$I = D_{u} \cup \mathopen{}\left\{u\right\}\mathclose{}$
.
Proof. Fix distinct
![]() $u, v \in I$
. We will first show that
$u, v \in I$
. We will first show that
![]() $G_{u, v}$
is not
$G_{u, v}$
is not
![]() $(b - 1)$
-colourable. Note that
$(b - 1)$
-colourable. Note that
![]() $\Gamma(u), \Gamma(v) \subset V(G) \setminus I$
so
$\Gamma(u), \Gamma(v) \subset V(G) \setminus I$
so
![]() $\mathopen{}\left\vert \Gamma(u) \cup \Gamma(v) \right\vert\mathclose{} \leqslant \mathopen{}\left\vert G \right\vert\mathclose{} - \mathopen{}\left\vert I \right\vert\mathclose{}$
. Also
$\mathopen{}\left\vert \Gamma(u) \cup \Gamma(v) \right\vert\mathclose{} \leqslant \mathopen{}\left\vert G \right\vert\mathclose{} - \mathopen{}\left\vert I \right\vert\mathclose{}$
. Also
![]() $I \subset V(G) \setminus \Gamma(u)$
, so
$I \subset V(G) \setminus \Gamma(u)$
, so
![]() $\mathopen{}\left\vert I \right\vert\mathclose{} \leqslant \mathopen{}\left\vert G \right\vert\mathclose{} - d(u) \leqslant \mathopen{}\left\vert G \right\vert\mathclose{} - \delta(G)$
. Hence,
$\mathopen{}\left\vert I \right\vert\mathclose{} \leqslant \mathopen{}\left\vert G \right\vert\mathclose{} - d(u) \leqslant \mathopen{}\left\vert G \right\vert\mathclose{} - \delta(G)$
. Hence,
 \begin{align*}\mathopen{}\left\vert \Gamma(u, v) \right\vert\mathclose{} & = d(u) + d(v) - \mathopen{}\left\vert \Gamma(u) \cup \Gamma(v) \right\vert\mathclose{} \geqslant 2 \delta(G) + \mathopen{}\left\vert I \right\vert\mathclose{} - \mathopen{}\left\vert G \right\vert\mathclose{} \\& = b \delta(G) - (b - 1) \mathopen{}\left\vert G \right\vert\mathclose{} + (b - 2)(\mathopen{}\left\vert G \right\vert\mathclose{} - \delta(G)) + \mathopen{}\left\vert I \right\vert\mathclose{} \\& \geqslant b \delta(G) - (b - 1) \mathopen{}\left\vert G \right\vert\mathclose{} + (b - 1) \mathopen{}\left\vert I \right\vert\mathclose{} > (b - 1) \mathopen{}\left\vert I \right\vert\mathclose{},\end{align*}
\begin{align*}\mathopen{}\left\vert \Gamma(u, v) \right\vert\mathclose{} & = d(u) + d(v) - \mathopen{}\left\vert \Gamma(u) \cup \Gamma(v) \right\vert\mathclose{} \geqslant 2 \delta(G) + \mathopen{}\left\vert I \right\vert\mathclose{} - \mathopen{}\left\vert G \right\vert\mathclose{} \\& = b \delta(G) - (b - 1) \mathopen{}\left\vert G \right\vert\mathclose{} + (b - 2)(\mathopen{}\left\vert G \right\vert\mathclose{} - \delta(G)) + \mathopen{}\left\vert I \right\vert\mathclose{} \\& \geqslant b \delta(G) - (b - 1) \mathopen{}\left\vert G \right\vert\mathclose{} + (b - 1) \mathopen{}\left\vert I \right\vert\mathclose{} > (b - 1) \mathopen{}\left\vert I \right\vert\mathclose{},\end{align*}
where we used
![]() $\delta(G) > (1 - 1/b) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
in the final inequality. But I was a largest independent set in G so
$\delta(G) > (1 - 1/b) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
in the final inequality. But I was a largest independent set in G so
![]() $G_{u, v}$
is not
$G_{u, v}$
is not
![]() $(b - 1)$
-colourable.
$(b - 1)$
-colourable.
Now, we will show that u, v is b-dense. Suppose not and so they form a b-sparse pair. If
![]() $b = 3$
, then
$b = 3$
, then
![]() $G_{u, v}$
is not bipartite and so contains an odd cycle. This contradicts Proposition 4.5. For
$G_{u, v}$
is not bipartite and so contains an odd cycle. This contradicts Proposition 4.5. For
![]() $b \geqslant 4,$
we will find a
$b \geqslant 4,$
we will find a
![]() $(b - 4)$
-clique K in
$(b - 4)$
-clique K in
![]() $G_{u, v}$
with
$G_{u, v}$
with
![]() $G_{u, v, K}$
not 3-colourable. For
$G_{u, v, K}$
not 3-colourable. For
![]() $b = 4$
, we take
$b = 4$
, we take
![]() $K = \varnothing$
and this suffices. For larger b, we note that, by Lemma 4.2,
$K = \varnothing$
and this suffices. For larger b, we note that, by Lemma 4.2,
![]() $\delta(G_{u, v}) > (1 - 1/(b - 2 + 1/7)) \cdot \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{}$
. By the induction hypothesis, if
$\delta(G_{u, v}) > (1 - 1/(b - 2 + 1/7)) \cdot \mathopen{}\left\vert G_{u, v} \right\vert\mathclose{}$
. By the induction hypothesis, if
![]() $G_{u, v}$
were locally
$G_{u, v}$
were locally
![]() $(b - 2)$
-partite, then
$(b - 2)$
-partite, then
![]() $G_{u, v}$
would be
$G_{u, v}$
would be
![]() $(b - 1)$
-colourable, which it is not. Thus, there is
$(b - 1)$
-colourable, which it is not. Thus, there is
![]() $w_{1} \in G_{u, v}$
with
$w_{1} \in G_{u, v}$
with
![]() $G_{u, v, w_{1}}$
not
$G_{u, v, w_{1}}$
not
![]() $(b - 2)$
-colourable. Repeating this argument we obtain a
$(b - 2)$
-colourable. Repeating this argument we obtain a
![]() $(b - 4)$
-clique K with
$(b - 4)$
-clique K with
![]() $G_{u, v, K}$
not 3-colourable. Applying Lemma 4.2 with
$G_{u, v, K}$
not 3-colourable. Applying Lemma 4.2 with
![]() $X = \mathopen{}\left\{u, v\right\}\mathclose{} \cup K$
and
$X = \mathopen{}\left\{u, v\right\}\mathclose{} \cup K$
and
![]() $\gamma = 1/7$
gives
$\gamma = 1/7$
gives
Then, Theorem 3.3 gives that
![]() $G_{u, v, K}$
either contains an odd wheel, a copy of
$G_{u, v, K}$
either contains an odd wheel, a copy of
![]() $H_{0}$
or a copy of
$H_{0}$
or a copy of
![]() $T_{0}$
. These contradict Propositions 4.5 to 4.7 (applied to G). We have shown that u, v must be b-dense. Thus,
$T_{0}$
. These contradict Propositions 4.5 to 4.7 (applied to G). We have shown that u, v must be b-dense. Thus,
![]() $I \subset D_{u} \cup \mathopen{}\left\{u\right\}\mathclose{}$
.
$I \subset D_{u} \cup \mathopen{}\left\{u\right\}\mathclose{}$
.
On the other hand, by the definition of density and Lemma 4.4,
![]() $D_{u} \cup \mathopen{}\left\{u\right\}\mathclose{}$
is an independent set. It contains the maximal independent set I so must equal it.
$D_{u} \cup \mathopen{}\left\{u\right\}\mathclose{}$
is an independent set. It contains the maximal independent set I so must equal it.
Definition 4.9. (b-quasidense) A pair of vertices u, v is b-quasidense if there is a sequence of vertices
![]() $u = d_{1}, d_{2}, \dotsc, d_{k}, d_{k + 1} = v$
such that all pairs
$u = d_{1}, d_{2}, \dotsc, d_{k}, d_{k + 1} = v$
such that all pairs
![]() $d_{i}, d_{i + 1}$
are b-dense (
$d_{i}, d_{i + 1}$
are b-dense (
![]() $i = 1, 2, \dotsc, k$
).
$i = 1, 2, \dotsc, k$
).
Proposition 4.8 immediately implies that if u, v is b-quasidense and
![]() $u \in I$
, then
$u \in I$
, then
![]() $v \in I$
as well. Now we can finish the proof. It suffices to show that every vertex is either in I or is adjacent to all of I. Indeed, we may then fix
$v \in I$
as well. Now we can finish the proof. It suffices to show that every vertex is either in I or is adjacent to all of I. Indeed, we may then fix
![]() $u \in I$
and note that
$u \in I$
and note that
![]() $G[V(G) \setminus I] = G_{u}$
so
$G[V(G) \setminus I] = G_{u}$
so
![]() $G[V(G) \setminus I]$
is b-colourable. Using a further colour for the independent set I gives a
$G[V(G) \setminus I]$
is b-colourable. Using a further colour for the independent set I gives a
![]() $(b + 1)$
-colouring of G.
$(b + 1)$
-colouring of G.
Suppose instead there is
![]() $u \in I$
and
$u \in I$
and
![]() $v \not \in I$
with u not adjacent to v. In particular, the pair u, v cannot be b-quasidense and so is b-sparse. Thus, from our remarks just preceding Proposition 4.8, there is a
$v \not \in I$
with u not adjacent to v. In particular, the pair u, v cannot be b-quasidense and so is b-sparse. Thus, from our remarks just preceding Proposition 4.8, there is a
![]() $(b - 2)$
-clique K in G such that
$(b - 2)$
-clique K in G such that
![]() $G_{K}$
contains one of the configurations appearing in Figure 5 (with labels u and v possibly swapped) and the pair u, v is 2-sparse in
$G_{K}$
contains one of the configurations appearing in Figure 5 (with labels u and v possibly swapped) and the pair u, v is 2-sparse in
![]() $G_{K}$
.
$G_{K}$
.
Focus on
![]() $G_{K}$
– this graph is 3-colourable so locally bipartite,
$G_{K}$
– this graph is 3-colourable so locally bipartite,
![]() $H_{0}$
-free and
$H_{0}$
-free and
![]() $T_{0}$
-free and the pair u, v is 2-sparse in
$T_{0}$
-free and the pair u, v is 2-sparse in
![]() $G_{K}$
. Also, by Lemma 4.2,
$G_{K}$
. Also, by Lemma 4.2,
![]() $\delta(G_{K}) > (1 - 1/(b - (b - 2) + 1/7)) \cdot \mathopen{}\left\vert G_{K} \right\vert\mathclose{} = 8/15 \cdot \mathopen{}\left\vert G_{K} \right\vert\mathclose{}$
. In the proof of Proposition 3.21, we used these facts alone to show that u, v is quasidense in every configuration appearing in Figure 5. Hence, the pair u, v is quasidense in
$\delta(G_{K}) > (1 - 1/(b - (b - 2) + 1/7)) \cdot \mathopen{}\left\vert G_{K} \right\vert\mathclose{} = 8/15 \cdot \mathopen{}\left\vert G_{K} \right\vert\mathclose{}$
. In the proof of Proposition 3.21, we used these facts alone to show that u, v is quasidense in every configuration appearing in Figure 5. Hence, the pair u, v is quasidense in
![]() $G_{K}$
so is b-quasidense in G. This is our required contradiction.
$G_{K}$
so is b-quasidense in G. This is our required contradiction.
5 a-locally b-partite graphs
In this section, we relate the chromatic profile of a-locally b-partite graphs to the chromatic profile of locally b-partite graphs, making precise our comment in the introduction that to understand a-locally b-partite graphs it seems to be enough to understand locally b-partite graphs. This is elucidated at the end of Section 5.1 and just before Theorem 5.6. Along the way, we will prove Theorems 1.3 and 1.4.
5.1 The first threshold – proving Theorems 1.3 and 1.4
As noted in the introduction, the first interesting threshold is
![]() $\delta_{\chi}(\mathcal{F}_{a,b}, a + b)$
– what values of c guarantee that any a-locally b-partite graph with
$\delta_{\chi}(\mathcal{F}_{a,b}, a + b)$
– what values of c guarantee that any a-locally b-partite graph with
![]() $\delta(G) \geqslant c \mathopen{}\left\vert G \right\vert\mathclose{}$
is
$\delta(G) \geqslant c \mathopen{}\left\vert G \right\vert\mathclose{}$
is
![]() $(a + b)$
-colourable? We already know
$(a + b)$
-colourable? We already know
![]() $\delta_{\chi}(\mathcal{F}_{1,2}, 3) = 4/7$
and
$\delta_{\chi}(\mathcal{F}_{1,2}, 3) = 4/7$
and
![]() $\delta_{\chi}(\mathcal{F}_{1,b}, b + 1) \leqslant 1 - 1/(b + 1/7)$
and will extend these to all values of a. To simplify the statements of our results and make comparisons between different values of a and b, it is helpful to write
$\delta_{\chi}(\mathcal{F}_{1,b}, b + 1) \leqslant 1 - 1/(b + 1/7)$
and will extend these to all values of a. To simplify the statements of our results and make comparisons between different values of a and b, it is helpful to write
and to focus our attention on the
![]() $\gamma_{a, b}$
. As
$\gamma_{a, b}$
. As
![]() $\delta_{\chi}(\mathcal{F}_{a,b}, a + b) \geqslant \delta_{\chi}(\mathcal{F}_{a,b})$
we have, from Theorem 1.2,
$\delta_{\chi}(\mathcal{F}_{a,b}, a + b) \geqslant \delta_{\chi}(\mathcal{F}_{a,b})$
we have, from Theorem 1.2,
We collect some other basic properties of the
![]() $\gamma_{a, b}$
.
$\gamma_{a, b}$
.
Lemma 5.1. For all positive integers a and b the following hold.
-
 $\delta_{\chi}(\mathcal{F}_{a, b+1}, a + b) \leqslant \delta_{\chi}(\mathcal{F}_{a + 1, b}, a + b)$
and so
(3)
$\delta_{\chi}(\mathcal{F}_{a, b+1}, a + b) \leqslant \delta_{\chi}(\mathcal{F}_{a + 1, b}, a + b)$
and so
(3) \begin{equation}\gamma_{a, b + 1} \leqslant \gamma_{a + 1, b}.\end{equation}
\begin{equation}\gamma_{a, b + 1} \leqslant \gamma_{a + 1, b}.\end{equation}
-
 $1/(2 - \delta_{\chi}(\mathcal{F}_{a, b}, a + b)) \leqslant \delta_{\chi}(\mathcal{F}_{a + 1, b}, a + b + 1)$
and so
(4)
$1/(2 - \delta_{\chi}(\mathcal{F}_{a, b}, a + b)) \leqslant \delta_{\chi}(\mathcal{F}_{a + 1, b}, a + b + 1)$
and so
(4) \begin{equation}\gamma_{a, b} \leqslant \gamma_{a + 1, b}.\end{equation}
\begin{equation}\gamma_{a, b} \leqslant \gamma_{a + 1, b}.\end{equation}
Also
![]() $\gamma_{1,2} = 1/3$
and
$\gamma_{1,2} = 1/3$
and
![]() $\gamma_{1, b} \leqslant 1/7$
for all
$\gamma_{1, b} \leqslant 1/7$
for all
![]() $b \geqslant 3$
.
$b \geqslant 3$
.
Proof. In [Reference Illingworth11], it was shown that
![]() $\delta_{\chi}(\mathcal{F}_{1,2},3) = 4/7$
giving
$\delta_{\chi}(\mathcal{F}_{1,2},3) = 4/7$
giving
![]() $\gamma_{1,2} = 1/3$
while, for
$\gamma_{1,2} = 1/3$
while, for
![]() $b \geqslant 3$
, Section 4 showed
$b \geqslant 3$
, Section 4 showed
![]() $\delta_{\chi}(\mathcal{F}_{1,b},b + 1) \leqslant 1 - 1/(b + 1/7)$
so
$\delta_{\chi}(\mathcal{F}_{1,b},b + 1) \leqslant 1 - 1/(b + 1/7)$
so
![]() $\gamma_{1, b} \leqslant 1/7$
.
$\gamma_{1, b} \leqslant 1/7$
.
Now
![]() $\mathcal{F}_{a, b + 1} \subset \mathcal{F}_{a + 1, b}$
from which
$\mathcal{F}_{a, b + 1} \subset \mathcal{F}_{a + 1, b}$
from which
![]() $\delta_{\chi}(\mathcal{F}_{a, b + 1}, a + b) \leqslant \delta_{\chi}(\mathcal{F}_{a + 1, b}, a + b)$
immediately follows. This gives inequality (3).
$\delta_{\chi}(\mathcal{F}_{a, b + 1}, a + b) \leqslant \delta_{\chi}(\mathcal{F}_{a + 1, b}, a + b)$
immediately follows. This gives inequality (3).
Finally, let
![]() $d < \delta_{\chi}(\mathcal{F}_{a, b}, a + b)$
: there is an a-locally b-partite graph G with
$d < \delta_{\chi}(\mathcal{F}_{a, b}, a + b)$
: there is an a-locally b-partite graph G with
![]() $\delta(G) \geqslant d \mathopen{}\left\vert G \right\vert\mathclose{}$
and
$\delta(G) \geqslant d \mathopen{}\left\vert G \right\vert\mathclose{}$
and
![]() $\chi(G) > a + b$
. Let G
$\chi(G) > a + b$
. Let G
![]() $^{\prime}$
be G joined to an independent set of size
$^{\prime}$
be G joined to an independent set of size
![]() $\mathopen{}\left\vert G \right\vert\mathclose{} - \delta(G)$
, that is,
$\mathopen{}\left\vert G \right\vert\mathclose{} - \delta(G)$
, that is,
Since G is a-locally b-partite, it is also
![]() $(a + 1)$
-locally
$(a + 1)$
-locally
![]() $(b - 1)$
-partite. From both of these, it follows that G
$(b - 1)$
-partite. From both of these, it follows that G
![]() $^{\prime}$
is
$^{\prime}$
is
![]() $(a + 1)$
-locally b-partite. Also,
$(a + 1)$
-locally b-partite. Also,
![]() $\chi(G') = \chi(G) + 1 > a + b + 1$
, and
$\chi(G') = \chi(G) + 1 > a + b + 1$
, and
so
![]() $\delta_{\chi}(\mathcal{F}_{a + 1, b}, a + b + 1) \geqslant 1/(2 - d)$
. This holds for all
$\delta_{\chi}(\mathcal{F}_{a + 1, b}, a + b + 1) \geqslant 1/(2 - d)$
. This holds for all
![]() $d < \delta_{\chi}(\mathcal{F}_{a, b}, a + b)$
, so
$d < \delta_{\chi}(\mathcal{F}_{a, b}, a + b)$
, so
![]() $\delta_{\chi}(\mathcal{F}_{a + 1, b}, a + b + 1) \geqslant 1/(2 - \delta_{\chi}(\mathcal{F}_{a, b}, a + b))$
. Thus,
$\delta_{\chi}(\mathcal{F}_{a + 1, b}, a + b + 1) \geqslant 1/(2 - \delta_{\chi}(\mathcal{F}_{a, b}, a + b))$
. Thus,
 \begin{equation*}1 - \frac{1}{a + b + \gamma_{a + 1, b}} \geqslant \frac{1}{1 + \frac{1}{a + b - 1 + \gamma_{a, b}}} = \frac{a + b - 1 + \gamma_{a, b}}{a + b + \gamma_{a, b}} = 1 - \frac{1}{a + b + \gamma_{a, b}},\end{equation*}
\begin{equation*}1 - \frac{1}{a + b + \gamma_{a + 1, b}} \geqslant \frac{1}{1 + \frac{1}{a + b - 1 + \gamma_{a, b}}} = \frac{a + b - 1 + \gamma_{a, b}}{a + b + \gamma_{a, b}} = 1 - \frac{1}{a + b + \gamma_{a, b}},\end{equation*}
and so
![]() $\gamma_{a + 1, b} \geqslant \gamma_{a, b}$
, as required.
$\gamma_{a + 1, b} \geqslant \gamma_{a, b}$
, as required.
Inequality (4) gives a lower bound for
![]() $\gamma_{a + 1, b}$
in terms of
$\gamma_{a + 1, b}$
in terms of
![]() $\gamma_{a, b}$
. The next lemma, which lies at the heart of our analysis, gives an upper bound.
$\gamma_{a, b}$
. The next lemma, which lies at the heart of our analysis, gives an upper bound.
Lemma 5.2. For all positive integers a and b,
Proof. The left-hand inequality is just inequality (4). Let
![]() $\gamma = \max \mathopen{}\left\{\gamma_{a, b}, \gamma_{1, a + b}\right\}\mathclose{}$
. Let G be an
$\gamma = \max \mathopen{}\left\{\gamma_{a, b}, \gamma_{1, a + b}\right\}\mathclose{}$
. Let G be an
![]() $(a + 1)$
-locally b-partite graph with
$(a + 1)$
-locally b-partite graph with
It suffices to show that
![]() $\chi(G) \leqslant a + b + 1$
as then
$\chi(G) \leqslant a + b + 1$
as then
Fix any
![]() $u \in V(G)$
and consider
$u \in V(G)$
and consider
![]() $G_{u}$
:
$G_{u}$
:
![]() $G_{u}$
is an a-locally b-partite graph with
$G_{u}$
is an a-locally b-partite graph with
by the lifting lemma, Lemma 4.2. But
![]() $\gamma \geqslant \gamma_{a, b}$
so
$\gamma \geqslant \gamma_{a, b}$
so
and hence
![]() $G_{u}$
is
$G_{u}$
is
![]() $(a + b)$
-colourable. Thus, the graph G is locally
$(a + b)$
-colourable. Thus, the graph G is locally
![]() $(a + b)$
-partite. Also
$(a + b)$
-partite. Also
![]() $\gamma \geqslant \gamma_{1, a + b}$
, so
$\gamma \geqslant \gamma_{1, a + b}$
, so
Thus, G is
![]() $(a + b + 1)$
-colourable.
$(a + b + 1)$
-colourable.
From this, one can immediately deduce Theorems 1.3 and 1.4.
Corollary 5.3. (Theorems 1.3 and 1.4) For all positive integers a and for all
![]() $b \geqslant 3$
,
$b \geqslant 3$
,
and so
Proof. From Lemma 5.1,
![]() $\gamma_{1, 2} = 1/3$
and
$\gamma_{1, 2} = 1/3$
and
![]() $\gamma_{1, b} \leqslant 1/7$
for any
$\gamma_{1, b} \leqslant 1/7$
for any
![]() $b \geqslant 3$
. By Lemma 5.2, for any a and any
$b \geqslant 3$
. By Lemma 5.2, for any a and any
![]() $b \geqslant 2$
,
$b \geqslant 2$
,
An easy induction gives
![]() $\gamma_{a, 2} = 1/3$
for all a and
$\gamma_{a, 2} = 1/3$
for all a and
![]() $\gamma_{a, b} \leqslant 1/7$
for any
$\gamma_{a, b} \leqslant 1/7$
for any
![]() $b \geqslant 3$
.
$b \geqslant 3$
.
Note that inequalities (3) and (4) give
for all
![]() $b \leqslant b' \leqslant a + b - 1$
. In line with our inductive arguments in Section 4, we believe that in fact
$b \leqslant b' \leqslant a + b - 1$
. In line with our inductive arguments in Section 4, we believe that in fact
![]() $\gamma_{1, b} \geqslant \gamma_{1, b + 1}$
for all b. If this were true, then
$\gamma_{1, b} \geqslant \gamma_{1, b + 1}$
for all b. If this were true, then
![]() $\gamma_{a, b} \geqslant \gamma_{1, a + b}$
, and so Lemma 5.2 would give
$\gamma_{a, b} \geqslant \gamma_{1, a + b}$
, and so Lemma 5.2 would give
![]() $\gamma_{a, b} = \gamma_{a + 1, b}$
for all a, b. Of course, this implies
$\gamma_{a, b} = \gamma_{a + 1, b}$
for all a, b. Of course, this implies
![]() $\gamma_{a, b} = \gamma_{1, b}$
and so
$\gamma_{a, b} = \gamma_{1, b}$
and so
![]() $\delta_{\chi}(\mathcal{F}_{a, b}, a + b)$
would be determined by
$\delta_{\chi}(\mathcal{F}_{a, b}, a + b)$
would be determined by
![]() $\delta_{\chi}(\mathcal{F}_{1, b}, b + 1)$
– a particular manifestation of our aforementioned belief that to understand a-locally b-partite graphs, we should focus on locally b-partite graphs. It also highlights the following question.
$\delta_{\chi}(\mathcal{F}_{1, b}, b + 1)$
– a particular manifestation of our aforementioned belief that to understand a-locally b-partite graphs, we should focus on locally b-partite graphs. It also highlights the following question.
Question 5.4. Is the sequence
![]() $\gamma_{1, b}$
non-increasing in b?
$\gamma_{1, b}$
non-increasing in b?
5.2 a-locally bipartite graphs
One could replicate the elementary approach of the previous section to try to evaluate
![]() $\delta_{\chi}(\mathcal{F}_{a, b}, k)$
for
$\delta_{\chi}(\mathcal{F}_{a, b}, k)$
for
![]() $k > a + b$
. Indeed, one might define
$k > a + b$
. Indeed, one might define
![]() $\gamma_{a, b, m}$
by
$\gamma_{a, b, m}$
by
so that
![]() $\gamma_{a, b, 0} = \gamma_{a, b}$
. Many of the properties of the
$\gamma_{a, b, 0} = \gamma_{a, b}$
. Many of the properties of the
![]() $\gamma_{a, b}$
pass over: the
$\gamma_{a, b}$
pass over: the
![]() $\gamma_{a, b, m}$
are non-negative (and, in fact,
$\gamma_{a, b, m}$
are non-negative (and, in fact,
![]() $\lim_{m \rightarrow \infty} \gamma_{a, b, m} = 0$
) and both inequalities (3) and (4) extend easily (
$\lim_{m \rightarrow \infty} \gamma_{a, b, m} = 0$
) and both inequalities (3) and (4) extend easily (
![]() $\gamma_{a, b + 1, m} \leqslant \gamma_{a + 1, b, m}$
and
$\gamma_{a, b + 1, m} \leqslant \gamma_{a + 1, b, m}$
and
![]() $\gamma_{a, b, m} \leqslant \gamma_{a + 1, b, m}$
). However, there seems to be no argument to produce inequality (5) or anything similar. A more involved approach would be required.
$\gamma_{a, b, m} \leqslant \gamma_{a + 1, b, m}$
). However, there seems to be no argument to produce inequality (5) or anything similar. A more involved approach would be required.
The next threshold to consider is
![]() $\delta_{\chi}(\mathcal{F}_{a, b}, a + b + 1)$
. For locally bipartite graphs, we showed
$\delta_{\chi}(\mathcal{F}_{a, b}, a + b + 1)$
. For locally bipartite graphs, we showed
![]() $\delta_{\chi}(\mathcal{F}_{1, 2}, 4) \leqslant 6/11$
and had many structural results (some of which we will extend). For
$\delta_{\chi}(\mathcal{F}_{1, 2}, 4) \leqslant 6/11$
and had many structural results (some of which we will extend). For
![]() $b \geqslant 3$
, we know very little about
$b \geqslant 3$
, we know very little about
![]() $\delta_{\chi}(\mathcal{F}_{1, b}, b + 2)$
beyond it being at least
$\delta_{\chi}(\mathcal{F}_{1, b}, b + 2)$
beyond it being at least
![]() $\delta_{\chi}(\mathcal{F}_{1, b}) = 1 - 1/b$
and at most
$\delta_{\chi}(\mathcal{F}_{1, b}) = 1 - 1/b$
and at most
![]() $\delta_{\chi}(\mathcal{F}_{1, b}, b + 1) \leqslant 1 - 1/(b + 1/7)$
. The question for
$\delta_{\chi}(\mathcal{F}_{1, b}, b + 1) \leqslant 1 - 1/(b + 1/7)$
. The question for
![]() $b = 3$
is of particular interest. Tantalisingly, the complement of the 9-cycle is locally tripartite, 5-chromatic and has minimum degree
$b = 3$
is of particular interest. Tantalisingly, the complement of the 9-cycle is locally tripartite, 5-chromatic and has minimum degree
![]() $6 = 2/3 \cdot 9$
.
$6 = 2/3 \cdot 9$
.
Question 5.5. Is there a locally tripartite graph G with minimum degree greater than
![]() $2/3 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
which is not 4-colourable?
$2/3 \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
which is not 4-colourable?
We now focus on a-locally bipartite graphs. The following theorem, which will be essential for extending the Andrásfai-Erdős-Sós theorem [Reference Illingworth12], should be compared to Theorem 3.1 – again we see that the key to understanding a-locally bipartite graphs is to understand locally bipartite ones. The proof is an induction combining our results for locally bipartite (Theorem 3.1) and locally b-partite (Theorem 1.3) graphs.
Theorem 5.6. (a-locally bipartite graphs) Let G be an a-locally bipartite graph.
-
a. If
 $\delta(G) > (1 - 1/(a + 4/3)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is
$\delta(G) > (1 - 1/(a + 4/3)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is
 $(a + 2)$
-colourable. Suitable blow-ups of
$(a + 2)$
-colourable. Suitable blow-ups of
 $K_{a - 1} + \overline{C}_{7}$
show that this is tight.
$K_{a - 1} + \overline{C}_{7}$
show that this is tight. -
b. If
 $\delta(G) > (1 - 1/(a + 5/4)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is either
$\delta(G) > (1 - 1/(a + 5/4)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is either
 $(a + 2)$
-colourable or contains
$(a + 2)$
-colourable or contains
 $K_{a - 1} + \overline{C}_{7}$
.
$K_{a - 1} + \overline{C}_{7}$
. -
c. If
 $\delta(G) > (1 - 1/(a + 6/5)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is either
$\delta(G) > (1 - 1/(a + 6/5)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is either
 $(a + 2)$
-colourable or contains
$(a + 2)$
-colourable or contains
 $K_{a - 1} + \overline{C}_{7}$
or
$K_{a - 1} + \overline{C}_{7}$
or
 $K_{a - 1} + H_{2}^{+}$
.
$K_{a - 1} + H_{2}^{+}$
. -
d. If
 $\delta(G) > (1 - 1/(a + 7/6)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is either
$\delta(G) > (1 - 1/(a + 7/6)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is either
 $(a + 2)$
-colourable or contains
$(a + 2)$
-colourable or contains
 $K_{a - 1} + H_{2}$
.
$K_{a - 1} + H_{2}$
. -
e. If
 $\delta(G) > (1 - 1/(a + 8/7)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is either
$\delta(G) > (1 - 1/(a + 8/7)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
, then G is either
 $(a + 2)$
-colourable or contains
$(a + 2)$
-colourable or contains
 $K_{a - 1} + H_{2}$
or
$K_{a - 1} + H_{2}$
or
 $K_{a - 1} + T_{0}$
.
$K_{a - 1} + T_{0}$
.
Proof. The graph
![]() $K_{a - 1} + \overline{C}_{7}$
is a-locally bipartite with chromatic number
$K_{a - 1} + \overline{C}_{7}$
is a-locally bipartite with chromatic number
![]() $a + 3$
. Hence,
$a + 3$
. Hence,
![]() $K_{a - 1}(3) + \overline{C}_{7}$
also has these properties and is, furthermore,
$K_{a - 1}(3) + \overline{C}_{7}$
also has these properties and is, furthermore,
![]() $(3a + 1)$
-regular with
$(3a + 1)$
-regular with
![]() $3a + 4$
vertices. Thus, balanced blow-ups of
$3a + 4$
vertices. Thus, balanced blow-ups of
![]() $K_{a - 1}(3) + \overline{C}_{7}$
give the tightness of the first bullet point. Proving everything else is a simple induction on a (with Theorem 3.1 covering the base case). Indeed, we will just demonstrate it for part e. Let G be an a-locally bipartite graph with
$K_{a - 1}(3) + \overline{C}_{7}$
give the tightness of the first bullet point. Proving everything else is a simple induction on a (with Theorem 3.1 covering the base case). Indeed, we will just demonstrate it for part e. Let G be an a-locally bipartite graph with
![]() $\delta(G) > (1 - 1/(a + 8/7)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. Fix any vertex u of G and consider
$\delta(G) > (1 - 1/(a + 8/7)) \cdot \mathopen{}\left\vert G \right\vert\mathclose{}$
. Fix any vertex u of G and consider
![]() $G_{u}$
: this is
$G_{u}$
: this is
![]() $(a - 1)$
-locally bipartite, and by Lemma 4.2,
$(a - 1)$
-locally bipartite, and by Lemma 4.2,
![]() $\delta(G_{u}) > (1 - 1/(a - 1 + 8/7)) \cdot \mathopen{}\left\vert G_{u} \right\vert\mathclose{}$
. By induction, either
$\delta(G_{u}) > (1 - 1/(a - 1 + 8/7)) \cdot \mathopen{}\left\vert G_{u} \right\vert\mathclose{}$
. By induction, either
![]() $G_{u}$
contains one of
$G_{u}$
contains one of
![]() $K_{a - 2} + H_{2}$
,
$K_{a - 2} + H_{2}$
,
![]() $K_{a - 2} + T_{0}$
or is
$K_{a - 2} + T_{0}$
or is
![]() $(a + 1)$
-colourable. If there is some vertex u with
$(a + 1)$
-colourable. If there is some vertex u with
![]() $G_{u}$
not
$G_{u}$
not
![]() $(a + 1)$
-colourable, then G contains one of
$(a + 1)$
-colourable, then G contains one of
![]() $K_{a - 1} + H_{2}$
,
$K_{a - 1} + H_{2}$
,
![]() $K_{a - 1} + T_{0}$
. Otherwise, G is locally
$K_{a - 1} + T_{0}$
. Otherwise, G is locally
![]() $(a + 1)$
-partite. But, by Theorem 1.3,
$(a + 1)$
-partite. But, by Theorem 1.3,
so G is
![]() $(a + 2)$
-colourable, as required.
$(a + 2)$
-colourable, as required.
Acknowledgement
It is a pleasure to thank Andrew Thomason for many helpful discussions. I am grateful to the anonymous referees for their careful reading and excellent suggestions for improving the presentation.
A Verifying Figure 3
In this appendix, we verify Figure 3 which, for convenience, we display again here.

The reader will recall that full arrows represent containment and dashed arrows represent homomorphisms. Furthermore, H is homomorphic to G in the diagram if there is a sequence of arrows starting at H and ending at G.
All the containments are clear. The following figure gives a homomorphism from
![]() $H_{1}^{++}$
to
$H_{1}^{++}$
to
![]() $H_{2}^{+}$
: the left diagram is a labelling of the vertices of
$H_{2}^{+}$
: the left diagram is a labelling of the vertices of
![]() $H_{1}^{++}$
and the right diagram shows the images of those vertices under the map.
$H_{1}^{++}$
and the right diagram shows the images of those vertices under the map.

The following figures gives a homomorphism from
![]() $T_{0}$
to
$T_{0}$
to
![]() $H_{2}^{+}$
: the left diagram is a labelling of the vertices of
$H_{2}^{+}$
: the left diagram is a labelling of the vertices of
![]() $T_{0,}$
and the right diagram shows the images of those vertices under the map.
$T_{0,}$
and the right diagram shows the images of those vertices under the map.

In particular, all arrows in Figure 3 are correct. We need to show that further arrows could not be added. There are some subtleties in our notation that we now elucidate. Given a homomorphism
![]() $\varphi \colon H \rightarrow G$
, we say
$\varphi \colon H \rightarrow G$
, we say
![]() $\varphi$
is surjective or injective if the map
$\varphi$
is surjective or injective if the map
![]() $\varphi \colon V(H) \rightarrow V(G)$
is surjective or injective, respectively. Note that
$\varphi \colon V(H) \rightarrow V(G)$
is surjective or injective, respectively. Note that
![]() $\varphi$
being injective implies that H is actually a subgraph of G. By
$\varphi$
being injective implies that H is actually a subgraph of G. By
![]() $\varphi(H),$
we mean the graph on vertex set
$\varphi(H),$
we mean the graph on vertex set
![]() $\varphi(V(H))$
and edge set
$\varphi(V(H))$
and edge set
![]() $\varphi(E(H))$
. In particular, this is a spanning subgraph of
$\varphi(E(H))$
. In particular, this is a spanning subgraph of
![]() $G[\varphi(V(H))]$
but it may not have all the edges of
$G[\varphi(V(H))]$
but it may not have all the edges of
![]() $G[\varphi(V(H))]$
. We make frequent use of the fact that
$G[\varphi(V(H))]$
. We make frequent use of the fact that
![]() $\chi(\varphi(H)) \geqslant \chi(H)$
.
$\chi(\varphi(H)) \geqslant \chi(H)$
.
We first deal with left-hand side (
![]() $H_{0} \rightarrow H_{1} \rightarrow H_{2} \rightarrow \overline{C}_{7}$
) of the figure: we need to show that
$H_{0} \rightarrow H_{1} \rightarrow H_{2} \rightarrow \overline{C}_{7}$
) of the figure: we need to show that
![]() $\overline{C}_{7} \nrightarrow H_{2}$
,
$\overline{C}_{7} \nrightarrow H_{2}$
,
![]() $H_{2} \nrightarrow H_{1}$
and
$H_{2} \nrightarrow H_{1}$
and
![]() $H_{1} \nrightarrow H_{0}$
. The arguments are very similar, making use of the fact that
$H_{1} \nrightarrow H_{0}$
. The arguments are very similar, making use of the fact that
![]() $H_{0}$
,
$H_{0}$
,
![]() $H_{1}$
,
$H_{1}$
,
![]() $H_{2}$
and
$H_{2}$
and
![]() $\overline{C}_{7}$
are all vertex-critical 4-chromatic graphs on seven vertices, so we only give the explicit proof for
$\overline{C}_{7}$
are all vertex-critical 4-chromatic graphs on seven vertices, so we only give the explicit proof for
![]() $H_{2} \nrightarrow H_{1}$
.
$H_{2} \nrightarrow H_{1}$
.
Proposition A.1. The graph
![]() $H_{2}$
is not homomorphic to
$H_{2}$
is not homomorphic to
![]() $H_{1}$
.
$H_{1}$
.
Proof. Suppose there is a homomorphism
![]() $\varphi \colon H_{2} \rightarrow H_{1}$
. Then,
$\varphi \colon H_{2} \rightarrow H_{1}$
. Then,
![]() $\chi(\varphi(H_{2})) \geqslant \chi(H_{2}) = 4$
. Now,
$\chi(\varphi(H_{2})) \geqslant \chi(H_{2}) = 4$
. Now,
![]() $H_{1}$
is a vertex-critical 4-chromatic graph, so
$H_{1}$
is a vertex-critical 4-chromatic graph, so
![]() $\varphi$
is surjective. But
$\varphi$
is surjective. But
![]() $H_{1}$
and
$H_{1}$
and
![]() $H_{2}$
both have seven vertices so
$H_{2}$
both have seven vertices so
![]() $\varphi$
is injective. That is,
$\varphi$
is injective. That is,
![]() $H_{1}$
must contain a copy of
$H_{1}$
must contain a copy of
![]() $H_{2}$
, which is absurd as
$H_{2}$
, which is absurd as
![]() $e(H_{1}) < e(H_{2})$
.
$e(H_{1}) < e(H_{2})$
.
We now know that the left-hand side of Figure 3 is correct and consider how
![]() $H_{2}^{+}$
relates to it. It suffices to show that
$H_{2}^{+}$
relates to it. It suffices to show that
![]() $H_{2}^{+} \nrightarrow \overline{C}_{7}$
and
$H_{2}^{+} \nrightarrow \overline{C}_{7}$
and
![]() $\overline{C}_{7} \nrightarrow H_{2}^{+}$
(note that
$\overline{C}_{7} \nrightarrow H_{2}^{+}$
(note that
![]() $H_{2}^{+} \nrightarrow \overline{C}_{7}$
implies
$H_{2}^{+} \nrightarrow \overline{C}_{7}$
implies
![]() $H_{2}^{+} \nrightarrow H_{2}, H_{1}, H_{0}$
). That
$H_{2}^{+} \nrightarrow H_{2}, H_{1}, H_{0}$
). That
![]() $H_{2}^{+}$
is not homomorphic to
$H_{2}^{+}$
is not homomorphic to
![]() $\overline{C}_{7}$
and vice versa follows from the next lemma, which appeared in [Reference Illingworth11] – both
$\overline{C}_{7}$
and vice versa follows from the next lemma, which appeared in [Reference Illingworth11] – both
![]() $\overline{C}_{7}$
and
$\overline{C}_{7}$
and
![]() $H_{2}^{+}$
are edge-maximal locally bipartite graphs and neither is a subgraph of the other (
$H_{2}^{+}$
are edge-maximal locally bipartite graphs and neither is a subgraph of the other (
![]() $\overline{C}_{7}$
has fewer vertices than
$\overline{C}_{7}$
has fewer vertices than
![]() $H_{2}^{+}$
and
$H_{2}^{+}$
and
![]() $H_{2}^{+}$
does not have seven vertices all of degree at least four).
$H_{2}^{+}$
does not have seven vertices all of degree at least four).
Lemma A.2. Let F be an edge-maximal locally bipartite graph in which no two neighbourhoods are the same. Let F be homomorphic to a locally bipartite graph G. Then, F is an induced subgraph of G.
Next, we relate
![]() $H_{1}^{++}$
to the diagram. It suffices to show that
$H_{1}^{++}$
to the diagram. It suffices to show that
![]() $H_{1}^{++} \nrightarrow \overline{C}_{7}$
and
$H_{1}^{++} \nrightarrow \overline{C}_{7}$
and
![]() $H_{2} \nrightarrow H_{1}^{++}$
(note that
$H_{2} \nrightarrow H_{1}^{++}$
(note that
![]() $H_{1}^{++} \nrightarrow \overline{C}_{7}$
implies
$H_{1}^{++} \nrightarrow \overline{C}_{7}$
implies
![]() $H_{1}^{++} \nrightarrow H_{2}, H_{1}, H_{0}$
while
$H_{1}^{++} \nrightarrow H_{2}, H_{1}, H_{0}$
while
![]() $H_{2} \nrightarrow H_{1}^{++}$
implies
$H_{2} \nrightarrow H_{1}^{++}$
implies
![]() $\overline{C}_{7} \nrightarrow H_{1}^{++}$
and
$\overline{C}_{7} \nrightarrow H_{1}^{++}$
and
![]() $H_{2}^{+} \nrightarrow H_{1}^{++}$
).
$H_{2}^{+} \nrightarrow H_{1}^{++}$
).
Proposition A.3. The graph
![]() $H_{1}^{++}$
is not homomorphic to
$H_{1}^{++}$
is not homomorphic to
![]() $\overline{C}_{7}$
.
$\overline{C}_{7}$
.
Proof. Suppose there is a homomorphism
![]() $\varphi \colon H_{1}^{++} \rightarrow \overline{C}_{7}$
. Label the copy of
$\varphi \colon H_{1}^{++} \rightarrow \overline{C}_{7}$
. Label the copy of
![]() $H_{1}^{++}$
as shown below and let
$H_{1}^{++}$
as shown below and let
![]() $A = \mathopen{}\left\{a_{0}, a_{1}, \dotsc, a_{6}\right\}\mathclose{}$
so
$A = \mathopen{}\left\{a_{0}, a_{1}, \dotsc, a_{6}\right\}\mathclose{}$
so
![]() $H_{1}^{++}[A]$
is a copy of
$H_{1}^{++}[A]$
is a copy of
![]() $H_{1}$
. Note that
$H_{1}$
. Note that
![]() $\chi(\varphi(H_{1}^{++}[A])) \geqslant \chi(H_{1}^{++}[A]) = 4$
and
$\chi(\varphi(H_{1}^{++}[A])) \geqslant \chi(H_{1}^{++}[A]) = 4$
and
![]() $\overline{C}_{7}$
is a vertex-critical 4-chromatic graph, so the restriction of
$\overline{C}_{7}$
is a vertex-critical 4-chromatic graph, so the restriction of
![]() $\varphi$
to A is a surjection onto
$\varphi$
to A is a surjection onto
![]() $\overline{C}_{7}$
and so
$\overline{C}_{7}$
and so
![]() $\varphi(a_{0}), \varphi(a_{1}), \dotsc, \varphi(a_{6})$
are all distinct.
$\varphi(a_{0}), \varphi(a_{1}), \dotsc, \varphi(a_{6})$
are all distinct.

Now,
![]() $a_{0}$
has degree 6 while
$a_{0}$
has degree 6 while
![]() $\varphi(a_{0}) \in \overline{C}_{7}$
only has degree 4. The four neighbours of
$\varphi(a_{0}) \in \overline{C}_{7}$
only has degree 4. The four neighbours of
![]() $\varphi(a_{0})$
are
$\varphi(a_{0})$
are
![]() $\varphi(a_{1}), \varphi(a_{2}), \varphi(a_{5}), \varphi(a_{6})$
and so
$\varphi(a_{1}), \varphi(a_{2}), \varphi(a_{5}), \varphi(a_{6})$
and so
![]() $\varphi(a_{023})$
is one of these. Also,
$\varphi(a_{023})$
is one of these. Also,
![]() $a_{2}$
has degree 5 while
$a_{2}$
has degree 5 while
![]() $\varphi(a_{2})$
only has degree 4. The four neighbours of
$\varphi(a_{2})$
only has degree 4. The four neighbours of
![]() $\varphi(a_{2})$
are
$\varphi(a_{2})$
are
![]() $\varphi(a_{0}), \varphi(a_{1}), \varphi(a_{3}), \varphi(a_{4})$
and so
$\varphi(a_{0}), \varphi(a_{1}), \varphi(a_{3}), \varphi(a_{4})$
and so
![]() $\varphi(a_{023})$
is one of these. Hence,
$\varphi(a_{023})$
is one of these. Hence,
![]() $\varphi(a_{023}) = \varphi(a_{1})$
. Similarly, considering the neighbourhoods of
$\varphi(a_{023}) = \varphi(a_{1})$
. Similarly, considering the neighbourhoods of
![]() $a_{0}$
and
$a_{0}$
and
![]() $a_{5}$
shows that
$a_{5}$
shows that
![]() $\varphi(a_{350}) = \varphi(a_{6})$
. Then,
$\varphi(a_{350}) = \varphi(a_{6})$
. Then,
![]() $\Gamma(\varphi(a_{3}))$
contains
$\Gamma(\varphi(a_{3}))$
contains
which has size 5. This contradicts the 4-regularity of
![]() $\overline{C}_{7}$
.
$\overline{C}_{7}$
.
Proposition A.4. The graph
![]() $H_{2}$
is not homomorphic to
$H_{2}$
is not homomorphic to
![]() $H_{1}^{++}$
.
$H_{1}^{++}$
.
Proof. Suppose there is a homomorphism
![]() $\varphi \colon H_{2} \rightarrow H_{1}^{++}$
. Now,
$\varphi \colon H_{2} \rightarrow H_{1}^{++}$
. Now,
![]() $\chi(\varphi(H_{2})) \geqslant \chi(H_{2}) = 4$
and any 6-vertex subgraph of
$\chi(\varphi(H_{2})) \geqslant \chi(H_{2}) = 4$
and any 6-vertex subgraph of
![]() $H_{1}^{++}$
is 3-colourable (it is homomorphic to some 6-vertex subgraph of
$H_{1}^{++}$
is 3-colourable (it is homomorphic to some 6-vertex subgraph of
![]() $H_{2}^{+}$
) so
$H_{2}^{+}$
) so
![]() $\varphi$
must be injective. Thus,
$\varphi$
must be injective. Thus,
![]() $H_{1}^{++}$
contains
$H_{1}^{++}$
contains
![]() $H_{2}$
. But
$H_{2}$
. But
![]() $H_{1}^{++}$
only has 4 vertices of degree at least 4 while
$H_{1}^{++}$
only has 4 vertices of degree at least 4 while
![]() $H_{2}$
has 5 vertices of degree 4.
$H_{2}$
has 5 vertices of degree 4.
Finally, we relate
![]() $T_{0}$
to the diagram. It suffices to show that
$T_{0}$
to the diagram. It suffices to show that
![]() $H_{0} \nrightarrow T_{0}$
,
$H_{0} \nrightarrow T_{0}$
,
![]() $T_{0} \nrightarrow \overline{C}_{7}$
and
$T_{0} \nrightarrow \overline{C}_{7}$
and
![]() $T_{0} \nrightarrow H_{1}^{++}$
(note that
$T_{0} \nrightarrow H_{1}^{++}$
(note that
![]() $H_{0} \nrightarrow T_{0}$
implies that no other graph in the diagram is homomorphic to
$H_{0} \nrightarrow T_{0}$
implies that no other graph in the diagram is homomorphic to
![]() $T_{0}$
while
$T_{0}$
while
![]() $T_{0} \nrightarrow \overline{C}_{7}$
implies that
$T_{0} \nrightarrow \overline{C}_{7}$
implies that
![]() $T_{0} \nrightarrow H_{0}, H_{1}, H_{2}$
). We use the following labelling of the copy of
$T_{0} \nrightarrow H_{0}, H_{1}, H_{2}$
). We use the following labelling of the copy of
![]() $T_{0}$
in all three proofs.
$T_{0}$
in all three proofs.

Proposition A.5. The graph
![]() $H_{0}$
is not homomorphic to
$H_{0}$
is not homomorphic to
![]() $T_{0}$
.
$T_{0}$
.
Proof. We first claim that any 7-vertex subgraph of
![]() $T_{0}$
is 3-colourable. Let F be a 7-vertex subgraph of
$T_{0}$
is 3-colourable. Let F be a 7-vertex subgraph of
![]() $T_{0}$
. If F contains all the
$T_{0}$
. If F contains all the
![]() $v_{i}$
, then F is a subgraph of a 7-cycle and so is 3-colourable. Otherwise, F is a subgraph of
$v_{i}$
, then F is a subgraph of a 7-cycle and so is 3-colourable. Otherwise, F is a subgraph of
![]() $T_{0} - v_{i}$
for some i. This graph is 3-colourable: 2-colour the remaining
$T_{0} - v_{i}$
for some i. This graph is 3-colourable: 2-colour the remaining
![]() $v_{j}$
with colours 1 and 2, give
$v_{j}$
with colours 1 and 2, give
![]() $u_{1}$
and
$u_{1}$
and
![]() $u_{6}$
colour 3 and then give t colour 1 or 2 (opposite to the colour of
$u_{6}$
colour 3 and then give t colour 1 or 2 (opposite to the colour of
![]() $v_{0}$
if it is present).
$v_{0}$
if it is present).
Suppose there is a homomorphism
![]() $\varphi \colon H_{0} \rightarrow T_{0}$
. Then,
$\varphi \colon H_{0} \rightarrow T_{0}$
. Then,
![]() $\varphi(H_{0})$
is a subgraph of
$\varphi(H_{0})$
is a subgraph of
![]() $T_{0}$
with at most 7 vertices, so is 3-colourable. But then,
$T_{0}$
with at most 7 vertices, so is 3-colourable. But then,
![]() $3 \geqslant \chi(\varphi(H_{0})) \geqslant \chi(H_{0}) = 4$
.
$3 \geqslant \chi(\varphi(H_{0})) \geqslant \chi(H_{0}) = 4$
.
Proposition A.6. The graph
![]() $T_{0}$
is not homomorphic to
$T_{0}$
is not homomorphic to
![]() $\overline{C}_{7}$
.
$\overline{C}_{7}$
.
Proof. Suppose
![]() $\varphi \colon T_{0} \rightarrow \overline{C}_{7}$
is a homomorphism. Label the copy of
$\varphi \colon T_{0} \rightarrow \overline{C}_{7}$
is a homomorphism. Label the copy of
![]() $\overline{C}_{7}$
as follows.
$\overline{C}_{7}$
as follows.

Without loss of generality, we may assume
![]() $\varphi(u_{1}) = a_{0}$
. The common neighbourhood
$\varphi(u_{1}) = a_{0}$
. The common neighbourhood
![]() $\Gamma(u_{1}, u_{6})$
contains the edge
$\Gamma(u_{1}, u_{6})$
contains the edge
![]() $tv_{0}$
, so
$tv_{0}$
, so
![]() $\Gamma(\varphi(u_{1}), \varphi(u_{6}))$
contains an edge and so
$\Gamma(\varphi(u_{1}), \varphi(u_{6}))$
contains an edge and so
![]() $\varphi(u_{6}) \in \mathopen{}\left\{a_{0}, a_{3}, a_{4}\right\}\mathclose{}$
. By symmetry, we may assume
$\varphi(u_{6}) \in \mathopen{}\left\{a_{0}, a_{3}, a_{4}\right\}\mathclose{}$
. By symmetry, we may assume
![]() $\varphi(u_{6}) \in \mathopen{}\left\{a_{0}, a_{3}\right\}\mathclose{}$
.
$\varphi(u_{6}) \in \mathopen{}\left\{a_{0}, a_{3}\right\}\mathclose{}$
.
First suppose that
![]() $\varphi(u_{6}) = a_{0}$
. Then,
$\varphi(u_{6}) = a_{0}$
. Then,
However,
![]() $v_{0}v_{1}\dotsc v_{6}$
form a 7-cycle which is 3-chromatic, while
$v_{0}v_{1}\dotsc v_{6}$
form a 7-cycle which is 3-chromatic, while
![]() $\Gamma(a_{0})$
is a path of length 3 (which is bipartite).
$\Gamma(a_{0})$
is a path of length 3 (which is bipartite).
Now suppose that
![]() $\varphi(u_{6}) = a_{3}$
. The edge
$\varphi(u_{6}) = a_{3}$
. The edge
![]() $tv_{0}$
is in
$tv_{0}$
is in
![]() $\Gamma(u_{1}, u_{6})$
so
$\Gamma(u_{1}, u_{6})$
so
![]() $\varphi(t)\varphi(v_{0})$
must be an edge in
$\varphi(t)\varphi(v_{0})$
must be an edge in
![]() $\Gamma(a_{0}, a_{3})$
. In particular,
$\Gamma(a_{0}, a_{3})$
. In particular,
![]() $\mathopen{}\left\{\varphi(t), \varphi(v_{0})\right\}\mathclose{} = \mathopen{}\left\{a_{1}, a_{2}\right\}\mathclose{}$
. By symmetry, we may assume that
$\mathopen{}\left\{\varphi(t), \varphi(v_{0})\right\}\mathclose{} = \mathopen{}\left\{a_{1}, a_{2}\right\}\mathclose{}$
. By symmetry, we may assume that
![]() $\varphi(v_{0}) = a_{1}$
. Now
$\varphi(v_{0}) = a_{1}$
. Now
![]() $v_{1} \in \Gamma(v_{0}, u_{6})$
, so
$v_{1} \in \Gamma(v_{0}, u_{6})$
, so
![]() $\varphi(v_{1}) \in \Gamma(a_{1}, a_{3})$
and so
$\varphi(v_{1}) \in \Gamma(a_{1}, a_{3})$
and so
![]() $\varphi(v_{1}) = a_{2}$
. Next,
$\varphi(v_{1}) = a_{2}$
. Next,
![]() $v_{2} \in \Gamma(u_{1}, u_{6}, v_{1})$
, so
$v_{2} \in \Gamma(u_{1}, u_{6}, v_{1})$
, so
![]() $\varphi(v_{2}) \in \Gamma(a_{0}, a_{3}, a_{2})$
and so
$\varphi(v_{2}) \in \Gamma(a_{0}, a_{3}, a_{2})$
and so
![]() $\varphi(v_{2}) = a_{1}$
. Working in this way round the outer 7-cycle gives
$\varphi(v_{2}) = a_{1}$
. Working in this way round the outer 7-cycle gives
![]() $\varphi(v_{3}) = a_{2}$
,
$\varphi(v_{3}) = a_{2}$
,
![]() $\varphi(v_{4}) = a_{1}$
and
$\varphi(v_{4}) = a_{1}$
and
![]() $\varphi(v_{5}) = a_{2}$
. Finally,
$\varphi(v_{5}) = a_{2}$
. Finally,
![]() $v_{6} \in \Gamma(u_{1}, v_{0}, v_{5})$
and so
$v_{6} \in \Gamma(u_{1}, v_{0}, v_{5})$
and so
![]() $\varphi(v_{6}) \in \Gamma(a_{0}, a_{1}, a_{2}) = \varnothing$
, which is a contradiction.
$\varphi(v_{6}) \in \Gamma(a_{0}, a_{1}, a_{2}) = \varnothing$
, which is a contradiction.
Proposition A.7. The graph
![]() $T_{0}$
is not homomorphic to
$T_{0}$
is not homomorphic to
![]() $H_{1}^{++}$
.
$H_{1}^{++}$
.
Proof. Suppose
![]() $\varphi \colon T_{0} \rightarrow H_{1}^{++}$
is a homomorphism. If x, y is a dense pair (see Definition 3.5) of vertices in
$\varphi \colon T_{0} \rightarrow H_{1}^{++}$
is a homomorphism. If x, y is a dense pair (see Definition 3.5) of vertices in
![]() $T_{0}$
, then
$T_{0}$
, then
![]() $\Gamma(x, y)$
contains an edge, so
$\Gamma(x, y)$
contains an edge, so
![]() $\Gamma(\varphi(x), \varphi(y))$
contains an edge and so either
$\Gamma(\varphi(x), \varphi(y))$
contains an edge and so either
![]() $\varphi(x) = \varphi(y)$
or
$\varphi(x) = \varphi(y)$
or
![]() $\varphi(x), \varphi(y)$
is a dense pair in
$\varphi(x), \varphi(y)$
is a dense pair in
![]() $H_{1}^{++}$
.
$H_{1}^{++}$
.
For a graph G, let
![]() $\mathcal{D}G$
be the graph with vertex set V(G) and with vertices x and y adjacent if x, y is a dense pair in G. The previous paragraph shows that
$\mathcal{D}G$
be the graph with vertex set V(G) and with vertices x and y adjacent if x, y is a dense pair in G. The previous paragraph shows that
![]() $\varphi$
maps a connected set of vertices in
$\varphi$
maps a connected set of vertices in
![]() $\mathcal{D}T_{0}$
to a connected set in
$\mathcal{D}T_{0}$
to a connected set in
![]() $\mathcal{D}H_{1}^{++}$
. The graphs
$\mathcal{D}H_{1}^{++}$
. The graphs
![]() $\mathcal{D}T_{0}$
and
$\mathcal{D}T_{0}$
and
![]() $\mathcal{D}H_{1}^{++}$
are displayed below (we have used the same labelling of the vertices of
$\mathcal{D}H_{1}^{++}$
are displayed below (we have used the same labelling of the vertices of
![]() $H_{1}^{++}$
as in Proposition A.3).
$H_{1}^{++}$
as in Proposition A.3).

Let C be the 8-cycle
![]() $v_{0}v_{2}v_{4}v_{6}tv_{1}v_{3}v_{5}$
of
$v_{0}v_{2}v_{4}v_{6}tv_{1}v_{3}v_{5}$
of
![]() $\mathcal{D}T_{0}$
and so
$\mathcal{D}T_{0}$
and so
![]() $\varphi(C)$
is connected in
$\varphi(C)$
is connected in
![]() $\mathcal{D}H_{1}^{++}$
. If
$\mathcal{D}H_{1}^{++}$
. If
![]() $\varphi(C)$
meets
$\varphi(C)$
meets
![]() $\mathopen{}\left\{a_{0}, a_{3}\right\}\mathclose{}$
, then
$\mathopen{}\left\{a_{0}, a_{3}\right\}\mathclose{}$
, then
![]() $\mathopen{}\left\vert \varphi(C) \right\vert\mathclose{} \leqslant 2$
and so
$\mathopen{}\left\vert \varphi(C) \right\vert\mathclose{} \leqslant 2$
and so
![]() $\mathopen{}\left\vert \varphi(T_{0}) \right\vert\mathclose{} \leqslant 4$
while
$\mathopen{}\left\vert \varphi(T_{0}) \right\vert\mathclose{} \leqslant 4$
while
![]() $\chi(\varphi(T_{0})) \geqslant \chi(T_{0}) = 4$
so
$\chi(\varphi(T_{0})) \geqslant \chi(T_{0}) = 4$
so
![]() $\varphi(T_{0})$
is a 4-clique which is absurd as
$\varphi(T_{0})$
is a 4-clique which is absurd as
![]() $H_{1}^{++}$
is
$H_{1}^{++}$
is
![]() $K_{4}$
-free. Hence,
$K_{4}$
-free. Hence,
![]() $\varphi(C) \subset H_{1}^{++} - \mathopen{}\left\{a_{0}, a_{3}\right\}\mathclose{}$
.
$\varphi(C) \subset H_{1}^{++} - \mathopen{}\left\{a_{0}, a_{3}\right\}\mathclose{}$
.
Now, both
![]() $H_{1}^{++} - a_{0}$
and
$H_{1}^{++} - a_{0}$
and
![]() $H_{1}^{++} - a_{3}$
are 3-colourable (they are both 2-degenerate) and
$H_{1}^{++} - a_{3}$
are 3-colourable (they are both 2-degenerate) and
![]() $\chi(\varphi(T_{0})) \geqslant 4$
, so
$\chi(\varphi(T_{0})) \geqslant 4$
, so
![]() $a_{0}, a_{3} \in \varphi(T_{0})$
. In particular,
$a_{0}, a_{3} \in \varphi(T_{0})$
. In particular,
![]() $\varphi(\mathopen{}\left\{u_{1}, u_{6}\right\}\mathclose{}) = \mathopen{}\left\{a_{0}, a_{3}\right\}\mathclose{}$
. By symmetry, we may assume that
$\varphi(\mathopen{}\left\{u_{1}, u_{6}\right\}\mathclose{}) = \mathopen{}\left\{a_{0}, a_{3}\right\}\mathclose{}$
. By symmetry, we may assume that
![]() $\varphi(u_{1}) = a_{0}$
and
$\varphi(u_{1}) = a_{0}$
and
![]() $\varphi(u_{6}) = a_{3}$
.
$\varphi(u_{6}) = a_{3}$
.
In
![]() $T_{0}$
, the path
$T_{0}$
, the path
![]() $v_{2}v_{3}v_{4}v_{5}$
lies in the common neighbourhood of
$v_{2}v_{3}v_{4}v_{5}$
lies in the common neighbourhood of
![]() $u_{1}$
and
$u_{1}$
and
![]() $u_{6}$
. While, in
$u_{6}$
. While, in
![]() $H_{1}^{++}$
, the common neighbourhood of
$H_{1}^{++}$
, the common neighbourhood of
![]() $a_{0} = \varphi(u_{1})$
,
$a_{0} = \varphi(u_{1})$
,
![]() $a_{3} = \varphi(u_{6})$
consists of two disconnected edges
$a_{3} = \varphi(u_{6})$
consists of two disconnected edges
![]() $a_{2}a_{023}$
and
$a_{2}a_{023}$
and
![]() $a_{5}a_{350}$
. Thus,
$a_{5}a_{350}$
. Thus,
![]() $\mathopen{}\left\{\varphi(v_{2}), \varphi(v_{5})\right\}\mathclose{}$
is either
$\mathopen{}\left\{\varphi(v_{2}), \varphi(v_{5})\right\}\mathclose{}$
is either
![]() $\mathopen{}\left\{a_{2}, a_{023}\right\}\mathclose{}$
or
$\mathopen{}\left\{a_{2}, a_{023}\right\}\mathclose{}$
or
![]() $\mathopen{}\left\{a_{5}, a_{350}\right\}\mathclose{}$
.
$\mathopen{}\left\{a_{5}, a_{350}\right\}\mathclose{}$
.
Back in
![]() $\mathcal{D}T_{0}$
,
$\mathcal{D}T_{0}$
,
![]() $v_{2}v_{0}v_{5}$
is a path, so
$v_{2}v_{0}v_{5}$
is a path, so
![]() $\varphi(v_{2})$
,
$\varphi(v_{2})$
,
![]() $\varphi(v_{5})$
are within distance two of each other in
$\varphi(v_{5})$
are within distance two of each other in
![]() $\mathcal{D}H_{1}^{++}$
. But this is inconsistent with
$\mathcal{D}H_{1}^{++}$
. But this is inconsistent with
![]() $\mathopen{}\left\{\varphi(v_{2}), \varphi(v_{5})\right\}\mathclose{}$
being either
$\mathopen{}\left\{\varphi(v_{2}), \varphi(v_{5})\right\}\mathclose{}$
being either
![]() $\mathopen{}\left\{a_{2}, a_{023}\right\}\mathclose{}$
or
$\mathopen{}\left\{a_{2}, a_{023}\right\}\mathclose{}$
or
![]() $\mathopen{}\left\{a_{5}, a_{350}\right\}\mathclose{}$
.
$\mathopen{}\left\{a_{5}, a_{350}\right\}\mathclose{}$
.