Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-13T09:27:31.300Z Has data issue: false hasContentIssue false
  • English
  • Français

Card guessing with partial feedback

Part of: Combinatorial probability

Published online by Cambridge University Press:  15 June 2021

Persi Diaconis ,
Ron Graham ,
Xiaoyu He  and
Sam Spiro
Persi Diaconis
Affiliation:
Department of Mathematics and Statistics, Stanford University, Stanford, CA94305, USA
Ron Graham
Affiliation:
Department of Computer Science and Engineering, UCSD, La Jolla, CA92093, USA
Xiaoyu He
Affiliation:
Deparment of Mathematics, Stanford University, Stanford, CA94305, USA
Sam Spiro*
Affiliation:
Department of Mathematics, UCSD, La Jolla, CA92093, USA
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider the following experiment: a deck with m copies of n different card types is randomly shuffled, and a guesser attempts to guess the cards sequentially as they are drawn. Each time a guess is made, some amount of ‘feedback’ is given. For example, one could tell the guesser the true identity of the card they just guessed (the complete feedback model) or they could be told nothing at all (the no feedback model). In this paper we explore a partial feedback model, where upon guessing a card, the guesser is only told whether or not their guess was correct. We show in this setting that, uniformly in n, at most 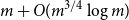$m+O(m^{3/4}\log m)$ cards can be guessed correctly in expectation. This resolves a question of Diaconis and Graham from 1981, where even the 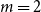$m=2$ case was open.

Keywords

Card GuessingShufflingGames

MSC classification

Primary: 60C05: Combinatorial probability
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 1 , January 2022 , pp. 1 - 20
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research supported by NSF Grant DMS-1954042.

‡

Research supported by NSF Graduate Research Fellowship Grant No. DGE-1656518.

Research supported by NSF Graduate Research Fellowship Grant No. DGE-1650112.

References

Alon, N. and Spencer, J. H. (2004) The Probabilistic Method. John Wiley & Sons.Google Scholar
Blackwell, D. and Hodges, J. L. (1957) Design for the control of selection bias. Ann. Math. Stat. 28 449–460.CrossRefGoogle Scholar
Briggs, W. and Ruppert, D. (2005) Assessing the skill of yes/no predictions. Biometrics 61(3) 799–807.CrossRefGoogle ScholarPubMed
Chung, F., Diaconis, P., Graham, R. and Mallows, C. L. (1981) On the permanents of complements of the direct sum of identity matrices. Adv. Appl. Math. 2(2) 121–137.CrossRefGoogle Scholar
Ciucu, M. (1998) No-feedback card guessing for dovetail shuffles. Ann. Appl. Prob. 8(4) 1251–1269.Google Scholar
Diaconis, P. (1978) Statistical problems in ESP research. Science 201(4351) 131–136.CrossRefGoogle ScholarPubMed
Diaconis, P. and Graham, R. (1981) The analysis of sequential experiments with feedback to subjects. Ann. Stat. 9(1) 3–23.CrossRefGoogle Scholar
Diaconis, P., Graham, R. and Holmes, S. (2001) Statistical Problems Involving Permutations with Restricted Positions , Lecture Notes-Monograph Series, pp. 195–222.CrossRefGoogle Scholar
Diaconis, P., Graham, R. and Spiro, S. (2020). Guessing about Guessing: Practical Strategies for Card Guessing with Feedback. arXiv preprint arXiv:2012.04019.Google Scholar
Efron, B. (1971) Forcing a sequential experiment to be balanced. Biometrika 58(3) 403–417.CrossRefGoogle Scholar
Gural, A., Simper, M. and So, E. (2019) Information Theory in a Card-Guessing Game. https://theinformaticists.com/wp-content/uploads/2019/03/Info_Theory_Project_Card_Guessing_Game.pdf Google Scholar
Liu, P. (2019) Asymptotic analysis of card guessing with feedback. arXiv preprint arXiv:1908.07718.Google Scholar
Pehlivan, L. (2009) On top to random shuffles, no feedback card guessing, and fixed points of permutations. PhD dissertation, University of Southern California.Google Scholar
Proschan, M. (1991) A note on Blackwell and Hodges (1957) and Diaconis and Graham (1981). Ann. Stat. 19(2) 1106–1108.CrossRefGoogle Scholar
Samaniego, F. and Utts, J. (1983) Evaluating performance in continuous experiments with feedback to subjects. Psychometrika 48(2) 195–209.CrossRefGoogle Scholar