Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-06T01:11:30.272Z Has data issue: false hasContentIssue false
  • English
  • Français

Canonical Vertex Partitions

Published online by Cambridge University Press:  03 December 2003

N. W. Sauer
N. W. Sauer*
Affiliation:
Department of Mathematics and Statistics, University of Calgary, 2500 University Drive NW, Calgary, Alberta, T2N 1N4, Canada
*
(e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let σ be a finite relational signature, let 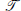be a set of finite complete relational structures of signature σ, and let 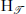be the countable homogeneous relational structure of signature σ which does not embed any of the structures in .

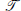When σ consists of at most binary relations and 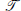is finite, the vertex partition behaviour of 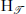is completely analysed, in the sense that it is shown that a canonical partition exists and the size of this partition in terms of the structures in 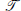is determined. If 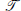is infinite some results are obtained, but a complete analysis is still missing.

Some general results are presented which are intended to be used in further investigations when σ contains relational symbols of arity larger than two or when the set of bounds 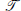is infinite.

Type
Research Article
Information
Combinatorics, Probability and Computing , Volume 12 , Issue 5-6: This issue contains volume twelve, parts five and six , November 2003 , pp. 671 - 704
Copyright
Copyright © Cambridge University Press 2003

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported by NSERC of Canada grant # 691325