Article contents
Bootstrap Percolation in High Dimensions
Published online by Cambridge University Press: 12 August 2010
Abstract
In r-neighbour bootstrap percolation on a graph G, a set of initially infected vertices A ⊂ V(G) is chosen independently at random, with density p, and new vertices are subsequently infected if they have at least r infected neighbours. The set A is said to percolate if eventually all vertices are infected. Our aim is to understand this process on the grid, [n]d, for arbitrary functions n = n(t), d = d(t) and r = r(t), as t → ∞. The main question is to determine the critical probability pc([n]d, r) at which percolation becomes likely, and to give bounds on the size of the critical window. In this paper we study this problem when r = 2, for all functions n and d satisfying d ≫ log n.
The bootstrap process has been extensively studied on [n]d when d is a fixed constant and 2 ⩽ r ⩽ d, and in these cases pc([n]d, r) has recently been determined up to a factor of 1 + o(1) as n → ∞. At the other end of the scale, Balogh and Bollobás determined pc([2]d, 2) up to a constant factor, and Balogh, Bollobás and Morris determined pc([n]d, d) asymptotically if d ≥ (log log n)2+ϵ, and gave much sharper bounds for the hypercube.
Here we prove the following result. Let λ be the smallest positive root of the equation
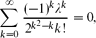 so λ ≈ 1.166. Then
so λ ≈ 1.166. Then
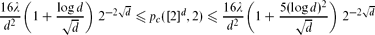 if d is sufficiently large, and moreover
if d is sufficiently large, and moreover
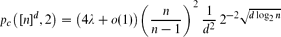 as d → ∞, for every function n = n(d) with d ≫ log n.
as d → ∞, for every function n = n(d) with d ≫ log n.
- Type
- Paper
- Information
- Combinatorics, Probability and Computing , Volume 19 , Issue 5-6: Papers from the 2009 Oberwolfach Meeting on Combinatorics and Probability , November 2010 , pp. 643 - 692
- Copyright
- Copyright © Cambridge University Press 2010
References
- 43
- Cited by


