Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-29T12:02:21.669Z Has data issue: false hasContentIssue false
  • English
  • Français

A Bijective Proof of a Theorem of Knuth

Published online by Cambridge University Press:  21 July 2010

HODA BIDKHORI  and
SHAUNAK KISHORE
HODA BIDKHORI
Affiliation:
Massachusetts Institute of Technology, Massachusetts Avenue, Cambridge, MA 02139, USA (e-mail: [email protected], [email protected])
SHAUNAK KISHORE
Affiliation:
Massachusetts Institute of Technology, Massachusetts Avenue, Cambridge, MA 02139, USA (e-mail: [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The line graph 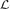G of a directed graph G has a vertex for every edge of G and an edge for every path of length 2 in G. In 1967, Knuth used the Matrix Tree Theorem to prove a formula for the number of spanning trees of 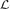G, and he asked for a bijective proof [6]. In this paper, we give a bijective proof of Knuth's formula. As a result of this proof, we find a bijection between binary de Bruijn sequences of degree n and binary sequences of length 2n−1. Finally, we determine the critical groups of all the Kautz graphs and de Bruijn graphs, generalizing a result of Levine [7].

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 20 , Issue 1 , January 2011 , pp. 11 - 25
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Berget, A., Manion, A., Maxwell, M., Potechin, A. and Reiner, V. The critical group of a line graph. arXiv:0904.1246.Google Scholar
[2]Biggs, N. L. (1999) Chip-firing and the critical group of a graph. J. Algebraic Combin. 9 25–45.CrossRefGoogle Scholar
[3]Christianson, H. and Reiner, V. (2002) The critical group of a threshold graph. Linear Algebra Appl. 349 233–244.CrossRefGoogle Scholar
[4]Holroyd, A. E., Levine, L., Mészáros, K., Peres, Y., Propp, J. and Wilson, D. B. (2008) Chip-firing and rotor-routing on directed graphs. In In and Out of Equilibrium 2, Vol. 60 of Progress in Probability, Birkhäuser, pp. 331–364.CrossRefGoogle Scholar
[5]Jacobson, B., Niedermaier, A. and Reiner, V. (2003) Critical groups for complete multipartite graphs and Cartesian products of complete graphs. J. Graph Theory 44 231–250.CrossRefGoogle Scholar
[6]Knuth, D. E. (1967) Oriented subtrees of an arc digraph. J. Combin. Theory 3 309–314.CrossRefGoogle Scholar
[7]Levine, L. (2010) Sandpile groups and spanning trees of directed line graphs. To appear in Journal of Combinatorial Theory, Series A. arXiv:0906.2809.Google Scholar
[8]Stanley, R. P. (1999) Enumerative Combinatorics, Vol. 1, Cambridge University Press.CrossRefGoogle Scholar