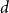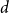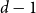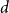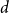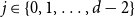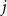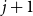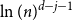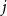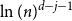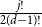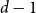1. Introduction
There are numerous models that generate different types of sparse random graphs. Among them is the
![]() $d$
-process, defined in the following way: start with
$d$
-process, defined in the following way: start with
![]() $n$
vertices and 0 edges, and at each time step, choose a pair
$n$
vertices and 0 edges, and at each time step, choose a pair
![]() $\{u,v\}$
uniformly at random over all pairs consisting of vertices which have degree less than
$\{u,v\}$
uniformly at random over all pairs consisting of vertices which have degree less than
![]() $d$
and are not joined to each other by an edge.
$d$
and are not joined to each other by an edge.
![]() $d$
could be allowed to change with
$d$
could be allowed to change with
![]() $n$
, but for the rest of this paper
$n$
, but for the rest of this paper
![]() $d$
is always a fixed constant (this is also assumed in all relevant citations). Ruciński and Wormald showed that with high probability, abbreviated “w.h.p.” (i.e. with probability converging to 1 as
$d$
is always a fixed constant (this is also assumed in all relevant citations). Ruciński and Wormald showed that with high probability, abbreviated “w.h.p.” (i.e. with probability converging to 1 as
![]() $n \to \infty$
) the
$n \to \infty$
) the
![]() $d$
-process ends with
$d$
-process ends with
![]() $\lfloor dn/2 \rfloor$
edges [Reference Ruciński and Wormald11]. There is still much that is unknown about the
$\lfloor dn/2 \rfloor$
edges [Reference Ruciński and Wormald11]. There is still much that is unknown about the
![]() $d$
-process; for example, it is not known whether the
$d$
-process; for example, it is not known whether the
![]() $d$
-process is contiguous with the
$d$
-process is contiguous with the
![]() $d$
-uniform random graph model for any
$d$
-uniform random graph model for any
![]() $d \geq 2$
; i.e. if any event that happens with high probability in one happens with high probability in the other. A recent paper by Molloy, Surya, and Warnke [Reference Molloy, Surya and Warnke8] disproves this relation if there is enough “non-uniformity” of the vertex degrees (with an appropriate modification of the
$d \geq 2$
; i.e. if any event that happens with high probability in one happens with high probability in the other. A recent paper by Molloy, Surya, and Warnke [Reference Molloy, Surya and Warnke8] disproves this relation if there is enough “non-uniformity” of the vertex degrees (with an appropriate modification of the
![]() $d$
-process for non-regular graphs); it also contains a good history of the
$d$
-process for non-regular graphs); it also contains a good history of the
![]() $d$
-process. See ref. [Reference Janson, Ruciński and Luczak7, Section 9.6] for more on contiguity.
$d$
-process. See ref. [Reference Janson, Ruciński and Luczak7, Section 9.6] for more on contiguity.
A couple of notable results have been given for the case where
![]() $d = 2$
: the expected numbers of cycles of constant sizes were studied by Ruciński and Wormald in ref. [Reference Ruciński and Wormald10], and in ref. [Reference Telcs, Wormald and Zhou13], Telcs, Wormald, and Zhou calculated the probability that the 2-process ends with a Hamiltonian cycle. In these works, the authors establish estimates on certain graph parameters, such as the number of vertices of a certain degree, that hold throughout the process. This is done with the so-called “differential equations method” for random graph processes, which uses martingale inequalities to give variable bounds; in ref. [Reference Wormald14] Wormald gives a thorough description of this method.
$d = 2$
: the expected numbers of cycles of constant sizes were studied by Ruciński and Wormald in ref. [Reference Ruciński and Wormald10], and in ref. [Reference Telcs, Wormald and Zhou13], Telcs, Wormald, and Zhou calculated the probability that the 2-process ends with a Hamiltonian cycle. In these works, the authors establish estimates on certain graph parameters, such as the number of vertices of a certain degree, that hold throughout the process. This is done with the so-called “differential equations method” for random graph processes, which uses martingale inequalities to give variable bounds; in ref. [Reference Wormald14] Wormald gives a thorough description of this method.
More recently, Ruciński and Wormald announced a new analysis of the
![]() $d$
-process that hinges on a coupling with a balls-in-bins process. This simple argument gives a precise estimate of the probability that the
$d$
-process that hinges on a coupling with a balls-in-bins process. This simple argument gives a precise estimate of the probability that the
![]() $d$
-process ends with
$d$
-process ends with
![]() $\lfloor dn/2 \rfloor$
edges (i.e. the probability that the
$\lfloor dn/2 \rfloor$
edges (i.e. the probability that the
![]() $d$
-process reaches saturation). This argument includes estimaes for the number of vertices of each degree near the end of the process. This work was presented by Ruciński at the 2023 Random Structures and Algorithms conference. Ruciński’s presentation included the following problem (which was open at the time): when do we expect the last vertex of degree
$d$
-process reaches saturation). This argument includes estimaes for the number of vertices of each degree near the end of the process. This work was presented by Ruciński at the 2023 Random Structures and Algorithms conference. Ruciński’s presentation included the following problem (which was open at the time): when do we expect the last vertex of degree
![]() $j$
(for any
$j$
(for any
![]() $j$
from 0 to
$j$
from 0 to
![]() $d-2$
) to disappear? The question was also stated earlier for
$d-2$
) to disappear? The question was also stated earlier for
![]() $d=2$
and
$d=2$
and
![]() $j=0$
by Ruciński and Wormald [Reference Ruciński and Wormald10, Question 3]. In November of 2023, after the first release of the pre-print of this paper, Ruciński and Wormald released a pre-print of their balls-and-bins argument which also included an answer to Ruciński’s question [Reference Ruciński and Wormald12]. Our main result uses the differential equations method (as described in the previous paragraph) and gives a slightly stronger answer:
$j=0$
by Ruciński and Wormald [Reference Ruciński and Wormald10, Question 3]. In November of 2023, after the first release of the pre-print of this paper, Ruciński and Wormald released a pre-print of their balls-and-bins argument which also included an answer to Ruciński’s question [Reference Ruciński and Wormald12]. Our main result uses the differential equations method (as described in the previous paragraph) and gives a slightly stronger answer:
Theorem 1.
Consider the d-process on a vertex set of size n, and for each
![]() $\ell \in \{0\} \cup [d-2]$
, let the random variable
$\ell \in \{0\} \cup [d-2]$
, let the random variable
![]() $T_{\ell }$
be the step at which the number of vertices of degree at most
$T_{\ell }$
be the step at which the number of vertices of degree at most
![]() $\ell$
becomes 0. Then the sequence (over
$\ell$
becomes 0. Then the sequence (over
![]() $n$
) of random
$n$
) of random
![]() $d-1$
-tuples consisting of the variables
$d-1$
-tuples consisting of the variables
converges in distribution to the product of
![]() $d-1$
independent exponential random variables of mean 1.
$d-1$
independent exponential random variables of mean 1.
In this paper we use the differential equations method with increasingly precise estimates of certain random variables; these estimates are known as self-correcting. Previous results that use self-correcting estimates include [Reference Telcs, Wormald and Zhou13], [Reference Bohman and Picollelli6], [Reference Bohman, Frieze and Lubetzky3], [Reference Bohman, Frieze and Lubetzky4], [Reference Bohman and Keevash5], and [Reference Pontiveros, Griffiths and Morris9]. There have been various approaches to achieving self-correcting estimates; the approach in this paper uses critical intervals, regions of possible values of a random variable in which we expect subsequent variables to increase/decrease over time. Critical intervals used in this fashion first appeared in a result of Bohman and Picollelli [Reference Bohman and Picollelli6]. For an introduction to and discussion of the method see Bohman, Frieze, and Lubetzky [Reference Bohman, Frieze and Lubetzky3].
The proof of Theorem 1 is divided into four sections. In Section 2, we introduce random variables of the form
![]() $S^{(j)}_i$
which count the number of vertices of degree at most
$S^{(j)}_i$
which count the number of vertices of degree at most
![]() $j$
after
$j$
after
![]() $i$
steps, define approximating functions
$i$
steps, define approximating functions
![]() $s_{j}(t)$
with the eventual goal of showing that
$s_{j}(t)$
with the eventual goal of showing that
![]() $S^{(j)}_{i} \approx ns_{j}(i/n)$
for most of the process, and derive useful properties of these functions. One such property is that, when there are at most
$S^{(j)}_{i} \approx ns_{j}(i/n)$
for most of the process, and derive useful properties of these functions. One such property is that, when there are at most
![]() $n^{c}$
steps left for some constant
$n^{c}$
steps left for some constant
![]() $c \lt 1$
,
$c \lt 1$
,
for each
![]() $j$
; this hierarchy of functions helps us to focus on each variable
$j$
; this hierarchy of functions helps us to focus on each variable
![]() $S^{(j)}_i$
independently of the others when it is near 0, which motivates the form of the limiting exponential random variables in Theorem 1. At the end of Section 2 we introduce two martingale inequalities used by Bohman [Reference Bohman2] and make a slight modification to them to use later in the paper. In Section 3, we work with a more ‘standard martingale method’ (without the use of critical intervals) to show that
$S^{(j)}_i$
independently of the others when it is near 0, which motivates the form of the limiting exponential random variables in Theorem 1. At the end of Section 2 we introduce two martingale inequalities used by Bohman [Reference Bohman2] and make a slight modification to them to use later in the paper. In Section 3, we work with a more ‘standard martingale method’ (without the use of critical intervals) to show that
![]() $S^{(j)}_{i} \approx ns_{j}(i/n)$
until there are
$S^{(j)}_{i} \approx ns_{j}(i/n)$
until there are
![]() $n^{1 - 1/(100d)}$
steps left. Here we allow the error bounds to increase over time. In Section 4, we use a more refined martingale method (including the use of critical intervals) to show that
$n^{1 - 1/(100d)}$
steps left. Here we allow the error bounds to increase over time. In Section 4, we use a more refined martingale method (including the use of critical intervals) to show that
![]() $S^{(j)}_{i} \approx ns_{j}(i/n)$
continues to hold until there are
$S^{(j)}_{i} \approx ns_{j}(i/n)$
continues to hold until there are
![]() $\ln (n) ^{d-0.8-j}$
steps left; here the error bounds decrease over time, and so are self-correcting. In Section 5, we complete the proof of Theorem 1 by using a pairing argument to show that, in the last steps of the
$\ln (n) ^{d-0.8-j}$
steps left; here the error bounds decrease over time, and so are self-correcting. In Section 5, we complete the proof of Theorem 1 by using a pairing argument to show that, in the last steps of the
![]() $d$
-process, the behaviour of the random variable in question can be well-approximated by a certain uniform distribution of time steps. Sections 4 and 5 are both parts of a proof by induction over a series of intervals of time steps, though we give each part its own section as the methods used in each are very different.
$d$
-process, the behaviour of the random variable in question can be well-approximated by a certain uniform distribution of time steps. Sections 4 and 5 are both parts of a proof by induction over a series of intervals of time steps, though we give each part its own section as the methods used in each are very different.
2. Preliminaries
First, two technical notes: we use the standard notation of symbols
![]() $o, O, \Theta, \omega, \Omega, \ll, \gg$
, and
$o, O, \Theta, \omega, \Omega, \ll, \gg$
, and
![]() $\sim$
to compare functions asymptotically (e.g. see pages 9-10 of [Reference Janson, Ruciński and Luczak7]). We also note that, throughout the paper, we assume
$\sim$
to compare functions asymptotically (e.g. see pages 9-10 of [Reference Janson, Ruciński and Luczak7]). We also note that, throughout the paper, we assume
![]() $n$
to be arbitrarily large.
$n$
to be arbitrarily large.
In this section we set up sequences of random variables, describe how the evolution of the
![]() $d$
-process depends on these, and deduce properties of certain approximating functions; such functions are used to estimate the number of vertices of given degrees throughout the process (much of this is also described in ref. [Reference Telcs, Wormald and Zhou13] with similar notation; the one major difference is that we use
$d$
-process depends on these, and deduce properties of certain approximating functions; such functions are used to estimate the number of vertices of given degrees throughout the process (much of this is also described in ref. [Reference Telcs, Wormald and Zhou13] with similar notation; the one major difference is that we use
![]() $i$
instead of
$i$
instead of
![]() $t$
for the number of time steps, and
$t$
for the number of time steps, and
![]() $t$
instead of
$t$
instead of
![]() $x$
for the corresponding time variable). Consider a sequence of graphs
$x$
for the corresponding time variable). Consider a sequence of graphs
![]() $G_0,G_1,\dots,G_{\lfloor dn/2 \rfloor }$
, where
$G_0,G_1,\dots,G_{\lfloor dn/2 \rfloor }$
, where
![]() $G_0$
is the empty graph of
$G_0$
is the empty graph of
![]() $n$
vertices, and for
$n$
vertices, and for
![]() $i \in [n]$
, let
$i \in [n]$
, let
![]() $G_i$
be formed by adding an edge uniformly at random to
$G_i$
be formed by adding an edge uniformly at random to
![]() $G_{i-1}$
so that the maximum degree of
$G_{i-1}$
so that the maximum degree of
![]() $G_i$
is at most
$G_i$
is at most
![]() $d$
(in the unlikely event that there are no valid edges to add after
$d$
(in the unlikely event that there are no valid edges to add after
![]() $s$
steps for some
$s$
steps for some
![]() $s \lt \lfloor dn/2 \rfloor$
, let
$s \lt \lfloor dn/2 \rfloor$
, let
![]() $G_i = G_{s}$
for all
$G_i = G_{s}$
for all
![]() $i \gt s$
). Next, we define several sequences of random variables: For all
$i \gt s$
). Next, we define several sequences of random variables: For all
![]() $i, j, j_1, j_2$
such that
$i, j, j_1, j_2$
such that
![]() $0 \leq i \leq \lfloor \frac{dn}{2} \rfloor$
,
$0 \leq i \leq \lfloor \frac{dn}{2} \rfloor$
,
![]() $0 \leq j \leq d$
, and
$0 \leq j \leq d$
, and
![]() $0 \leq j_1 \leq j_2 \leq d-1$
, define:
$0 \leq j_1 \leq j_2 \leq d-1$
, define:
![]() $Y^{(j)}_i \,:\!=\,$
the number of vertices in
$Y^{(j)}_i \,:\!=\,$
the number of vertices in
![]() $G_i$
with degree
$G_i$
with degree
![]() $j$
$j$
![]() $S^{(j)}_i \,:\!=\,$
the number of vertices in
$S^{(j)}_i \,:\!=\,$
the number of vertices in
![]() $G_i$
with degree at most
$G_i$
with degree at most
![]() $j$
$j$
![]() $Z^{(j_1,j_2)}_i \,:\!=\,$
the number of edges
$Z^{(j_1,j_2)}_i \,:\!=\,$
the number of edges
![]() $\{v_1,v_2\}$
in
$\{v_1,v_2\}$
in
![]() $G_i$
for which
$G_i$
for which
![]() $Z_i \,:\!=\, \displaystyle \sum _{0 \leq j_1 \leq j_2 \leq d-1} Z^{(j_1,j_2)}_i$
.
$Z_i \,:\!=\, \displaystyle \sum _{0 \leq j_1 \leq j_2 \leq d-1} Z^{(j_1,j_2)}_i$
.
By definition and by edge-counting we have
 \begin{equation*}\sum _{j=0}^{d} Y_i^{(j)} = n \qquad \text {and} \qquad \sum _{j=1}^{d} j Y_i^{(j)} = 2i.\end{equation*}
\begin{equation*}\sum _{j=0}^{d} Y_i^{(j)} = n \qquad \text {and} \qquad \sum _{j=1}^{d} j Y_i^{(j)} = 2i.\end{equation*}
Combining the equations above gives us
 \begin{equation} \sum _{j=0}^{d-1} S_i^{(j)} = \sum _{j=0}^{d-1} (d-j) Y_i^{(j)} = dn-2i. \end{equation}
\begin{equation} \sum _{j=0}^{d-1} S_i^{(j)} = \sum _{j=0}^{d-1} (d-j) Y_i^{(j)} = dn-2i. \end{equation}
One can also quickly verify from (1) and by definition of
![]() $S^{(d-1)}_i$
,
$S^{(d-1)}_i$
,
![]() $Z^{(j_1,j_2)}_{i}$
, and
$Z^{(j_1,j_2)}_{i}$
, and
![]() $Z_i$
, that
$Z_i$
, that
Throughout the process we will keep track of the variables
![]() $S^{(j)}$
using martingale arguments. This is sufficient for us, as the
$S^{(j)}$
using martingale arguments. This is sufficient for us, as the
![]() $Y$
variables can be derived from the
$Y$
variables can be derived from the
![]() $S$
variables, and because none of the
$S$
variables, and because none of the
![]() $Z$
variables will have any significant effect in any of our calculations, as we will see later.
$Z$
variables will have any significant effect in any of our calculations, as we will see later.
Our next step is to estimate the expected on-step change of
![]() $S^{(j)}_i$
, known as the “trend hypothesis” in ref. [Reference Wormald14]. Note that
$S^{(j)}_i$
, known as the “trend hypothesis” in ref. [Reference Wormald14]. Note that
![]() $S^{(j)}_{i} - S^{(j)}_{i+1}$
equals the number of vertices of degree
$S^{(j)}_{i} - S^{(j)}_{i+1}$
equals the number of vertices of degree
![]() $j$
that are picked at the
$j$
that are picked at the
![]() $i+1$
time step; hence, for all
$i+1$
time step; hence, for all
![]() $j \in \{0\} \cup [d-1]$
:
$j \in \{0\} \cup [d-1]$
:
 \begin{align} \mathbb{E}\left[S^{(j)}_{i+1} - S^{(j)}_{i} \mid G_i\right] &= \frac{-Y^{(j)}_i \left(S^{(d-1)}_i - 1\right) + \displaystyle \sum _{k \leq j} Z^{(k,j)}_i + \sum _{k \geq j} Z^{(j,k)}_i }{\binom{S^{(d-1)}_i}{2} - Z_i} \nonumber \\&= \frac{-2Y^{(j)}_i}{S^{(d-1)}_i}\left (1 + O\left (\frac{1}{dn-2i}\right )\right ) \qquad \text{by (2)} \end{align}
\begin{align} \mathbb{E}\left[S^{(j)}_{i+1} - S^{(j)}_{i} \mid G_i\right] &= \frac{-Y^{(j)}_i \left(S^{(d-1)}_i - 1\right) + \displaystyle \sum _{k \leq j} Z^{(k,j)}_i + \sum _{k \geq j} Z^{(j,k)}_i }{\binom{S^{(d-1)}_i}{2} - Z_i} \nonumber \\&= \frac{-2Y^{(j)}_i}{S^{(d-1)}_i}\left (1 + O\left (\frac{1}{dn-2i}\right )\right ) \qquad \text{by (2)} \end{align}
 \begin{align} &= \frac{-2 Y^{(j)}_i}{S^{(d-1)}_i}+ O\left (\frac{1}{dn-2i}\right ). \end{align}
\begin{align} &= \frac{-2 Y^{(j)}_i}{S^{(d-1)}_i}+ O\left (\frac{1}{dn-2i}\right ). \end{align}
For
![]() $j \in \{0\} \cup [d-1]$
we define approximating functions
$j \in \{0\} \cup [d-1]$
we define approximating functions
![]() $y_j:[0,d/2) \to{\mathbb{R}}$
and
$y_j:[0,d/2) \to{\mathbb{R}}$
and
![]() $s_j:[0,d/2) \to{\mathbb{R}}$
: let
$s_j:[0,d/2) \to{\mathbb{R}}$
: let
![]() $y_j(t)$
,
$y_j(t)$
,
![]() $s_j(t)$
be functions such that
$s_j(t)$
be functions such that
![]() $s_j = \sum _{k=0}^{j} y_k$
,
$s_j = \sum _{k=0}^{j} y_k$
,
![]() $y_0(0) = 1$
and
$y_0(0) = 1$
and
![]() $y_k(0) = 0$
for all
$y_k(0) = 0$
for all
![]() $k \in [d-1]$
(equivalent to
$k \in [d-1]$
(equivalent to
![]() $s_j(0) = 1$
for all
$s_j(0) = 1$
for all
![]() $j$
), and (assuming the “dummy functions”
$j$
), and (assuming the “dummy functions”
![]() $y_{-1}(t) = s_{-1}(t) = 0$
):
$y_{-1}(t) = s_{-1}(t) = 0$
):
By (5) and the chain rule, for all
![]() $j \in [d-1]$
:
$j \in [d-1]$
:
Since the above equation is first-order linear, we have, for some constant
![]() $C_j$
:
$C_j$
:
 \begin{equation*}y_j = y_0\left ({-}\int \frac {y_{j-1}}{y_0^2} d y_0 + C_j\right ).\end{equation*}
\begin{equation*}y_j = y_0\left ({-}\int \frac {y_{j-1}}{y_0^2} d y_0 + C_j\right ).\end{equation*}
Using the above recursively with initial conditions, we have, for all
![]() $j \in [d-1]$
:
$j \in [d-1]$
:
To solve for an explicit formula relating
![]() $y_0$
and
$y_0$
and
![]() $t$
, note that, by (5):
$t$
, note that, by (5):
 \begin{equation*}\frac {d}{dt} \left ( \sum _{j=0}^{d-1} (d-j) y_j \right )= \frac {-2 \displaystyle \sum _{j=0}^{d-1}y_j}{s_{d-1}} = -2,\end{equation*}
\begin{equation*}\frac {d}{dt} \left ( \sum _{j=0}^{d-1} (d-j) y_j \right )= \frac {-2 \displaystyle \sum _{j=0}^{d-1}y_j}{s_{d-1}} = -2,\end{equation*}
hence, using initial conditions (note the resemblance to (1)):
 \begin{equation} \sum _{j=0}^{d-1} s_j = \sum _{j=0}^{d-1} (d-j) y_j = d - 2t. \end{equation}
\begin{equation} \sum _{j=0}^{d-1} s_j = \sum _{j=0}^{d-1} (d-j) y_j = d - 2t. \end{equation}
Equations (6) and (7) together give us a complete description of the functions
![]() $y_j$
and
$y_j$
and
![]() $s_j$
. We will now prove some useful properties of these functions. To start, we can combine (6) and (7) to get
$s_j$
. We will now prove some useful properties of these functions. To start, we can combine (6) and (7) to get
 \begin{equation} \sum _{j=0}^{d-1} \frac{y_0 ({-}\ln (y_0))^j (d-j)}{j!} = d - 2t. \end{equation}
\begin{equation} \sum _{j=0}^{d-1} \frac{y_0 ({-}\ln (y_0))^j (d-j)}{j!} = d - 2t. \end{equation}
Note that, by continuity of
![]() $y_0$
and by (8),
$y_0$
and by (8),
![]() $y_0 \gt 0$
over its domain. Next, by summing up (6) over
$y_0 \gt 0$
over its domain. Next, by summing up (6) over
![]() $j \in \{0\} \cup [d-1]$
((6) holds for
$j \in \{0\} \cup [d-1]$
((6) holds for
![]() $j=0$
also) one can see that
$j=0$
also) one can see that
![]() $s_{d-1}$
is positive if
$s_{d-1}$
is positive if
![]() $y_0 \leq 1$
. This, combined with
$y_0 \leq 1$
. This, combined with
![]() $\frac{d y_0}{dt} = \frac{-2y_0}{s_{d-1}}$
, tells us that
$\frac{d y_0}{dt} = \frac{-2y_0}{s_{d-1}}$
, tells us that
![]() $y_0$
is decreasing and
$y_0$
is decreasing and
![]() $s_{d-1}$
is positive. It follows from
$s_{d-1}$
is positive. It follows from
![]() $y_0 \in (0,1]$
and (6) that each
$y_0 \in (0,1]$
and (6) that each
![]() $y_j$
is positive for
$y_j$
is positive for
![]() $t \not = 0$
. In turn, this implies that
$t \not = 0$
. In turn, this implies that
![]() $0 \leq y_j \leq s_j \leq s_{d-1}$
for each
$0 \leq y_j \leq s_j \leq s_{d-1}$
for each
![]() $j$
. From this it follows that
$j$
. From this it follows that
![]() $ds_{d-1}$
is at least the left expression of (7), so
$ds_{d-1}$
is at least the left expression of (7), so
![]() $s_{d-1} \geq 1 - \frac{2t}{d}$
. We make a special note of the last couple of properties mentioned:
$s_{d-1} \geq 1 - \frac{2t}{d}$
. We make a special note of the last couple of properties mentioned:
Next, we want to understand the behaviour of each function when
![]() $t$
is close to
$t$
is close to
![]() $\frac{d}{2}$
, as this is the most critical point of the process. Consider (8) again. As
$\frac{d}{2}$
, as this is the most critical point of the process. Consider (8) again. As
![]() $t \to \frac{d}{2}, y_0 \to 0$
, so
$t \to \frac{d}{2}, y_0 \to 0$
, so
![]() $\frac{y_0({-} \ln (y_0))^{d-1}}{(d-1)!}$
will be the most dominant term on the left; hence,
$\frac{y_0({-} \ln (y_0))^{d-1}}{(d-1)!}$
will be the most dominant term on the left; hence,
This, combined with (6) gives us, for all
![]() $j \in \{0 \} \cup [d-1]$
:
$j \in \{0 \} \cup [d-1]$
:
For large enough
![]() $t$
(and hence, for a large enough step
$t$
(and hence, for a large enough step
![]() $i$
), we can approximate the above expression:
$i$
), we can approximate the above expression:
One can now see that, near the end of the process,
![]() $s_j/s_{j-1} = \Theta (\ln (n))$
, as mentioned in the introduction.
$s_j/s_{j-1} = \Theta (\ln (n))$
, as mentioned in the introduction.
Finally, we introduce two martingale inequalities from a result of Bohman [Reference Bohman2] which will be used in Section 4 in a slightly modified form. The original inequalities are as follows:
Lemma 2 (Lemma 6 from [Reference Bohman2]). Suppose
![]() $a, \eta,$
and
$a, \eta,$
and
![]() $N$
are positive,
$N$
are positive,
![]() $\eta \leq N/2$
, and
$\eta \leq N/2$
, and
![]() $a \lt \eta m$
. If
$a \lt \eta m$
. If
![]() $0 = A_0, A_1,\dots, A_m$
is a submartingale such that
$0 = A_0, A_1,\dots, A_m$
is a submartingale such that
![]() $-\eta \leq A_{i+1} - A_{i} \leq N$
for all
$-\eta \leq A_{i+1} - A_{i} \leq N$
for all
![]() $i$
, then
$i$
, then
Lemma 3 (Lemma 7 from [Reference Bohman2]). Suppose
![]() $a, \eta,$
and
$a, \eta,$
and
![]() $N$
are positive,
$N$
are positive,
![]() $\eta \leq N/10$
, and
$\eta \leq N/10$
, and
![]() $a \lt \eta m$
. If
$a \lt \eta m$
. If
![]() $0 = A_0, A_1,\dots, A_m$
is a supermartingale such that
$0 = A_0, A_1,\dots, A_m$
is a supermartingale such that
![]() $-\eta \leq A_{i+1} - A_{i} \leq N$
for all
$-\eta \leq A_{i+1} - A_{i} \leq N$
for all
![]() $i$
, then
$i$
, then
We present the following modification, which removes the requirement
![]() $a \lt \eta m$
and modifies one of the inequalities slightly:
$a \lt \eta m$
and modifies one of the inequalities slightly:
Corollary 4.
Suppose
![]() $a, \eta,$
and
$a, \eta,$
and
![]() $N$
are positive, and
$N$
are positive, and
![]() $\eta \leq N/2$
. If
$\eta \leq N/2$
. If
![]() $0 = A_0, A_1,\dots, A_m$
is a submartingale such that
$0 = A_0, A_1,\dots, A_m$
is a submartingale such that
![]() $-\eta \leq A_{i+1} - A_{i} \leq N$
for all
$-\eta \leq A_{i+1} - A_{i} \leq N$
for all
![]() $i$
, then
$i$
, then
Corollary 5.
Suppose
![]() $a, \eta,$
and
$a, \eta,$
and
![]() $N$
are positive, and
$N$
are positive, and
![]() $\eta \leq N/10$
. If
$\eta \leq N/10$
. If
![]() $0 = A_0, A_1,\dots, A_m$
is a supermartingale such that
$0 = A_0, A_1,\dots, A_m$
is a supermartingale such that
![]() $-\eta \leq A_{i+1} - A_{i} \leq N$
for all
$-\eta \leq A_{i+1} - A_{i} \leq N$
for all
![]() $i$
, then
$i$
, then
Corollary 4 is nearly immediate from Lemma 2: first, one can extend the result to include
![]() $a = \eta m$
by using left-continuity (with respect to
$a = \eta m$
by using left-continuity (with respect to
![]() $a$
) of both sides of the inequality; we hence assume
$a$
) of both sides of the inequality; we hence assume
![]() $a \gt \eta m$
. Since
$a \gt \eta m$
. Since
![]() $A_{i+1} - A_i \geq -\eta \gt -a/m$
, then
$A_{i+1} - A_i \geq -\eta \gt -a/m$
, then
![]() $A_m = A_m - A_0 \gt -a$
. We now derive Corollary 5 from Lemma 3: assume
$A_m = A_m - A_0 \gt -a$
. We now derive Corollary 5 from Lemma 3: assume
![]() $a \geq \eta m$
, and let
$a \geq \eta m$
, and let
![]() $m^{\prime} \in \mathbb{Z}^+$
such that
$m^{\prime} \in \mathbb{Z}^+$
such that
![]() $a \lt \eta m^{\prime} \leq 2a$
. Extend the martingale by adding variables
$a \lt \eta m^{\prime} \leq 2a$
. Extend the martingale by adding variables
![]() $A_{m+1},\dots,A_{m^{\prime}}$
which are all equal to
$A_{m+1},\dots,A_{m^{\prime}}$
which are all equal to
![]() $A_m$
. Apply Lemma 3 with
$A_m$
. Apply Lemma 3 with
![]() $m$
replaced with
$m$
replaced with
![]() $m^{\prime}$
, and use
$m^{\prime}$
, and use
![]() $\eta m^{\prime} \leq 2a$
to get
$\eta m^{\prime} \leq 2a$
to get
Combining the case
![]() $a \lt \eta m$
from Lemma 3 and the case
$a \lt \eta m$
from Lemma 3 and the case
![]() $a \geq \eta m$
above gives Corollary 5.
$a \geq \eta m$
above gives Corollary 5.
3. First phase
Let
![]() $i_{trans} = \lfloor \frac{dn}{2} - n^{1 - 1/(100d)} \rfloor$
. The objective of this section is to prove the following Theorem:
$i_{trans} = \lfloor \frac{dn}{2} - n^{1 - 1/(100d)} \rfloor$
. The objective of this section is to prove the following Theorem:
Theorem 6.
Define
![]() $E_{first}(i) \,:\!=\, n^{0.6} \left (\frac{dn}{dn-2i}\right )^{4d}$
. With high probability, for all
$E_{first}(i) \,:\!=\, n^{0.6} \left (\frac{dn}{dn-2i}\right )^{4d}$
. With high probability, for all
![]() $i \leq i_{trans}$
and all
$i \leq i_{trans}$
and all
![]() $j \in \{ 0 \} \cup [d-1]$
:
$j \in \{ 0 \} \cup [d-1]$
:
Now we define two new random variables for each
![]() $j$
:
$j$
:
 \begin{align*} S^{(j)+}_{i} &\,:\!=\, S^{(j)}_i - n s_j(i/n) - E_{first}(i)\\ S^{(j)-}_{i} &\,:\!=\, S^{(j)}_i - n s_j(i/n) + E_{first}(i). \end{align*}
\begin{align*} S^{(j)+}_{i} &\,:\!=\, S^{(j)}_i - n s_j(i/n) - E_{first}(i)\\ S^{(j)-}_{i} &\,:\!=\, S^{(j)}_i - n s_j(i/n) + E_{first}(i). \end{align*}
Next, we introduce a stopping time
![]() $T$
, defined as the first step
$T$
, defined as the first step
![]() $i \leq i_{trans}$
for which (12) is not satisfied for some
$i \leq i_{trans}$
for which (12) is not satisfied for some
![]() $j$
; if (12) always holds, then let
$j$
; if (12) always holds, then let
![]() $T = \infty$
. Although this stopping time is not necessarily needed to prove Theorem 6, it does make some calculations easier, and moreover, a similar stopping time will be necessary for the following section; hence, this serves as a good warm-up. Let variable name
$T = \infty$
. Although this stopping time is not necessarily needed to prove Theorem 6, it does make some calculations easier, and moreover, a similar stopping time will be necessary for the following section; hence, this serves as a good warm-up. Let variable name
![]() $W$
be introduced to equip this stopping time to variable
$W$
be introduced to equip this stopping time to variable
![]() $S$
, i.e.
$S$
, i.e.
 \begin{align*} &W^{(j)+}_{i} \,:\!=\, \begin{cases} S^{(j)+}_{i}, i \lt T \\[5pt] S^{(j)+}_{T}, i \geq T \end{cases} \quad W^{(j)-}_i \,:\!=\, \begin{cases} S^{(j)-}_i, i \lt T \\[5pt] S^{(j)-}_T, i \geq T. \end{cases} \end{align*}
\begin{align*} &W^{(j)+}_{i} \,:\!=\, \begin{cases} S^{(j)+}_{i}, i \lt T \\[5pt] S^{(j)+}_{T}, i \geq T \end{cases} \quad W^{(j)-}_i \,:\!=\, \begin{cases} S^{(j)-}_i, i \lt T \\[5pt] S^{(j)-}_T, i \geq T. \end{cases} \end{align*}
Note that
![]() $W^{(j)+}_{i}$
corresponds to the upper boundary and
$W^{(j)+}_{i}$
corresponds to the upper boundary and
![]() $W^{(j)-}_i$
to the lower one in the sense that crossing the corresponding boundary will make the corresponding variable change signs; furthermore, the inequality of Theorem 6 holds if and only if
$W^{(j)-}_i$
to the lower one in the sense that crossing the corresponding boundary will make the corresponding variable change signs; furthermore, the inequality of Theorem 6 holds if and only if
![]() $W^{(j)+}_{i_{trans}} \leq 0$
and
$W^{(j)+}_{i_{trans}} \leq 0$
and
![]() $W^{(j)-}_{i_{trans}} \geq 0$
for each
$W^{(j)-}_{i_{trans}} \geq 0$
for each
![]() $j$
. We now state our martingale Lemma:
$j$
. We now state our martingale Lemma:
Lemma 7.
Restricted to
![]() $i \leq i_{trans}$
, for all
$i \leq i_{trans}$
, for all
![]() $j, \ \big(W^{(j)-}_{i}\big)_i$
is a submartingale and
$j, \ \big(W^{(j)-}_{i}\big)_i$
is a submartingale and
![]() $\big(W^{(j)+}_{i}\big)_i$
is a supermartingale.
$\big(W^{(j)+}_{i}\big)_i$
is a supermartingale.
Proof. Here we just prove the first part of the Lemma; the second part follows from nearly identical calculations. Fix some arbitrary
![]() $i \leq i_{trans}$
; we need to show that
$i \leq i_{trans}$
; we need to show that
Also assume that
![]() $T \geq i+1$
, else
$T \geq i+1$
, else
![]() $W^{(j)-}_{i+1} - W^{(j)-}_i = 0$
and we are done; it follows that
$W^{(j)-}_{i+1} - W^{(j)-}_i = 0$
and we are done; it follows that
![]() $W^{(j)-}_i = S^{(j)-}_i, W^{(j)-}_{i+1} = S^{(j)-}_{i+1}$
, and (12) holds for the fixed
$W^{(j)-}_i = S^{(j)-}_i, W^{(j)-}_{i+1} = S^{(j)-}_{i+1}$
, and (12) holds for the fixed
![]() $i$
. By (4) and (5) and using Taylor’s Theorem, we have, for some
$i$
. By (4) and (5) and using Taylor’s Theorem, we have, for some
![]() $\psi \in [i,i+1]$
:
$\psi \in [i,i+1]$
:
 \begin{align*} \mathbb{E}\left[S^{(j)-}_{i+1} - S^{(j)-}_i \mid G_i\right] &= \frac{-2 Y^{(j)}_i}{S^{(d-1)}_i} + O\left (\frac{1}{dn-2i}\right ) + \frac{2y_j(i/n)}{s_{d-1}(i/n)} -\frac{d^2}{d\mu ^2}\left (\frac{ns_j(\mu/n)}{2}\right )\Big |_{\mu = \psi } \\[5pt]& \quad + \left(E_{first}(i+1) - E_{first}(i)\right). \end{align*}
\begin{align*} \mathbb{E}\left[S^{(j)-}_{i+1} - S^{(j)-}_i \mid G_i\right] &= \frac{-2 Y^{(j)}_i}{S^{(d-1)}_i} + O\left (\frac{1}{dn-2i}\right ) + \frac{2y_j(i/n)}{s_{d-1}(i/n)} -\frac{d^2}{d\mu ^2}\left (\frac{ns_j(\mu/n)}{2}\right )\Big |_{\mu = \psi } \\[5pt]& \quad + \left(E_{first}(i+1) - E_{first}(i)\right). \end{align*}
We split the above expression
![]() $\Big($
excluding
$\Big($
excluding
![]() $O\left (\frac{1}{dn-2i}\right )\Big)$
into three summands.
$O\left (\frac{1}{dn-2i}\right )\Big)$
into three summands.
-
1. Here we make use of the fact that
 $Y^{(j)}_i = S^{(j)}_i - S^{(j-1)}_{i}$
and
$Y^{(j)}_i = S^{(j)}_i - S^{(j-1)}_{i}$
and
 $y_j(t) = s_j(t) - s_{j-1}(t)$
. We have (putting
$y_j(t) = s_j(t) - s_{j-1}(t)$
. We have (putting
 $s_{j-1}$
and
$s_{j-1}$
and
 $S_i^{({-}1)} = 0$
):
$S_i^{({-}1)} = 0$
): \begin{align*} \frac{-2 Y^{(j)}_i}{S^{(d-1)}_i} + \frac{2y_j(i/n)}{s_{d-1}(i/n)} &= \frac{-2 S^{(j)}_i + 2ns_j(i/n) + 2 S^{(j-1)}_i - 2ns_{j-1}(i/n)}{n s_{d-1}(i/n)} \\[4pt] & \ \ \ + 2Y^{(j)}_i \left (\frac{1}{n s_{d-1}(i/n)} - \frac{1}{S^{(d-1)}_i}\right ) \\[4pt]&\geq \frac{-4 E_{first}(i)}{ns_{d-1}(i/n)} + 2Y^{(j)}_i \left (\frac{1}{n s_{d-1}(i/n)} - \frac{1}{S^{(d-1)}_i}\right ) \qquad \text{by (12) and}\ i \lt T \\[4pt] & \geq \frac{-4 E_{first}(i)}{ns_{d-1}(i/n)} - \frac{2 Y^{(j)}_{i} E_{first}(i)}{S^{(d-1)}_i (n s_{d-1}(i/n))} \qquad \text{by (12) and}\ i \lt T\\[4pt] & \geq \frac{-6 E_{first}(i)}{n s_{d-1}(i/n)}. \end{align*}
\begin{align*} \frac{-2 Y^{(j)}_i}{S^{(d-1)}_i} + \frac{2y_j(i/n)}{s_{d-1}(i/n)} &= \frac{-2 S^{(j)}_i + 2ns_j(i/n) + 2 S^{(j-1)}_i - 2ns_{j-1}(i/n)}{n s_{d-1}(i/n)} \\[4pt] & \ \ \ + 2Y^{(j)}_i \left (\frac{1}{n s_{d-1}(i/n)} - \frac{1}{S^{(d-1)}_i}\right ) \\[4pt]&\geq \frac{-4 E_{first}(i)}{ns_{d-1}(i/n)} + 2Y^{(j)}_i \left (\frac{1}{n s_{d-1}(i/n)} - \frac{1}{S^{(d-1)}_i}\right ) \qquad \text{by (12) and}\ i \lt T \\[4pt] & \geq \frac{-4 E_{first}(i)}{ns_{d-1}(i/n)} - \frac{2 Y^{(j)}_{i} E_{first}(i)}{S^{(d-1)}_i (n s_{d-1}(i/n))} \qquad \text{by (12) and}\ i \lt T\\[4pt] & \geq \frac{-6 E_{first}(i)}{n s_{d-1}(i/n)}. \end{align*}
-
2.
 \begin{align*} -\frac{d^2}{d\mu ^2}\left (\frac{ns_j(\mu/n)}{2}\right )\Big |_{\mu = \psi } &= \frac{2}{n}\left (\frac{s_{d-1}(\psi/n)(y_{j-1}(\psi/n) - y_j(\psi/n))+y_j(\psi/n)y_{d-1}(\psi/n)}{(s_{d-1}(\psi/n))^3} \right ) \\[4pt]&= O\left (\frac{1}{dn-2i}\right ) \qquad \text{by (9)}. \end{align*}
\begin{align*} -\frac{d^2}{d\mu ^2}\left (\frac{ns_j(\mu/n)}{2}\right )\Big |_{\mu = \psi } &= \frac{2}{n}\left (\frac{s_{d-1}(\psi/n)(y_{j-1}(\psi/n) - y_j(\psi/n))+y_j(\psi/n)y_{d-1}(\psi/n)}{(s_{d-1}(\psi/n))^3} \right ) \\[4pt]&= O\left (\frac{1}{dn-2i}\right ) \qquad \text{by (9)}. \end{align*}
-
3. For some
 $\phi \in [i,i+1]$
:(13)
$\phi \in [i,i+1]$
:(13) \begin{align} E_{first}(i+1) - E_{first}(i) &= \frac{dE_{first}(\mu )}{d\mu } \Big |_{\mu = \phi } \nonumber \\[4pt]&= 8d^{4d+1} n^{4d+0.6} \left (dn-2\phi \right )^{-4d-1} \nonumber \\[4pt]&= (1 + o(1))\frac{8dE_{first}(i)}{dn - 2i}. \end{align}
\begin{align} E_{first}(i+1) - E_{first}(i) &= \frac{dE_{first}(\mu )}{d\mu } \Big |_{\mu = \phi } \nonumber \\[4pt]&= 8d^{4d+1} n^{4d+0.6} \left (dn-2\phi \right )^{-4d-1} \nonumber \\[4pt]&= (1 + o(1))\frac{8dE_{first}(i)}{dn - 2i}. \end{align}
Now we put the three bounds together:
 \begin{align*} \mathbb{E}\left[Y_{i+1}^- - Y_i^- \mid G_i\right] &\geq \frac{7dE_{first}(i)}{dn - 2i} - \frac{6 E_{first}(i)}{n s_{d-1}(i/n)} + O\left (\frac{1}{dn-2i}\right ) \\[4pt]&\geq \frac{dE_{first}(i) + O(1)}{dn - 2i} \qquad \text{by (9)} \\[4pt]&\geq 0. \end{align*}
\begin{align*} \mathbb{E}\left[Y_{i+1}^- - Y_i^- \mid G_i\right] &\geq \frac{7dE_{first}(i)}{dn - 2i} - \frac{6 E_{first}(i)}{n s_{d-1}(i/n)} + O\left (\frac{1}{dn-2i}\right ) \\[4pt]&\geq \frac{dE_{first}(i) + O(1)}{dn - 2i} \qquad \text{by (9)} \\[4pt]&\geq 0. \end{align*}
Next, we need a Lipschitz condition on each of our variables. Note that
![]() $S^{(j)}_{i+1} - S^{(j)}_{i}$
is either
$S^{(j)}_{i+1} - S^{(j)}_{i}$
is either
![]() $-2, -1$
, or 0; also, one can quickly verify that
$-2, -1$
, or 0; also, one can quickly verify that
![]() $|s_j((i+1)/n) - s_j(i/n)| \leq \frac{2}{n}$
by (5) and (9), and
$|s_j((i+1)/n) - s_j(i/n)| \leq \frac{2}{n}$
by (5) and (9), and
![]() $\big|E_{first}(i+1) - E_{first}(i)\big| = o(1)$
by (13). Hence, we have, for all
$\big|E_{first}(i+1) - E_{first}(i)\big| = o(1)$
by (13). Hence, we have, for all
![]() $i \leq i_{trans}$
and all
$i \leq i_{trans}$
and all
![]() $j$
:
$j$
:
We conclude the proof of Theorem 6 by noting that, by Lemma 7 and (14), we can use the standard Hoeffding-Azuma inequality for martingales (e.g. Theorem 7.2.1 in [Reference Alon and Spencer1]) to show that
![]() $\mathbb{P}\left[W^{(j)+}_{i_{trans}} \gt 0\right]$
and
$\mathbb{P}\left[W^{(j)+}_{i_{trans}} \gt 0\right]$
and
![]() $\mathbb{P}\left[W^{(j)-}_{i_{trans}} \lt 0\right]$
are both
$\mathbb{P}\left[W^{(j)-}_{i_{trans}} \lt 0\right]$
are both
![]() $o(1)$
. For example, for the variable
$o(1)$
. For example, for the variable
![]() $W^{(j)+}_{i}$
one would get
$W^{(j)+}_{i}$
one would get
4. Second phase
The second phase is where the more sophisticated tools will be used, including the use of critical intervals, self-correcting estimates, and a more general martingale inequality. Furthermore, this phase is broken up into
![]() $d-1$
sub-phases, in relation to when each of the
$d-1$
sub-phases, in relation to when each of the
![]() $d-1$
sequences
$d-1$
sequences
![]() $S^{(j)}$
(for
$S^{(j)}$
(for
![]() $j \leq d-2$
) terminate at 0. First, a few definitions: for all
$j \leq d-2$
) terminate at 0. First, a few definitions: for all
![]() $k \in \{0\} \cup [d-2]$
, define
$k \in \{0\} \cup [d-2]$
, define
These step values will govern the endpoints of the sub-phases: define for all
![]() $k \in \{0\} \cup [d-2]$
:
$k \in \{0\} \cup [d-2]$
:
 \begin{align*} I_k \,:\!=\, \left\{\begin{array}{l@{\quad}l} \!\left[i_{trans} + 1, i_{after}(0)\right], & k = 0 \\[4pt]\!\left[i_{after}(k-1) + 1, i_{after}(k)\right], & k \gt 0. \end{array}\right.\end{align*}
\begin{align*} I_k \,:\!=\, \left\{\begin{array}{l@{\quad}l} \!\left[i_{trans} + 1, i_{after}(0)\right], & k = 0 \\[4pt]\!\left[i_{after}(k-1) + 1, i_{after}(k)\right], & k \gt 0. \end{array}\right.\end{align*}
Next, for all
![]() $i,j,k$
such that
$i,j,k$
such that
![]() $0 \leq j \lt d$
,
$0 \leq j \lt d$
,
![]() $0 \leq k \lt d-1$
, and
$0 \leq k \lt d-1$
, and
![]() $i \in I_k$
, define error functions
$i \in I_k$
, define error functions
Note that, by (11), we have
 \begin{equation} E_j(i) = \Theta \left ( \ln (n)^{-0.7d + 0.75 + 0.7j} \left (\frac{dn}{2} - i\right )^{0.7}\right ). \end{equation}
\begin{equation} E_j(i) = \Theta \left ( \ln (n)^{-0.7d + 0.75 + 0.7j} \left (\frac{dn}{2} - i\right )^{0.7}\right ). \end{equation}
Finally, for any
![]() $r \in{\mathbb{R}}_+$
and
$r \in{\mathbb{R}}_+$
and
![]() $\ell \in [d-2]$
, define
$\ell \in [d-2]$
, define
The following Theorem will be proved by induction over the
![]() $d-1$
sub-phases governed by the index
$d-1$
sub-phases governed by the index
![]() $k$
:
$k$
:
Theorem 8.
For each
![]() $k \in \{0\} \cup [d-2]$
:
$k \in \{0\} \cup [d-2]$
:
-
1. With high probability, for all integers
 $j \in [0, d-1]$
and
$j \in [0, d-1]$
and
 $i \in I_k$
:(16)
$i \in I_k$
:(16) \begin{equation} \left |S^{(j)}_{i} - n s_j\left (\frac{i}{n}\right )\right | \leq 4 E_j(i). \end{equation}
\begin{equation} \left |S^{(j)}_{i} - n s_j\left (\frac{i}{n}\right )\right | \leq 4 E_j(i). \end{equation}
-
2.
 $S^{(k)}_{i_{after}(k)} = 0$
with high probability. Furthermore, for any
$S^{(k)}_{i_{after}(k)} = 0$
with high probability. Furthermore, for any
 $k+1$
-tuple
$k+1$
-tuple
 $\{r_0,r_1,\dots,r_k\} \in {({\mathbb{R}}_+ \cup \{0\})^{k+1}}$
:
$\{r_0,r_1,\dots,r_k\} \in {({\mathbb{R}}_+ \cup \{0\})^{k+1}}$
: \begin{equation*} \mathbb{P} \left ( \bigcap _{\ell = 0}^{k} \left (S^{(\ell )}_{\lfloor i(r_{\ell },\ell ) \rfloor } = 0 \right )\right ) \to \exp \left \{-\sum _{\ell =0}^{k} r_{\ell } \right \}.\end{equation*}
\begin{equation*} \mathbb{P} \left ( \bigcap _{\ell = 0}^{k} \left (S^{(\ell )}_{\lfloor i(r_{\ell },\ell ) \rfloor } = 0 \right )\right ) \to \exp \left \{-\sum _{\ell =0}^{k} r_{\ell } \right \}.\end{equation*}
In the end, it is only the second statement with
![]() $k = d-2$
that matters for proving Theorem 1. We make the connection here:
$k = d-2$
that matters for proving Theorem 1. We make the connection here:
Proof of Theorem
1 from Theorem 8. First, note that
![]() $S^{(\ell )}_{\lfloor i(r_{\ell },\ell ) \rfloor } = 0$
is the same as
$S^{(\ell )}_{\lfloor i(r_{\ell },\ell ) \rfloor } = 0$
is the same as
![]() $T_{\ell } \leq i(r_{\ell },\ell )$
, hence by Theorem 8:
$T_{\ell } \leq i(r_{\ell },\ell )$
, hence by Theorem 8:
 \begin{equation*} \mathbb {P} \left ( \bigcap _{\ell = 0}^{d-2} \left (T_{\ell } \leq i(r_{\ell },\ell )\right )\right ) \to \exp \left \{-\sum _{\ell =0}^{d-2} r_{\ell } \right \}.\end{equation*}
\begin{equation*} \mathbb {P} \left ( \bigcap _{\ell = 0}^{d-2} \left (T_{\ell } \leq i(r_{\ell },\ell )\right )\right ) \to \exp \left \{-\sum _{\ell =0}^{d-2} r_{\ell } \right \}.\end{equation*}
Using the Principle of Inclusion-Exclusion plus a simple limiting argument, one can derive
 \begin{equation*}\mathbb {P} \left ( \bigcap _{\ell = 0}^{d-2} \left (\frac {(d-1)!(dn-2T_{\ell })}{\ell !(\ln (n))^{d-1-\ell }} \leq r_{\ell }\right )\right ) = \mathbb {P} \left ( \bigcap _{\ell = 0}^{d-2} \left (T_{\ell } \geq i(r_{\ell },\ell )\right )\right ) \to \prod _{\ell =0}^{d-2} \left(1 - e^{-r_{\ell }}\right),\end{equation*}
\begin{equation*}\mathbb {P} \left ( \bigcap _{\ell = 0}^{d-2} \left (\frac {(d-1)!(dn-2T_{\ell })}{\ell !(\ln (n))^{d-1-\ell }} \leq r_{\ell }\right )\right ) = \mathbb {P} \left ( \bigcap _{\ell = 0}^{d-2} \left (T_{\ell } \geq i(r_{\ell },\ell )\right )\right ) \to \prod _{\ell =0}^{d-2} \left(1 - e^{-r_{\ell }}\right),\end{equation*}
hence the
![]() $d-1$
-dimensional random vector with entries
$d-1$
-dimensional random vector with entries
![]() $V_{n}^{(\ell )} = \frac{(d-1)!(dn-2T_{\ell })}{\ell !(\ln (n))^{d-1-\ell }}$
converges in distribution to the product of
$V_{n}^{(\ell )} = \frac{(d-1)!(dn-2T_{\ell })}{\ell !(\ln (n))^{d-1-\ell }}$
converges in distribution to the product of
![]() $d-1$
independent exponential variables of mean 1.
$d-1$
independent exponential variables of mean 1.
The rest of this section is for proving the first statement of Theorem 8 (for some fixed
![]() $k$
using induction), and Section 5 will be for proving the second statement (again, for some fixed
$k$
using induction), and Section 5 will be for proving the second statement (again, for some fixed
![]() $k$
using induction, assuming the first statement holds for the same
$k$
using induction, assuming the first statement holds for the same
![]() $k$
). Hence, for the rest of the paper we will fix some
$k$
). Hence, for the rest of the paper we will fix some
![]() $k \in \{0\} \cup [d-2]$
.
$k \in \{0\} \cup [d-2]$
.
First, we note that (16) holds w.h.p. for all
![]() $j \lt k$
by a simple argument: by induction on the second statement of Theorem 8, w.h.p. if
$j \lt k$
by a simple argument: by induction on the second statement of Theorem 8, w.h.p. if
![]() $i \in I_k$
then
$i \in I_k$
then
![]() $S_{i}^{(j)} = 0$
. By (11) and by definition of
$S_{i}^{(j)} = 0$
. By (11) and by definition of
![]() $E_j(i)$
, if
$E_j(i)$
, if
![]() $i \in I_k$
then
$i \in I_k$
then
![]() $ns_{j}(i/n) \ll E_{j}(i)$
, completing the argument.
$ns_{j}(i/n) \ll E_{j}(i)$
, completing the argument.
Next, we prove that (16) holds for
![]() $j = d-1$
if it holds for all other values of
$j = d-1$
if it holds for all other values of
![]() $j$
: by combining (1) and (7), we have
$j$
: by combining (1) and (7), we have
 \begin{align*} \left |S^{(d-1)}_{i} - n s_{d-1}\left (\frac{i}{n}\right )\right | &= \left | \sum _{j=0}^{d-2}\left (S^{(j)}_{i} - n s_{j}\left (\frac{i}{n}\right )\right ) \right | \\[4pt]&\leq \sum _{j=0}^{d-2} 4E_j(i) \qquad \text{by (16) for } j \leq d-2 \\[4pt]&\lt 4 E_{d-1}(i) \qquad \text{by (15).} \end{align*}
\begin{align*} \left |S^{(d-1)}_{i} - n s_{d-1}\left (\frac{i}{n}\right )\right | &= \left | \sum _{j=0}^{d-2}\left (S^{(j)}_{i} - n s_{j}\left (\frac{i}{n}\right )\right ) \right | \\[4pt]&\leq \sum _{j=0}^{d-2} 4E_j(i) \qquad \text{by (16) for } j \leq d-2 \\[4pt]&\lt 4 E_{d-1}(i) \qquad \text{by (15).} \end{align*}
Hence, for the rest of this section, we need to show the first statement of Theorem 8 for
![]() $j \in [k, d-2]$
. From now on we always assume
$j \in [k, d-2]$
. From now on we always assume
![]() $j$
to be in this range. We will also assume that, for all
$j$
to be in this range. We will also assume that, for all
![]() $\lambda \lt k$
,
$\lambda \lt k$
,
![]() $S_{i}^{(\lambda )} = 0$
if
$S_{i}^{(\lambda )} = 0$
if
![]() $i \in I_k$
(which holds w.h.p. from above).
$i \in I_k$
(which holds w.h.p. from above).
In this section we will make use of so-called critical intervals, ranges of possible values for
![]() $S^{(j)}_i$
in which we apply a martingale argument. The lower critical interval will be
$S^{(j)}_i$
in which we apply a martingale argument. The lower critical interval will be
and the upper critical interval will be
Our goal is to show that w.h.p.
![]() $S^{(j)}_i$
does not cross either critical interval; however, we first need to show that
$S^{(j)}_i$
does not cross either critical interval; however, we first need to show that
![]() $S^{(j)}_i$
sits between the critical intervals at the beginning of the phase (this is the reason why
$S^{(j)}_i$
sits between the critical intervals at the beginning of the phase (this is the reason why
![]() $E_j(i)$
has the
$E_j(i)$
has the
![]() $2^k$
factor; it makes a sudden jump in size between phases to accommodate a new martingale process), which is the statement of our first Lemma of this section:
$2^k$
factor; it makes a sudden jump in size between phases to accommodate a new martingale process), which is the statement of our first Lemma of this section:
Lemma 9.
W.h.p., for all
![]() $j \in [k,d-2]$
(putting
$j \in [k,d-2]$
(putting
![]() $i_{after}({-}1) = i_{trans}$
for convenience of notation):
$i_{after}({-}1) = i_{trans}$
for convenience of notation):
Proof. First, recall that
![]() $S^{(j)}_{i+1} - S^{(j)}_{i} \in \{-2,-1,0\}$
and
$S^{(j)}_{i+1} - S^{(j)}_{i} \in \{-2,-1,0\}$
and
![]() $|n s_{j}((i+1)/n) - n s_{j}(i/n)| \leq 2$
for any
$|n s_{j}((i+1)/n) - n s_{j}(i/n)| \leq 2$
for any
![]() $i$
and
$i$
and
![]() $j$
(see paragraph above (14)). Second, consider the change in the bound itself between
$j$
(see paragraph above (14)). Second, consider the change in the bound itself between
![]() $i_{after}(k-1)$
and
$i_{after}(k-1)$
and
![]() $i_{after}(k-1)+1$
: by definitions of
$i_{after}(k-1)+1$
: by definitions of
![]() $i_{trans}, E_{first}, E_j$
, and by (15), we have
$i_{trans}, E_{first}, E_j$
, and by (15), we have
![]() $1 \ll E_{first}(i_{trans}) = \Theta \left(n^{0.64}\right), E_{j}(i_{trans}+1) = \omega \left(n^{0.69}\right)$
, and
$1 \ll E_{first}(i_{trans}) = \Theta \left(n^{0.64}\right), E_{j}(i_{trans}+1) = \omega \left(n^{0.69}\right)$
, and
![]() $1 \ll E_{j}(i_{after}(k-1)) \approx \frac{1}{2}(E_{j}(i_{after}(k-1)+1)$
for
$1 \ll E_{j}(i_{after}(k-1)) \approx \frac{1}{2}(E_{j}(i_{after}(k-1)+1)$
for
![]() $k \gt 0$
. Hence, by induction on the first statement of Theorem 8 and by Theorem 6, the statement of the Lemma follows.
$k \gt 0$
. Hence, by induction on the first statement of Theorem 8 and by Theorem 6, the statement of the Lemma follows.
Next, like in Section 3, we define two new random variables for each
![]() $j$
and
$j$
and
![]() $i \in I_k$
:
$i \in I_k$
:
 \begin{align*} S^{(j)+}_{i} &\,:\!=\, S^{(j)}_i - n s_j(i/n) - 4 E_j(i)\\[3pt] S^{(j)-}_{i} &\,:\!=\, S^{(j)}_i - n s_j(i/n) + 4 E_j(i). \end{align*}
\begin{align*} S^{(j)+}_{i} &\,:\!=\, S^{(j)}_i - n s_j(i/n) - 4 E_j(i)\\[3pt] S^{(j)-}_{i} &\,:\!=\, S^{(j)}_i - n s_j(i/n) + 4 E_j(i). \end{align*}
We also re-introduce the stopping time
![]() $T$
, now defined as the first step
$T$
, now defined as the first step
![]() $i \in I_k$
for which (16) is not satisfied for some
$i \in I_k$
for which (16) is not satisfied for some
![]() $j$
; if (16) always holds, then let
$j$
; if (16) always holds, then let
![]() $T = \infty$
. Let variable name
$T = \infty$
. Let variable name
![]() $W$
be introduced to equip this stopping time to variable
$W$
be introduced to equip this stopping time to variable
![]() $S$
, i.e.
$S$
, i.e.
 \begin{align*} W^{(j)+}_{i} \,:\!=\, \begin{cases} S^{(j)+}_{i}, i \lt T \\[5pt] S^{(j)+}_{T}, i \geq T \end{cases} \quad W^{(j)-}_i \,:\!=\, \begin{cases} S^{(j)-}_i, i \lt T \\[5pt] S^{(j)-}_T, i \geq T. \end{cases} \end{align*}
\begin{align*} W^{(j)+}_{i} \,:\!=\, \begin{cases} S^{(j)+}_{i}, i \lt T \\[5pt] S^{(j)+}_{T}, i \geq T \end{cases} \quad W^{(j)-}_i \,:\!=\, \begin{cases} S^{(j)-}_i, i \lt T \\[5pt] S^{(j)-}_T, i \geq T. \end{cases} \end{align*}
Note that
![]() $W^{(j)+}_{i}$
corresponds to the upper critical interval, and
$W^{(j)+}_{i}$
corresponds to the upper critical interval, and
![]() $W^{(j)-}_i$
to the lower one. Furthermore, the inequality of Theorem 8 holds if and only if
$W^{(j)-}_i$
to the lower one. Furthermore, the inequality of Theorem 8 holds if and only if
![]() $W^{(j)+}_{i_{after}(k)} \leq 0$
and
$W^{(j)+}_{i_{after}(k)} \leq 0$
and
![]() $W^{(j)-}_{i_{after}(k)} \geq 0$
for each
$W^{(j)-}_{i_{after}(k)} \geq 0$
for each
![]() $j$
(here we must make use of our assumption that
$j$
(here we must make use of our assumption that
![]() $S_{i}^{(\lambda )} = 0$
for all
$S_{i}^{(\lambda )} = 0$
for all
![]() $\lambda \lt k$
). The next Lemma states that, within their respective critical intervals, they are a supermartingale and submartingale respectively:
$\lambda \lt k$
). The next Lemma states that, within their respective critical intervals, they are a supermartingale and submartingale respectively:
Lemma 10.
For all
![]() $i \in I_k$
and for all
$i \in I_k$
and for all
![]() $j \in [k,d-2], \ \mathbb{E}\left[W^{(j)-}_{i+1} - W^{(j)-}_i \mid G_i\right] \geq 0$
whenever
$j \in [k,d-2], \ \mathbb{E}\left[W^{(j)-}_{i+1} - W^{(j)-}_i \mid G_i\right] \geq 0$
whenever
![]() $W^{(j)-}_i \leq E_j(i)$
, and
$W^{(j)-}_i \leq E_j(i)$
, and
![]() $\mathbb{E}\left[W^{(j)+}_{i+1} - W^{(j)+}_i \mid G_i\right] \leq 0$
whenever
$\mathbb{E}\left[W^{(j)+}_{i+1} - W^{(j)+}_i \mid G_i\right] \leq 0$
whenever
![]() $W^{(j)+}_i \geq -E_j(i)$
.
$W^{(j)+}_i \geq -E_j(i)$
.
Proof. Here we just prove the first part of the Lemma; the second part follows from nearly identical calculations. By the same logic as in the proof of Lemma 7 we work with
![]() $S^{(j)-}$
instead of
$S^{(j)-}$
instead of
![]() $W^{(j)-}$
and assume that (16) holds for all
$W^{(j)-}$
and assume that (16) holds for all
![]() $j$
. We also have the same expected change as in Lemma 7, except with
$j$
. We also have the same expected change as in Lemma 7, except with
![]() $E_{first}(i)$
replaced with
$E_{first}(i)$
replaced with
![]() $4E_j(i)$
:
$4E_j(i)$
:
 \begin{align*} \mathbb{E}\left[S^{(j)-}_{i+1} - S^{(j)-}_i \mid G_i\right] &= \frac{-2 Y^{(j)}_i}{S^{(d-1)}_i} + O\left (\frac{1}{dn-2i}\right ) + \frac{2y_j(i/n)}{s_{d-1}(i/n)} -\frac{d^2}{d\mu ^2}\left (\frac{ns_j(\mu/n)}{2}\right )\Big |_{\mu = \psi } \\& \quad + 4(E_{j}(i+1) - E_j(i)). \end{align*}
\begin{align*} \mathbb{E}\left[S^{(j)-}_{i+1} - S^{(j)-}_i \mid G_i\right] &= \frac{-2 Y^{(j)}_i}{S^{(d-1)}_i} + O\left (\frac{1}{dn-2i}\right ) + \frac{2y_j(i/n)}{s_{d-1}(i/n)} -\frac{d^2}{d\mu ^2}\left (\frac{ns_j(\mu/n)}{2}\right )\Big |_{\mu = \psi } \\& \quad + 4(E_{j}(i+1) - E_j(i)). \end{align*}
We split the above expression
![]() $\Big($
excluding
$\Big($
excluding
![]() $O\left (\frac{1}{dn-2i}\right )\Big)$
into three summands, assuming
$O\left (\frac{1}{dn-2i}\right )\Big)$
into three summands, assuming
![]() $S^{(j)-}_i \leq E_j(i) \ \Longleftrightarrow \ S^{(j)}_i - ns_j(i/n) \leq - 3E_j(i)$
$S^{(j)-}_i \leq E_j(i) \ \Longleftrightarrow \ S^{(j)}_i - ns_j(i/n) \leq - 3E_j(i)$
![]() $\big($
for convenience, for the case
$\big($
for convenience, for the case
![]() $j = 0$
, we put
$j = 0$
, we put
![]() $S_i^{(j-1)}, s_{j-1}$
, and
$S_i^{(j-1)}, s_{j-1}$
, and
![]() $E_{j-1}$
all equal to 0
$E_{j-1}$
all equal to 0
![]() $\big)$
:
$\big)$
:
-
1.
 \begin{align*} \frac{-2 Y^{(j)}_i}{S^{(d-1)}_i} + \frac{2y_j(i/n)}{s_{d-1}(i/n)} &= \frac{-2 S^{(j)}_i + 2ns_j(i/n) + 2 S^{(j-1)}_i - 2ns_{j-1}(i/n)}{n s_{d-1}(i/n)} \\[3pt] & \ \ \ + 2Y^{(j)}_i \left (\frac{1}{n s_{d-1}(i/n)} - \frac{1}{S^{(d-1)}_i}\right ) \\[3pt]&\geq \frac{6 E_j(i) - 8 E_{j-1}(i)}{ns_{d-1}(i/n)} - \frac{8 S^{(j)}_{i} E_{d-1}(i)}{S^{(d-1)}_i (n s_{d-1}(i/n))} \qquad \text{by (16)} \\[3pt]&\geq \frac{5.9 E_j(i)}{ns_{d-1}(i/n)} - \frac{9 S^{(j)}_{i} E_{d-1}(i)}{(n s_{d-1}(i/n))^2} \qquad \text{by (15), (16), (11), and } i \leq i_{after}(k) \\[3pt]&\geq \frac{5.9 E_j(i)}{ns_{d-1}(i/n)} - \frac{9 (n s_{j}(i/n)) E_{d-1}(i)}{(n s_{d-1}(i/n))^2} - \frac{36 E_{j}(i) E_{d-1}(i)}{(n s_{d-1}(i/n))^2} \qquad \text{by (16)} \\[3pt]&= \left (\frac{E_j(i)}{n s_{d-1}(i/n)}\right )\left (5.9 - 9\left (\frac{s_{j}(i/n)}{s_{d-1}(i/n)}\right )^{0.3} - \frac{36*2^k \ln (n)^{0.05}}{(n s_{d-1}(i/n))^{0.3}}\right ) \\[3pt]&\geq \frac{5.8 E_j(i)}{n s_{d-1}(i/n)} \qquad \text{by } i \leq i_{after}(k)\ \text{and}\ (11). \end{align*}
\begin{align*} \frac{-2 Y^{(j)}_i}{S^{(d-1)}_i} + \frac{2y_j(i/n)}{s_{d-1}(i/n)} &= \frac{-2 S^{(j)}_i + 2ns_j(i/n) + 2 S^{(j-1)}_i - 2ns_{j-1}(i/n)}{n s_{d-1}(i/n)} \\[3pt] & \ \ \ + 2Y^{(j)}_i \left (\frac{1}{n s_{d-1}(i/n)} - \frac{1}{S^{(d-1)}_i}\right ) \\[3pt]&\geq \frac{6 E_j(i) - 8 E_{j-1}(i)}{ns_{d-1}(i/n)} - \frac{8 S^{(j)}_{i} E_{d-1}(i)}{S^{(d-1)}_i (n s_{d-1}(i/n))} \qquad \text{by (16)} \\[3pt]&\geq \frac{5.9 E_j(i)}{ns_{d-1}(i/n)} - \frac{9 S^{(j)}_{i} E_{d-1}(i)}{(n s_{d-1}(i/n))^2} \qquad \text{by (15), (16), (11), and } i \leq i_{after}(k) \\[3pt]&\geq \frac{5.9 E_j(i)}{ns_{d-1}(i/n)} - \frac{9 (n s_{j}(i/n)) E_{d-1}(i)}{(n s_{d-1}(i/n))^2} - \frac{36 E_{j}(i) E_{d-1}(i)}{(n s_{d-1}(i/n))^2} \qquad \text{by (16)} \\[3pt]&= \left (\frac{E_j(i)}{n s_{d-1}(i/n)}\right )\left (5.9 - 9\left (\frac{s_{j}(i/n)}{s_{d-1}(i/n)}\right )^{0.3} - \frac{36*2^k \ln (n)^{0.05}}{(n s_{d-1}(i/n))^{0.3}}\right ) \\[3pt]&\geq \frac{5.8 E_j(i)}{n s_{d-1}(i/n)} \qquad \text{by } i \leq i_{after}(k)\ \text{and}\ (11). \end{align*}
-
2. Just as in the proof of Lemma 7:
 \begin{equation*} -\frac {d^2}{d\mu ^2}\left (\frac {ns_j(\mu/n)}{2}\right )\Big |_{\mu = \psi } = O\left (\frac {1}{dn-2i}\right ). \end{equation*}
\begin{equation*} -\frac {d^2}{d\mu ^2}\left (\frac {ns_j(\mu/n)}{2}\right )\Big |_{\mu = \psi } = O\left (\frac {1}{dn-2i}\right ). \end{equation*}
-
3.
(17) \begin{align} 4(E_j(i+1) - E_j(i)) &= 4 \frac{dE_j(\mu )}{d\mu }\Big |_{\mu = \phi } \qquad \text{for some}\ \phi \in [i, i+1] \nonumber \\[4pt]&= (4)(2^k) \ln (n)^{0.05} \left (\frac{0.7}{(ns_j(\phi/n))^{0.3}}\right )\left (\frac{-2y_j(\phi/n)}{s_{d-1}(\phi/n)}\right ) \qquad \text{by (5)} \nonumber \\[4pt]& = (4 + o(1))(2^k) \ln (n)^{0.05} \left (\frac{0.7}{(ns_j(\phi/n))^{0.3}}\right )\left (\frac{-2s_j(\phi/n)}{s_{d-1}(\phi/n)}\right ) \ \ \ \ \text{by (10)} \nonumber \\[4pt]&= \frac{-(5.6 + o(1)) E_j(\phi )}{n s_{d-1}(\phi/n)} = \frac{-(5.6 + o(1))E_j(i)}{n s_{d-1}(i/n)}. \end{align}
\begin{align} 4(E_j(i+1) - E_j(i)) &= 4 \frac{dE_j(\mu )}{d\mu }\Big |_{\mu = \phi } \qquad \text{for some}\ \phi \in [i, i+1] \nonumber \\[4pt]&= (4)(2^k) \ln (n)^{0.05} \left (\frac{0.7}{(ns_j(\phi/n))^{0.3}}\right )\left (\frac{-2y_j(\phi/n)}{s_{d-1}(\phi/n)}\right ) \qquad \text{by (5)} \nonumber \\[4pt]& = (4 + o(1))(2^k) \ln (n)^{0.05} \left (\frac{0.7}{(ns_j(\phi/n))^{0.3}}\right )\left (\frac{-2s_j(\phi/n)}{s_{d-1}(\phi/n)}\right ) \ \ \ \ \text{by (10)} \nonumber \\[4pt]&= \frac{-(5.6 + o(1)) E_j(\phi )}{n s_{d-1}(\phi/n)} = \frac{-(5.6 + o(1))E_j(i)}{n s_{d-1}(i/n)}. \end{align}
Now we put the above bounds together (using (11), (15), and
![]() $i \leq i_{after}(k) \leq i_{after}(j)$
):
$i \leq i_{after}(k) \leq i_{after}(j)$
):
 \begin{align*} \mathbb{E}\left[S_{i+1}^{(j)-} - S_{i}^{(j)-} \mid G_i\right] &\geq \frac{0.01E_j(i)}{n s_{d-1}(i/n)} + O\left (\frac{1}{dn-2i}\right ) \\&\geq 0. \end{align*}
\begin{align*} \mathbb{E}\left[S_{i+1}^{(j)-} - S_{i}^{(j)-} \mid G_i\right] &\geq \frac{0.01E_j(i)}{n s_{d-1}(i/n)} + O\left (\frac{1}{dn-2i}\right ) \\&\geq 0. \end{align*}
We introduce the next Lemma to get sufficiently small bounds on the one-step changes in each time step (this is known as the “bounded hypothesis” from [Reference Wormald14]):
Lemma 11.
For all
![]() $i \in I_k$
and all
$i \in I_k$
and all
![]() $j \in [k,d-2]$
,
$j \in [k,d-2]$
,
where “
![]() $\xi$
” can be either “
$\xi$
” can be either “
![]() $+$
” or “
$+$
” or “
![]() $-$
”.
$-$
”.
Proof. Like in the proofs of Lemma 7 and 10, we assume that
![]() $W^{\xi } = S^{(j)\xi }$
(
$W^{\xi } = S^{(j)\xi }$
(
![]() $\xi$
is
$\xi$
is
![]() $+$
or
$+$
or
![]() $-$
), else
$-$
), else
![]() $W^{\xi }_{i+1} - W^{\xi }_{i} = 0$
. Again, we have
$W^{\xi }_{i+1} - W^{\xi }_{i} = 0$
. Again, we have
![]() $-2 \leq S^{(j)}_{i+1} - S^{(j)}_{i} \leq 0$
. Secondly, we have
$-2 \leq S^{(j)}_{i+1} - S^{(j)}_{i} \leq 0$
. Secondly, we have
 \begin{align*} & |-n s_j((i+1)/n)+ns_j(i/n) - C E_j(i+1)+C E_j(i)| \\[3pt] & \leq |-n s_j((i+1)/n)+ns_j(i/n)| + |- C E_j(i+1)+C E_j(i)| \\[3pt] &= O \left (\frac{y_j(i/n)}{s_{d-1}(i/n)} + \frac{E_j(i)}{n s_{d-1}(i/n)} \right ) \qquad \text{by (5), (11), and (17)} \\[3pt] &= o\left(\ln (n)^{-d+ 1.06+j}\right) \qquad \text{by (11), (15), and } i \leq i_{after}(k) \leq i_{after}(j). \end{align*}
\begin{align*} & |-n s_j((i+1)/n)+ns_j(i/n) - C E_j(i+1)+C E_j(i)| \\[3pt] & \leq |-n s_j((i+1)/n)+ns_j(i/n)| + |- C E_j(i+1)+C E_j(i)| \\[3pt] &= O \left (\frac{y_j(i/n)}{s_{d-1}(i/n)} + \frac{E_j(i)}{n s_{d-1}(i/n)} \right ) \qquad \text{by (5), (11), and (17)} \\[3pt] &= o\left(\ln (n)^{-d+ 1.06+j}\right) \qquad \text{by (11), (15), and } i \leq i_{after}(k) \leq i_{after}(j). \end{align*}
Combining the inequalities completes the proof.
To put this all together to prove the first part of Theorem 8, we introduce a series of events: first, let
![]() $\mathcal{E}^{(j)+}$
denote the event that
$\mathcal{E}^{(j)+}$
denote the event that
![]() $W^{(j)+}_{i_{after}(k)} \gt 0$
and
$W^{(j)+}_{i_{after}(k)} \gt 0$
and
![]() $\mathcal{E}^{(j)-}$
denote the event that
$\mathcal{E}^{(j)-}$
denote the event that
![]() $W^{(j)-}_{i_{after}(k)} \lt 0$
. Let
$W^{(j)-}_{i_{after}(k)} \lt 0$
. Let
![]() $\mathcal{E} = \left (\bigcup _{j \geq k}\mathcal{E}^{(j)+}\right ) \cup \left (\bigcup _{j \geq k}\mathcal{E}^{(j)-}\right )$
; we seek to bound
$\mathcal{E} = \left (\bigcup _{j \geq k}\mathcal{E}^{(j)+}\right ) \cup \left (\bigcup _{j \geq k}\mathcal{E}^{(j)-}\right )$
; we seek to bound
![]() $\mathbb{P}[\mathcal{E}]$
, since
$\mathbb{P}[\mathcal{E}]$
, since
![]() $\mathcal{E}$
is the event that (16) doesn’t hold for some
$\mathcal{E}$
is the event that (16) doesn’t hold for some
![]() $i \in I_k$
. Next, for all
$i \in I_k$
. Next, for all
![]() $\ell \in I_k$
, let
$\ell \in I_k$
, let
![]() $\mathcal{H}^{(j)+}_{\ell }$
be the event that
$\mathcal{H}^{(j)+}_{\ell }$
be the event that
![]() $W^{(j)+}_{\ell - 1} \lt -E_j(\ell - 1)$
and
$W^{(j)+}_{\ell - 1} \lt -E_j(\ell - 1)$
and
![]() $W^{(j)+}_{\ell } \geq -E_j(\ell )$
, and let
$W^{(j)+}_{\ell } \geq -E_j(\ell )$
, and let
![]() $\Big($
see Fig. 1 for a visual representation of event
$\Big($
see Fig. 1 for a visual representation of event
![]() $\mathcal{E}^{(j)+}_{\ell }\Big)$
$\mathcal{E}^{(j)+}_{\ell }\Big)$

Figure 1. Visual representation of event
![]() $\mathcal{E}^{(j)+}_{\ell }$
.
$\mathcal{E}^{(j)+}_{\ell }$
.
Similarly, for all
![]() $\ell \in I_k$
, let
$\ell \in I_k$
, let
![]() $\mathcal{H}^{(j)-}_{\ell }$
be the event that
$\mathcal{H}^{(j)-}_{\ell }$
be the event that
![]() $W^{(j)-}_{\ell - 1} \gt E_j(\ell - 1)$
and
$W^{(j)-}_{\ell - 1} \gt E_j(\ell - 1)$
and
![]() $W^{(j)-}_{\ell } \leq E_j(\ell )$
, and let
$W^{(j)-}_{\ell } \leq E_j(\ell )$
, and let
Finally, note that, by Lemma 9, with high probability we must have
Furthermore, assuming these two inequalities hold (and, once again, assuming that
![]() $S^{\lambda }_i = 0$
if
$S^{\lambda }_i = 0$
if
![]() $\lambda \lt k$
), then if
$\lambda \lt k$
), then if
![]() $W^{(j)+}_{i_{after}(k)} \gt 0$
for some
$W^{(j)+}_{i_{after}(k)} \gt 0$
for some
![]() $j$
, one of the events
$j$
, one of the events
![]() $\mathcal{E}^{(j)+}_{\ell }$
must happen; likewise, if
$\mathcal{E}^{(j)+}_{\ell }$
must happen; likewise, if
![]() $W^{(j)-}_{i_{after}(k)} \lt 0$
for some
$W^{(j)-}_{i_{after}(k)} \lt 0$
for some
![]() $j$
, one of the events
$j$
, one of the events
![]() $\mathcal{E}^{(j)-}_{\ell }$
must happen; hence,
$\mathcal{E}^{(j)-}_{\ell }$
must happen; hence,
![]() $\mathcal{E}^{(j)+} = \displaystyle \bigcup _{\ell } \mathcal{E}^{(j)+}_{\ell }$
and
$\mathcal{E}^{(j)+} = \displaystyle \bigcup _{\ell } \mathcal{E}^{(j)+}_{\ell }$
and
![]() $\mathcal{E}^{(j)-} = \displaystyle \bigcup _{\ell } \mathcal{E}^{(j)-}_{\ell }$
.
$\mathcal{E}^{(j)-} = \displaystyle \bigcup _{\ell } \mathcal{E}^{(j)-}_{\ell }$
.
We are now ready to prove the first statement of Theorem 8 in full.
Proof of the first part of Theorem
8 with fixed
![]() $k$
. First, we fix an arbitrary
$k$
. First, we fix an arbitrary
![]() $j$
(in
$j$
(in
![]() $[k,d-2]$
). We prove that
$[k,d-2]$
). We prove that
![]() $\mathbb{P}\big[\mathcal{E}^{(j)-}\big] = \exp \big\{-\Omega \big(\ln (n)^{0.036}\big)\big\}$
; the proof for bounding
$\mathbb{P}\big[\mathcal{E}^{(j)-}\big] = \exp \big\{-\Omega \big(\ln (n)^{0.036}\big)\big\}$
; the proof for bounding
![]() $\mathbb{P}\big[\mathcal{E}^{(j)+}\big]$
is nearly identical. We will use Corollary 5 to bound
$\mathbb{P}\big[\mathcal{E}^{(j)+}\big]$
is nearly identical. We will use Corollary 5 to bound
![]() $\mathbb{P}\big[\mathcal{E}^{(j)-}_{\ell }\big]$
for each fixed
$\mathbb{P}\big[\mathcal{E}^{(j)-}_{\ell }\big]$
for each fixed
![]() $\ell$
. Given a fixed
$\ell$
. Given a fixed
![]() $\ell$
, we define a modified stopping time
$\ell$
, we define a modified stopping time
(letting
![]() $T_{mod} = \infty$
if the condition doesn’t hold for any
$T_{mod} = \infty$
if the condition doesn’t hold for any
![]() $i$
in the range). Let variable
$i$
in the range). Let variable
![]() $W^{\ell }_i$
be the variable
$W^{\ell }_i$
be the variable
![]() $W^{(j)-}_{i}$
defined just on
$W^{(j)-}_{i}$
defined just on
![]() $i \in [\ell, i_{after}(k)]$
equipped with this stopping time (we drop the “
$i \in [\ell, i_{after}(k)]$
equipped with this stopping time (we drop the “
![]() $(j)-$
” here for convenience); i.e.
$(j)-$
” here for convenience); i.e.
 \begin{equation*} W^{\ell }_i \,:\!=\, \begin {cases} W^{(j)-}_i, i \lt T_{mod} \\[4pt] W^{(j)-}_{T_{mod}}, i \geq T_{mod}. \end {cases} \end{equation*}
\begin{equation*} W^{\ell }_i \,:\!=\, \begin {cases} W^{(j)-}_i, i \lt T_{mod} \\[4pt] W^{(j)-}_{T_{mod}}, i \geq T_{mod}. \end {cases} \end{equation*}
Note that
![]() $\big(W^{\ell }_i\big)_i$
(over
$\big(W^{\ell }_i\big)_i$
(over
![]() $i \in [\ell,i_{after}(k)]$
) is a submartingale by Lemma 10, since our new stopping time negates the need for the condition
$i \in [\ell,i_{after}(k)]$
) is a submartingale by Lemma 10, since our new stopping time negates the need for the condition
![]() $W^{(j)-}_i \leq E_j(i)$
; also,
$W^{(j)-}_i \leq E_j(i)$
; also,
![]() $\big(W^{\ell }_i\big)_i$
satisfies Lemma 11. Since we want an upper bound for
$\big(W^{\ell }_i\big)_i$
satisfies Lemma 11. Since we want an upper bound for
![]() $\mathbb{P}\big[\mathcal{E}^{(j)-}_{\ell }\big]$
, we can condition on event
$\mathbb{P}\big[\mathcal{E}^{(j)-}_{\ell }\big]$
, we can condition on event
![]() $\mathcal{H}^{(j)-}_{\ell }$
, as
$\mathcal{H}^{(j)-}_{\ell }$
, as
![]() $\mathcal{H}^{(j)-}_{\ell } \supseteq \mathcal{E}^{(j)-}_{\ell }$
. Now let
$\mathcal{H}^{(j)-}_{\ell } \supseteq \mathcal{E}^{(j)-}_{\ell }$
. Now let
 \begin{align*} A_i &= -W_{\ell +i}^{\ell } + W^{\ell }_{\ell },\\ \eta &= \ln (n)^{-d+1.06+j}, \\ N &= 3, \\ m &= i_{after}(k) - \ell,\\ a &= 0.9 E_j(\ell ). \end{align*}
\begin{align*} A_i &= -W_{\ell +i}^{\ell } + W^{\ell }_{\ell },\\ \eta &= \ln (n)^{-d+1.06+j}, \\ N &= 3, \\ m &= i_{after}(k) - \ell,\\ a &= 0.9 E_j(\ell ). \end{align*}
Note that the conditions of Corollary 5 are satisfied:
![]() $0 = A_0$
and
$0 = A_0$
and
![]() $\eta \lt N/10$
are obvious, Lemma 11 gives us
$\eta \lt N/10$
are obvious, Lemma 11 gives us
![]() $-\eta \leq A_{i+1} - A_{i} \leq N$
, and
$-\eta \leq A_{i+1} - A_{i} \leq N$
, and
![]() $(A_i)_i$
is a supermartingale since
$(A_i)_i$
is a supermartingale since
![]() $\big(W^{\ell }_i\big)_i$
is a submartingale. We therefore implement Corollary 5, using
$\big(W^{\ell }_i\big)_i$
is a submartingale. We therefore implement Corollary 5, using
![]() $m \leq \frac{dn}{2} - \ell \leq d n s_{d-1}(\ell/n)$
(by (9)), (11), and (15):
$m \leq \frac{dn}{2} - \ell \leq d n s_{d-1}(\ell/n)$
(by (9)), (11), and (15):
To bound
![]() $\mathbb{P}\big[\mathcal{E}^{(j)-}_{\ell }\big]$
, we show that
$\mathbb{P}\big[\mathcal{E}^{(j)-}_{\ell }\big]$
, we show that
![]() $\mathcal{E}^{(j)-}_{\ell } \subseteq \{ A_m \geq a\}$
and apply (18) while conditioning on
$\mathcal{E}^{(j)-}_{\ell } \subseteq \{ A_m \geq a\}$
and apply (18) while conditioning on
![]() $\mathcal{H}^{(j)-}_{\ell }$
. Given
$\mathcal{H}^{(j)-}_{\ell }$
. Given
![]() $\mathcal{H}^{(j)-}_{\ell }$
happens, we have
$\mathcal{H}^{(j)-}_{\ell }$
happens, we have
![]() $W^{\ell }_{\ell } = W^{(j)-}_{\ell } \gt 0.9 E_j(\ell ) = a$
by (15), Lemma 11, and
$W^{\ell }_{\ell } = W^{(j)-}_{\ell } \gt 0.9 E_j(\ell ) = a$
by (15), Lemma 11, and
![]() $i \leq i_{after}(j)$
. Therefore
$i \leq i_{after}(j)$
. Therefore
![]() $\mathcal{E}^{(j)-}_{\ell } = \mathcal{H}^{(j)-}_{\ell } \cap \left\{ W^{\ell }_{i_{after}(k)} \lt 0 \right\} \subseteq \{A_m \geq a\}$
, hence
$\mathcal{E}^{(j)-}_{\ell } = \mathcal{H}^{(j)-}_{\ell } \cap \left\{ W^{\ell }_{i_{after}(k)} \lt 0 \right\} \subseteq \{A_m \geq a\}$
, hence
We now take a union bound to bound
![]() $\mathbb{P}\big[\mathcal{E}^{(j)-}\big]$
(using (11) where appropriate):
$\mathbb{P}\big[\mathcal{E}^{(j)-}\big]$
(using (11) where appropriate):
 \begin{align*} \mathbb{P}\big[\mathcal{E}^{(j)-}\big] &\leq \sum _{\ell = i_{after}(k-1)+1}^{i_{after}(k)} \mathbb{P}\left [\mathcal{E}^{(j)-}_{\ell }\right ] \\[3pt] = & \sum _{\ell =i_{trans}}^{i_{after}(k)} \left (\exp \left \{-\Omega \left(\ln (n)^{0.04}(n s_j(\ell/n))^{0.4}\right)\right \} + \exp \left \{-\Omega \left(\ln (n)^{0.05}(n s_j(\ell/n))^{0.7}\right)\right \} \right )\\[3pt] = & \sum _{\ell =i_{trans}}^{i_{after}(j)} \left (\exp \left \{- \Omega \left (\frac{(dn-2\ell )^{0.4}}{\ln (n)^{0.4d-0.44-0.4j}}\right )\right \} + \exp \left \{- \Omega \left (\frac{(dn-2\ell )^{0.7}}{\ln (n)^{0.7d-0.75-0.7j}}\right )\right \}\right ) \\[3pt] = & \sum _{p =\lfloor \ln (n)^{d-1.01-j}\rfloor }^{\lceil n^{1 - 1/(100d)}\rceil } \left ( \exp \left \{- \Omega \left (\frac{p^{0.4}}{\ln (n)^{0.4d-0.44-0.4j}}\right )\right \} + \exp \left \{- \Omega \left (\frac{p^{0.7}}{\ln (n)^{0.7d-0.75-0.7j}}\right )\right \} \right )\\[3pt] = & \ln (n)^{d-1.01-j}\sum _{q=1}^{\infty } \left (\exp \left \{-\Omega \left(q^{0.4} \ln (n)^{0.036}\right)\right \} + \exp \left \{-\Omega \left(q^{0.7} \ln (n)^{0.043}\right)\right \}\right ) \\[3pt]=& \exp \left\{-\Omega \left(\ln (n)^{0.036}\right)\right\}. \end{align*}
\begin{align*} \mathbb{P}\big[\mathcal{E}^{(j)-}\big] &\leq \sum _{\ell = i_{after}(k-1)+1}^{i_{after}(k)} \mathbb{P}\left [\mathcal{E}^{(j)-}_{\ell }\right ] \\[3pt] = & \sum _{\ell =i_{trans}}^{i_{after}(k)} \left (\exp \left \{-\Omega \left(\ln (n)^{0.04}(n s_j(\ell/n))^{0.4}\right)\right \} + \exp \left \{-\Omega \left(\ln (n)^{0.05}(n s_j(\ell/n))^{0.7}\right)\right \} \right )\\[3pt] = & \sum _{\ell =i_{trans}}^{i_{after}(j)} \left (\exp \left \{- \Omega \left (\frac{(dn-2\ell )^{0.4}}{\ln (n)^{0.4d-0.44-0.4j}}\right )\right \} + \exp \left \{- \Omega \left (\frac{(dn-2\ell )^{0.7}}{\ln (n)^{0.7d-0.75-0.7j}}\right )\right \}\right ) \\[3pt] = & \sum _{p =\lfloor \ln (n)^{d-1.01-j}\rfloor }^{\lceil n^{1 - 1/(100d)}\rceil } \left ( \exp \left \{- \Omega \left (\frac{p^{0.4}}{\ln (n)^{0.4d-0.44-0.4j}}\right )\right \} + \exp \left \{- \Omega \left (\frac{p^{0.7}}{\ln (n)^{0.7d-0.75-0.7j}}\right )\right \} \right )\\[3pt] = & \ln (n)^{d-1.01-j}\sum _{q=1}^{\infty } \left (\exp \left \{-\Omega \left(q^{0.4} \ln (n)^{0.036}\right)\right \} + \exp \left \{-\Omega \left(q^{0.7} \ln (n)^{0.043}\right)\right \}\right ) \\[3pt]=& \exp \left\{-\Omega \left(\ln (n)^{0.036}\right)\right\}. \end{align*}
We give a note for the aspects of the proof of bounding
![]() $\mathbb{P}[\mathcal{E}^{(j)+}]$
that are different from the above: use the variable
$\mathbb{P}[\mathcal{E}^{(j)+}]$
that are different from the above: use the variable
![]() $W^{(j)+}_i$
instead of
$W^{(j)+}_i$
instead of
![]() $W^{(j)-}_i$
, events
$W^{(j)-}_i$
, events
![]() $\mathcal{E}^{(j)+}_{\ell }$
instead of
$\mathcal{E}^{(j)+}_{\ell }$
instead of
![]() $\mathcal{E}^{(j)-}_{\ell }$
, and
$\mathcal{E}^{(j)-}_{\ell }$
, and
![]() $\mathcal{H}^{(j)+}_{\ell }$
instead of
$\mathcal{H}^{(j)+}_{\ell }$
instead of
![]() $\mathcal{H}^{(j)-}_{\ell }$
. Define
$\mathcal{H}^{(j)-}_{\ell }$
. Define
![]() $T_{mod}$
instead as
$T_{mod}$
instead as
Finally, use Corollary 4 instead of Corollary 5 (which will be slightly easier to implement).
5. Final phase
We continue our proof by induction of Theorem 8 with our fixed index
![]() $k$
; now we prove the second part. We assume the first part of Theorem 8 to hold, as well as the second part of the Theorem for lesser
$k$
; now we prove the second part. We assume the first part of Theorem 8 to hold, as well as the second part of the Theorem for lesser
![]() $k$
; for example, we have
$k$
; for example, we have
![]() $S^{(k-1)}_{i_{after}(k-1)} = 0$
w.h.p. In this section we focus on the
$S^{(k-1)}_{i_{after}(k-1)} = 0$
w.h.p. In this section we focus on the
![]() $d$
-process for a narrow domain of
$d$
-process for a narrow domain of
![]() $i$
. Let
$i$
. Let
We will consider the
![]() $d$
-process starting at step
$d$
-process starting at step
![]() $i_{before}(k)$
assuming that (16) holds at
$i_{before}(k)$
assuming that (16) holds at
![]() $i = i_{before}(k)$
; we do not need the first part of Theorem 8 in this section otherwise. We do not use martingale arguments here, but rather we show that the distribution of the sequence of time steps at which a vertex of degree
$i = i_{before}(k)$
; we do not need the first part of Theorem 8 in this section otherwise. We do not use martingale arguments here, but rather we show that the distribution of the sequence of time steps at which a vertex of degree
![]() $k$
is chosen from the
$k$
is chosen from the
![]() $d$
-process is similar to a uniform distribution over all possible such sequences. Theorem 8, (10), and (15) tell us that w.h.p. we will have
$d$
-process is similar to a uniform distribution over all possible such sequences. Theorem 8, (10), and (15) tell us that w.h.p. we will have
![]() $\sim \frac{2(d-1)!}{k!}\ln (n)^{0.2}$
vertices of degree at most
$\sim \frac{2(d-1)!}{k!}\ln (n)^{0.2}$
vertices of degree at most
![]() $k$
(or degree equal to
$k$
(or degree equal to
![]() $k$
; they are the same here) left when there are
$k$
; they are the same here) left when there are
![]() $\lfloor \ln (n)^{d-0.8-k} \rfloor$
steps left; hence, the average distance between steps at which we remove vertices of degree
$\lfloor \ln (n)^{d-0.8-k} \rfloor$
steps left; hence, the average distance between steps at which we remove vertices of degree
![]() $k$
is
$k$
is
![]() $\frac{k!}{2(d-1)!} \ln (n)^{d-1-k}$
. When there are this many steps left times
$\frac{k!}{2(d-1)!} \ln (n)^{d-1-k}$
. When there are this many steps left times
![]() $r$
, we expect
$r$
, we expect
![]() $r$
such vertices to remain, and for the probability that there are no vertices of degree
$r$
such vertices to remain, and for the probability that there are no vertices of degree
![]() $k$
to be
$k$
to be
![]() $e^{-r}$
. Most of this section will build towards proving the following Theorem:
$e^{-r}$
. Most of this section will build towards proving the following Theorem:
Theorem 12.
Let
![]() $L(n)$
be an integer-valued function so that
$L(n)$
be an integer-valued function so that
![]() $L(n) = \Theta (\ln (n)^{0.2})$
and let
$L(n) = \Theta (\ln (n)^{0.2})$
and let
![]() $J(n) = \lfloor \frac{dn}{2}\rfloor - i_{before}(k) \sim \ln (n)^{d-0.8-k}$
. Let
$J(n) = \lfloor \frac{dn}{2}\rfloor - i_{before}(k) \sim \ln (n)^{d-0.8-k}$
. Let
![]() $H$
be any graph with
$H$
be any graph with
![]() $i_{before}(k)$
edges which satisfies (
16
) at
$i_{before}(k)$
edges which satisfies (
16
) at
![]() $i = i_{before}(k)$
, has no vertices of degree at most
$i = i_{before}(k)$
, has no vertices of degree at most
![]() $k-1$
, and has
$k-1$
, and has
![]() $L(n)$
vertices of degree
$L(n)$
vertices of degree
![]() $k$
. Also, let
$k$
. Also, let
![]() $r \in{\mathbb{R}}^+$
be arbitrary. Then
$r \in{\mathbb{R}}^+$
be arbitrary. Then
First, we note that, given that (16) holds for
![]() $i = i_{before}(k)$
and by (1), that w.h.p.
$i = i_{before}(k)$
and by (1), that w.h.p.
![]() ${dn - 2i_{before}(k) - S^{(d-1)}_{i_{before}(k)}} = O\left (\frac{dn-2i_{before}}{\ln (n)}\right )$
${dn - 2i_{before}(k) - S^{(d-1)}_{i_{before}(k)}} = O\left (\frac{dn-2i_{before}}{\ln (n)}\right )$
![]() $\Big($
consider
$\Big($
consider
![]() $S^{(d-2)}_{i_{before(k)}}\Big)$
; hence, for all
$S^{(d-2)}_{i_{before(k)}}\Big)$
; hence, for all
![]() $i \in \left[i_{before}(k),i_{after}(k)\right]$
:
$i \in \left[i_{before}(k),i_{after}(k)\right]$
:
Let
![]() $t_{start} = i_{before}(k)$
and
$t_{start} = i_{before}(k)$
and
![]() $t_{end} = \lfloor dn/2 - r J(n)/L(n) \rfloor$
. Consider the
$t_{end} = \lfloor dn/2 - r J(n)/L(n) \rfloor$
. Consider the
![]() $d$
-process between
$d$
-process between
![]() $t_{start}$
and
$t_{start}$
and
![]() $t_{end}$
, given that
$t_{end}$
, given that
![]() $G_{t_{start}} = H$
. At each step two vertices are chosen; now assume that the pair at each step is ordered uniformly at random, so that a sequence of
$G_{t_{start}} = H$
. At each step two vertices are chosen; now assume that the pair at each step is ordered uniformly at random, so that a sequence of
![]() $2(t_{end} - t_{start})$
vertices is generated. We also generate a binary sequence simultaneously, each digit corresponding to a vertex: after a pair of vertices is picked for the vertex sequence, for each of the two vertices (in the order that they are randomly shuffled) append a “1” to the binary sequence if the corresponding vertex had degree
$2(t_{end} - t_{start})$
vertices is generated. We also generate a binary sequence simultaneously, each digit corresponding to a vertex: after a pair of vertices is picked for the vertex sequence, for each of the two vertices (in the order that they are randomly shuffled) append a “1” to the binary sequence if the corresponding vertex had degree
![]() $k$
just before it was picked, and append a “0” otherwise. Let
$k$
just before it was picked, and append a “0” otherwise. Let
![]() $\mathcal{P}: \{0,1\}^{2(t_{end}-t_{start})} \to [0,1]$
be the corresponding probability function that arises from this process (note that, if
$\mathcal{P}: \{0,1\}^{2(t_{end}-t_{start})} \to [0,1]$
be the corresponding probability function that arises from this process (note that, if
![]() $\gamma$
is a string with more than
$\gamma$
is a string with more than
![]() $L(n)$
“1”’s, then
$L(n)$
“1”’s, then
![]() $\mathcal{P}(\gamma )$
= 0). Note that
$\mathcal{P}(\gamma )$
= 0). Note that
![]() $\mathcal{P}$
depends on the graph
$\mathcal{P}$
depends on the graph
![]() $H$
. We compare this to a second probability function
$H$
. We compare this to a second probability function
![]() $\mathcal{Q}: \{0,1\}^{2(t_{end}-t_{start})} \to [0,1]$
, which is defined by picking a binary string with
$\mathcal{Q}: \{0,1\}^{2(t_{end}-t_{start})} \to [0,1]$
, which is defined by picking a binary string with
![]() $L(n)$
1’s and
$L(n)$
1’s and
![]() $2 J(n) - L(n)$
0’s uniformly at random, then taking the first
$2 J(n) - L(n)$
0’s uniformly at random, then taking the first
![]() $2(t_{end} - t_{start})$
digits.
$2(t_{end} - t_{start})$
digits.
For any binary sequence
![]() $\gamma$
with
$\gamma$
with
![]() $\ell$
digits, and
$\ell$
digits, and
![]() $I \subset [\ell ]$
, let
$I \subset [\ell ]$
, let
![]() $\gamma _{I}$
be the subsequence with indices from
$\gamma _{I}$
be the subsequence with indices from
![]() $I$
; for example,
$I$
; for example,
![]() $\gamma _{[a]}$
would be the first
$\gamma _{[a]}$
would be the first
![]() $a$
digits of
$a$
digits of
![]() $\gamma$
, and
$\gamma$
, and
![]() $\gamma _{ \{a\}}$
would just be the
$\gamma _{ \{a\}}$
would just be the
![]() $a$
-th digit (for notation’s sake, let “
$a$
-th digit (for notation’s sake, let “
![]() $\gamma _{[0]}$
” be the empty string). Also let
$\gamma _{[0]}$
” be the empty string). Also let
![]() $\|\gamma \|$
denote the number of 1’s in
$\|\gamma \|$
denote the number of 1’s in
![]() $\gamma$
. We now present the following Lemma:
$\gamma$
. We now present the following Lemma:
Lemma 13.
Let
![]() $\alpha$
be an arbitrary
$\alpha$
be an arbitrary
![]() $2(t_{end} - t_{start})$
length binary sequence with at most
$2(t_{end} - t_{start})$
length binary sequence with at most
![]() $L(n)$
1’s, and let
$L(n)$
1’s, and let
![]() $\gamma$
be the random binary sequence according to either
$\gamma$
be the random binary sequence according to either
![]() $\mathcal{P}$
or
$\mathcal{P}$
or
![]() $\mathcal{Q}$
. Let
$\mathcal{Q}$
. Let
![]() $i \in [2(t_{end} - t_{start})]$
. Then (letting
$i \in [2(t_{end} - t_{start})]$
. Then (letting
![]() $a_{\{0\}} = 1$
for sake of notation):
$a_{\{0\}} = 1$
for sake of notation):
 \begin{equation*} \frac {\mathbb {P}_{\mathcal {P}}[\gamma _{[i]} = \alpha _{[i]} \mid \gamma _{[i-1]} = \alpha _{[i-1]}]}{\mathbb {P}_{\mathcal {Q}}[\gamma _{[i]} = \alpha _{[i]} \mid \gamma _{[i-1]} = \alpha _{[i-1]}]} \begin {cases} = 1 + O\left (\frac {1}{J(n)\ln (n)^{0.39}}\right ) &\text { if } \alpha _{\{i\}} = 0 \text { and } \alpha _{\{i-1\}} = 0 \\[9pt] = 1 + O\left (\frac {\ln (n)^{0.4}}{J(n)}\right ) &\text { if } \alpha _{\{i\}} = 0 \text { and } \alpha _{\{i-1\}} = 1 \\[9pt] = 1 + O\left (\frac {1}{\ln (n)^{0.79}}\right ) &\text { if } \alpha _{\{i\}} = 1 \text { and } \alpha _{\{i-1\}} = 0 \\[9pt] \leq 1 + O\left (\frac {1}{\ln (n)^{0.79}}\right ) &\text { if } \alpha _{\{i\}} = 1 \text { and } \alpha _{\{i-1\}} = 1. \end {cases}\end{equation*}
\begin{equation*} \frac {\mathbb {P}_{\mathcal {P}}[\gamma _{[i]} = \alpha _{[i]} \mid \gamma _{[i-1]} = \alpha _{[i-1]}]}{\mathbb {P}_{\mathcal {Q}}[\gamma _{[i]} = \alpha _{[i]} \mid \gamma _{[i-1]} = \alpha _{[i-1]}]} \begin {cases} = 1 + O\left (\frac {1}{J(n)\ln (n)^{0.39}}\right ) &\text { if } \alpha _{\{i\}} = 0 \text { and } \alpha _{\{i-1\}} = 0 \\[9pt] = 1 + O\left (\frac {\ln (n)^{0.4}}{J(n)}\right ) &\text { if } \alpha _{\{i\}} = 0 \text { and } \alpha _{\{i-1\}} = 1 \\[9pt] = 1 + O\left (\frac {1}{\ln (n)^{0.79}}\right ) &\text { if } \alpha _{\{i\}} = 1 \text { and } \alpha _{\{i-1\}} = 0 \\[9pt] \leq 1 + O\left (\frac {1}{\ln (n)^{0.79}}\right ) &\text { if } \alpha _{\{i\}} = 1 \text { and } \alpha _{\{i-1\}} = 1. \end {cases}\end{equation*}
Proof. First, we consider the cases where
![]() $\alpha _{\{i \}} = 1$
. We have
$\alpha _{\{i \}} = 1$
. We have
For the probability space
![]() $\mathcal{P}$
, we need to consider three subcases: we need to consider whether
$\mathcal{P}$
, we need to consider three subcases: we need to consider whether
![]() $i$
is even or odd, and if it is even, whether
$i$
is even or odd, and if it is even, whether
![]() $\alpha _{ \{i-1\} }$
is 0 or 1, since each step of the
$\alpha _{ \{i-1\} }$
is 0 or 1, since each step of the
![]() $d$
-process outputs two digits of the binary string. Let’s say that
$d$
-process outputs two digits of the binary string. Let’s say that
![]() $\tau$
corresponds to the last step in the
$\tau$
corresponds to the last step in the
![]() $d$
-process before the
$d$
-process before the
![]() $i$
-th binary digit is generated (recall that pairs of digits are generated together). Then if
$i$
-th binary digit is generated (recall that pairs of digits are generated together). Then if
![]() $i$
is odd:
$i$
is odd:
 \begin{align} \mathbb{P}_{\mathcal{P}}[\gamma _{\{i\}} = 1 \mid \gamma _{[i-1]} = \alpha _{[i-1]}] \nonumber &= -\frac{1}{2}\mathbb{E}\left[S^{(k)}_{\tau +1} - S^{(k)}_{\tau } | G_{\tau }\right] \\[2pt]&= \frac{S^{(k)}_{\tau }}{S^{(d-1)}_{\tau }}\left (1 + O\left (\frac{1}{dn-2{\tau }}\right ) \right ) \nonumber \qquad \text{by (3)}\\[2pt]&= \frac{S^{(k)}_{\tau }}{2 \lfloor dn/2-\tau \rfloor }\left (1 + O\left (\frac{1}{\ln (n)^{0.79}}\right )\right ) \nonumber \qquad \text{by (19)} \\[2pt]&= \frac{L(n) - \| \alpha _{[i-1]} \|}{2J(n) - (i-1)}\left (1 + O\left (\frac{1}{\ln (n)^{0.79}}\right )\right ). \end{align}
\begin{align} \mathbb{P}_{\mathcal{P}}[\gamma _{\{i\}} = 1 \mid \gamma _{[i-1]} = \alpha _{[i-1]}] \nonumber &= -\frac{1}{2}\mathbb{E}\left[S^{(k)}_{\tau +1} - S^{(k)}_{\tau } | G_{\tau }\right] \\[2pt]&= \frac{S^{(k)}_{\tau }}{S^{(d-1)}_{\tau }}\left (1 + O\left (\frac{1}{dn-2{\tau }}\right ) \right ) \nonumber \qquad \text{by (3)}\\[2pt]&= \frac{S^{(k)}_{\tau }}{2 \lfloor dn/2-\tau \rfloor }\left (1 + O\left (\frac{1}{\ln (n)^{0.79}}\right )\right ) \nonumber \qquad \text{by (19)} \\[2pt]&= \frac{L(n) - \| \alpha _{[i-1]} \|}{2J(n) - (i-1)}\left (1 + O\left (\frac{1}{\ln (n)^{0.79}}\right )\right ). \end{align}
If
![]() $i$
is even and
$i$
is even and
![]() $\alpha _{ \{i-1\} } = 1$
, then
$\alpha _{ \{i-1\} } = 1$
, then
![]() $S^{(k)}_{\tau } = L(n) - \| \alpha _{[i-1]} \| + 1$
. At step
$S^{(k)}_{\tau } = L(n) - \| \alpha _{[i-1]} \| + 1$
. At step
![]() $\tau$
there are
$\tau$
there are
![]() $S^{(k)}_{\tau } \left(S^{(d-1)}_{\tau } + O(1)\right)$
ordered pairs of vertices whose first vertex has degree
$S^{(k)}_{\tau } \left(S^{(d-1)}_{\tau } + O(1)\right)$
ordered pairs of vertices whose first vertex has degree
![]() $k$
, and at most
$k$
, and at most
![]() $2\binom{S^{(k)}_{\tau }}{2}$
ordered pairs of vertices both with degree
$2\binom{S^{(k)}_{\tau }}{2}$
ordered pairs of vertices both with degree
![]() $k$
; hence:
$k$
; hence:
 \begin{align} \mathbb{P}_{\mathcal{P}}[\gamma _{\{i\}} = 1 \nonumber \mid \gamma _{[i-1]} = \alpha _{[i-1]}] &\leq \frac{S^{(k)}_{\tau } - 1}{S^{(d-1)}_{\tau } + O(1)}\\[4pt]&= \frac{S^{(k)}_{\tau } - 1}{2 \lfloor dn/2-\tau \rfloor }\left (1 + O\left (\frac{1}{\ln (n)^{0.79}}\right )\right ) \qquad \text{by (19)} \nonumber \\[4pt]&= \frac{L(n) - \| \alpha _{[i-1]} \|}{2J(n) - (i-1)}\left (1 + O\left (\frac{1}{\ln (n)^{0.79}}\right )\right ). \end{align}
\begin{align} \mathbb{P}_{\mathcal{P}}[\gamma _{\{i\}} = 1 \nonumber \mid \gamma _{[i-1]} = \alpha _{[i-1]}] &\leq \frac{S^{(k)}_{\tau } - 1}{S^{(d-1)}_{\tau } + O(1)}\\[4pt]&= \frac{S^{(k)}_{\tau } - 1}{2 \lfloor dn/2-\tau \rfloor }\left (1 + O\left (\frac{1}{\ln (n)^{0.79}}\right )\right ) \qquad \text{by (19)} \nonumber \\[4pt]&= \frac{L(n) - \| \alpha _{[i-1]} \|}{2J(n) - (i-1)}\left (1 + O\left (\frac{1}{\ln (n)^{0.79}}\right )\right ). \end{align}
Hence the final inequality of the Lemma holds by (21) and (22).
Next, consider the case where
![]() $i$
is even and
$i$
is even and
![]() $\alpha _{ \{i-1\} } = 0$
; here,
$\alpha _{ \{i-1\} } = 0$
; here,
![]() $S^{(k)}_{\tau } = L(n) - \| \alpha _{[i-1]} \|$
once again. At step
$S^{(k)}_{\tau } = L(n) - \| \alpha _{[i-1]} \|$
once again. At step
![]() $\tau$
there are
$\tau$
there are
![]() $\left(S^{(d-1)}_{\tau } - S^{(k)}_{\tau }\right) \left(S^{(d-1)}_{\tau } + O(1)\right)$
ordered pairs of vertices whose first vertex has degree greater than
$\left(S^{(d-1)}_{\tau } - S^{(k)}_{\tau }\right) \left(S^{(d-1)}_{\tau } + O(1)\right)$
ordered pairs of vertices whose first vertex has degree greater than
![]() $k$
, and
$k$
, and
![]() $S^{(k)}_{\tau } \left(S^{(d-1)}_{\tau } - S^{(k)}_{\tau } + O(1)\right)$
ordered pairs of vertices for which the first vertex has degree greater
$S^{(k)}_{\tau } \left(S^{(d-1)}_{\tau } - S^{(k)}_{\tau } + O(1)\right)$
ordered pairs of vertices for which the first vertex has degree greater
![]() $k$
and the second vertex has degree
$k$
and the second vertex has degree
![]() $k$
(one can “pick the second vertex first” to see this). Hence:
$k$
(one can “pick the second vertex first” to see this). Hence:
 \begin{align} \mathbb{P}_{\mathcal{P}}[\gamma _{\{i\}} = 1 \nonumber \mid \gamma _{[i-1]} = \alpha _{[i-1]}] &= \frac{S^{(k)}_{\tau } }{S^{(d-1)}_{\tau }} \left (1 + O \left (\frac{1}{S^{(d-1)}_{\tau }}\right )\right ) \qquad \text{since}\ S^{(d-1)}_{\tau } \gg S^{(k)}_{\tau } \text{ there} \\[4pt]&= \frac{S^{(k)}_{\tau } }{2 \lfloor dn/2-\tau \rfloor } \left (1 + O \left (\frac{1}{\ln (n)^{0.79}}\right )\right ) \nonumber \qquad \text{by (19)} \\[4pt]&= \frac{L(n) - \| \alpha _{[i-1]} \|}{2J(n) - (i-1)}\left (1 + O\left (\frac{1}{\ln (n)^{0.79}}\right )\right ), \end{align}
\begin{align} \mathbb{P}_{\mathcal{P}}[\gamma _{\{i\}} = 1 \nonumber \mid \gamma _{[i-1]} = \alpha _{[i-1]}] &= \frac{S^{(k)}_{\tau } }{S^{(d-1)}_{\tau }} \left (1 + O \left (\frac{1}{S^{(d-1)}_{\tau }}\right )\right ) \qquad \text{since}\ S^{(d-1)}_{\tau } \gg S^{(k)}_{\tau } \text{ there} \\[4pt]&= \frac{S^{(k)}_{\tau } }{2 \lfloor dn/2-\tau \rfloor } \left (1 + O \left (\frac{1}{\ln (n)^{0.79}}\right )\right ) \nonumber \qquad \text{by (19)} \\[4pt]&= \frac{L(n) - \| \alpha _{[i-1]} \|}{2J(n) - (i-1)}\left (1 + O\left (\frac{1}{\ln (n)^{0.79}}\right )\right ), \end{align}
hence the third equality of the Lemma holds by (21) and (23).
Now consider
![]() $\alpha _{\{i\}} = 0$
. By modifying (20) to accommodate
$\alpha _{\{i\}} = 0$
. By modifying (20) to accommodate
![]() $\gamma _{\{i\}} = 0$
, we have
$\gamma _{\{i\}} = 0$
, we have
Similarly, by modifying (21) and (23), if
![]() $a_{\{i-1\}} = 0$
then
$a_{\{i-1\}} = 0$
then
By modifying (21) and (22), if
![]() $a_{\{i-1\}} = 1$
, then
$a_{\{i-1\}} = 1$
, then
 \begin{align} \mathbb{P}_{\mathcal{P}}[\gamma _{\{i\}} = 0 \mid \gamma _{[i-1]} = \alpha _{[i-1]}] & \geq 1 - \frac{L(n) - \| \alpha _{[i-1]} \|}{2J(n) - (i-1)}\left (1 + O\left (\frac{1}{\ln (n)^{0.79}}\right )\right ) \nonumber \\[4pt]&= 1 + O\left (\frac{L(n) - \| \alpha _{[i-1]} \|}{2J(n) - (i-1)}\right ). \end{align}
\begin{align} \mathbb{P}_{\mathcal{P}}[\gamma _{\{i\}} = 0 \mid \gamma _{[i-1]} = \alpha _{[i-1]}] & \geq 1 - \frac{L(n) - \| \alpha _{[i-1]} \|}{2J(n) - (i-1)}\left (1 + O\left (\frac{1}{\ln (n)^{0.79}}\right )\right ) \nonumber \\[4pt]&= 1 + O\left (\frac{L(n) - \| \alpha _{[i-1]} \|}{2J(n) - (i-1)}\right ). \end{align}
Since
![]() $L(n) = \Theta (\ln (n)^{0.2})$
and
$L(n) = \Theta (\ln (n)^{0.2})$
and
then
![]() $\frac{L(n) - \| \alpha _{[i-1]} \|}{2J(n) - (i-1)} = O\left (\frac{\ln (n)^{0.4}}{J(n)}\right )$
. Therefore the ratio of (25) and (24) is
$\frac{L(n) - \| \alpha _{[i-1]} \|}{2J(n) - (i-1)} = O\left (\frac{\ln (n)^{0.4}}{J(n)}\right )$
. Therefore the ratio of (25) and (24) is
![]() $1 + O \left (\frac{1}{J(n) \ln (n)^{0.39}}\right )$
, verifying the first inequality of the Lemma, and the ratio of (26) and (24) is
$1 + O \left (\frac{1}{J(n) \ln (n)^{0.39}}\right )$
, verifying the first inequality of the Lemma, and the ratio of (26) and (24) is
![]() $1 + O \left (\frac{\ln (n)^{0.4}}{J(n)}\right )$
, verifying the second inequality of the Lemma.
$1 + O \left (\frac{\ln (n)^{0.4}}{J(n)}\right )$
, verifying the second inequality of the Lemma.
Proof of Theorem
12. First, let
![]() $\alpha$
be an arbitrary string which satisfies the criteria in Lemma 13. By using the Lemma 13 recursively:
$\alpha$
be an arbitrary string which satisfies the criteria in Lemma 13. By using the Lemma 13 recursively:
 \begin{align} \frac{\mathbb{P}_{\mathcal{P}}[\gamma = \alpha ]}{\mathbb{P}_{\mathcal{Q}}[\gamma = \alpha ]} &\leq \exp \left \{ O\left (J(n) \frac{1}{J(n) \ln (n)^{0.39}} + L(n) \left (\frac{1}{\ln (n)^{0.79}} + \frac{\ln (n)^{0.4}}{J(n)}\right )\right ) \right \}\nonumber \\[4pt]&= 1 + o(1), \end{align}
\begin{align} \frac{\mathbb{P}_{\mathcal{P}}[\gamma = \alpha ]}{\mathbb{P}_{\mathcal{Q}}[\gamma = \alpha ]} &\leq \exp \left \{ O\left (J(n) \frac{1}{J(n) \ln (n)^{0.39}} + L(n) \left (\frac{1}{\ln (n)^{0.79}} + \frac{\ln (n)^{0.4}}{J(n)}\right )\right ) \right \}\nonumber \\[4pt]&= 1 + o(1), \end{align}
and if
![]() $\alpha$
is an arbitrary string with no two consecutive 1’s which satisfies the criteria in Lemma 13, then by similar logic,
$\alpha$
is an arbitrary string with no two consecutive 1’s which satisfies the criteria in Lemma 13, then by similar logic,
Let
![]() $\mathcal{C}$
be the event that
$\mathcal{C}$
be the event that
![]() $\gamma$
has two consecutive 1’s; we consider
$\gamma$
has two consecutive 1’s; we consider
![]() $\mathbb{P}[ \, \mathcal{C} \mid G_{t_{start}} = H]$
. We consider probability space
$\mathbb{P}[ \, \mathcal{C} \mid G_{t_{start}} = H]$
. We consider probability space
![]() $\mathcal{Q}$
first. Recall that
$\mathcal{Q}$
first. Recall that
![]() $\alpha$
is a string that has
$\alpha$
is a string that has
![]() $\sim 2J(n) = \Omega (\ln (n)^{1.2})$
characters and at most
$\sim 2J(n) = \Omega (\ln (n)^{1.2})$
characters and at most
![]() $L(n) = \Theta (\ln (n)^{0.2})$
1’s. Because
$L(n) = \Theta (\ln (n)^{0.2})$
1’s. Because
![]() $\mathcal{Q}$
is a truncation of a uniform distribution, the probability of having two consecutive 1’s will be
$\mathcal{Q}$
is a truncation of a uniform distribution, the probability of having two consecutive 1’s will be
![]() $O\left (\frac{(L(n))^2}{J(n)}\right ) = O(\ln (n)^{-0.8})$
. Hence, by (27) we must have
$O\left (\frac{(L(n))^2}{J(n)}\right ) = O(\ln (n)^{-0.8})$
. Hence, by (27) we must have
We now combine (28) and (29) to prove Theorem 12 (for ease of notation, assume we are given
![]() $G_{t_{start}} = H$
):
$G_{t_{start}} = H$
):
 \begin{align*} \mathbb{P}\left [S^{(k)}_{\lfloor \frac{dn}{2} - \frac{r J(n)}{L(n)} \rfloor } = 0 \right ] &= \mathbb{P}_{\mathcal{P}}[\|\gamma \| = L(n)] \\[4pt]&= \mathbb{P}_{\mathcal{P}}[\|\gamma \| = L(n) \ | \ \mathcal{C}]\mathbb{P}_{\mathcal{P}}[\mathcal{C}] + \mathbb{P}_{\mathcal{P}}[\|\gamma \| = L(n) \ | \ \overline{\mathcal{C}}]\mathbb{P}_{\mathcal{P}}[\overline{\mathcal{C}}] \\[4pt]&= \mathbb{P}_{\mathcal{Q}}[||\gamma || = L(n)] + o(1) \qquad \text{by (28) and (29)}\\[4pt]&= \frac{\binom{2(t_{end}-t_{start})}{L(n)}}{\binom{2J(n)}{L(n)}} + o(1) \\[4pt]&= \frac{\binom{2J(n) - 2(\lfloor r J(n)/L(n) \rfloor )}{L(n)}}{\binom{2J(n)}{L(n)}} + o(1) \\[4pt]&= \left (1-\frac{r(1+ o(1))}{L(n)}\right )^{L(n)} + o(1) \\[4pt]& = e^{-r} + o(1). \end{align*}
\begin{align*} \mathbb{P}\left [S^{(k)}_{\lfloor \frac{dn}{2} - \frac{r J(n)}{L(n)} \rfloor } = 0 \right ] &= \mathbb{P}_{\mathcal{P}}[\|\gamma \| = L(n)] \\[4pt]&= \mathbb{P}_{\mathcal{P}}[\|\gamma \| = L(n) \ | \ \mathcal{C}]\mathbb{P}_{\mathcal{P}}[\mathcal{C}] + \mathbb{P}_{\mathcal{P}}[\|\gamma \| = L(n) \ | \ \overline{\mathcal{C}}]\mathbb{P}_{\mathcal{P}}[\overline{\mathcal{C}}] \\[4pt]&= \mathbb{P}_{\mathcal{Q}}[||\gamma || = L(n)] + o(1) \qquad \text{by (28) and (29)}\\[4pt]&= \frac{\binom{2(t_{end}-t_{start})}{L(n)}}{\binom{2J(n)}{L(n)}} + o(1) \\[4pt]&= \frac{\binom{2J(n) - 2(\lfloor r J(n)/L(n) \rfloor )}{L(n)}}{\binom{2J(n)}{L(n)}} + o(1) \\[4pt]&= \left (1-\frac{r(1+ o(1))}{L(n)}\right )^{L(n)} + o(1) \\[4pt]& = e^{-r} + o(1). \end{align*}
We can now complete the proof of the second statement of Theorem 8 at value
![]() $k$
. Roughly speaking, we will use Theorem 12 with
$k$
. Roughly speaking, we will use Theorem 12 with
![]() $L(n) \approx \frac{2(d-1)! \ln (n)^{0.2}}{k!}$
, so
$L(n) \approx \frac{2(d-1)! \ln (n)^{0.2}}{k!}$
, so
![]() $\frac{dn}{2} - i(r_{k},k) \approx \frac{r_k J(n)}{L(n)}.$
First, note that
$\frac{dn}{2} - i(r_{k},k) \approx \frac{r_k J(n)}{L(n)}.$
First, note that
![]() $S^{(k)}_{i_{after}(k)} = 0$
(w.h.p.) comes automatically when the rest of the statement is proved (by putting
$S^{(k)}_{i_{after}(k)} = 0$
(w.h.p.) comes automatically when the rest of the statement is proved (by putting
![]() $r_{\ell } = 0$
for
$r_{\ell } = 0$
for
![]() $\ell \lt k$
and having
$\ell \lt k$
and having
![]() $r_k \to 0$
). Let
$r_k \to 0$
). Let
![]() $\mathcal{G}_{\ell }$
be the event that
$\mathcal{G}_{\ell }$
be the event that
![]() $S^{(\ell )}_{ \lfloor i(r_{\ell },\ell )\rfloor } = 0$
and
$S^{(\ell )}_{ \lfloor i(r_{\ell },\ell )\rfloor } = 0$
and
![]() $\mathcal{G} = \bigcap _{\ell \leq k} \mathcal{G}_{\ell }$
, let
$\mathcal{G} = \bigcap _{\ell \leq k} \mathcal{G}_{\ell }$
, let
![]() $\mathcal{F}$
be the event that (16) holds for
$\mathcal{F}$
be the event that (16) holds for
![]() $i = i_{before}(k)$
and
$i = i_{before}(k)$
and
![]() $S^{(j)}_{i_{before(k)}} = 0$
for
$S^{(j)}_{i_{before(k)}} = 0$
for
![]() $j \lt k$
, and let
$j \lt k$
, and let
![]() $\mathcal{A} = \mathcal{F} \cap \bigcap _{\ell \lt k} \mathcal{G}_{\ell }$
. Also, let
$\mathcal{A} = \mathcal{F} \cap \bigcap _{\ell \lt k} \mathcal{G}_{\ell }$
. Also, let
Note that, by part 1 of Theorem 8, by induction on the second part Theorem 8, and since
![]() $i_{before}(k) \gt i_{after}(k-1)$
,
$i_{before}(k) \gt i_{after}(k-1)$
,
![]() $\mathcal{F}$
happens with probability
$\mathcal{F}$
happens with probability
![]() $1 - o(1)$
. Therefore:
$1 - o(1)$
. Therefore:
 \begin{align*} \mathbb{P}[\mathcal{G}] &= \mathbb{P}\left [\mathcal{G}_{k} \cap \mathcal{A} \right ] + o(1)\\[5pt]&= \sum _{p \in \mathcal{I}} \mathbb{P}\left [\mathcal{G} \ \bigg | \ \mathcal{A} \cap \left(S^{(k)}_{i_{before}(k)} = p\right) \right ] \mathbb{P}\left [\mathcal{A} \cap \left(S^{(k)}_{i_{before}(k)} = p\right) \right ] + o(1). \end{align*}
\begin{align*} \mathbb{P}[\mathcal{G}] &= \mathbb{P}\left [\mathcal{G}_{k} \cap \mathcal{A} \right ] + o(1)\\[5pt]&= \sum _{p \in \mathcal{I}} \mathbb{P}\left [\mathcal{G} \ \bigg | \ \mathcal{A} \cap \left(S^{(k)}_{i_{before}(k)} = p\right) \right ] \mathbb{P}\left [\mathcal{A} \cap \left(S^{(k)}_{i_{before}(k)} = p\right) \right ] + o(1). \end{align*}
We can now apply (10), (15), and Theorem 12 to get
for
![]() $p \in \mathcal{I}$
. We note that all
$p \in \mathcal{I}$
. We note that all
![]() $o(1)$
functions in the sum can be made to be the same by carefully reviewing the proof of Theorem 12. Therefore:
$o(1)$
functions in the sum can be made to be the same by carefully reviewing the proof of Theorem 12. Therefore:
 \begin{align*} \mathbb{P}[\mathcal{G}] &= \sum _{p \in \mathcal{I}} (e^{-r_{\ell }} + o(1)) \mathbb{P}\left [\mathcal{A} \cap \left(S^{(k)}_{i_{before}(k)} = p\right) \right ] +o(1) \qquad \\&= e^{-r_{\ell }} \sum _{p \in \mathcal{I}}\mathbb{P}\left [\mathcal{A} \cap \left(S^{(k)}_{i_{before}(k)} = p\right) \right ] + o(1) \\&= e^{-r_{\ell }} \mathbb{P}\left [\bigcap _{\ell \lt k} \mathcal{G}_{\ell }\right ] + o(1) \qquad \text{by Theorem 8} \\&= \exp \left \{ \sum _{\ell = 0}^{k} e^{- r_{\ell }} \right \} + o(1) \qquad \text{by induction on Theorem 8,} \end{align*}
\begin{align*} \mathbb{P}[\mathcal{G}] &= \sum _{p \in \mathcal{I}} (e^{-r_{\ell }} + o(1)) \mathbb{P}\left [\mathcal{A} \cap \left(S^{(k)}_{i_{before}(k)} = p\right) \right ] +o(1) \qquad \\&= e^{-r_{\ell }} \sum _{p \in \mathcal{I}}\mathbb{P}\left [\mathcal{A} \cap \left(S^{(k)}_{i_{before}(k)} = p\right) \right ] + o(1) \\&= e^{-r_{\ell }} \mathbb{P}\left [\bigcap _{\ell \lt k} \mathcal{G}_{\ell }\right ] + o(1) \qquad \text{by Theorem 8} \\&= \exp \left \{ \sum _{\ell = 0}^{k} e^{- r_{\ell }} \right \} + o(1) \qquad \text{by induction on Theorem 8,} \end{align*}
proving Theorem 8.
Acknowledgements
Thanks to my advisor Tom Bohman, who gave me much guidance and input, and to the National Science Foundation for its financial support. Competing interests: The author declares none.