Hostname: page-component-5cf477f64f-54txb Total loading time: 0 Render date: 2025-04-04T07:26:11.884Z Has data issue: false hasContentIssue false
  • English
  • Français

B2[g] Sets and a Conjecture of Schinzel and Schmidt

Published online by Cambridge University Press:  01 November 2008

JAVIER CILLERUELO  and
CARLOS VINUESA
JAVIER CILLERUELO
Affiliation:
Departamento de Matemáticas, Universidad Autónoma de Madrid, 28049-Madrid, Spain (e-mail: [email protected], [email protected])
CARLOS VINUESA
Affiliation:
Departamento de Matemáticas, Universidad Autónoma de Madrid, 28049-Madrid, Spain (e-mail: [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

A set of integers 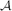is called a B2[g] set if every integer m has at most g representations of the form m = a + a′, with a ≤ a′ and a, a′ ∈ 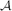. We obtain a new lower bound for F(g, n), the largest cardinality of a B2[g] set in {1,. . .,n}. More precisely, we prove that infn→∞ 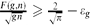where ϵg → 0 when g → ∞. We show a connection between this problem and another one discussed by Schinzel and Schmidt, which can be considered its continuous version.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 17 , Issue 6 , November 2008 , pp. 741 - 747
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Cilleruelo, J., Ruzsa, I. and Trujillo, C. (2002) Upper and lower bounds for finite B 2[g] sequences. J. Number Theory 97 26–34.CrossRefGoogle Scholar
[2]Green, B. (2001) The number of squares and B h[g] sequences. Acta Arithmetica 100 365–390.CrossRefGoogle Scholar
[3]Kolountzakis, M. (1996) The density of B h[g] sequences and the minimum of dense cosine sums. J. Number Theory 56 4–11.CrossRefGoogle Scholar
[4]Martin, G. and O'Bryant, K. (2006) Constructions of generalized Sidon sets. J. Combin. Theory Ser. A 113 591–607.CrossRefGoogle Scholar
[5]Martin, G. and O'Bryant, K. (2007) The symmetric subset problem in continuous Ramsey theory. Experiment. Math. 16 145–166.CrossRefGoogle Scholar
[6]Ruzsa, I. (1993) Solving a linear equation in a set of integers I. Acta Arithmetica 65 259–282.CrossRefGoogle Scholar
[7]Schinzel, A. and Schmidt, W. M. (2002) Comparison of L 1- and L ∞-norms of squares of polynomials. Acta Arithmetica 104 283–296.CrossRefGoogle Scholar
[8]Tao, T. and Vu, V. (2006) Additive Combinatorics, Vol. 105 of Cambridge Studies in Advanced Mathematics, Cambridge University Press.CrossRefGoogle Scholar
[9]Yu, G. (2007) An upper bound for B 2[g] sets. J. Number Theory 122 211–220.CrossRefGoogle Scholar