Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T06:13:02.176Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotics for the number of standard tableaux of skew shape and for weighted lozenge tilings

Part of: Designs and configurations Combinatorics

Published online by Cambridge University Press:  18 October 2021

Alejandro H. Morales ,
Igor Pak  and
Martin Tassy
Alejandro H. Morales*
Affiliation:
Department of Mathematics and Statistics, UMass, Amherst, MA
Igor Pak
Affiliation:
Department of Mathematics, University of California, Los Angeles, CA
Martin Tassy
Affiliation:
Department of Mathematics, Dartmouth College, Hanover, NH
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove and generalise a conjecture in [MPP4] about the asymptotics of 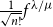$\frac{1}{\sqrt{n!}} f^{\lambda/\mu}$ , where 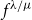$f^{\lambda/\mu}$ is the number of standard Young tableaux of skew shape 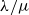$\lambda/\mu$ which have stable limit shape under the 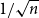$1/\sqrt{n}$ scaling. The proof is based on the variational principle on the partition function of certain weighted lozenge tilings.

Keywords

standard tableauxskew shapesasymptoticsEuler numberslozenge tilingsvariational principleNaruse hook length formula

MSC classification

Primary: 05A16: Asymptotic enumeration
Secondary: 05B45: Tessellation and tiling problems 05A20: Combinatorial inequalities 05A10: Factorials, binomial coefficients, combinatorial functions
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 4 , July 2022 , pp. 550 - 573
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adin, R. and Roichman, Y., Standard Young tableaux, in Handbook of enumerative combinatorics, CRC Press, Boca Raton, FL, 2015, 895–974.Google Scholar
Angel, O., Holroyd, A. E., Romik, D. and Virág, B., Random sorting networks, Adv. Math. 215 (2007), 839–868.CrossRefGoogle Scholar
Askey, R. A. and Roy, R., Barnes G-function, in NIST Handbook of Mathematical Functions (Olver, F. W. J. et al., eds.), Cambridge Univ. Press, 2012.Google Scholar
Betea, D., Elliptic Combinatorics and Markov Processes, Ph.D. thesis, Caltech, 2012, 116 pp.; available at https://tinyurl.com/yy37sjvb Google Scholar
Borodin, A., Gorin, V. and Rains, E. M., q-distributions on boxed plane partitions, Selecta Math. 16 (2010), 731–789.CrossRefGoogle Scholar
Chandgotia, N., Pak, I. and Tassy, M., Kirszbraun–type theorems for graphs, J. Combin. Theory, Ser. B 137 (2019), 10–24.Google Scholar
Cohn, H., Elkies, N. and Propp, J., Local statistics for random domino tilings of the Aztec diamond, Duke Math. J. 85 (1996), 117–166.CrossRefGoogle Scholar
Cohn, H., Kenyon, R. and Propp, J., A variational principle for domino tilings. J. AMS 14 (2001), 297–346.Google Scholar
Dauvergne, D., The Archimedean limit of random sorting networks, preprint (2018), 61 pp.; arXiv: 1802.08934.Google Scholar
Dimitrov, E. and Knizel, A., Log-gases on quadratic lattices via discrete loop equations and q-boxed plane partitions, J. Funct. Anal. 276 (2019), 3067–3169.CrossRefGoogle Scholar
Dousse, J. and Féray, V., Asymptotics for skew standard Young tableaux via bounds for characters, Proc. AMS 147 (2019), 4189–4203.CrossRefGoogle Scholar
Feit, W., The degree formula for the skew-representations of the symmetric group, Proc. AMS 4 (1953), 740–744.CrossRefGoogle Scholar
Féray, V. and Śniady, P., Asymptotics of characters of symmetric groups related to Stanley character formula, Ann. of Math. 173 (2011), 887–906.CrossRefGoogle Scholar
Gordenko, A., Limit shapes of large skew Young tableaux and a modification of the TASEP process, preprint (2020), 43 pp.; arXiv:2009.10480.Google Scholar
Kenyon, R., Lectures on dimers, in Statistical mechanics, AMS, Providence, RI, 2009, 191–230.CrossRefGoogle Scholar
Konvalinka, M., A bijective proof of the hook-length formula for skew shapes, European J. Combin. 88 (2020), 103104, 14 pp.CrossRefGoogle Scholar
Menz, G. and Tassy, M., A variational principle for a non-integrable model, Probab. Theory Related Fields 177 (2020), 747–822.CrossRefGoogle Scholar
Morales, A. H., Pak, I. and Panova, G., Hook formulas for skew shapes I. q-analogues and bijections, J. Combin. Theory, Ser. A 154 (2018), 350–405.Google Scholar
Morales, A. H., Pak, I. and Panova, G., Hook formulas for skew shapes II. Combinatorial proofs and enumerative applications, SIAM Jour. Discrete Math. 31 (2017), 1953–1989.CrossRefGoogle Scholar
Morales, A. H., Pak, I. and Panova, G., Hook formulas for skew shapes III. Multivariate and product formulas, Algebraic Combinatorics 2 (2019), 815–861.CrossRefGoogle Scholar
Morales, A. H., Pak, I. and Panova, G., Asymptotics of the number of standard Young tableaux of skew shape, European J. Combin 70 (2018), 26–49.CrossRefGoogle Scholar
Morales, A. H., and Zhu, D. G., On the Okounkov-Olshanski formula for standard tableaux of skew shapes, preprint (2020), 37 pp.; arXiv:2007.05006Google Scholar
Naruse, H., Schubert calculus and hook formula, talk slides at 73rd Sém. Lothar. Combin., Strobl, Austria, 2014; available at https://tinyurl.com/y5zunwk4 Google Scholar
Naruse, H. and Okada, S., Skew hook formula for d-complete posets, Algebraic Combinatorics 2 (2019), 541–571.CrossRefGoogle Scholar
Pak, I., Complexity problems in enumerative combinatorics, in Proc. ICM Rio de Janeiro, Vol. IV. Invited lectures, World Sci., Hackensack, NJ, 2018, 3153–3180; expanded version available at arXiv:1803.06636.Google Scholar
Pak, I., Skew shape asymptotics, a case-based introduction, Sém. Lothar. Combin. 84 (2021), Article B84a.Google Scholar
Pak, I., Sheffer, A., and Tassy, M., Fast domino tileability, Discrete Comput. Geom. 56 (2016), 377–394.CrossRefGoogle Scholar
Pittel, B. and Romik, D., Limit shapes for random square Young tableaux, Adv. Appl. Math. 38 (2007), 164–209.CrossRefGoogle Scholar
Romik, D., The surprising mathematics of longest increasing subsequences, Cambridge Univ. Press, New York, 2015.CrossRefGoogle Scholar
Stanley, R. P., On the enumeration of skew Young tableaux, Adv. Appl. Math. 30 (2003), 283–294.CrossRefGoogle Scholar
Stanley, R. P., Enumerative Combinatorics, vol. 1 and 2, Cambridge Univ. Press, 2012 and 1999.CrossRefGoogle Scholar
Sun, W., Dimer model, bead and standard Young tableaux: finite cases and limit shapes, preprint (2018), 67 pp. ; arXiv:1804.03414.Google Scholar
Thurston, W. P., Groups, tilings and finite state automata, in Lecture Notes, AMS Summer Meetings, Bolder, CO, 1989, 51 pp.; available at https://tinyurl.com/y62mzl4r Google Scholar
Thurston, W. P. and Milnor, J. W., The geometry and topology of three-manifolds, Princeton Univ. Press, Princeton, NJ, 1979.Google Scholar
Wachs, M., Flagged Schur functions, Schubert polynomials, and symmetrizing operators, J. Combin. Theory, Ser. A 40 (1985), 276–289.CrossRefGoogle Scholar