Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-28T17:05:42.228Z Has data issue: false hasContentIssue false
  • English
  • Français

An Approximation by Lacunary Sequence of Vectors

Published online by Cambridge University Press:  01 May 2008

ARTŪRAS DUBICKAS
ARTŪRAS DUBICKAS*
Affiliation:
Department of Mathematics and Informatics, Vilnius University, Naugarduko 24, Vilnius LT-03225, Lithuania; Institute of Mathematics and Informatics, Akademijos 4, LT-08663 Vilnius, Lithuania (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 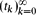be a sequence of real numbers satisfying 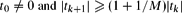for each k ≥ 0, where M ≥ 1 is a fixed number. We prove that, for any sequence of real numbers 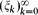, there is a real number ξ such that 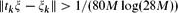for each k ≥ 0. Here, 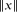denotes the distance from 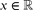to the nearest integer. This is a corollary derived from our main theorem, which is a more general matrix version of this statement with explicit constants.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 17 , Issue 3 , May 2008 , pp. 339 - 345
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Akhunzhanov, R. K. and Moshchevitin, N. G. (2004) On the chromatic number of a distance graph associated with a lacunary sequence. Dokl. Ross. Akad. Nauk 397 295–296 (in Russian).Google Scholar
[2]Akhunzhanov, R. K. and Moshchevitin, N. G. (2005) Density modulo 1 of sublacunary sequences. Math. Notes 77 741–750.CrossRefGoogle Scholar
[3]Alon, N. and Spencer, J. (1992) The Probabilistic Method, Wiley, New York.Google Scholar
[4]Dubickas, A. (2006) Arithmetical properties of powers of algebraic numbers. Bull. London Math. Soc. 38 70–80.CrossRefGoogle Scholar
[5]Dubickas, A. (2006) On the fractional parts of lacunary sequences. Math. Scand. 99 136–146.CrossRefGoogle Scholar
[6]Dubickas, A. An approximation property of lacunary sequences. Israel J. Math., to appear.Google Scholar
[7]Dubickas, A. On the distribution of powers of a complex number. Submitted.Google Scholar
[8]Erdős, P. (1975) Problems and results on Diophantine approximations II. In Repartition Modulo 1, Actes Colloq. Marseille–Luminy 1974, Vol. 475 of Lecture Notes in Mathematics, Springer, pp. 89–99.Google Scholar
[9]Flatto, L., Lagarias, J. C. and Pollington, A. D. (1995) On the range of fractional parts {ξ(p/q)n}. Acta Arith. 70 125–147.CrossRefGoogle Scholar
[10]Katznelson, Y. (2001) Chromatic numbers of Cayley graphs on ℤ and recurrence. Combinatorica 21 211–219.CrossRefGoogle Scholar
[11]Khintchine, A. (1926) Über eine Klasse linearer diophantischer Approximationen. Rend. Circ. Mat. Palermo 50 170–195.CrossRefGoogle Scholar
[12]deMathan, B. Mathan, B. (1980) Numbers contravening a condition in density modulo 1. Acta Math. Acad. Sci. Hung. 36 237–241.Google Scholar
[13]Moschchevitin, N. G. (2007) A version of the proof for Peres–Schlag's theorem on lacunary sequences. Preprint: arXiv:0708.2087.Google Scholar
[14]Peres, Y. and Schlag, W. (2007) Two Erdős problems on lacunary sequences: Chromatic number and Diophantine approximation. Preprint: arXiv:0706.0223.Google Scholar
[15]Pollington, A. D. (1979) On the density of the sequence {n k ξ}. Illinois J. Math. 23 511–515.CrossRefGoogle Scholar
[16]Weyl, H. (1916) Über die Gleichverteilung von Zahlen modulo Eins. Math. Ann. 77 313–352.CrossRefGoogle Scholar