Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
2009.
Combinatorial Number Theory and Additive Group Theory.
p.
57.
Hamidoune, Y.O.
2010.
Extensions of the Scherk–Kemperman Theorem.
Journal of Combinatorial Theory, Series A,
Vol. 117,
Issue. 7,
p.
974.
Grynkiewicz, David J.
Marchan, Luz Elimar
and
Ordaz, Oscar
2012.
A weighted generalization of two theorems of Gao.
The Ramanujan Journal,
Vol. 28,
Issue. 3,
p.
323.
Fan, Yushuang
Gao, Weidong
Wang, Linlin
and
Zhong, Qinghai
2013.
Two zero-sum invariants on finite abelian groups.
European Journal of Combinatorics,
Vol. 34,
Issue. 8,
p.
1331.
Plagne, Alain
Serra, Oriol
and
Zémor, Gilles
2013.
Yahya Ould Hamidoune’s mathematical journey: A critical review of his work.
European Journal of Combinatorics,
Vol. 34,
Issue. 8,
p.
1207.
Gao, Weidong
Han, Dongchun
Peng, Jiangtao
and
Sun, Fang
2014.
On zero-sum subsequences of lengthkexp(G).
Journal of Combinatorial Theory, Series A,
Vol. 125,
Issue. ,
p.
240.
Han, Dongchun
and
Zhang, Hanbin
2018.
On zero-sum subsequences of prescribed length.
International Journal of Number Theory,
Vol. 14,
Issue. 01,
p.
167.
Gao, Weidong
Hong, Siao
and
Peng, Jiangtao
2022.
On zero-sum subsequences of length kexp(G) II.
Journal of Combinatorial Theory, Series A,
Vol. 187,
Issue. ,
p.
105563.
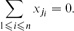
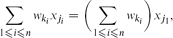 where xj1 is the most repeated value in x. For w = (1, . . ., 1), this result reduces to Gao's theorem.
where xj1 is the most repeated value in x. For w = (1, . . ., 1), this result reduces to Gao's theorem.