Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ge, Gennian
Jing, Yifan
Xu, Zixiang
and
Zhang, Tao
2020.
Color Isomorphic Even Cycles and a Related Ramsey Problem.
SIAM Journal on Discrete Mathematics,
Vol. 34,
Issue. 3,
p.
1999.
Balla, Igor
Letzter, Shoham
and
Sudakov, Benny
2020.
Orthonormal Representations of H-Free Graphs.
Discrete & Computational Geometry,
Vol. 64,
Issue. 3,
p.
654.
Zhai, Mingqing
Fang, Longfei
and
Shu, Jinlong
2021.
On the Turán Number of Theta Graphs.
Graphs and Combinatorics,
Vol. 37,
Issue. 6,
p.
2155.
Conlon, David
and
Tyomkyn, Mykhaylo
2021.
Repeated Patterns in Proper Colorings.
SIAM Journal on Discrete Mathematics,
Vol. 35,
Issue. 3,
p.
2249.
Kang, Dong Yeap
Kim, Jaehoon
and
Liu, Hong
2021.
On the rational Turán exponents conjecture.
Journal of Combinatorial Theory, Series B,
Vol. 148,
Issue. ,
p.
149.
Jiang, Tao
Ma, Jie
and
Yepremyan, Liana
2022.
On Turán exponents of bipartite graphs.
Combinatorics, Probability and Computing,
Vol. 31,
Issue. 2,
p.
333.
Zhai, Mingqing
and
Lin, Huiqiu
2023.
A strengthening of the spectral chromatic critical edge theorem: Books and theta graphs.
Journal of Graph Theory,
Vol. 102,
Issue. 3,
p.
502.
Jiang, Tao
Longbrake, Sean
and
Ma, Jie
2023.
Bipartite-ness under smooth conditions.
Combinatorics, Probability and Computing,
p.
1.
Liu, Xiao-Chuan
and
Yang, Xu
2023.
On the Turán Number of Generalized Theta Graphs.
SIAM Journal on Discrete Mathematics,
Vol. 37,
Issue. 2,
p.
1237.
Balogh, József
English, Sean
Heath, Emily
and
Krueger, Robert A.
2023.
Lower bounds on the Erdős–Gyárfás problem via color energy graphs.
Journal of Graph Theory,
Vol. 103,
Issue. 2,
p.
378.
Sun, Wanting
Li, Shuchao
and
Wei, Wei
2023.
Extensions on spectral extrema of C5/C6-free graphs with given size.
Discrete Mathematics,
Vol. 346,
Issue. 12,
p.
113591.
Xu, Yi
and
Li, Xin
2024.
On the spectral Turán problem of theta graphs.
Linear Algebra and its Applications,
Vol. 698,
Issue. ,
p.
40.
Bukh, Boris
2024.
Extremal graphs without exponentially small bicliques.
Duke Mathematical Journal,
Vol. 173,
Issue. 11,
Li, Xihe
Broersma, Hajo
and
Wang, Ligong
2024.
Growth rates of the bipartite Erdős–Gyárfás function.
Journal of Graph Theory,
Vol. 107,
Issue. 3,
p.
597.
Zhang, Tao
Xu, Zixiang
and
Ge, Gennian
2025.
A polynomial resultant approach to algebraic constructions of extremal graphs.
Science China Mathematics,
Vol. 68,
Issue. 2,
p.
485.
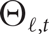 ${\Theta _{\ell ,t}}$
consists of two vertices joined by t vertex-disjoint paths, each of length
${\Theta _{\ell ,t}}$
consists of two vertices joined by t vertex-disjoint paths, each of length 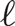 $\ell $
. For fixed odd
$\ell $
. For fixed odd 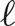 $\ell $
and large t, we show that the largest graph not containing
$\ell $
and large t, we show that the largest graph not containing 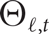 ${\Theta _{\ell ,t}}$
has at most
${\Theta _{\ell ,t}}$
has at most 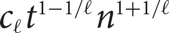 ${c_\ell }{t^{1 - 1/\ell }}{n^{1 + 1/\ell }}$
edges and that this is tight apart from the value of
${c_\ell }{t^{1 - 1/\ell }}{n^{1 + 1/\ell }}$
edges and that this is tight apart from the value of 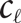 ${c_\ell }$
.
${c_\ell }$
.


