Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T13:56:51.874Z Has data issue: false hasContentIssue false
  • English
  • Français

Surprise Probabilities in Markov Chains

Part of: Markov processes

Published online by Cambridge University Press:  16 March 2017

JAMES NORRIS ,
YUVAL PERES  and
ALEX ZHAI
JAMES NORRIS
Affiliation:
Centre for Mathematical Sciences, University of Cambridge, Wilberforce Road, Cambridge CB3 0WB, UK (e-mail: [email protected])
YUVAL PERES
Affiliation:
Microsoft Research, Redmond, Washington, WA 98052, USA (e-mail: [email protected])
ALEX ZHAI
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA 94305, USA (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In a Markov chain started at a state x, the hitting time τ(y) is the first time that the chain reaches another state y. We study the probability 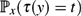$\mathbb{P}_x(\tau(y) = t)$ that the first visit to y occurs precisely at a given time t. Informally speaking, the event that a new state is visited at a large time t may be considered a ‘surprise’. We prove the following three bounds.

  • • In any Markov chain with n states, 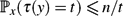$\mathbb{P}_x(\tau(y) = t) \le {n}/{t}$.

  • • In a reversible chain with n states, 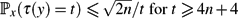$\mathbb{P}_x(\tau(y) = t) \le {\sqrt{2n}}/{t}$ for $t \ge 4n + 4$.

  • • For random walk on a simple graph with n ≥ 2 vertices, 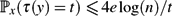$\mathbb{P}_x(\tau(y) = t) \le 4e \log(n)/t$.

We construct examples showing that these bounds are close to optimal. The main feature of our bounds is that they require very little knowledge of the structure of the Markov chain.

To prove the bound for random walk on graphs, we establish the following estimate conjectured by Aldous, Ding and Oveis-Gharan (private communication): for random walk on an n-vertex graph, for every initial vertex x,

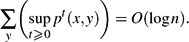$$ \sum_y \biggl( \sup_{t \ge 0} p^t(x, y) \biggr) = O(\log n). $$

MSC classification

Primary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 26 , Issue 4 , July 2017 , pp. 603 - 627
Copyright
Copyright © Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Basu, R., Hermon, J. and Peres, Y. (2015) Characterization of cutoff for reversible Markov chains. Ann. Probab., to appear. An extended abstract appeared in Proc. Twenty-Sixth Annual ACM–SIAM Symposium on Discrete Algorithms, SIAM.CrossRefGoogle Scholar
[2] Durrett, R. (2010) Probability: Theory and Examples, Cambridge University Press.CrossRefGoogle Scholar
[3] Feller, W. (1957) An Introduction to Probability Theory and its Applications, Vol. I, Wiley.Google Scholar
[4] Gurel-Gurevich, O. and Nachmias, A. (2013) Nonconcentration of return times. Ann. Probab. 41 848–870.CrossRefGoogle Scholar
[5] Lawler, G. (1980) A self-avoiding random walk. Duke Math. J. 47 655–693.CrossRefGoogle Scholar
[6] Lawler, G. (1991) Intersections of Random Walks, Birkhäuser.Google Scholar
[7] Levin, D. A., Peres, Y. and Wilmer, E. L. (2009) Markov Chains and Mixing Times, AMS.Google Scholar
[8] Miclo, L. (2010) On absorption times and Dirichlet eigenvalues. ESAIM: Probab. Statist. 14 117–150.CrossRefGoogle Scholar
[9] Peres, Y. and Sousi, P. (2015) Total variation cutoff in a tree. Annales de la faculté des sciences de Toulouse 24 763–779.Google Scholar
[10] Starr, N. (1966) Operator limit theorems. Trans. Amer. Math. Soc. 121 90–115.CrossRefGoogle Scholar
[11] Wilson, D. B. (1996) Generating random spanning trees more quickly than the cover time. In Proc. Twenty-Eighth Annual ACM Symposium on Theory of Computing, ACM, pp. 296–303.CrossRefGoogle Scholar