No CrossRef data available.
Article contents
The string of diamonds is nearly tight for rumour spreading
Published online by Cambridge University Press: 04 November 2019
Abstarct
For a rumour spreading protocol, the spread time is defined as the first time everyone learns the rumour. We compare the synchronous push&pull rumour spreading protocol with its asynchronous variant, and show that for any n-vertex graph and any starting vertex, the ratio between their expected spread times is bounded by 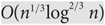 $O({n^{1/3}}{\log ^{2/3}}n)$. This improves the
$O({n^{1/3}}{\log ^{2/3}}n)$. This improves the 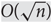 $O(\sqrt n)$ upper bound of Giakkoupis, Nazari and Woelfel (2016). Our bound is tight up to a factor of O(log n), as illustrated by the string of diamonds graph. We also show that if, for a pair α, β of real numbers, there exist infinitely many graphs for which the two spread times are nα and nβ in expectation, then
$O(\sqrt n)$ upper bound of Giakkoupis, Nazari and Woelfel (2016). Our bound is tight up to a factor of O(log n), as illustrated by the string of diamonds graph. We also show that if, for a pair α, β of real numbers, there exist infinitely many graphs for which the two spread times are nα and nβ in expectation, then 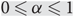 $0 \le \alpha \le 1$ and
$0 \le \alpha \le 1$ and  $\alpha \le \beta \le {1 \over 3} + {2 \over 3} \alpha $; and we show each such pair α, β is achievable.
$\alpha \le \beta \le {1 \over 3} + {2 \over 3} \alpha $; and we show each such pair α, β is achievable.
- Type
- Paper
- Information
- Copyright
- © Cambridge University Press 2019
Footnotes
A preliminary version of this paper appeared in Proceedings of the 21st International Workshop on Randomization and Computation (RANDOM’2017). This full version includes a new result, namely Theorem 2.5.
Supported by NSERC.
Supported by an NSERC Postdoctoral Fellowship and a Simons–Berkeley Research Fellowship. Part of this work was done while this author was at the Simons Institute for the Theory of Computing at UC Berkeley. Currently at McGill University.


