Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T13:30:52.968Z Has data issue: false hasContentIssue false
  • English
  • Français

A Stability Result for the Union-Closed Size Problem

Part of: Extremal combinatorics Combinatorics

Published online by Cambridge University Press:  18 August 2015

TOM ECCLES
TOM ECCLES*
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, Wilberforce Road, Cambridge CB3 0WB, UK (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

A family of sets is called union-closed if whenever A and B are sets of the family, so is A ∪ B. The long-standing union-closed conjecture states that if a family of subsets of [n] is union-closed, some element appears in at least half the sets of the family. A natural weakening is that the union-closed conjecture holds for large families, that is, families consisting of at least p02n sets for some constant p0. The first result in this direction appears in a recent paper of Balla, Bollobás and Eccles [1], who showed that union-closed families of at least 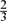$\tfrac{2}{3}$2n sets satisfy the conjecture; they proved this by determining the minimum possible average size of a set in a union-closed family of given size. However, the methods used in that paper cannot prove a better constant than 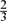$\tfrac{2}{3}$. Here, we provide a stability result for the main theorem of [1], and as a consequence we prove the union-closed conjecture for families of at least (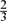$\tfrac{2}{3}$ − c)2n sets, for a positive constant c.

MSC classification

Primary: 05A18: Partitions of sets
Secondary: 05D05: Extremal set theory
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 25 , Issue 3 , May 2016 , pp. 399 - 418
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Balla, I., Bollobás, B. and Eccles, T. (2013) On union-closed families of sets. J. Combin. Theory Ser. A 120 531–544.Google Scholar
[2] Bollobás, B. and Leader, I. (1991) Compressions and isoperimetric inequalities. J. Combin. Theory Ser. A 56 47–62.Google Scholar
[3] Czédli, G., Maróti, M. and Schmidt, E. T. (2009) On the scope of averaging for Frankl's conjecture. Order 26 31–48.Google Scholar
[4] Duffus, D. (1985) In Graphs and Order (Rival, I., ed.), Reidel, p. 525.Google Scholar
[5] Harris, T. E. (1960) A lower bound for the critical probability in a certain percolation process. Math. Proc. Cambridge Philos. Soc. 26 13–20.CrossRefGoogle Scholar
[6] Katona, G. O. H. (1968) A theorem on finite sets. In Theory of Graphs (Erdős, P. and Katona, G. O. H., eds), Akadémiai Kiadó, pp. 187–207.Google Scholar
[7] Kruskal, J. B. (1963) The number of simplices in a complex. In Mathematical Optimization Techniques, University of California Press, pp. 251–278.Google Scholar
[8] Reimer, D. (2003) An average set size theorem. Combin. Probab. Comput. 12 89–93.CrossRefGoogle Scholar