Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-11T05:10:10.305Z Has data issue: false hasContentIssue false
  • English
  • Français

A smoother notion of spread hypergraphs

Part of: Graph theory

Published online by Cambridge University Press:  08 June 2023

Sam Spiro
Sam Spiro*
Affiliation:
Department of Mathematics, University of California San Diego, La Jolla, CA, USA
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Alweiss, Lovett, Wu, and Zhang introduced 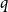$q$-spread hypergraphs in their breakthrough work regarding the sunflower conjecture, and since then 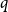$q$-spread hypergraphs have been used to give short proofs of several outstanding problems in probabilistic combinatorics. A variant of 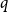$q$-spread hypergraphs was implicitly used by Kahn, Narayanan, and Park to determine the threshold for when a square of a Hamiltonian cycle appears in the random graph 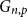$G_{n,p}$. In this paper, we give a common generalization of the original notion of 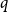$q$-spread hypergraphs and the variant used by Kahn, Narayanan, and Park.

Keywords

thresholdshypergraphsspread

MSC classification

Primary: 05C80: Random graphs
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 32 , Issue 5 , September 2023 , pp. 809 - 818
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This material is based upon work supported by the National Science Foundation Graduate Research Fellowship under Grant No. DGE-1650112.

References

Alon, N. and Spencer, J. H. (2004) The Probabilistic Method. John Wiley & Sons.Google Scholar
Alweiss, R., Lovett, S., Wu, K. and Zhang, J. (2020) Improved bounds for the sunflower lemma. In Proceedings of the 52nd Annual ACM SIGACT Symposium on Theory of Computing, pp. 624–630.10.1145/3357713.3384234CrossRefGoogle Scholar
Espuny Díaz, A. and Person, Y. (2021) Spanning $F$ -cyles in random graphs. arXiv preprint arXiv: 2106.10023.Google Scholar
Frankston, K., Kahn, J., Narayanan, B. and Park, J. (2021) Thresholds versus fractional expectation-thresholds. Ann. Math. 194(2) 475–495.CrossRefGoogle Scholar
Frieze, A. and Marbach, T. G. (2021) Rainbow thresholds. arXiv preprint arXiv: 2104.05629.Google Scholar
Johansson, A., Kahn, J. and Vu, V. (2008) Factors in random graphs. Random Struct. Algorithms 33(1) 1–28.10.1002/rsa.20224CrossRefGoogle Scholar
Kahn, J., Narayanan, B. and Park, J. (2021) The threshold for the square of a hamilton cycle. Proc. Am. Math. Soc. 149(8) 3201–3208.CrossRefGoogle Scholar