Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-25T17:03:14.499Z Has data issue: false hasContentIssue false
  • English
  • Français

The Size of a Hypergraph and its Matching Number

Published online by Cambridge University Press:  20 January 2012

HAO HUANG ,
PO-SHEN LOH  and
BENNY SUDAKOV
HAO HUANG
Affiliation:
Department of Mathematics, UCLA, Los Angeles, CA 90095, USA (e-mail: [email protected], [email protected])
PO-SHEN LOH
Affiliation:
Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, PA 15213, USA (e-mail: [email protected])
BENNY SUDAKOV
Affiliation:
Department of Mathematics, UCLA, Los Angeles, CA 90095, USA (e-mail: [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

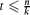More than forty years ago, Erdős conjectured that for any , every k-uniform hypergraph on n vertices without t disjoint edges has at most max 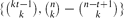edges. Although this appears to be a basic instance of the hypergraph Turán problem (with a t-edge matching as the excluded hypergraph), progress on this question has remained elusive. In this paper, we verify this conjecture for all 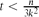. This improves upon the best previously known range 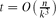, which dates back to the 1970s.

Keywords

Primary 05D1505C65
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 21 , Issue 3 , May 2012 , pp. 442 - 450
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Aharoni, R. and Howard, D. Size conditions for the existence of rainbow matchings. Submitted.Google Scholar
[2]Alon, N., Frankl, P., Huang, H., Rödl, V., Ruciński, A. and Sudakov, B. Large matchings in uniform hypergraphs and the conjectures of Erdős and Samuels. Submitted.Google Scholar
[3]Alon, N., Huang, H. and Sudakov, B. Nonnegative k-sums, fractional covers, and probability of small deviations. Submitted.Google Scholar
[4]Bollobás, B., Daykin, D. E. and Erdős, P. (1976) Sets of independent edges of a hypergraph. Quart. J. Math. Oxford Ser. 2, 27 25–32.Google Scholar
[5]Erdős, P. (1965) A problem on independent r-tuples. Ann. Univ. Sci. Budapest. Eötvös Sect. Math. 8 93–95.Google Scholar
[6]Erdős, P. and Gallai, T. (1959) On the maximal paths and circuits of graphs. Acta Math. Acad. Sci. Hungar. 10 337–357.CrossRefGoogle Scholar
[7]Erdős, P., Ko, C. and Rado, R. (1961) Intersection theorems for systems of finite sets. Quart. J. Math. Oxford Ser. 2 12 313–318.CrossRefGoogle Scholar
[8]Frankl, P. (1987) The shifting techniques in extremal set theory. In Surveys in Combinatorics, Vol. 123 of London Mathematical Society Lecture Notes, Cambridge University Press, pp. 81–110.Google Scholar
[9]Frankl, P., Rödl, V. and Ruciński, A. On the maximum number of edges in a triple system not containing a disjoint family of a given size, to appear.Google Scholar
[10]Kleitman, D. (1968) On a conjecture of Milner on k-graphs with non-disjoint edges. J. Combin. Theory 5 153–156.Google Scholar
[11]Pyber, L. (1986) A new generalization of the Erdős–Ko–Rado theorem. J. Combin. Theory Ser. A 43 85–90.Google Scholar
[12]Samuels, S. M. (1966) On a Chebyshev-type inequality for sums of independent random variables. Ann. Math. Statist. 37 248–259.CrossRefGoogle Scholar