Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T14:15:30.811Z Has data issue: false hasContentIssue false
  • English
  • Français

A Separator Theorem for String Graphs and its Applications

Published online by Cambridge University Press:  07 October 2009

JACOB FOX  and
JÁNOS PACH
JACOB FOX
Affiliation:
Department of Mathematics, Princeton, NJ 08544, USA (e-mail: [email protected])
JÁNOS PACH
Affiliation:
EPFL Lausanne, IMB-DCG, Station 8, CH-1015, Switzerland and Rényi Institute, Budapest, H-1364, Hungary (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

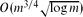A string graph is the intersection graph of a collection of continuous arcs in the plane. We show that any string graph with m edges can be separated into two parts of roughly equal size by the removal of vertices. This result is then used to deduce that every string graph with n vertices and no complete bipartite subgraph Kt,t has at most ctn edges, where ct is a constant depending only on t. Another application shows that locally tree-like string graphs are globally tree-like: for any ε > 0, there is an integer g(ε) such that every string graph with n vertices and girth at least g(ε) has at most (1 + ε)n edges. Furthermore, the number of such labelled graphs is at most (1 + ε)nT(n), where T(n) = nn−2 is the number of labelled trees on n vertices.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 19 , Issue 3 , May 2010 , pp. 371 - 390
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Alon, N., Seymour, P. and Thomas, R. (1990) A separator theorem for nonplanar graphs. J. Amer. Math. Soc. 3 801–808.CrossRefGoogle Scholar
[2]Alon, N. and Spencer, J. (2000) The Probabilistic Method, 2nd edn, Wiley.CrossRefGoogle Scholar
[3]Bollobás, B. (1998) Modern Graph Theory, Springer.CrossRefGoogle Scholar
[4]Böttcher, J., Pruessmann, K. P., Taraz, A. and Würfl, A. (2008) Bandwidth, treewidth, separators, expansion, and universality. In Proc. Topological. and Geometric Graph Theory (TGGT 08), Electron. Notes. Discrete Math. 31 91–96.CrossRefGoogle Scholar
[5]Capoyleas, V. and Pach, J. (1992) A Turán-type theorem on chords of a convex polygon. J. Combin. Theory Ser. B 56 9–15.Google Scholar
[6]Chung, F. (1988) Labelings of graphs. In Selected Topics in Graph Theory, Academic Press, San Diego, pp. 151–168.Google Scholar
[7]Diestel, R. (2000) Graph Theory, 2nd edn, Springer.Google Scholar
[8]Dvořák, Z. and Norine, S. Small graph classes and bounded expansion. J. Combin. Theory Ser. B, to appear.Google Scholar
[9]Erdős, P. (1959) Graph theory and probability. Canad. J. Math. 11 34–38.CrossRefGoogle Scholar
[10]Fox, J. (2006) A bipartite analogue of Dilworth's theorem. Order 23 197–209.Google Scholar
[11]Fox, J. and Pach, J. (2008) Separator theorems and Turán-type results for planar intersection graphs. Adv. Math. 219 1070–1080.CrossRefGoogle Scholar
[12]Fox, J. and Pach, J. (2008) Coloring Kk-free intersection graphs of geometric objects in the plane. In Proc. 24th ACM Sympos. on Computational Geometry, ACM Press, New York, pp. 346–354.Google Scholar
[13]Fox, J. and Pach, J. String graphs and incomparability graphs. Submitted.Google Scholar
[14]Fox, J., Pach, J. and Tóth, C. D. Intersection patterns of curves. J. London Math. Soc., to appear.Google Scholar
[15]Fox, J., Pach, J. and Tóth, C. D. Turán-type results for partial orders and intersection graphs of convex sets. Israel J. Math, to appear.Google Scholar
[16]Gilbert, J. R., Hutchinson, J. P. and Tarjan, R. E. (1984) A separator theorem for graphs of bounded genus. J. Algorithms 5 391–407.CrossRefGoogle Scholar
[17]Koebe, P. (1936) Kontaktprobleme der konformen Abbildung. Berichte über die Verhandlungen der Sachsischen Akademie der Wissenschaften, Leipzig, Mathematische-Physische Klasse 88 141–164.Google Scholar
[18]Kolman, P. and Matoušek, J. (2004) Crossing number, pair-crossing number, and expansion. J. Combin. Theory Ser. B 92 99–113.CrossRefGoogle Scholar
[19]Kostochka, A. V. and Nešetřil, J. (1998) Coloring relatives of intervals on the plane I: Chromatic number versus girth. Europ. J. Combin. 19 103–110.CrossRefGoogle Scholar
[20]Knopp, K. (1956) Infinite Sequences and Series, Dover, New York.Google Scholar
[21]Kratochvíl, J. and Matoušek, J. (1989) NP-hardness results for intersection graphs. Comment. Math. Univ. Carolin. 30 761–773.Google Scholar
[22]Kratochvíl, J. and Matoušek, J. (1994) Intersection graphs of segments. J. Combin. Theory Ser. B 62 289–315.CrossRefGoogle Scholar
[23]Kühn, D. and Osthus, D. (2004) Induced subdivisions in Ks,s-free graphs of large average degree. Combinatorica 24 287–304.CrossRefGoogle Scholar
[24]Leighton, T. and Rao, S. (1999) Multicommodity max-flow min-cut theorems and their use in designing approximation algorithms. J. Assoc. Comput. Mach. 46 787–832.CrossRefGoogle Scholar
[25]Lipton, R. J., Rose, D. J. and Tarjan, R. E. (1979) Generalized nested dissection. SIAM J. Numer. Anal. 16 346–358.CrossRefGoogle Scholar
[26]Lipton, R. J. and Tarjan, R. E. (1979) A separator theorem for planar graphs. SIAM J. Appl. Math. 36 177–189.CrossRefGoogle Scholar
[27]Lipton, R. J. and Tarjan, R. E. (1980) Applications of a planar separator theorem. SIAM J. Comput. 9 615–627.Google Scholar
[28]McDiarmid, C., Steger, A. and Welsh, D. (2005) Random planar graphs. J. Combin. Theory Ser. B 93 187–206.Google Scholar
[29]Miller, G. L., Teng, S.-H., Thurston, W. and Vavasis, S. A. (1997) Separators for sphere-packings and nearest neighbor graphs. J. Assoc. Comput. Mach. 44 1–29.CrossRefGoogle Scholar
[30]Norine, S., Seymour, P., Thomas, R. and Wollan, P. (2006) Proper minor-closed families are small. J. Combin. Theory Ser. B 96 754–757.Google Scholar
[31]Pach, J. and Agarwal, P. (1995) Combinatorial Geometry, Wiley, New York.CrossRefGoogle Scholar
[32]Pach, J., Pinchasi, R., Sharir, M. and Tóth, G. (2005) Topological graphs with no large grids. Graphs Combin. 21 355–364.CrossRefGoogle Scholar
[33]Pach, J., Shahrokhi, F. and Szegedy, M. (1996) Applications of the crossing number. Algorithmica 16 111–117.Google Scholar
[34]Pach, J. and Sharir, M. (2009) On planar intersection graphs with forbidden subgraphs. J. Graph Theory 59 205–214.CrossRefGoogle Scholar
[35]Pach, J. and Tóth, G. (2000) Which crossing number is it anyway? J. Combin. Theory Ser. B 80 225–246.Google Scholar
[36]Pach, J. and Tóth, G. (2006) Comment on Fox News. Geombinatorics 15 150–154.Google Scholar
[37]Preparata, F. and Shamos, M. (1985) Computational geometry: An Introduction, Texts and Monographs in Computer Science, Springer, New York.CrossRefGoogle Scholar
[38]Radoičić, R. and Tóth, G. (2008) The discharging method in combinatorial geometry and its application to Pach–Sharir conjecture on intersection graphs. In Proc. Joint Summer Research Conference on Discrete and Computational Geometry (Goodman, J. E., Pach, J. and Pollack, J., eds), Vol. 453 of Contemporary Mathematics, AMS, pp. 319–342.Google Scholar
[39]Thomassen, C. (1983) Girth in graphs. J. Combin. Theory Ser. B 35 129–141.CrossRefGoogle Scholar