Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T13:42:20.330Z Has data issue: false hasContentIssue false
  • English
  • Français

Robust Tverberg and Colourful Carathéodory Results via Random Choice

Part of: General convexity Extremal combinatorics

Published online by Cambridge University Press:  19 December 2017

PABLO SOBERÓN
PABLO SOBERÓN*
Affiliation:
Mathematics Department, Northeastern University, Boston, MA 02445, USA (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We use the probabilistic method to obtain versions of the colourful Carathéodory theorem and Tverberg's theorem with tolerance.

In particular, we give bounds for the smallest integer N = N(t,d,r) such that for any N points in ℝd, there is a partition of them into r parts for which the following condition holds: after removing any t points from the set, the convex hulls of what is left in each part intersect.

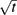We prove a bound N = rt + O($\sqrt{t}$) for fixed r,d which is polynomial in each parameters. Our bounds extend to colourful versions of Tverberg's theorem, as well as Reay-type variations of this theorem.

MSC classification

Primary: 52A35: Helly-type theorems and geometric transversal theory
Secondary: 05D40: Probabilistic methods
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 27 , Issue 3 , May 2018 , pp. 427 - 440
Copyright
Copyright © Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Ajtai, M., Chvátal, V., Newborn, M. M. and Szemerédi, E. (1982) Crossing-free subgraphs. In Theory and Practice of Combinatorics, Vol. 60 of North-Holland Mathematics Studies, North-Holland, pp. 9–12.Google Scholar
[2] Alon, N. and Spencer, J. H. (2008) The Probabilistic Method, third edition, Wiley-Interscience Series in Discrete Mathematics and Optimization, Wiley.Google Scholar
[3] Arocha, J. L., Bárány, I., Bracho, J., Fabila, R. and Montejano, L. (2009) Very colorful theorems. Discrete Comput. Geom. 42 142–154.Google Scholar
[4] Asada, M., Chen, R., Frick, F., Huang, F., Polevy, M., Stoner, D., Tsang, L. H. and Wellner, Z. (2016) On Reay's relaxed Tverberg conjecture and generalizations of Conway's thrackle conjecture. arXiv:1608.04279Google Scholar
[5] Bárány, I. (1982) A generalization of Carathéodory's theorem. Discrete Math. 40 141–152.CrossRefGoogle Scholar
[6] Bárány, I. (2015) Tensors, colours, octahedra. In Geometry, Structure and Randomness in Combinatorics (Matoušek, J. et al., eds), Edizione della Normale, pp. 1–17.Google Scholar
[7] Bárány, I. Personal communication.Google Scholar
[8] Bárány, I. and Larman, D. G. (1992) A colored version of Tverberg's theorem. J. London Math. Soc. s2-45 314–320.Google Scholar
[9] Bárány, I. and Onn, S. (1997) Colourful linear programming and its relatives. Math. Oper. Res. 22 550–567.Google Scholar
[10] Blagojević, P. V. M., Frick, F. and Ziegler, G. M. (2014) Tverberg plus constraints. Bull. London Math. Soc. 46 953–967.Google Scholar
[11] Blagojević, P. V. M., Matschke, B. and Ziegler, G. M. (2011) Optimal bounds for a colorful Tverberg–Vrećica type problem. Adv. Math. 226 5198–5215.Google Scholar
[12] Blagojević, P. V. M., Matschke, B. and Ziegler, G. M. (2015) Optimal bounds for the colored Tverberg problem. J. Eur. Math. Soc. 17 739–754.Google Scholar
[13] Chazelle, B. and Friedman, J. (1990) A deterministic view of random sampling and its use in geometry. Combinatorica 10 229–249.CrossRefGoogle Scholar
[14] Clarkson, K. L. (1987) New applications of random sampling in computational geometry. Discrete Comput. Geom. 2 195–222.Google Scholar
[15] Clarkson, K. L., Eppstein, D., Miller, G. L., Sturtivant, C. and Teng, S.-H. (1996) Approximating center points with iterative Radon points. Internat. J. Comput. Geom. Appl. 6 357–377.Google Scholar
[16] Forge, D., Las Vergnas, M. and Schuchert, P. (2001) 10 points in dimension 4 not projectively equivalent to the vertices of a convex polytope. Europ. J. Combin. 22 705–708.CrossRefGoogle Scholar
[17] García-Colín, N. (2007) Applying Tverberg type theorems to geometric problems. PhD thesis, University College London.Google Scholar
[18] García-Colín, N. and Larman, D. (2015) Projective equivalences of k-neighbourly polytopes. Graphs Combin. 31 1403–1422.Google Scholar
[19] García-Colín, N., Raggi, M. and Roldán-Pensado, E. (2017) A note on the tolerant Tverberg theorem. Discrete Comput. Geom. 58, no. 3, 746–754.Google Scholar
[20] Haussler, D. and Welzl, E. (1987) ϵ-nets and simplex range queries. Discrete Comput. Geom. 2 127–151.Google Scholar
[21] Holmsen, A. F. (2016) The intersection of a matroid and an oriented matroid. Adv. Math. 290 1–14.Google Scholar
[22] Holmsen, A. F., Pach, J. and Tverberg, H. (2008) Points surrounding the origin. Combinatorica 28 633–644.CrossRefGoogle Scholar
[23] Larman, D. G. (1972) On sets projectively equivalent to the vertices of a convex polytope. Bull. London Math. Soc. 4 6–12.Google Scholar
[24] Liu, R. Y., Serfling, R. J. and Souvaine, D. L. (2006) Data Depth: Robust Multivariate Analysis, Computational Geometry, and Applications, Vol. 72 of DIMAC Series in Discrete Mathematics and Theoretical Computer Science, AMS.Google Scholar
[25] Matoušek, J. (2002) Lectures on Discrete Geometry, Vol. 212 of Graduate Texts in Mathematics, Springer.Google Scholar
[26] Miller, G. L. and Sheehy, D. R. (2009) Approximate center points with proofs. In SCG '09: Twenty-Fifth Annual Symposium on Computational Geometry, ACM, pp. 153–158.Google Scholar
[27] Montejano, L. and Oliveros, D. (2011) Tolerance in Helly-type theorems. Discrete Comput. Geom. 45 348–357.Google Scholar
[28] Mulzer, W. and Stein, Y. (2013) Algorithms for tolerated Tverberg partitions. In ISAAC 2013: International Symposium on Algorithms and Computation, Springer, pp. 295–305.Google Scholar
[29] Perles, M. A. and Sigron, M. (2016) Some variations on Tverberg's theorem. Israel J. Math. 216 957–972.Google Scholar
[30] Reay, J. R. (1979) Several generalizations of Tverberg's theorem. Israel J. Math. 34 238–244.Google Scholar
[31] Rolnick, D. and Soberón, P. (2016) Algorithms for Tverberg's theorem via centerpoint theorems. arXiv:1601.03083v2Google Scholar
[32] Sarkaria, K. S. (1992) Tverberg's theorem via number fields. Israel J. Math. 79 317–320.Google Scholar
[33] Soberón, P. (2015) Equal coefficients and tolerance in coloured Tverberg partitions. Combinatorica 35 235–252.Google Scholar
[34] Soberón, P. and Strausz, R. (2012) A generalisation of Tverberg's theorem. Discrete Comput. Geom. 47 455–460.CrossRefGoogle Scholar
[35] Székely, L. A. (1997) Crossing numbers and hard Erdős problems in discrete geometry. Combin. Probab. Comput. 6 353–358.Google Scholar
[36] Tukey, J. W. (1975) Mathematics and the picturing of data. In Proceedings of the International Congress of Mathematicians, Vol. 2, Canadian Mathematical Congress, pp. 523–531.Google Scholar
[37] Tverberg, H. (1966) A generalization of Radon's theorem. J. London Math. Soc. 41 123–128.Google Scholar