Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-24T13:21:18.197Z Has data issue: false hasContentIssue false
  • English
  • Français

Resolution of T. Ward's Question and the Israel–Finch Conjecture: Precise Analysis of an Integer Sequence Arising in Dynamics

Published online by Cambridge University Press:  02 October 2014

JEFFREY GAITHER ,
GUY LOUCHARD ,
STEPHAN WAGNER  and
MARK DANIEL WARD
JEFFREY GAITHER
Affiliation:
Department of Mathematics, Purdue University, 150 North University Street, West Lafayette, IN 47907–2067, USA (e-mail: [email protected])
GUY LOUCHARD
Affiliation:
Département d'Informatique, Université Libre de Bruxelles, CP 212, Boulevard du Triomphe, B-1050, Bruxelles, Belgium (e-mail: [email protected])
STEPHAN WAGNER
Affiliation:
Department of Mathematical Sciences, Stellenbosch University, Private Bag X1, Matieland 7602, South Africa (e-mail: [email protected])
MARK DANIEL WARD
Affiliation:
Department of Statistics, Purdue University, 150 North University Street, West Lafayette, IN 47907–2067, USA (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyse the first-order asymptotic growth of

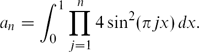\[ a_{n}=\int_{0}^{1}\prod_{j=1}^{n}4\sin^{2}(\pi jx)\, dx. \]
The integer an appears as the main term in a weighted average of the number of orbits in a particular quasihyperbolic automorphism of a 2n-torus, which has applications to ergodic and analytic number theory. The combinatorial structure of an is also of interest, as the ‘signed’ number of ways in which 0 can be represented as the sum of ϵjj for −n ≤ j ≤ n (with j ≠ 0), with ϵj ∈ {0, 1}. Our result answers a question of Thomas Ward (no relation to the fourth author) and confirms a conjecture of Robert Israel and Steven Finch.

Keywords

Primary 05A16Secondary 41A6005A17
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 24 , Special Issue 1: Honouring the Memory of Philippe Flajolet - Part 3 , January 2015 , pp. 195 - 215
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bleistein, N. and Handelsman, R. (2010) Asymptotic Expansions of Integrals, Dover.Google Scholar
[2] Clark, L. (2000) On the representation of m as $\sum_{k=-n}^n \varepsilon_k k$ . Internat. J. Math. Math. Sci. 23 77–80.Google Scholar
[3] Entringer, R. C. (1968) Representation of m as $\sum_{k=-n}^n \varepsilon_k k$ . Canad. Math. Bull. 11 289–293.Google Scholar
[4] Finch, S. R. (2009) Signum equations and extremal coefficients. http://www.people.fas.harvard.edu/~sfinch/csolve/signm.pdf.Google Scholar
[5] Flajolet, P. and Sedgewick, R. (2009) Analytic Combinatorics, Cambridge University Press.Google Scholar
[6] Israel, R. (2008) Post on the newsgroup sci.math.research, 17 January 2008.Google Scholar
[7] Jaidee, S., Stevens, S. and Ward, T. (2011) Mertens' theorem for toral automorphisms. Proc. Amer. Math. Soc. 139 1819–1824.CrossRefGoogle Scholar
[8] Lieb, E. H. and Loss, M. (2001) Analysis, second edition, Vol. 14 of Graduate Studies in Mathematics, AMS.Google Scholar
[9] Louchard, G. and Prodinger, H. (2009) Representations of numbers as $\sum_{k=-n}^n \varepsilon_k k$ : A saddle point approach. In Infinity in Logic and Computation (Archibald, M., Brattka, V., Goranko, V. and Löwe, B., eds), Vol. 5489 of Lecture Notes in Computer Science, Springer, pp. 87–96.Google Scholar
[10] Morrison, K. E. (1995) Cosine products, Fourier transforms, and random sums. Amer. Math. Monthly 102 716–724.Google Scholar
[11] Noorani, M. and Salmi, M. (1999) Mertens theorem and closed orbits of ergodic toral automorphisms. Bull. Malaysian Math. Soc. (Second Series) 22 127–133.Google Scholar
[12] On-Line Encyclopedia of Integer Sequences . Sequence #A133871: http://oeis.org/A133871.Google Scholar
[13] Prodinger, H. (1979) On a generalization of the Dyck-language over a two letter alphabet. Discrete Math. 28 269–276.Google Scholar
[14] Prodinger, H. (1982) On the number of partitions of {1, . . ., N} into two sets of equal cardinalities and equal sums. Canad. Math. Bull. 25 238–241.CrossRefGoogle Scholar
[15] Prodinger, H. (1984) On the number of partitions of {1, . . ., n} into r sets of equal cardinalities and sums. Tamkang J. Math. 15 161–164.Google Scholar
[16] Schmidt, W. (1980) Diophantine Approximation, Vol. 785 of Lecture Notes in Mathematics, Springer.Google Scholar
[17] Stevens, S. (2012) Personal communication with the authors. Google Scholar
[18] van Lint, J. H. (1967) Representation of 0 as $\sum_{k=-N}^n \varepsilon_k k$ . Proc. Amer. Math. Soc. 18 182–184.Google Scholar
[19] Walters, P. (1969) Topological conjugacy of affine transformations of compact abelian groups. Trans. Amer. Math. Soc. 140 95–107.Google Scholar
[20] Ward, T. (2012) Personal communication with the authors.Google Scholar