Article contents
Resilience of the rank of random matrices
Published online by Cambridge University Press: 28 August 2020
Abstract
Let M be an n × m matrix of independent Rademacher (±1) random variables. It is well known that if 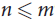 $n \leq m$, then M is of full rank with high probability. We show that this property is resilient to adversarial changes to M. More precisely, if
$n \leq m$, then M is of full rank with high probability. We show that this property is resilient to adversarial changes to M. More precisely, if 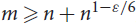 $m \ge n + {n^{1 - \varepsilon /6}}$, then even after changing the sign of (1 – ε)m/2 entries, M is still of full rank with high probability. Note that this is asymptotically best possible as one can easily make any two rows proportional with at most m/2 changes. Moreover, this theorem gives an asymptotic solution to a slightly weakened version of a conjecture made by Van Vu in [17].
$m \ge n + {n^{1 - \varepsilon /6}}$, then even after changing the sign of (1 – ε)m/2 entries, M is still of full rank with high probability. Note that this is asymptotically best possible as one can easily make any two rows proportional with at most m/2 changes. Moreover, this theorem gives an asymptotic solution to a slightly weakened version of a conjecture made by Van Vu in [17].
MSC classification
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 1
- Cited by



