No CrossRef data available.
Published online by Cambridge University Press: 21 October 2014
In this paper we study the following problem.
Discrete partitioning problem (DPP). Let 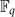 $\mathbb{F}_q$Pn denote the n-dimensional finite projective space over
$\mathbb{F}_q$Pn denote the n-dimensional finite projective space over 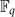 $\mathbb{F}_q$. For positive integer k ⩽ n, let {Ai}i = 1N be a partition of (
$\mathbb{F}_q$. For positive integer k ⩽ n, let {Ai}i = 1N be a partition of (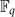 $\mathbb{F}_q$Pn)k such that:
$\mathbb{F}_q$Pn)k such that:
(1) for all i ⩽ N, Ai = ∏j=1kAji (partition into product sets),
(2) for all i ⩽ N, there is a (k − 1)-dimensional subspace Li ⊆ 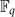 $\mathbb{F}_q$Pn such that Ai ⊆ (Li)k.
$\mathbb{F}_q$Pn such that Ai ⊆ (Li)k.
DPP arises in an approach that we propose for proving lower bounds for the query complexity of generating random points from convex bodies. It is also related to other partitioning problems in combinatorics and complexity theory. We conjecture an asymptotically optimal partition for DPP and show that it is optimal in two cases: when the dimension is low (k = n = 2) and when the factors of the parts are structured, namely factors of a part are close to being a subspace. These structured partitions arise naturally as partitions induced by query algorithms. Our problem does not seem to be directly amenable to previous techniques for partitioning lower bounds such as rank arguments, although rank arguments do lie at the core of our techniques.