Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
2000.
Random Graphs.
p.
307.
Burshtein, D.
Krivelevich, M.
Litsyn, S.
and
Miller, G.
2002.
Upper bounds on the rate of LDPC codes.
IEEE Transactions on Information Theory,
Vol. 48,
Issue. 9,
p.
2437.
Kim, Jeong Han
2003.
Perfect matchings in random uniform hypergraphs.
Random Structures & Algorithms,
Vol. 23,
Issue. 2,
p.
111.
Molloy, Michael
2005.
Cores in random hypergraphs and Boolean formulas.
Random Structures & Algorithms,
Vol. 27,
Issue. 1,
p.
124.
Feige, Uriel
Kim, Jeong
and
Ofek, Eran
2006.
Witnesses for non-satisfiability of dense random 3CNF formulas.
p.
497.
Plummer, Michael D.
2007.
Graph factors and factorization: 1985–2003: A survey.
Discrete Mathematics,
Vol. 307,
Issue. 7-8,
p.
791.
Janson, Svante
and
Wormald, Nicholas
2007.
Rainbow Hamilton cycles in random regular graphs.
Random Structures & Algorithms,
Vol. 30,
Issue. 1-2,
p.
35.
Johansson, Anders
Kahn, Jeff
and
Vu, Van
2008.
Factors in random graphs.
Random Structures & Algorithms,
Vol. 33,
Issue. 1,
p.
1.
Mennink, Bart
2012.
Increasing the flexibility of the herding attack.
Information Processing Letters,
Vol. 112,
Issue. 3,
p.
98.
Cooper, Colin
Frieze, Alan
and
Radzik, Tomasz
2013.
The cover times of random walks on random uniform hypergraphs.
Theoretical Computer Science,
Vol. 509,
Issue. ,
p.
51.
Dudek, Andrzej
Frieze, Alan
Ruciński, Andrzej
and
Šileikis, Matas
2013.
Approximate counting of regular hypergraphs.
Information Processing Letters,
Vol. 113,
Issue. 19-21,
p.
785.
Bodó, Ágnes
Katona, Gyula Y.
and
Simon, Péter L.
2016.
SIS Epidemic Propagation on Hypergraphs.
Bulletin of Mathematical Biology,
Vol. 78,
Issue. 4,
p.
713.
Blinovsky, Vladimir
and
Greenhill, Catherine
2016.
Asymptotic enumeration of sparse uniform hypergraphs with given degrees.
European Journal of Combinatorics,
Vol. 51,
Issue. ,
p.
287.
Sen, Subhabrata
2018.
Optimization on sparse random hypergraphs and spin glasses.
Random Structures & Algorithms,
Vol. 53,
Issue. 3,
p.
504.
Benevides, Fabrício S.
Gerbner, Dániel
Palmer, Cory T.
and
Vu, Dominik K.
2018.
Identifying defective sets using queries of small size.
Discrete Mathematics,
Vol. 341,
Issue. 1,
p.
143.
Avin, Chen
Lotker, Zvi
Nahum, Yinon
and
Peleg, David
2019.
Random preferential attachment hypergraph.
p.
398.
Aldosari, Haya S.
and
Greenhill, Catherine
2019.
Enumerating sparse uniform hypergraphs with given degree sequence and forbidden edges.
European Journal of Combinatorics,
Vol. 77,
Issue. ,
p.
68.
Antelmi, Alessia
Cordasco, Gennaro
Spagnuolo, Carmine
and
Szufel, Przemysław
2020.
Algorithms and Models for the Web Graph.
Vol. 12091,
Issue. ,
p.
36.
Altman, Daniel
Greenhill, Catherine
Isaev, Mikhail
and
Ramadurai, Reshma
2020.
A threshold result for loose Hamiltonicity in random regular uniform hypergraphs.
Journal of Combinatorial Theory, Series B,
Vol. 142,
Issue. ,
p.
307.
Immorlica, Nicole
Kanoria, Yash
and
Lu, Jiaqi
2020.
When does Competition and Costly Information Acquisition Lead to a Deadlock?.
SSRN Electronic Journal ,
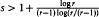 The Proof is based on the application of a technique of Robinson and Wormald [7, 8]. The space of hypergraphs is partitioned into subsets according to the number of small cycles in the hypergraph. The difference in the expected number of perfect matchings between these subsets explains most of the variance of the number of perfect matchings in the space of hypergraphs, and is sufficient to prove existence (whp), using the Chebychev Inequality.
The Proof is based on the application of a technique of Robinson and Wormald [7, 8]. The space of hypergraphs is partitioned into subsets according to the number of small cycles in the hypergraph. The difference in the expected number of perfect matchings between these subsets explains most of the variance of the number of perfect matchings in the space of hypergraphs, and is sufficient to prove existence (whp), using the Chebychev Inequality.