Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T14:23:47.242Z Has data issue: false hasContentIssue false
  • English
  • Français

Partial Shadows of Set Systems

Part of: Extremal combinatorics Combinatorics

Published online by Cambridge University Press:  20 January 2015

BÉLA BOLLOBÁS  and
TOM ECCLES
BÉLA BOLLOBÁS
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, Wilberforce Road, Cambridge CB3 0WB, UK (e-mail: [email protected]) Department of Mathematical Sciences, University of Memphis, Memphis TN 38152, USA (e-mail: [email protected])
TOM ECCLES
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, Wilberforce Road, Cambridge CB3 0WB, UK (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The shadow of a system of sets is all sets which can be obtained by taking a set in the original system, and removing a single element. The Kruskal-Katona theorem tells us the minimum possible size of the shadow of 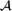$\mathcal A$, if 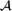$\mathcal A$ consists of m r-element sets.

In this paper, we ask questions and make conjectures about the minimum possible size of a partial shadow for 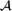$\mathcal A$, which contains most sets in the shadow of 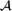$\mathcal A$. For example, if $\mathcal B$ is a family of sets containing all but one set in the shadow of each set of 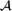$\mathcal A$, how large must $\mathcal B$ be?

MSC classification

Primary: 05D05: Extremal set theory
Secondary: 05A99: None of the above, but in this section
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 24 , Issue 5 , September 2015 , pp. 825 - 828
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Katona, G. O. H. (1968) A theorem of finite sets. In Theory of Graphs (Erdős, P. and Katona, G. O. H., eds), Conference in Tihany, Hungary, 1966, Academic Press and Akadémiai Kiadó, pp. 187–207.Google Scholar
[2] Kruskal, J. B. (1963) The number of simplices in a complex. In Mathematical Optimization Techniques, University of California Press, pp. 251–278.Google Scholar
[3] Lovász, L. (1979) Combinatorial Problems and Exercises, North-Holland.Google Scholar