No CrossRef data available.
Article contents
On the Ramsey numbers of daisies II
Published online by Cambridge University Press: 18 September 2024
Abstract
A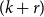 
$(k+r)$-uniform hypergraph 
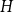$H$ on 
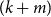$(k+m)$ vertices is an 
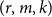$(r,m,k)$-daisy if there exists a partition of the vertices 
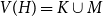$V(H)=K\cup M$ with 
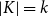$|K|=k$, 
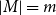$|M|=m$ such that the set of edges of 
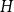$H$ is all the 
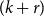$(k+r)$-tuples 
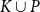$K\cup P$, where 
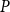$P$ is an 
$r$-tuple of 
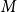$M$. We obtain an 
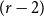$(r-2)$-iterated exponential lower bound to the Ramsey number of an 
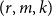$(r,m,k)$-daisy for 
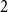$2$-colours. This matches the order of magnitude of the best lower bounds for the Ramsey number of a complete 
$r$-graph.
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
Footnotes
*
The author was supported by NSF grant DMS 1764385 and US Air Force grant FA9550-23-1-0298.
References
Bollobás, B., Leader, I. and Malvenuto, C. (2011) Daisies and other Turán problems. Combin. Probab. Comput. 20(5) 743–747.CrossRefGoogle Scholar
Conlon, D., Fox, J. and Sudakov, B. (2013) An improved bound for the stepping-up lemma. Discrete Appl. Math. 161(9) 1191–1196.CrossRefGoogle Scholar
Erdős, P., Hajnal, A. and Rado, R. (1965) Partition relations for cardinal numbers, Acta Math. Acad. Sci. Hungar. 16 93–196.CrossRefGoogle Scholar
Graham, R. L., Rothschild, B. L. and Spencer, J. H. (2013)
Ramsey Theory, Wiley Series in Discrete Mathematics and Optimization. Hoboken, NJ: John Wiley & Sons, Inc., Paperback edition of the second, 1990 edition [MR1044995].Google Scholar
Pudlák, P., Rödl, V. and Sales, M. (2024) On the Ramsey number of daisies I. doi: 10.1017/S0963548324000221.CrossRefGoogle Scholar