Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-11T05:14:11.271Z Has data issue: false hasContentIssue false
  • English
  • Français

On the number of error correcting codes

Part of: Graph theory

Published online by Cambridge University Press:  09 June 2023

Dingding Dong ,
Nitya Mani Open the ORCID record for Nitya Mani [Opens in a new window]  and
Yufei Zhao
Dingding Dong
Affiliation:
Department of Mathematics, Harvard University, Cambridge, MA 02138, USA
Nitya Mani*
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Yufei Zhao
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
Corresponding author: Nitya Mani; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that for a fixed 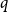$q$, the number of 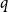$q$-ary 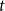$t$-error correcting codes of length $n$ is at most 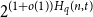$2^{(1 + o(1)) H_q(n,t)}$ for all 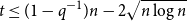$t \leq (1 - q^{-1})n - 2\sqrt{n \log n}$, where 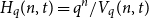$H_q(n, t) = q^n/ V_q(n,t)$ is the Hamming bound and 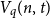$V_q(n,t)$ is the cardinality of the radius 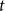$t$ Hamming ball. This proves a conjecture of Balogh, Treglown, and Wagner, who showed the result for 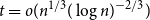$t = o(n^{1/3} (\log n)^{-2/3})$.

Keywords

error correcting codesgraph theorycontainers

MSC classification

Primary: 05C30: Enumeration in graph theory
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 32 , Issue 5 , September 2023 , pp. 819 - 832
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Mani was supported by the NSF Graduate Research Fellowship Program and a Hertz Graduate Fellowship.

Zhao was supported by NSF CAREER award DMS-2044606, a Sloan Research Fellowship, and the MIT Solomon Buchsbaum Fund.

References

Balogh, J., Liu, H. and Sharifzadeh, M. (2017) The number of subsets of integers with no $k$ -term arithmetic progression. Int. Math. Res. Not. IMRN 20 6168–6186.Google Scholar
Balogh, J., Treglown, A. and Wagner, A. Z. (2016) Applications of graph containers in the Boolean lattice. Random Struct. Algorithms 49 845–872.10.1002/rsa.20666CrossRefGoogle Scholar
Delsarte, P. (1973) An algebraic approach to the association schemes of coding theory. Philips Res. Rep. Suppl. 10 vi+97.Google Scholar
Ferber, A., McKinley, G. and Samotij, W. (2020) Supersaturated sparse graphs and hypergraphs. Int. Math. Res. Not. IMRN 2 378–402.CrossRefGoogle Scholar
Kleitman, D. J. and Winston, K. J. (1980) The asymptotic number of lattices. Ann. Discrete Math. 6 243–249.10.1016/S0167-5060(08)70708-8CrossRefGoogle Scholar
Kleitman, D. J. and Winston, K. J. (1982) On the number of graphs without $4$ -cycles. Discrete Math. 41 167–172.CrossRefGoogle Scholar
MacWilliams, F. J. and Sloane, N. J. A. (1977) The Theory of Error-Correcting Codes. North-Holland.Google Scholar
Robert, J. M., Eugene, R. R., Howard, R. Jr. and Lloyd, R. W. (1977) New upper bounds on the rate of a code via the Delsarte-MacWilliams inequalities. IEEE Trans. Inform. Theory 23 157–166.Google Scholar
Samotij, W. (2015) Counting independent sets in graphs. Eur. J. Combin. 48 5–18.10.1016/j.ejc.2015.02.005CrossRefGoogle Scholar
Sapozhenko, A. (2005) Systems of containers and enumeration problems. In International Symposium on Stochastic Algorithms. Springer. 1–13.CrossRefGoogle Scholar
van Lint, J. H. (1975) A survey of perfect codes. Rocky Mountain J. Math. 5 199–224.Google Scholar
van Lint, J. H. (1999) Introduction to Coding Theory. Springer-Verlag, (3rd).Google Scholar