Published online by Cambridge University Press: 25 August 2021
We obtain a polynomial upper bound on the mixing time 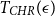 $T_{CHR}(\epsilon)$
of the coordinate Hit-and-Run (CHR) random walk on an
$T_{CHR}(\epsilon)$
of the coordinate Hit-and-Run (CHR) random walk on an 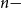 $n-$
dimensional convex body, where
$n-$
dimensional convex body, where 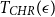 $T_{CHR}(\epsilon)$
is the number of steps needed to reach within
$T_{CHR}(\epsilon)$
is the number of steps needed to reach within  $\epsilon$
of the uniform distribution with respect to the total variation distance, starting from a warm start (i.e., a distribution which has a density with respect to the uniform distribution on the convex body that is bounded above by a constant). Our upper bound is polynomial in n, R and
$\epsilon$
of the uniform distribution with respect to the total variation distance, starting from a warm start (i.e., a distribution which has a density with respect to the uniform distribution on the convex body that is bounded above by a constant). Our upper bound is polynomial in n, R and 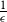 $\frac{1}{\epsilon}$
, where we assume that the convex body contains the unit
$\frac{1}{\epsilon}$
, where we assume that the convex body contains the unit 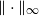 $\Vert\cdot\Vert_\infty$
-unit ball
$\Vert\cdot\Vert_\infty$
-unit ball 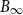 $B_\infty$
and is contained in its R-dilation
$B_\infty$
and is contained in its R-dilation 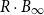 $R\cdot B_\infty$
. Whether CHR has a polynomial mixing time has been an open question.
$R\cdot B_\infty$
. Whether CHR has a polynomial mixing time has been an open question.