Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-25T09:29:24.901Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Erdős–Simonovits–Sós Conjecture about the Anti-Ramsey Number of a Cycle

Published online by Cambridge University Press:  03 December 2003

T Jiang  and
D West
T Jiang*
Affiliation:
Department of Mathematics and Statistics, Miami University, Oxford, OH 45056, USA
D West*
Affiliation:
Department of Mathematics, University of Illinois, Urbana, IL 61801, USA
*
(e-mail: [email protected])
(e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

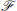Given a positive integer n and a family of graphs, let 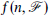denote the maximum number of colours in an edge-colouring of such that no subgraph of belonging to 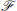has distinct colours on its edges. Erdös, Simonovits and Sós [6] conjectured for fixed k with 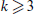that 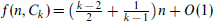. This has been proved for 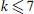. For general k, in this paper we improve the previous bound of 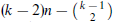to 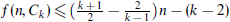. For even k, we further improve it to 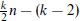. We also prove that 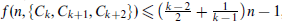, which is sharp.

Type
Research Article
Information
Combinatorics, Probability and Computing , Volume 12 , Issue 5-6: This issue contains volume twelve, parts five and six , November 2003 , pp. 585 - 598
Copyright
Copyright © Cambridge University Press 2003

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research supported by Miami University Faculty Summer Research Grant.

‡

This material is based upon work supported by the NSA under Award No. MDA904-03-1-0037, which requires the disclaimer that any opinions, findings, and conclusions or recommendations expressed in this publication are those of the author(s) and do not necessarily reflect the views of the NSA.