Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-29T16:00:35.478Z Has data issue: false hasContentIssue false
  • English
  • Français

On Iterated Image Size for Point-Symmetric Relations

Published online by Cambridge University Press:  01 January 2008

YAHYA OULD HAMIDOUNE
YAHYA OULD HAMIDOUNE*
Affiliation:
Université Pierre et Marie Curie, Paris, France (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let Γ =(V,E) be a point-symmetric reflexive relation and let υ ∈ V such that |Γ(υ)| is finite (and hence |Γ(x)| is finite for all x, by the transitive action of the group of automorphisms). Let j ∈ℕ be an integer such that Γj(υ)∩ Γ−(υ)={υ}. Our main result states that

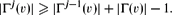
As an application we have |Γj(υ)| ≥ 1+(|Γ(υ)|−1)j. The last result confirms a recent conjecture of Seymour in the case of vertex-symmetric graphs. Also it gives a short proof for the validity of the Caccetta–Häggkvist conjecture for vertex-symmetric graphs and generalizes an additive result of Shepherdson.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 17 , Issue 1 , January 2008 , pp. 61 - 66
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Behzad, M., Chartrand, G. and Wall, C. E. (1970) On minimal regular digraphs with given girth. Fund. Math. 69 227–231.CrossRefGoogle Scholar
[2]Bondy, J. A. (1997) Counting subgraphs: A new approach to the Caccetta–Häggkvist conjecture. In Graphs and Combinatorics (Marseille, 1995). Discrete Math. 165/166 71–80.Google Scholar
[3]Caccetta, L. and Häggkvist, R. (1978) On minimal digraphs with given girth. In Proc. Ninth South-eastern Conference on Combinatorics, Graph Theory, and Computing (Florida Atlantic University, Boca Raton, FL, 1978). Congress. Numer. XXI 181–187.Google Scholar
[4]Hamidoune, Y. O. (1977) Sur les atomes d'un graphe orienté. CR Acad. Sci. Paris A 284 1253–1256.Google Scholar
[5]Hamidoune, Y. O. (1981) Quelques problèmes de connexité dans les graphes orientés. J. Combin. Theory Ser. B 30 1–10.CrossRefGoogle Scholar
[6]Hamidoune, Y. O. (1981) An application of connectivity theory in graphs to factorizations of elements in groups. Europ. J. Combin. 2 349–355.CrossRefGoogle Scholar
[7]Hamidoune, Y. O. (1989) Sur les atomes d'un graphe de Cayley infini. Discrete Math. 73 297–300.CrossRefGoogle Scholar
[8]Hamidoune, Y. O. (1999) On small subset product in a group. In Structure Theory of Set-Addition. Astérisque 258 281–308.Google Scholar
[9]Hamidoune, Y. O., Lladó, A. and Serra, O. (1991) Vosperian and superconnected abelian Cayley digraphs. Graphs Combin. 7 143–152.CrossRefGoogle Scholar
[10]Kemperman, J. H. B. (1956) On complexes in a semigroup. Nederl. Akad. Wetensch. Proc. Ser. A 59 (Indag. Math. 18) 247–254.CrossRefGoogle Scholar
[11]Kemperman, J. H. B. (1960) On small sumsets in an abelian group. Acta Math. 103 63–88.CrossRefGoogle Scholar
[12]Nathanson, M. B. (2006) The Caccetta–Häggkvist conjecture and additive number theory. arXiv:math. CO/0603469.Google Scholar
[13]Seymour, P. Personal communication.Google Scholar
[14]Shepherdson, J. C. (1947) On the addition of elements of a sequence. J. London Math Soc. 22 85–88.CrossRefGoogle Scholar