Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T05:02:37.854Z Has data issue: false hasContentIssue false
  • English
  • Français

The number of maximum primitive sets of integers

Part of: Sequences and sets Multiplicative number theory Combinatorics

Published online by Cambridge University Press:  28 January 2021

Hong Liu ,
Péter Pál Pach  and
Richárd Palincza
Hong Liu
Affiliation:
Mathematics Institute, University of Warwick, Coventry CV4 7AL, UK
Péter Pál Pach*
Affiliation:
MTA-BME Lendület Arithmetic Combinatorics Research Group, Budapest University of Technology and Economics, Magyar tudósok körútja 2, 1117 Budapest, Hungary Department of Computer Science and Information Theory, Budapest University of Technology and Economics, Magyar tudósok körútja 2, 1117 Budapest, Hungary Department of Computer Science and DIMAP, University of Warwick, Coventry CV4 7AL, UK
Richárd Palincza
Affiliation:
MTA-BME Lendület Arithmetic Combinatorics Research Group, Budapest University of Technology and Economics, Magyar tudósok körútja 2, 1117 Budapest, Hungary Department of Computer Science and Information Theory, Budapest University of Technology and Economics, Magyar tudósok körútja 2, 1117 Budapest, Hungary
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A set of integers is primitive if it does not contain an element dividing another. Let f(n) denote the number of maximum-size primitive subsets of {1,…,2n}. We prove that the limit α = limn→∞f(n)1/n exists. Furthermore, we present an algorithm approximating α with (1 + ε) multiplicative error in N(ε) steps, showing in particular that α ≈ 1.318. Our algorithm can be adapted to estimate the number of all primitive sets in {1,…,n} as well.

We address another related problem of Cameron and Erdős. They showed that the number of sets containing pairwise coprime integers in {1,…n} is between 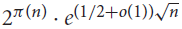${2^{\pi (n)}} \cdot {e^{(1/2 + o(1))\sqrt n }}$ and 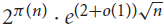${2^{\pi (n)}} \cdot {e^{(2 + o(1))\sqrt n }}$. We show that neither of these bounds is tight: there are in fact 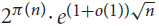${2^{\pi (n)}} \cdot {e^{(1 + o(1))\sqrt n }}$ such sets.

MSC classification

Primary: 11B75: Other combinatorial number theory
Secondary: 11N25: Distribution of integers with specified multiplicative constraints 05A99: None of the above, but in this section
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 5 , September 2021 , pp. 781 - 795
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported partly by the UK Research and Innovation Future Leaders Fellowship MR/S016325/1 and the Leverhulme Trust Early Career Fellowship ECF-2016-523.

‡

Partially supported by the National Research, Development and Innovation Office NKFIH (grant PD115978 and BME NC TKP2020), the Lendület program and the János Bolyai Research Scholarship of the Hungarian Academy of Sciences. He has also received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement 648509). This publication reflects only its author’s view; the European Research Council Executive Agency is not responsible for any use that may be made of the information it contains.

§

Supported by the Lendület program of the Hungarian Academy of Sciences (MTA) and the BME-Artificial Intelligence FIKP grant of EMMI (BME FIKP-MI/SC).

References

Angelo, R. (2018) A Cameron and Erdős conjecture on counting primitive sets. Integers 18 A25.Google Scholar
Balogh, J., Liu, H., Petříčková, S. and Sharifzadeh, M. (2015) The typical structure of maximal triangle-free graphs. Forum Math. Sigma 3 E20.CrossRefGoogle Scholar
Balogh, J., Liu, H., Sharifzadeh, M. and Treglown, A. (2015) The number of maximal sum-free subsets of integers. Proc. Amer. Math. Soc. 143 4713–4721.CrossRefGoogle Scholar
Balogh, J., Liu, H., Sharifzadeh, M. and Treglown, A. (2018) Sharp bound on the number of maximal sum-free subsets of integers. J. Eur. Math. Soc. 20 1885–1911.CrossRefGoogle Scholar
Bishnoi, A. (2017) On a famous pigeonhole problem. Anurag’s Math Blog. https://anuragbishnoi.wordpress.com/2017/11/02/on-a-famous-pigeonhole-problem Google Scholar
Cameron, P. J. and Erdős, P. (1990) On the number of sets of integers with various properties. In Number Theory (Banff, AB, 1988) (Mollin, R. A., ed.), pp. 61–79. De Gruyter.CrossRefGoogle Scholar
OEIS (1999) A051026: Number of primitive subsequences of {1,2,…,n}. The On-line Encyclopedia of Integer Sequences. https://oeis.org/A051026 Google Scholar
OEIS (2003) A084422: Number of subsets of integers 1 through n (including the empty set) containing no pair of integers that share a common factor. The On-line Encyclopedia of Integer Sequences. https://oeis.org/A084422 Google Scholar
OEIS (2010) A174094: Number of ways to choose n positive integers less than or equal to 2n such that none of the n integers divides another. The On-line Encyclopedia of Integer Sequences. https://oeis.org/A174094 Google Scholar
Vijay, S. (2018) On large primitive subsets of {1,2,…,2n}. arXiv:1804.01740Google Scholar