Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-16T17:14:24.675Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Freĭman's Theorem in Vector Spaces

Published online by Cambridge University Press:  01 March 2008

T. SANDERS
T. SANDERS*
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

A famous result of Freĭman describes the sets A, of integers, for which |A+A| ≤ K|A|. In this short note we address the analogous question for subsets of vector spaces over 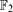. Specifically we show that if A is a subset of a vector space over 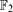with |A+A| ≤ K|A| then A is contained in a coset of size at most 2O(K3/2 log K)|A|, which improves upon the previous best, due to Green and Ruzsa, of 2O(K2)|A|. A simple example shows that the size may need to be at least 2Ω(K)|A|.

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 17 , Issue 2 , March 2008 , pp. 297 - 305
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bourgain, J. (1999) On triples in arithmetic progression. Geom. Funct. Anal. 9 968–984.Google Scholar
[2]Chang, M.-C. (2002) A polynomial bound in Freĭman's theorem. Duke Math. J. 113 399–419.Google Scholar
[3]Deshouillers, J.-M., Hennecart, F. and Plagne, A. (2004) On small sumsets in (ℤ/2ℤ)n. Combinatorica 24 53–68.CrossRefGoogle Scholar
[4]Freĭman, G. A. (1973) Foundations of a Structural Theory of Set Addition, Vol. 37 of Translations of Mathematical Monographs, AMS, Providence, RI. Translated from the Russian.Google Scholar
[5]Green, B. J. and Ruzsa, I. Z. (2006) Sets with small sumset and rectification. Bull. London Math. Soc. 38 43–52.Google Scholar
[6]Green, B. J. and Ruzsa, I. Z. (2007) Freĭman's theorem in an arbitrary abelian group. J. London Math. Soc., 75 163–75.Google Scholar
[7]Rudin, W. (1962) Fourier Analysis on Groups, Vol. 12 of Interscience Tracts in Pure and Applied Mathematics, Wiley–Interscience.Google Scholar
[8]Ruzsa, I. Z. (1994) Generalized arithmetical progressions and sumsets. Acta Math. Hungar. 65 379–388.CrossRefGoogle Scholar
[9]Ruzsa, I. Z. (1999) An analog of Freĭman's theorem in groups. In Structure Theory of Set-Addition. Astérisque 258 323–326.Google Scholar
[10]Sanders, T. Additive structures in sumsets. Preprint. math.NT/0605520. Math. Proc. Cambridge Philos. Soc., to appear.Google Scholar
[11]Tao, T. C. and Vu, V. H. (2006) Additive Combinatorics, Vol. 105 of Cambridge Studies in Advanced Mathematics, Cambridge University Press.CrossRefGoogle Scholar