Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Keevash, Peter
and
Mycroft, Richard
2013.
The Seventh European Conference on Combinatorics, Graph Theory and Applications.
p.
141.
Lih, Ko-Wei
2013.
Handbook of Combinatorial Optimization.
p.
1199.
Lo, Allan
and
Markström, Klas
2015.
$$F$$ F -Factors in Hypergraphs Via Absorption.
Graphs and Combinatorics,
Vol. 31,
Issue. 3,
p.
679.
Keevash, Peter
and
Mycroft, Richard
2015.
A multipartite Hajnal–Szemerédi theorem.
Journal of Combinatorial Theory, Series B,
Vol. 114,
Issue. ,
p.
187.
Martin, Ryan R.
Mycroft, Richard
and
Skokan, Jozef
2017.
An Asymptotic Multipartite Kühn--Osthus Theorem.
SIAM Journal on Discrete Mathematics,
Vol. 31,
Issue. 3,
p.
1498.
Bessy, Stéphane
and
Bousquet, Nicolas
2017.
Colorful paths for 3-chromatic graphs.
Discrete Mathematics,
Vol. 340,
Issue. 5,
p.
1000.
Barber, Ben
Kühn, Daniela
Lo, Allan
Osthus, Deryk
and
Taylor, Amelia
2017.
Clique decompositions of multipartite graphs and completion of Latin squares.
Journal of Combinatorial Theory, Series A,
Vol. 151,
Issue. ,
p.
146.
Martin, Ryan R.
and
Skokan, Jozef
2017.
Asymptotic multipartite version of the Alon–Yuster theorem.
Journal of Combinatorial Theory, Series B,
Vol. 127,
Issue. ,
p.
32.
Hogenson, Kirsten
Martin, Ryan R.
and
Zhao, Yi
2018.
Tiling Tripartite Graphs with 3-Colorable Graphs: The Extreme Case.
Graphs and Combinatorics,
Vol. 34,
Issue. 5,
p.
1049.
Nenadov, Rajko
2019.
Triangle‐factors in pseudorandom graphs.
Bulletin of the London Mathematical Society,
Vol. 51,
Issue. 3,
p.
421.
Lo, Allan
and
Sanhueza-Matamala, Nicolás
2019.
An asymptotic bound for the strong chromatic number.
Combinatorics, Probability and Computing,
Vol. 28,
Issue. 5,
p.
768.
Nenadov, Rajko
Sudakov, Benny
and
Wagner, Adam Zsolt
2020.
Completion and deficiency problems.
Journal of Combinatorial Theory, Series B,
Vol. 145,
Issue. ,
p.
214.
DeBiasio, Louis
Martin, Ryan R.
and
Molla, Theodore
2022.
Powers of Hamiltonian cycles in multipartite graphs.
Discrete Mathematics,
Vol. 345,
Issue. 4,
p.
112747.
Ergemlidze, Beka
and
Molla, Theodore
2022.
Transversal Ck-factors in subgraphs of the balanced blow-up of Ck.
Combinatorics, Probability and Computing,
Vol. 31,
Issue. 6,
p.
1031.
Lang, Richard
and
Sanhueza‐Matamala, Nicolás
2023.
On sufficient conditions for spanning structures in dense graphs.
Proceedings of the London Mathematical Society,
Vol. 127,
Issue. 3,
p.
709.
Cheng, Yangyang
Han, Jie
Wang, Bin
and
Wang, Guanghui
2023.
Rainbow spanning structures in graph and hypergraph systems.
Forum of Mathematics, Sigma,
Vol. 11,
Issue. ,
Han, Jie
Hu, Jie
Ping, Lidan
Wang, Guanghui
Wang, Yi
and
Yang, Donglei
2024.
Spanning trees in graphs without large bipartite holes.
Combinatorics, Probability and Computing,
Vol. 33,
Issue. 3,
p.
270.
Lih, Ko-Wei
2025.
Handbook of Combinatorial Optimization.
p.
1.
Hurley, Eoin
Joos, Felix
and
Lang, Richard
2025.
Sufficient conditions for perfect mixed tilings.
Journal of Combinatorial Theory, Series B,
Vol. 170,
Issue. ,
p.
128.
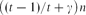 $\bigl ((t-1)/t + \gamma \bigr )n$ vertices of Vj for each j ≠ i, then G contains a perfect Kt-matching, provided n is large enough. Thus, we verify a conjecture of Fischer [6] asymptotically. Furthermore, we consider a generalization to hypergraphs in terms of the codegree.
$\bigl ((t-1)/t + \gamma \bigr )n$ vertices of Vj for each j ≠ i, then G contains a perfect Kt-matching, provided n is large enough. Thus, we verify a conjecture of Fischer [6] asymptotically. Furthermore, we consider a generalization to hypergraphs in terms of the codegree.