Article contents
Monochromatic trees in random tournaments
Published online by Cambridge University Press: 07 November 2019
Abstract
We prove that, with high probability, in every 2-edge-colouring of the random tournament on n vertices there is a monochromatic copy of every oriented tree of order 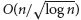 $O(n{\rm{/}}\sqrt {{\rm{log}} \ n} )$. This generalizes a result of the first, third and fourth authors, who proved the same statement for paths, and is tight up to a constant factor.
$O(n{\rm{/}}\sqrt {{\rm{log}} \ n} )$. This generalizes a result of the first, third and fourth authors, who proved the same statement for paths, and is tight up to a constant factor.
MSC classification
- Type
- Paper
- Information
- Copyright
- © Cambridge University Press 2019
Footnotes
Research supported by Dr Max Rössler, the Walter Haefner Foundation and the ETH Zurich Foundation.
Research supported in part by SNSF grant 200021-175573.
References
- 2
- Cited by


