Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T14:19:06.340Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximal Empty Boxes Amidst Random Points

Published online by Cambridge University Press:  14 May 2013

ADRIAN DUMITRESCU  and
MINGHUI JIANG
ADRIAN DUMITRESCU
Affiliation:
Department of Computer Science, University of Wisconsin–Milwaukee, USA (e-mail: [email protected])
MINGHUI JIANG
Affiliation:
Department of Computer Science, Utah State University, Logan, USA (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the expected number of maximal empty axis-parallel boxes amidst n random points in the unit hypercube [0,1]d in 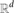$\mathbb{R}^d$ is (1 ± o(1)) 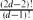$\frac{(2d-2)!}{(d-1)!}$n lnd−1n, if d is fixed. This estimate is relevant to analysis of the performance of exact algorithms for computing the largest empty axis-parallel box amidst n given points in an axis-parallel box R, especially the algorithms that proceed by examining all maximal empty boxes. Our method for bounding the expected number of maximal empty boxes also shows that the expected number of maximal empty orthants determined by n random points in 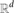$\mathbb{R}^d$ is (1 ± o(1)) lnd−1n, if d is fixed. This estimate is related to the expected number of maximal (or minimal) points amidst random points, and has application to algorithms for coloured orthogonal range counting.

Keywords

Primary 52C45Secondary 68U0568W25
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 22 , Issue 4 , July 2013 , pp. 477 - 498
Copyright
Copyright © Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Aggarwal, A. and Suri, S. (1987) Fast algorithms for computing the largest empty rectangle. In Proc. 3rd Annual Symposium on Computational Geometry, pp. 278–290.Google Scholar
[2]Atallah, M. and Frederickson, G. (1986) A note on finding the maximum empty rectangle. Discrete Appl. Math. 13 87–91.CrossRefGoogle Scholar
[3]Atallah, M. and Kosaraju, S. R. (1989) An efficient algorithm for maxdominance, with applications. Algorithmica 4 221–236.Google Scholar
[4]Augustine, J., Das, S., Maheshwari, A., Nandy, S. C., Roy, S. and Sarvattomananda, S. (2010) Querying for the largest empty geometric object in a desired location. http://arxiv.org/abs/1004.0558v2Google Scholar
[5]Backer, J. and Keil, M. (2009) The bichromatic rectangle problem in high dimensions. In Proc. 21st Canadian Conference on Computational Geometry, pp. 157–160.Google Scholar
[6]Backer, J. and Keil, M. (2010) The mono- and bichromatic empty rectangle and square problems in all dimensions. In Proc. 9th Latin American Symposium on Theoretical Informatics, pp. 14–25.Google Scholar
[7]Bentley, J. L., Kung, H. T., Schkolnick, M. and Thompson, C. D. (1978) On the average number of maxima in a set of vectors and applications. J. Assoc. Comput. Mach. 25 536–543.CrossRefGoogle Scholar
[8]Boissonnat, J.-D., Sharir, M., Tagansky, B. and Yvinec, M. (1998) Voronoi diagrams in higher dimensions under certain polyhedral distance functions. Discrete Comput. Geom. 19 485–519.Google Scholar
[9]Chazelle, B., Drysdale, R. and Lee, D. T. (1986) Computing the largest empty rectangle. SIAM J. Comput. 15 300–315.Google Scholar
[10]Chuan-Chong, C. and Khee-Meng, K. (1996) Principles and Techniques in Combinatorics, World Scientific.Google Scholar
[11]Datta, A. (1992) Efficient algorithms for the largest empty rectangle problem. Inform. Sci. 64 121–141.Google Scholar
[12]Datta, A. and Soundaralakshmi, S. (2000) An efficient algorithm for computing the maximum empty rectangle in three dimensions. Inform. Sci. 128 43–65.Google Scholar
[13]Dumitrescu, A. and Jiang, M. (2013) On the largest empty axis-parallel box amidst n points. Algorithmica, 66 225–248.Google Scholar
[14]Edmonds, J., Gryz, J., Liang, D. and Miller, R. (2003) Mining for empty spaces in large data sets. Theoret. Comput. Sci. 296 435–452.Google Scholar
[15]Giannopoulos, P., Knauer, C., Wahlström, M. and Werner, D. (2011) Hardness of discrepancy computation and ϵ-net verification in high dimension. J. Complexity, to appear.Google Scholar
[16]Kaplan, H., Mozes, S., Nussbaum, Y. and Sharir, M. (2012) Submatrix maximum queries in Monge matrices and Monge partial matrices. and their applications. In Proc. 23rd ACM–SIAM Symposium on Discrete Algorithms, pp. 338–355.Google Scholar
[17]Kaplan, H., Rubin, N., Sharir, M. and Verbin, E. (2008) Efficient colored orthogonal range counting. SIAM J. Comput. 38 982–1011.Google Scholar
[18]Klein, R. (1986) Direct dominance of points. Internat. J. Comput. Math. 19 225–244.Google Scholar
[19]Kudryavtsev, L. D. (2001) The method of undetermined coefficients. In Encyclopaedia of Mathematics (Hazewinkel, M., ed.), Springer.Google Scholar
[20]Kurosh, A. (1975) Higher Algebra, Mir.Google Scholar
[21]Marx, D. (2008) Parameterized complexity and approximation algorithms. Comput. J. 51 60–78.Google Scholar
[22]McKenna, M., O'Rourke, J. and Suri, S. (1985) Finding the largest rectangle in an orthogonal polygon. In Proc. 23rd Annual Allerton Conference on Communication, Control and Computing.Google Scholar
[23]Naamad, A., Lee, D. T. and Hsu, W.-L. (1984) On the maximum empty rectangle problem, Discrete Appl. Math. 8 267–277.Google Scholar
[24]Orlowski, M. (1990) A new algorithm for the largest empty rectangle problem. Algorithmica 5 65–73.Google Scholar