Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T14:10:06.676Z Has data issue: false hasContentIssue false
  • English
  • Français

Lipschitz bijections between boolean functions

Part of: Extremal combinatorics Discrete mathematics in relation to computer science

Published online by Cambridge University Press:  16 November 2020

Tom Johnston  and
Alex Scott
Tom Johnston*
Affiliation:
Mathematical Institute, University of Oxford, OxfordOX2 6GG, UK
Alex Scott
Affiliation:
Mathematical Institute, University of Oxford, OxfordOX2 6GG, UK
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We answer four questions from a recent paper of Rao and Shinkar [17] on Lipschitz bijections between functions from {0, 1}n to {0, 1}. (1) We show that there is no O(1)-bi-Lipschitz bijection from Dictator to XOR such that each output bit depends on O(1) input bits. (2) We give a construction for a mapping from XOR to Majority which has average stretch 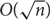$O(\sqrt{n})$ , matching a previously known lower bound. (3) We give a 3-Lipschitz embedding 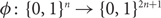$\phi \colon \{0,1\}^n \to \{0,1\}^{2n+1}$ such that 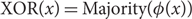$${\rm{XOR }}(x) = {\rm{ Majority }}(\phi (x))$$ for all 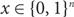$x \in \{0,1\}^n$ . (4) We show that with high probability there is an O(1)-bi-Lipschitz mapping from Dictator to a uniformly random balanced function.

MSC classification

Primary: 68R05: Combinatorics
Secondary: 05D40: Probabilistic methods
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 4 , July 2021 , pp. 513 - 525
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ben-Or, M. and Linial, N. (1989) Collective coin flipping. Adv. Comput. Research 5 91–115.Google Scholar
Benjamini, I., Cohen, G. and Shinkar, I. (2016) Bi-Lipschitz bijection between the boolean cube and the Hamming ball. Israel J. Math. 212 677–703.CrossRefGoogle Scholar
Benjamini, I., Kalai, G. and Schramm, O. (1999) Noise sensitivity of boolean functions and applications to percolation. Publ. Math. Inst. Hautes Études Sci. 90 5–43.CrossRefGoogle Scholar
Bernasconi, A. (1998) Mathematical techniques for the analysis of boolean functions. Bull. Eur. Assoc. Theor. Comput. Sci. 65 228–230.Google Scholar
Boczkowski, L. and Shinkar, I. (2019) On mappings on the hypercube with small average stretch. arXiv:1905.11350Google Scholar
Bollobás, B. (1986) Combinatorics: Set Systems, Hypergraphs, Families of Vectors, and Combinatorial Probability. Cambridge University Press.Google Scholar
Boppana, R. B. (1997) The average sensitivity of bounded-depth circuits. Inform. Process. Lett. 63 257–261.CrossRefGoogle Scholar
Bourgain, J. (2002) On the distribution of the Fourier spectrum of boolean functions. Israel J. Math. 131 269–276.CrossRefGoogle Scholar
Dinur, I. and Safra, S. (2005) On the hardness of approximating minimum vertex cover. Ann. of Math. 162 439–485.CrossRefGoogle Scholar
Erdős, P. and Rényi, A. (1963) On random matrices. Magyar Tud. Akad. Mat. Kutató Int. Közl 8 455–461.Google Scholar
Hastad, J., Leighton, T. and Newman, M. (1987) Reconfiguring a hypercube in the presence of faults. In Proceedings of the Nineteenth Annual ACM Symposium on Theory of Computing (STOC ’87), pp. 274–284. ACM.CrossRefGoogle Scholar
Kahn, J., Kalai, G. and Linial, N. (1988) The Influence of Variables on Boolean Functions. IEEE.CrossRefGoogle Scholar
Kindler, G., Kirshner, N. and O’Donnell, R. (2018) Gaussian noise sensitivity and Fourier tails. Israel J. Math. 225 71–109.CrossRefGoogle Scholar
Lovett, S. and Viola, E. (2011) Bounded-depth circuits cannot sample good codes. In 26th Annual Conference on Computational Complexity (CCC 2011), pp. 243–251. IEEE.CrossRefGoogle Scholar
Mitzenmacher, M. and Upfal, E. (2005) Probability and Computing: Randomized Algorithms and Probabilistic Analysis. Cambridge University Press.CrossRefGoogle Scholar
Mossel, E., O’Donnell, R. and Oleszkiewicz, K. (2010) Noise stability of functions with low influences: invariance and optimality. Ann. of Math. 171 295–341.CrossRefGoogle Scholar
Rao, S. and Shinkar, I. (2018) On Lipschitz bijections between boolean functions. Combin. Probab. Comput. 27 411–426.CrossRefGoogle Scholar