Article contents
Lattice Points of Cut Cones
Published online by Cambridge University Press: 12 September 2008
Abstract
Let ℝ+(ℋn),ℤ(ℋn),ℤ+(ℋn) be, respectively, the cone over ℝ, the lattice and the cone over ℤ, generated by all cuts of the complete graph on n nodes. For i ≥ 0, let 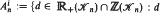 has exactly i realizations in ℤ+(ℋn)}. We show that
has exactly i realizations in ℤ+(ℋn)}. We show that 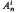 is infinite, except for the undecided case
is infinite, except for the undecided case 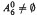 and empty
and empty 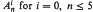 and for i = 0, n ≤ 5 and for i ≥ 2, n ≤ 3. The set
and for i = 0, n ≤ 5 and for i ≥ 2, n ≤ 3. The set 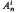 contains 0,1,∞ nonsimplicial points for n ≤ 4, n = 5, n ≥ 6, respectively. On the other hand, there exists a finite number t(n) such that t(n)d ∈ ℤ+(ℋn) for any
contains 0,1,∞ nonsimplicial points for n ≤ 4, n = 5, n ≥ 6, respectively. On the other hand, there exists a finite number t(n) such that t(n)d ∈ ℤ+(ℋn) for any 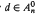 ; we also estimate such scales for classes of points. We construct families of points of
; we also estimate such scales for classes of points. We construct families of points of 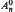 and ℤ+(ℋn), especially on a 0-lifting of a simplicial facet, and points d ∈ ℝ+(ℋn) with di, n = t for 1 ≤ i ≤ n − 1.
and ℤ+(ℋn), especially on a 0-lifting of a simplicial facet, and points d ∈ ℝ+(ℋn) with di, n = t for 1 ≤ i ≤ n − 1.
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1994
References
- 2
- Cited by


