Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-17T15:18:09.245Z Has data issue: false hasContentIssue false
  • English
  • Français

Interval Packing and Covering in the Boolean Lattice

Published online by Cambridge University Press:  12 September 2008

Konrad Engel
Konrad Engel
Affiliation:
Universität Rostock, FB Mathematik, 18051 Rostock, Germany
Get access Rights & Permissions [Opens in a new window]

Abstract

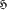Let be the hypergraph whose points are the subsets X of [n] := {1,…,n} with l≤ |X| ≤ u, l < u, and whose edges are intervals in the Boolean lattice of the form I = {C ⊆[n] : X⊆C⊆Y} where |X| = l, |Y| = u, X ⊆ Y.We study the matching number 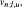i.e. the the maximum number of pairwise disjoint edges, and the covering number 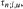i.e. the minimum number of points which cover all edges. We prove that max 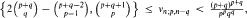and that for every ε > 0 the inequalities 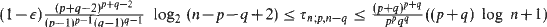hold, where for the lower bounds we suppose that n is not too small. The corresponding fractional numbers can be determined exactly. Moreover, we show by construction that

Type
Research Article
Information
Combinatorics, Probability and Computing , Volume 5 , Issue 4 , December 1996 , pp. 373 - 384
Copyright
Copyright © Cambridge University Press 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bollobás, B. (1965) On generalized graphs. Acta Math. Acad. Sci. Hungar. 16 447–452.CrossRefGoogle Scholar
[2]Bouchemakh, I. and Engel, K. (1992) Interval stability and interval covering property in finite posets. Order 9 163–175.Google Scholar
[3]Bouchemakh, I. and Engel, K. (1994) The order-interval hypergraph of afinite poset and the König property. Discrete Math. (to appear).Google Scholar
[4]Gronau, H.-D. O. F. (1981) Coverings of the complete (di-)graph with n vertices by complete bipartite (di-)graphs with n vertices I. Discrete Math. 37 67–72.CrossRefGoogle Scholar
[5]Kleitman, D. J. (1981) Methods for asymptotic counting. Congressus Numerantium 32 63–85.Google Scholar
[6]Lovász, L. (1975) On the ratio of optimal integral and fractional covers. Discrete Math. 13 383–390.CrossRefGoogle Scholar
[7]Lovász, L. (1977) Flats in matroids and geometric graphs. In: Cameron, P. J. (Ed.), Combinatorial surveys, Proc. 6th British Comb. Conf., Egham 1977, Academic Press, London, 45–86.Google Scholar
[8]Nilli, A. (1994) Perfect hashing and probability. Combinatorics, Probability and Computing 3 1–3.CrossRefGoogle Scholar
[9]Sali, A. (1988) Constructions of ranked posets. Discrete Math. 70 77–83.CrossRefGoogle Scholar
[10]Sperner, E. (1928) Ein Satz über Untermengen einer endlichen Menge. Math. Z. 27 544–548.CrossRefGoogle Scholar
[11]Tuza, Z. (1987) Inequalities for two set systems with prescribed intersections. Graphs and Combinatorics 3 75–80.CrossRefGoogle Scholar
[12]Tuza, Z. (1994) Applications of the set-pair method in extremal hypergraph theory. Bolyai Society Mathematical Studies 3 479–514.Google Scholar
[13]Voigt, B. and Wegener, I. (1988) A remark on minimal polynomials of Boolean functions. In: CSL '88, Proc. 2nd Workshop: Lecture Notes in Computer Science 385, Duisburg, Germany, 372–383.CrossRefGoogle Scholar
[14]Warnke, I. (1994) Personal communication.Google Scholar